指向思维可视化的数学概念教学
2020-06-15葛素儿

【摘 要】指向思维可视化的数学教学是指借助图示、动作、文字、符号等多种数学语言相互转化的视觉学习,将看不见的思维路径显性化,有利于学生的学和教师的教。概念教学中的可视化图示工具可从前结构、单点结构、多点结构和关联结构这四个层级来建构。指向思维可视化的概念教学,可从“原型重现”“初建表象”“表征内化”“结构完善”四方面展开。
【关键词】思维可视化;小学数学;概念教学
思维可视化是指将看不见的思维路径显性化,通常借助图示、动作、文字、符号等来实现。它不仅是一种教学理念,更是一种教学行动,通过引导学生经历“直观地看”“形象地画”“出声地想”等过程,达到思维可视化的目的。
一、思维可视化在概念教学中的作用
数学概念是数学的重要基石,教学中教师要基于学科本质,借助“情境→直观→操作”,引导学生理解数学概念,经历概念形成与同化的过程,把握概念的本质意义。在这一过程中,思维可视化的作用主要体现在以下几方面。
(一)使概念具象化
数学概念教学需要还原生成概念的全过程,即意义建构的过程,但学生在理解概念的过程中往往会出现思维断层的现象。指向思维可视化的概念教学,能帮助学生跨越思维断层,促进概念意义的理解。例如,分数是一个抽象的概念,三年级学生要去理解它并不容易,教学时需要为学生提供直观模型,为学生提供看得见、摸得着的思维支架,把抽象的分数和具体的图像联系起来,促使分数概念具象化,帮助学生理解分数概念。
(二)促知识结构化
借助思维可视化,可以使“点状”的单个概念走向“网状”的概念结构。例如,周长与面积学生容易混淆。教师可以借助对“边长是4分米的正方形,面积与周长相等”的辨析展开教学,引导学生通过在格子图中画一画、列表比一比等可视化操作活动,发现周长与面积的联系和区别,形成较为完善的知识结构。
(三)让经验模型化
“四基”是新一轮教学改革的要求,数学基本活动经验是“四基”的一个维度。思维可视化不仅在数学知识结构化上会产生一定的作用,在数学活动经验模型化上也有着积极的意义。例如在面积的教学中,教师通常会引导学生经历从定性到定量的认识过程,让学生对“度量”的三要素有整体把握,建构起“度量”经验的模型。
二、概念教学中思维可视化的可用工具
曹培英认为,根据可观察的学习结果(SOLO分类评价法),可以将数学理解层次进行梯状刻画,分别是前结构水平、单点结构水平、多点结构水平、关联结构水平和拓展抽象水平。基于数学理解的这五个水平层次,笔者认为概念教学中的可视化图示工具可以从前结构、单点结构、多点结构和关联结构这四个层级来建构,分别表现为实物图、直观模型、表格、韦恩图、思维导图、概念地图、思维树等。
(一)前结构的图示工具,唤醒经验
前结构的图示,基于学生的生活经验,与现实情境紧密结合,通常表现为生活场景或实物图。例如学生在学习周长概念时已经有一些模糊的前概念,已经接触到大量的周长情境,如体育课沿着操场跑一圈、美术课的剪纸、生活中钟面上指针的走动,等等。教学时,教师可采用这些现实情境的动态演示,唤醒学生的生活经验,初步建立“一周表象”。
(二)单点结构的图示工具,聚焦本质
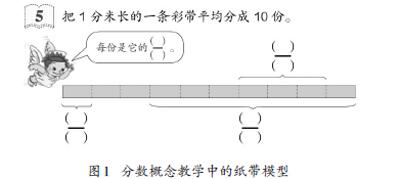
单点结构的图示,指向概念的本质属性。比如,直观模型是分数教学中重要的可视化思维工具,可以是面积模型,也可以采用线段模型、集合模型等。一般来说,这些图示的结构简单,主要聚焦核心要素“平均分”。在认识十分之几的分数时,就可以以这条1分米长的纸带作为学习工具(见图1),从“部分—整体”关系的角度来认识十分之几。
(三)多点结构的图示工具,厘清关系
多点結构的图示,重在沟通知识间的联系,并在知识的生长点上作重点刻画,帮助学生厘清知识之间的内在联系,通常以列表、韦恩图等形式表现。例如在四边形的认识中,教师引导学生对一组图形进行分类,让学生通过比较和分类,归纳并概括出四边形的类型,并聚焦到长方形和正方形的再认识上来,通过列表的可视方法凸现“角”“边”的特征,再用韦恩图表征两者的关系(见表1)。
(四)关联结构的图示工具,建构体系
关联结构的图示,重在表现知识链与思维链纵横交错的结构。思维导图、概念地图、思维树等就属于这一层级的可视化工具。例如在概念教学中,教师可用节点表示概念,连线表示概念之间的关系,通过提纲式、辐射式、发散式等不同思维路径反映概念之间的层级关系,建构知识体系。
三、指向思维可视化的概念教学结构
指向思维可视化的概念教学,可经历“原型重现→初建表象→表征内化→结构完善”的过程,达到概念建构的目的。
(一)“原型”搭桥,对接生活经验
概念教学的起始阶段,思维可视作用主要体现在与生活经验对接上,以“直观地看”为主要活动形式。一般在课堂上,教师会采用前结构的图示,即用生活中的原型来引入。现实生活中的原型(前概念)是理解概念不可或缺的学习素材。例如,分数的原型之一是“平均分物”,教学中用“分蛋糕”作原型,经历以下学习过程。
1.出示情境图,唤醒生活经验:4个蛋糕平均分给2个人,每个人分到几个?2个蛋糕呢?1个蛋糕呢?你能用合适的数分别表示平均分的结果吗?
2.动态直观演示,初步感悟分数:结合对1个蛋糕平均分的动画演示,理解“半个→[12]个”“[13]个”“[14]个”是多大。
在这里,教师像引入自然数一样引入分数,借助平均分的生活原型,唤醒学生的生活经验。为让学生初步认识分数,积累等分经验,教师引导学生参与创造[12],利用[12]个、[13]个、[14]个的实物模型,让学生知道分数的意义,在具体“平均分”的可视化情境中初步建立分数概念。
(二)“表象”支撑,对接心理图示
在初识概念后,概念会以一定的表象在学生的头脑中编码储存,从而产生心理图示。这时候,教师就要提供呈单点结构或多点结构的可视化图示,引导学生经历“直观地想”“形象地画”等可视化学习过程,促成概念表象的具象化。例如“1厘米”表象的建立,教师就可借助尺子这一可视化学习工具,采用以下几个步骤组织教学。
1.尺子上的1厘米:这把尺子中隐藏着许多1厘米,请你在尺子上找一个你心中的1厘米。
2.生活中的1厘米:哪些物体的长度或厚度大约是1厘米?
3.头脑中的1厘米:闭眼想象、用手比画1厘米有多长,再徒手画一画。
通过找、想、比、画等可视化的方式,物化学生头脑中的1厘米,转化成学生可触摸的指甲长度、书本厚度等生活参照物,化抽象为具体,帮助学生建立起1厘米的表象。
(三)“表征”操作,对接概念内涵
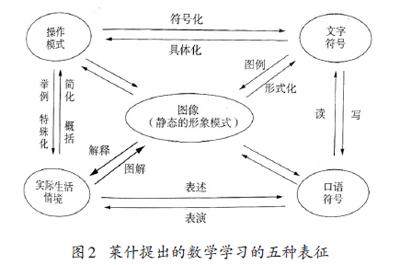
莱什提出数学学习的五种表征(见图2),分别为实际生活情境、图像、操作模式、口语符号和文字符号。当学生对概念表象具象化时,教学应借助这五种表征活动让概念表象操作化与活动化,实现多种表征之间的沟通互译,促进概念的深化理解,这是概念教学精致化的过程。
例如认识几分之几的教学,学生虽然有几分之一的概念,但认知经验和活动经验还显得比较单薄,教学中依然需要通过折一折、画一画、说一说、辩一辩等多元表征活动,让学生借助四等分的正方形创造四分之几,在动手操作中感受四分之几的含义。活动后,组织学生汇报,并针对学生可能出现的情况,教师追问梳理,分4个层次。
追问1:这些分数里面各有几个[14]?
学生对于[44的]理解可能会有困难,教师可以结合图示以及其与[14]的联系来让学生理解[44]。
追问2:为什么涂色部分的形状不一样,却都可以用[34]来表示?
追问3:你知道下面图形中涂色部分是整个图形的[□□]吗?(长方形、圆、三角形、线段)
追问4:在下面的巧克力图中,你能找到哪些分数(平均分成2份;平均分成4份;平均分成8份)?与同桌一起找一找,并说一说每个分数表示什么。
在这一过程中,教学所采用的图示思维工具一般是多点结构的,教学经历动手操作、画图说明、语言表达、生活拓展等思维活动,与分数建立互译沟通,帮助学生理解分数概念。
(四)“结构”完善,对接概念体系
在概念深化理解的过程中,需要对学生的认知结构进行改組与扩充,形成概念网。例如学完“比”后,需要对“除法”“分数”“比”这三者之间的关系进行梳理,可通过列表(见表2)厘清概念之间的内在联系与区别,完善认知结构。
综上所述,利用可视化工具,让学生在概念的产生、形成、理解、深化的过程中,实现概念的意义建构、概念体系的建构。
指向思维可视化的概念教学意味着教学研究的视角亦要革新。在课前,教师需要深度解读概念的本质,明了思维可视化在本课教学的落脚点;需要深度理解学生,把握学生的前概念水平;需要深度解读教材,明晰可视化思维的支架有哪些及如何用好这些支架;需要深度设计教学,把握指向思维可视化的教学路径。
参考文献:
[1]蒋碧云.基于“数学理解层次”的教学路径探索——思维可视化的另一种打开方式[J].上海教育科研,2019(22):68-71.
[2]葛素儿.思维可视,情理相融——第一学段数学教学中图式思维活动的设计与运用[J].教学月刊·小学版(数学),2015(10):40-42.
[3]尹晗,张际平.思维可视化视角下的未来课堂架构研究[J].远程教育杂志,2016(2):106-112.
[4]席爱勇.数学多元表征:让概念形成过程“看得见”[J].教育研究与评论(小学教育教学版),2017(9):65-67.
(浙江省杭州市富阳区富春第二小学 311400)
