“小数的初步认识”教学中十进分数的介入方式
2020-06-15赵胜华徐军红
赵胜华 徐军红
【摘 要】基于思维可视化教学理念,“小数的初步认识”的教学,可以通过激活十进分数以“符号操作”的方式介入小数意义建构,使小数的“十分”与“十进”的动态过程在头脑中可视化,从而使学生的思维从静态走向动态、从复杂走向简洁,立体建构小数的意义。
【关键词】小数;思维可视;教学
思维可视化教学是指通过一定的教学策略,帮助学生理解知识的产生和形成过程,使思维变得“看得见”、可琢磨。基于思维可视化教学理念,我们重构教学如下。
一、画图表征,具象解惑
学生是带着自己对小数的了解来到课堂的,且各有差异。实践中我们采用了特级教师袁晓萍设计的材料,在操作上做了新尝试。
【教学片段1】
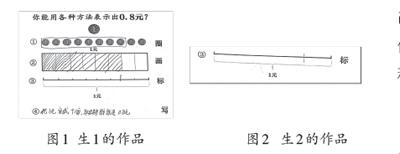
师:你能选择合适的图形来表示你对0.8元的理解吗?
教师提供学习单,学生独立尝试解决,小组交流。之后全班讨论,逐一呈现错例,学生说明想法,再纠正完善。
生:我不同意生1的想法(如图1),他只画了6格,不能表示0.8元。
生:要平均分成十等份,再取其中的8份,他分错了。
生:我心里想的是十等份,画错了。
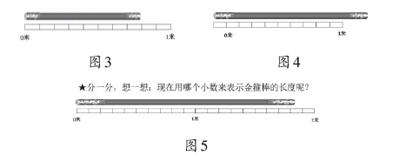
师:感谢你的失误带给我们思考。我们再来看生2的创作(如图2)。你来猜猜看,他是不是很任性地点上了这一点?
生:不是的,他这里有看不见的十等分。
生:还有看不见的8等分和2等分。
(师生合作完善等分方法)
师:为什么十等分呢?
生:1元里有10个1角,把1元平均分成10份,每一份是1角,也就是0.1元,8份是8角,也就是0.8元。
(引導学生规范语言表征:把1元平均分成10份,取8份,就是0.8元)
【设计意图】
1.小数的产生源于计量的需要。张奠宙先生认为,小数的出现是基于十进制表示数量的需要。史宁中先生认为建立小数的概念,一方面是为了现实世界中数量表达的需要;另一方面是为了数学本身的需要,主要是为了表示无理数,即小数的范围要比分数的范围广。
有限小数是一种特殊的分数(十进分数),理解小数的核心在于重新理解十进制,即理解“十分”与“十进”。教学中要引导学生初步感受到:小数并不是十进分数改写产生的,而是特殊平均分(十分)的结果,是自然数的十进位置值从高位往低位扩展的结果。
2.画图表征使经验可视化。画图表征能帮助学生在客观问题与主观心智表达之间建立起一座桥梁,能充分暴露学生的已有经验,使学生经验可视。学生在“画图—读图—用图”的过程中,明白自己已经知道了什么,还存在怎样的困惑,并借助错例纠正归纳共同点,“逼”学生将10的幂次方等分和合的过程“说清楚”,将内隐的思维可视化。
二、符号表征,改造经验
借助一定的视觉表征形式,可使抽象的概念具象化,有利于学生获得对知识本质的直观、简洁、清晰的理解。但不可忽视的是,表征之间的转化是学习的关键环节,转换能力不佳会影响数学学习。激活十进分数的“过程”可实现图和文之间的心理转换。
【教学片段2】
师:(逐一展示正例)这些表示方法有什么共同点?
生:都是十等分取8份。
师:如果用一个分数表示这些图的共同特点,你会用哪个分数?
生:[810]。
师:从[810]你看到怎样的分和取?
生:都是把1元十等分,取8份。
师:8角和0.8元之间用哪个数学符号来连接?(等号)那[810]应该放在哪个位置呢?8角和0.8元都带有一个单位,想一想,[810]带上怎样一个单位比较合适?
生:我认为应该和0.8元在一起,因为都是先把1元平均分成10份,再取了8份。
生:[810]是把1元看作单位的,应带上的单位是“元”。
生:这三个数的大小是一样的。
在互动中,移动纸卡片,建立等式 8角=[810]元=0.8元。
师:[310]元,你想到什么?
【设计意图】
1.英国沃瑞克大学的韬尔提出:数概念是一个典型的过程性概念,既是过程又是概念。学生建构数概念需要在具体操作的基础上,通过压缩和内化,逐步形成为对象的概念,并纳入已有的认知结构。
分数概念和小数概念的建构都依据这样的步骤展开,但两者在建构过程中又有所区别,如分数初步认识时,学生鲜明感受的是“过程”,而小数初步认识时,由于已有的生活学习经验,学生鲜明感受的反而是“对象”。因此,如何将两者合理联合是小数意义建构的关键。
2.十进分数以“符号操作”介入意义建构。像人民币、面积模型、米制系统、数轴等直观、半直观模型的核心是“十分、十进”,从具体操作压缩内化到对象,需要载体。谁能成为多功能载体呢?根据布鲁纳“三种操作”的认知理论,表象操作是实物操作到符号操作的桥梁,而十进分数这一富有“过程性”的数学语言恰能成为从符号操作到思维操作的桥梁。
教师以“如果用一个分数表示这位同学的想法,你会用哪个分数”引导学生用十进分数抽象过程,从而使分与合的动态过程可视化。然后以“[810]应该放在哪个位置呢”为驱动,借助纸卡片的移动自然地建构“8角=[810]元=0.8元”,既使学生感受到三者的相等关系,更使学生的思维从静态走向动态,最后逆向思考“[310]元,你想到什么”。在互译中,借助“数”(shǔ),初步体验“十分”“十进”的思维过程。十进分数与小数的关系不仅限于对应关系,我们更应把它作为数学语言,成为学生思维和交流的载体。
三、动态表征,形成系统
当学生初步完成某一概念的建构后,教师可以在动态变化的情境中让学生用所学的概念进行判断,完善概念的建构。
【教学片段3】
师:孙悟空的金箍棒很神奇。你能根据下图,用小数表示金箍棒每次变化后的长度吗?
(1)学生根据金箍棒长短变化,口答小数(0.2米,0.8米,0.1米)。(图3)
(2)(金箍棒快速伸长,产生新情况)你知道现在是几米?(估:1~2米之间,接近1米);显示5等分,引发学生对1.1米与1.2米的争论(隐藏的十等分);继续数1.4米,1.6米……2米。(图4)
(3)(新冲突:1.82米)想用一个数准确表示现在金箍棒的长度,你会吗?(图5)
(4)课堂总结,梳理沟通。
【设计意图】
什么样的材料能实现米制系统的抽象过渡呢?“金箍棒”无疑是一个“有趣”的好材料。“金箍棒”在变长变短的动态表征中凸显小数的“十分”,巧妙、无痕地发展了学生的数感,认识比1大的多位小数。
通过追问引导学生回顾学习历程,从源头再认识小数的意义,帮助学生将新概念纳入自己的知识结构。
基于思维可视,激活十进分数以“符号操作”的方式介入小数意义建构,即借助十进分数这一数学语言,使小数的“十分”与“十进”的动态过程在头脑中可视化,从而使学生的思维从静态走向动态、从复杂走向简洁,立体建构小数的意义。
参考文献:
[1] 袁晓萍.学会向学生借智慧[M].杭州:浙江教育出版社,2018(11):244-256.
[2] 史宁中.基本概念与运算法则[M].北京:高等教育出版社,2016(1):16-19.
[3] 张奠宙.小学数学研究[M]. 北京:高等教育出版社,2009(1):89-94.
[4] 鲍建生.数学学习的心理基础与过程[M]. 上海:上海教育出版社,2014(4):236-239.
[5] 蒋碧云.基于“数学理解层次”的教学路径探索——思维可视化的另一种打开方式[J].上海教育科研,2019(22):68-71.
(浙江省杭州市富阳区永兴小学 311400
浙江省杭州市富阳区湖源乡中心小学 311400)
