基于禁忌搜索算法的废弃家具回收车辆路径优化

庞 燕，罗华丽，夏扬坤

(中南林业科技大学 物流与交通学院，湖南 长沙 410004)

0 引言

随着人们生活水平的提高，消费观念发生了很大的改变，对新奇和时尚家具的追求也越来越高，家具产品的更新换代速度逐年加剧。另外，我国中小家具制造企业众多，企业为了迎合消费者需求，抢占市场份额，大肆推陈出新，这种粗糙的生产模式造成家具产能过剩，导致大量家具因滞销而废弃于仓库之中[1]，既浪费了社会资源又污染了环境。可见，废弃家具的回收处理已经成为一项亟需解决的社会难题。根据生产者责任延伸制度[2]，家具制造企业必须承担回收废弃家具的责任[3]。对废弃家具进行回收处理再利用，不仅能够有效缓解企业面临的环保压力，树立企业的良好社会形象，还能创收一定的经济效益[4]。

废旧家具回收属于逆向物流的范畴，从物品特点来看，其一般体积和重量较大且形状不一，在装载上需要对车辆容量进行限制。从回收的特殊性来看，回收需求点客户分散于各个小区，对路线规划要求高，而企业可以自由选择回收服务时间。车辆路径问题(Vehicle Routing Problem, VRP)是废弃家具回收逆向物流体系中的核心环节，对废弃家具回收车辆路径问题(Vehicle Routing Problem of Waste Furniture Recycling, VRPWFR)进行研究具有较高的实践价值，缩短行驶距离和减少使用车辆数可以在较大程度上降低企业的总成本。在对各回收站点的废弃家具进行配载装车时，需要结合各站点的需求量和地理位置分布情况，根据车辆装载能力限制划分车辆路径，既要遍历所有站点，还要尽可能地缩短行驶距离并减少车辆数，从而形成一个带容量约束的双目标函数家具回收VRP。

带容量约束的车辆路径优化问题(Capacitated Vehicle Routing Problem, CVRP)在物流配送领域中应用广泛，对CVRP进行有效改进能够在较大程度上降低物流成本、提升效益和客户满意度。因为CVRP是NP-hard问题，一般的精确算法[5]很难求解大规模配送问题，而经典的启发式算法又不具备全局寻优能力，所以设计智能启发式算法(智能优化算法)进行求解。曹高立等[6]设计了一种混合量子进化算法求解CVRP，利用二维量子位观测模型直接产生十进制编码个体，增强了算法邻域搜索的能力；李阳等[7]在生物共栖算法的基础上，结合变邻域搜索策略，采用混合智能启发式搜索算法求解CVRP。

部分学者采用两阶段的方式来降低求解难度，提高了算法效率。Mohammed等[8]提出两阶段遗传算法，在找到车辆行驶最短路径的基础上寻找带容量限制的车辆路径；Lai等[9]在求解具有时间窗的VRP时，第一阶段采用模拟退火算法减少路径中的车辆数，第二阶段采用禁忌搜索算法(Tabu Search Algorithm, TSA)降低总行驶成本，结果表明两阶段求解方式能够更快地获得优化解；Wang等[10]在处理带时间窗的多目标多中心的VRP时，设计了一个两阶段多目标进化算法，第一阶段寻找极值解，第二阶段以极值解为基础进行扩展寻找最优解，实验结果表明两阶段求解方式确实有利于解的改进；李阳等[7]在求解带模糊需求的容量限制VRP时，设计了两阶段变邻域TSA，第一阶段处理客户的模糊需求，第二阶段处理客户的实际需求，最后通过算例测试验证了两阶段求解方式是解决CVRP的有效途径。

TSA是对局部搜索算法的扩展，是一种模仿人类智能思维的全局逐步寻优智能启发式算法，很多学者对TSA表现出了浓厚的兴趣。Wang等[11]基于解决方案的禁忌策略，采用协调的哈希函数加速禁忌状态，产生了更好的优化方案；Ben等[11]针对背包问题设计了一个多邻域概率搜索TSA；Tao等[12]研究了三维装箱约束VRP，利用迭代禁忌搜索寻找可行路径；Liu等[13-15]对TSA进行了重点研究，指出TSA具有简单性、适应性和易操作性等优点。由以上文献可以看出，在TSA中，邻域结构可以增强算法的搜索能力，禁忌表可以通过避免算法较早陷入局部最优来增强寻优能力，对CVRP求解起到了很好的优化作用。随着优化模型的不断拓展，其求解变得越来越复杂，本文设计的改进两阶段禁忌搜索算法(Improved Two-stage Tabu Search Algorithm, ITTSA)也将围绕邻域结构和禁忌表两个方面进行改进。

1 问题描述与数学模型的构建

1.1 问题描述

本文所研究的VRPWFR是在满足回收站点需求量di和车辆装载能力限制Q的基础上，对废弃家具回收车辆路径进行规划，从而合理地安排车辆k在各回收站点i之间的行驶顺序，并最小化总行驶距离和车辆数。

在每次回收中需要满足的条件为：①路径中仅有一个废弃家具处理中心，但拥有多个家具回收站点(客户点)；②各回收站点的地理位置和回收量已知；③处理中心的地理位置已知；④处理中心拥有足够数目的同车型车辆；⑤每个回收站点只能被车辆拜访一次；⑥全部车辆从处理中心出发，回收废弃家具后需返回原处理中心；⑦车辆在各点之间的行驶距离符合三角不等式约束。

1.2 相关符号定义

为了方便问题描述，定义相关符号如表1所示。

表1 相关符号的含义说明

1.3 数学模型构建

(1)

minK。

(2)

s.t.

(3)

(4)

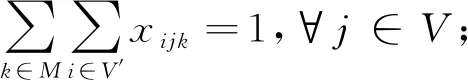
(5)

(6)

(7)

(8)

K≥Kmin=；

(9)

xijk∈{0,1}∀i,j∈V′,∀k∈M。

(10)

其中：目标函数式(1)表示最小化路径的总距离值；目标函数式(2)表示最小化使用车辆数；式(3)表示回收车辆的容量约束，保证每辆车不会超过其载重；式(4)保证到达回收站点i的车辆数与离开该站点的车辆数一致；式(5)保证到达每个回收站点的车辆有且仅有一辆车；式(6)可消除子回路；式(7)和式(8)保证全部车辆从回收处理中心出发并最终返回原出发点；式(9)用于估算所需的最少车辆数；式(10)表示车辆k是否从回收点i到点j(i≠j)，是则为1，否则为0。

2 禁忌搜索算法设计

TSA是一种具有指导性搜索能力的智能优化算法，其可以利用短期禁忌表来记忆相应的禁忌信息，避免搜索重复解。以往的TSA将同一邻域交换点对作为禁忌对象，存在禁忌重复的弊端，本文设计一个新的线性禁忌表，将邻域算子和邻域交换点对同时作为禁忌对象，并设计多邻域结构来模拟相应局部极值的分布情况。具体算法设计见后续说明。

2.1 两阶段求解方式的设计

作为旅行商问题(Traveling Salesman Problem, TSP)的一种拓展，VRPWFR已被证明是NP-Hard问题，其在求解较大规模精确解上具有极高的难度。结合以往VRP研究[8]经验可知，两阶段求解方式有助于降低求解难度，提升求解效率。本文将两阶段求解思想融入TSA，第一阶段，根据所有客户回收站点的位置编号生成TSP路径；第二阶段，根据TSP路径排列中站点的需求量和车辆装载能力限制划分VRP路径，尽可能地使车辆满载(此举对应了第二目标最小化使用车辆数K)。

2.2 解的评价设计

在每次迭代生成候选解集后，都先挑选出当前的全局最好解Sbest和当前解Snow。其中，Sbest用于存储迭代中出现的最好结果，Snow用于在下一次迭代的邻域变换过程中生成候选解集。本文采用总行驶距离值Z来评价解的优劣。在候选解无禁忌的情况下，认为Z值越小其解越优。在每次迭代生成候选解集后，如果最佳候选解Sbestca比全局最好解Sbest更优，则不考虑禁忌情况，直接将Sbestca设定为全局最好解Sbest和当前解Snow；若Sbestca比Sbest更差，则将非禁忌的最佳候选解*Sbestca设定为当前解Snow。

2.3 解的表示与初始解的生成

问题的一个解可以用回收处理中心点0和各个站点的编号排列来表示，每一个解都有其对应的TSP路径和VRP路径。在其TSP路径中，起始点和终止点为点0，中间节点为各站点的自然数编号。在其VRP路径中，数字0是不同VRP路径划分的分界点。例如，在VRP路径S=(0-2-4-1-0-8-6-5-0-9-7-12-0-…-0)中，前3条车辆路径分别为(0-2-4-1-0)，(0-8-6-5-0)，(0-9-7-12-0)。本文采用随机方式生成可行初始解。初始解的具体生成过程如下：①随机生成一个关于站点编号的自然数TSP排列，并构建TSP路径；②根据该TSP路径、站点回收量和车辆装载能力限制划分相应的闭合式VRP路径(尽可能地使车辆满载)。

2.4 邻域结构设计

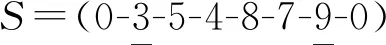
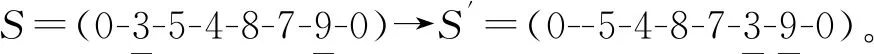
(3)分序点插入 分两种情形：

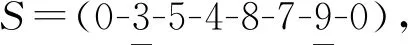
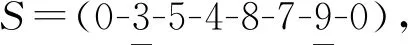
2.5 线性禁忌表设计

在算法中引入短期线性禁忌表，记录已经搜索过的当前解所对应的禁忌对象，在后续一定搜索次数中，不再对该禁忌对象进行重复搜索，以提升算法跳出局部最优的能力。禁忌表用来储存禁忌对象，本文设计一个大小为16×3的线性禁忌表，将邻域算子和邻域交换点对都作为禁忌对象，采用先进先出机制，当禁忌信息溢出时，释放排在最前面的禁忌信息。

TSA禁忌的目的是为了避免重复搜索相同解，若为直接禁忌解，则匹配计算量会很大，在以往的TSA[16-17]中，一般用禁忌邻域交换点对对象模拟相应候选解的禁忌情况。然而，同一邻域交换点对可能对应多个不同的候选解，容易造成对优良候选解的过度禁忌。因此，本文对禁忌表进行改进，将邻域算子编号也加入禁忌表，使得禁忌对象改变为“邻域算子编号邻域交换点1邻域交换点2”，在迭代搜索中，只有当邻域算子编号和邻域交换点在禁忌表中同时存在时，才认为其对应的候选解是禁忌的，从而扩大了搜索范围，避免陷入早熟。另外，对候选解的禁忌情况进行标记，可以更准确地模拟相应候选解的禁忌，降低搜索的重复程度，缩短搜索时间，提升算法邻域搜索的效率，有利于优化候选解的质量。

2.6 终止条件

终止条件包括邻域搜索的终止条件和迭代的终止条件。邻域搜索的终止条件有一个，即每次迭代中候选解的数目达到预设的上限值N0；迭代的终止条件有两个，达到其中任意一个便可终止迭代：①总的迭代次数达到预设的上限值N1；②全局最好解连续保持不变的迭代次数达到预设的上限值N2。为了使算法能够适用于求解不同规模问题，将N0，N1，N2均设置为与回收站点有关的线性函数，取N0=50+N，N1=6 000+150N，N2=5 000+30N。

2.7 算法流程图

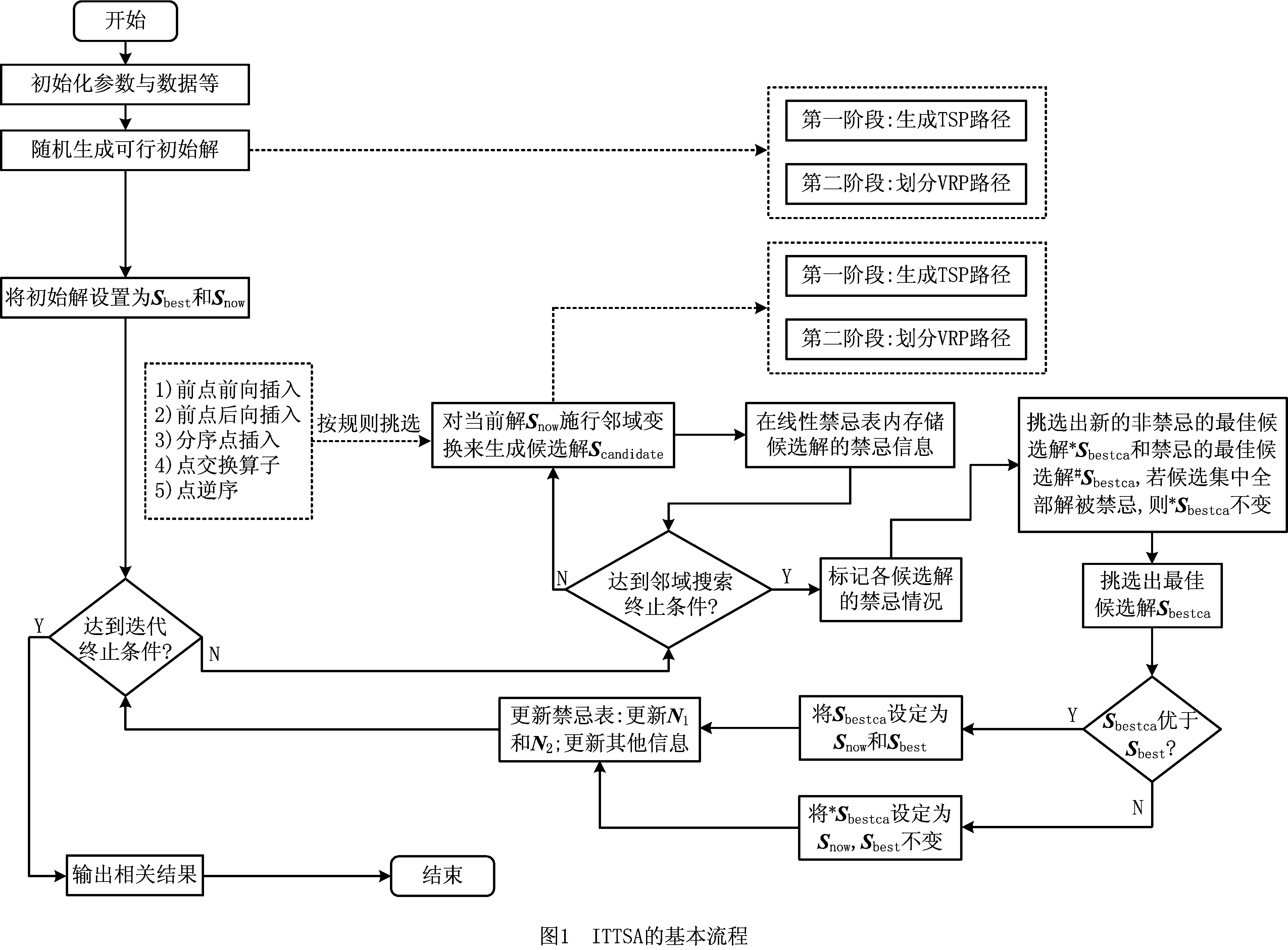
本文ITTSA的基本流程如图1所示。

3 算法测试与分析

Aleman等[18]在求解带装载能力限制的VRP时，设计了构造启发式算法(Constructive heuristic Approach, CA)、迭代构造算法(Iterative Constructive Approach, ICA)和迭代构造变邻域下降法(Iterative Constructive Approach plus Variable Neighborhood Descent, ICA+VND)(ICA+VND采用两阶段求解方式，以ICA的结果作为VND的初始解)，并对站点规模分别为50/75/100的C1/C2/C33个算例进行了测试分析，具体请参考文献[18]。为了方便对比分析，本文也选用C1，C2，C33个算例进行测试分析。本文采用MATLAB2014a进行编程，在荣耀Magic Book、CPU为i5-8250U、主频为1.60 GHz、内存为8 GB的电脑上完成计算，对每个算例独立测试20次。

3.1 邻域结构测试

不同邻域结构[19]对应不同的算法搜索空间，当邻域过多时，算法运行成本过大，因此对邻域组合进行测试来确定最优邻域结构，以减少不必要的搜索，从而提高算法寻优能力和运行速度。本文设计了5种邻域算子，为了比较各邻域算子的寻优性能，探讨邻域结构的优化能力，以C1算例分别对5种邻域算子的不同组合情况进行测试，每一种情况测试20次，并对求解结果进行统计分析。

(1)采用1种邻域算子

表2所示为各邻域算子的总距离Z值的最好值Zbest、平均值Zavg、最差值Zworst、极差值Zdev(最差值与最好值的差值)、极差百分比Zdev/%(极差值相对于最好值的百分比)、标准差Zsd及求得的平均车辆数Kavg，其中Zbest，Zavg，Zworst，Kavg体现了算法的寻优能力，Zdev，Zdev/%，Zsd体现了算法求解的稳定性。表2中NO-1/NO-2/NO-3/NO-4/NO-5分别表示所采用的邻域算子1/2/3/4/5，加粗数据表示比较数据中的最好值。从表2可见，对于同一算例的数据，NO-5的各项参数值均为最小，相对于NO-5而言，NO-1，NO-2，NO-3，NO-4求得的最短距离值较高，偏差百分比较大，标准差较大，稳定性较差。由此可见，NO-5的优化效果和稳定性最好。选取Zbest，Zavg，Zworst的数据绘制优化结果，如图2所示。

表2 采取1种算子测试的总距离值Z的比较

(2)采用2种邻域算子

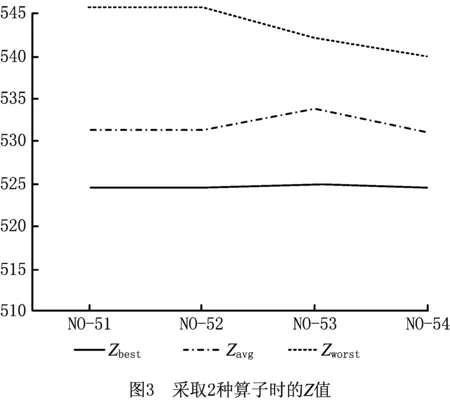
因为采取1种邻域算子进行测算得到的结果中NO-5更优，所以在两种邻域算子进行测算时将NO-5与其他算子进行组合，共4种情况，用同一算例进行测算，分析结果如表3所示。从最好值、平均值、最差值和标准差等结果来看，NO-51和NO-52的结果一样，由此可见，NO-1(前点前向插入算子)或NO-2(前点后向插入算子)的移动方式相似，产生的效果也一样；NO-54的优化结果最好，稳定性最强，车辆数也达到了最小车辆数的要求。绘制优化结果，如图3所示，其中NO-51表示在算例测试中采取邻域算子5和邻域算子1的组合。

表3 采取2种算子测试的总距离值Z的比较

(3)采用3种邻域算子

根据采取两种邻域算子的数据结果，在采取3种邻域算子计算时，将NO-5，NO-4与其他算子进行组合，共有3种情况，用同一算例进行测试，分析结果如表4所示。从平均值来看，NO-541比其他两种组合情况稍优，但是在找到最好值时，NO-542的值更接近最优；从标准差来看，NO-542算出的值最低，说明波动较小，稳定性最好；3种邻域算子组合的车辆数都已降至最低。因为算法的第一优化目标是求得最短距离，所以综合来看，NO-542的组合情况最优。将各组合算子的优化结果绘制成曲线图，如图4所示。

表4 采取3种算子测试的总距离值Z的比较

(4)采用4种邻域算子

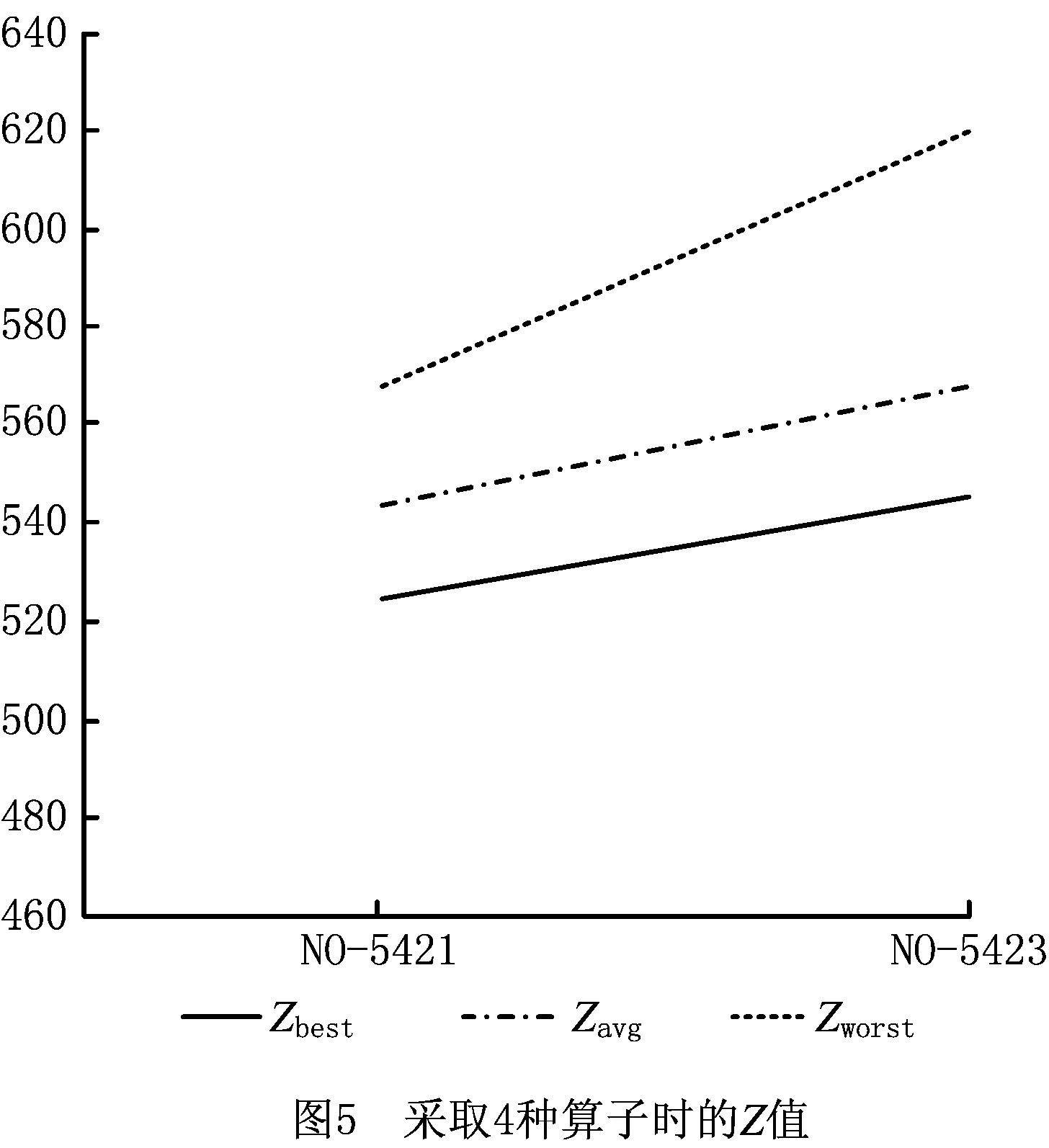
根据采取3种邻域算子的数据分析结果，在进行4种邻域算子计算时，将NO-5，NO-4，NO-2与其他两种算子进行组合，共有两种情况，以同一算例进行测算，数据分析结果如表5所示。从各项数据来看，NO-5421明显优于NO-5423，如图5所示。

表5 采取4种算子测试的总距离值Z的比较

(5)采用5种邻域算子

对5种邻域算子进行测试，在NO-5421的基础上以同一算例对5种算子组合进行测试，数据分析结果如表6所示。

表6 采取5种算子测试的总距离值Z的比较

综合以上5种测试结果，将每种算子测试时的最好结果统一起来进行比较，如表7和图6所示。当分别使用1/2/3/4/5个邻域算子进行测算时，取得最好优化能力的是NO-5,NO-54,NO-542,NO-5421，NO-54213。在这5种最佳组合中，其优化能力大小排序是NO-54>NO-542>NO-54213>NO-5>NO-5421。

表7 各最优算子测试的Z值比较

分析原因，在对单个算子进行测算时，NO-5相比其他4个算子体现了很好的优化效果，说明点逆序算子的寻优能力和稳定性是5个算子中最好的，其在NO-54组合中也发挥了较好的作用。然而，NO-54的Zavg比NO-542稍弱，相差0.25，这是因为NO-4(点交换算子)的操作是将随机挑选的两个点进行交换，解空间变换较小，搜索范围较小，所以搜索的候选解集较差。相比之下，NO-2(前点后向插入算子)在进行邻域变换时，其解空间有所扩大，算法搜索空间增大，从而提高了候选解的质量，但是因为NO542邻域结构的算子更多，运算过程更长，所以稳定性不如NO-54。

综合来看，NO-54的优化效果具有较大优势，其能求得最短行驶距离，且车辆数最小，稳定性较好，在求解质量和效率上优于其他邻域结构。因此，使用2种邻域算子的结果明显更优，即点逆序算子和点交换算子组成邻域结构使算法的优化效果更好。

3.2 文献对比分析

结合3.1节中的邻域算子组合测试结果可知，采用NO-54的优化效果最好。因此，本文ITTSA在求解C1，C2，C33个算例时，直接采用NO-54构建成的多邻域结构体进行测试和对比分析。

表8所示为Z的最好值Zbest、平均值Zavg、最差值Zworst、极差值Zdev、极差百分比Zdev/%和标准差Zsd。可见全部算例的Z值偏差百分比控制在5%以下，均值偏差为3.87%，平均标准差为8.91。根据以往大规模配送VRP的研究可知，本文ITTSA的稳定性较好。

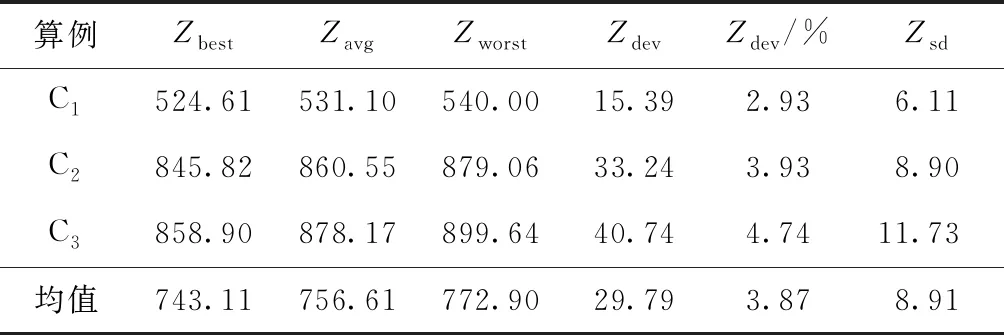
表8 ITTSA的Z值

表9所示为NO-54组合邻域算子下，在C1/C2/C3算例中车辆数的计算结果，其中给出了K的最好值Kbest、平均值Kavg、最差值Kworst、极差值Kdev和标准差Ksd。从表中可见，3个算例的最好结果都下降至最少车辆数，表现较稳定的是C1算例和C3算例，其车辆数保持不变；C2算例中，车辆数为10或11，标准差仅为0.44，波动性较小。说明ITTSA对车辆数的求解效果较好。

表9 车辆数K的计算结果

因为各对比算法的车辆数均已下降至最小值Kmin，所以表10主要给出各对比算法距离值的对比结果。可见，ITTSA在降低距离值方面优于对比文献所使用的算法，除C3算例优化的幅度较小外，C1和C2算例的优化效果均较好。相比算法CA，ICA，ICA+VND，本文ITTSA的平均优化程度比对比文献分别高出5.48%，4.11%，2.06%，可见本文ITTSA的优化能力强于3种对比算法，从而验证了ITTSA的有效性。

表10 各算法的Z值比较

注：Z表示算例的最优距离值；IMP表示ITTSA的Z值高于对比文献的百分比，加粗数据表示最好值。

3.3 回收路径举例分析

本文以C1算例中的计算结果为例，具体回收路径方案如表11所示。针对C1中的50个站点，算法将其分为5条线路进行回收(已达最少车辆数)，线路1包括11个站点，线路2包括11个站点，线路3包括9个站点，线路4包括9个站点，线路5包括10个站点，需要的车辆数为5，总的距离值为524.61。

表11 C1算例的回收路径方案

4 结束语

本文对VRPWFR进行研究，设计了ITTSA并进行求解。经算法测试与文献对比分析，得出如下结论：①在改进的两阶段禁忌搜索算法中，第一阶段的TSP路径优化为第二阶段的VRP路径划分提供了基础；②设计了一个新的线性禁忌表，将邻域算子和邻域交换点对同时作为禁忌对象，能够更好地模拟对候选解的禁忌情况，有效避免重复搜索无效解，提高禁忌效率，并避免过早收敛问题；③对5种邻域算子的组合情况进行测试，结果表明点逆序和点交换这两种算子的组合效果最好；④算法测试与文献对比表明ITTSA具有较好的优化性能。

研究VRPWFR对于促进家具行业的绿色低碳化发展具有重要意义，考虑到供应链中大规模的家具逆向物流问题更加复杂，求解难度也更大，后续将进一步对多级网络同时取送货的家具物流VRP进行研究，构建相应的多目标数学模型，并进一步提升TSA的寻优性能。