具有一般工期与返工的耦合设计任务评审策略分析

王梦娜，王小明，陈庆新，毛 宁

(广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006)

0 引言

定制产品的设计过程由多个设计任务构成，通常以项目形式进行管理。一方面，由于客户提出的产品需求往往不够明确，使得部分设计任务(称为不明确任务)需要经过组长/设计主管评审或客户确认评审后才能完成；另一方面，部分相邻任务在设计内容上具有一定关联(耦合)性，使其返工概率不独立。在市场竞争激烈的今天，企业不仅要尽可能缩短设计项目周期，还要使设计项目完工时间的波动(方差或风险)尽可能小。

在设计项目执行过程中，设计员完成一个不明确任务后可以即刻提交评审，也可以继续下一阶段设计。评审需要一定的准备时间，评审结果为通过或者对设计进行修改(本文称为返工)。在工程实际中，产品试制后可能还需要对设计进行修改，这类修改称为设计变更。本文仅考虑初始设计阶段的评审和返工问题，不考虑产品试制后的设计变更问题。分析可知，将多个任务打包评审能够降低准备时间，但是会增加后续任务出错的风险；反之，如果想避免错误累积风险，则需增加评审准备时间。因此，当设计员面临多种可选的任务评审策略(同时提交评审的任务组合)时，需要准确估计不同评审策略对应的项目完工时间，从中选择最优的评审策略。然而，在设计任务工期服从一般分布且具有随机返工的情形下，往往很难准确估计项目的完工时间概率分布。

在考虑随机返工的网络建模与优化方面，现有研究主要面向系统稳态性能分析和资源配置问题。考虑制造过程中的工件返工和报废，Yu等[1]和Pillai等[2]利用离散时间马尔可夫链建模，分析了工件平均工时、成本和所需原材料数量等指标；王小明等[3-4]针对考虑单次返工的模具订单完工时间预测问题，提出队列长度近似估计与连续时间马尔可夫链相结合的计算方法；Gopalan等[5-6]考虑工件随机返工，基于随机模型研究了有限缓存两级多服务制造系统的工期均值等系统参数；Kao[7]针对单服务自动装配过程中的随机返工问题，采用半马尔可夫理论求解最优策略。另外，部分学者基于马尔可夫理论研究了不带返工的随机项目完工时间预测问题。Kulkarni等[8]最早采用连续时间吸附马尔可夫链建模分析随机项目完工时间概率分布；Dodin[9]针对任务工期服从连续或离散分布的随机网络完工时间预测问题，提出一种包含工期离散化和卷积乘积操作的序贯近似方法；Azaron等[10]提出利用随机动态规划计算随机网络的完工时间均值下界；王小明等[11]提出采用离散时间马尔可夫链状态演化来预测模具项目的交货期。研究表明，马尔可夫链理论能够准确描述随机项目执行过程，在带随机回路的项目网络建模方面更具优势。

本文所研究的设计任务评审决策问题与制造系统质检站定位问题具有一定相似性。在过去几十年，学者们对制造系统质检站定位问题进行了广泛研究，构建了动态规划或整数规划模型，以及对应的精确或启发式求解方法。例如，Chakravarty等[12]研究了多产品流水线质检站设定问题，将质检活动视为加工节点之间的连接弧，提出两种启发式算法求解对应的最短路径模型；Jewkes[13]基于M/G/1排队网模型和多臂老虎机(multi-armed bandits)相关结论，研究了单节点质检频率与生产调度规则联合优化问题；Shiau[14]在考虑有限质检资源约束和质检误差模型的基础上，提出两种简单的启发式算法来分配质检站；Shetwan等[15]对多阶段制造系统中质量控制工作站布局方法进行综述，建立了一般化的模型，并提出高效的启发式求解方法。上述研究主要面向多级串行制造系统，假定每一级只需返工一次且未考虑相邻工作站之间的返工耦合问题，而且均通过返工概率独立估算每一级工作站的工时或成本均值，据此进行确定性转换求解最优质检配置方案。这些研究的方法思路很难应用于设计项目完工时间概率分布估算问题。

对于复杂环境下的项目完工时间预测问题，仿真是一种行之有效的方法[16-17]，其适用于无法得到解析表达式的场景(如模型规模较大或无法得到精确解)，缺点是需要进行大量仿真才能得到比较准确的结果。当解析法和仿真法均可使用时，应优先采用解析法，仿真可用于模型验证。本文以具有一般工期和返工的设计项目为研究对象，研究其完工时间概率分布估算解析模型和方法，以高效准确地评价评审策略的优劣。

1 问题描述

2 数学模型

2.1 PH分布

相型(phase-type, PH)分布是由负指数分布卷积或混合而成的一种概率分布，由具有一个或多个相互关联的泊松过程的系统按顺序或相位发生的结果构成，即PH分布是一种描述连续时间马尔可夫链(Continuous-Time Markov Chain, CTMC)吸附时间的分布。本文采用PH分布对任务工期分布进行近似，并据此计算项目完工时间概率分布。

(1)

式中K0=-Ke为描述中间状态到吸附状态转移速率的n维列向量，e为n维单位列向量。

PH分布的概率密度函数和累积分布函数分别为：

fT(t)=P(T=t)=αeKt(-K)e,t≥0；

(2)

FT(t)=P(T≤t)=1-αeKte,t≥0。

(3)

PH分布的均值和方差分别为：

E(T)=-αK-1e；

(4)

Var(T)=2αK-2e-(αK-1e)2。

(5)

2.2 一般分布下的CTMC建模

2.2.1 任务工期分布近似

PH分布可以使用指数分布的相位，以任意的精确度表示任意正值分布[18]。使用PH分布对一般任务工期进行近似可使项目执行过程具备马尔可夫性，从而便于对其进行建模和分析。在PH分布近似方法方面，Gue等[19-20]和Creemers[21]提出基于平方变异系数C2=σ2/μ2(μ和σ2分别为均值和方差)的近似方法，具体描述如下：

(1)当C2=1时，两者均采用负指数分布来近似任务工期分布。

(2)当C2>1时，Gue等[19-20]采用二阶超指数分布进行近似，Creemers[21]则是采用二相位Coxian分布进行近似。两者的区别在于二阶超指数分布中的两个相位是并行的，二相位Coxian分布的两个相位是串行的。

(3)当C2<1时，Gue等[19-20]采用Erlang分布进行近似，Creemers[21]则是采用亚指数分布进行近似。需要强调的是，Erlang分布是由一系列独立同分布的负指数分布串行构成，而亚指数分布是一般的Erlang分布，即串行独立负指数分布可以是非同等。

上述近似分布的参数计算过程可参考Gue等[19-20]和Creemers[21]的研究。在计算过程中发现，这两种方法都能获得精度较高的概率分布，但是Creemers[21]所提方法对应的马尔可夫链状态数更少(原因是Coxian分布的两相位串行相当于一个任务，而二阶超指数分布两相位并行相当于两个任务)，计算效率更高。因此，本文采用Creemers[21]的近似方法。

2.2.2 项目网络转换

利用2.2.1节所述方法对任务工期分布进行近似后，将原任务执行过程转化为包含一相或多相的随机过程。为了准确描述项目执行过程，在构建数学模型之前需要先对项目网络进行转换，即在添加返工任务节点后，按照PH近似分布将每一相位看作一个虚拟任务节点。

以如图1所示的简单项目为例说明项目网络转换过程。假定任务2和任务3是不明确任务，各个任务的工期平方变异系数C2=1，1/3，2。在评审策略方面，可以将任务2和任务3同时提交评审(称为合并评审策略)，也可以将2和任务3分别提交评审(称为独立评审策略)。限于篇幅，本文仅以独立评审策略为例进行说明，其对应的转换网络如图2所示。需要强调的是，因为同一任务的不同相位被视为一个虚拟的任务节点，所以相位之间的耦合关系本质上与前述相邻任务之间的耦合关系是相同的。另外，从工程实际角度来说，一般只会在任务完工的相位提交评审。

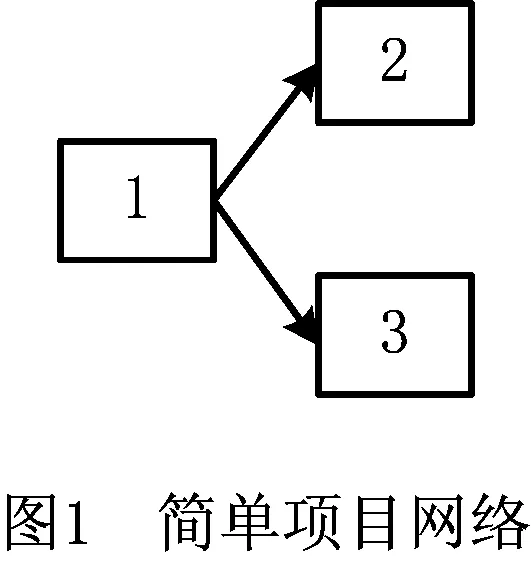
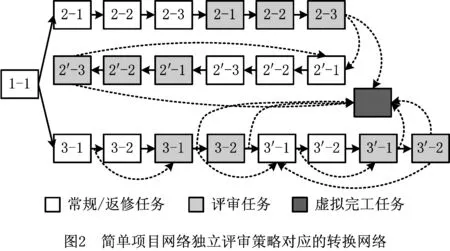
可见，图1所示的项目网络很简单，加入评审策略后的转换网络却比较复杂(如图2)，而且随着原项目网络规模的增大，其后续建模和计算难度也将越来越大。

2.2.3 CTMC建模

经过2.2.2节项目网络转换后，得到一个具备马尔可夫性的转换网络，本节将描述如何采用CTMC对其进行建模。与第1章问题描述类似，假定所得转换网络以单代号网络图G(N′,E′)表示，其中N′=(1,2,…,n′)为任务集合，E′=((j,i)|j,i∈N′)为任务间的紧前约束。从图2可见，转换网络中除了原不明确任务经评审后可能出现的返工任务外，还存在Coxian分布带来的任务跳转(可视为另一种返工)。在原项目网络信息基础上，结合近似分布参数计算，可以获得转换网络中所有任务的工期和返工概率等参数。

显然，当转换网络中的所有任务完工时，项目将永久停留在完工状态。因此，本文需要构建的是一个吸附CTMC模型。吸附CTMC由二元组{X,Q}表示，其中：

(1)系统状态集合XX是由所有可能的项目执行进度状态构成的集合。在近几年基于马尔可夫理论的随机资源受限项目调度研究中，系统状态通常由完工任务集合和在制任务集合构成[21]，或者由空闲任务集合与在制任务集合构成[22]，或者由等待任务集合和在制任务集合构成[23]。因为本文不考虑资源约束，不存在等待任务集合的概念，所以可以直接定义系统状态为在制任务集合，即x=Px。

qx,g(x,j,γj)=pγj/E(dj)。

(6)

同一状态下不同的在制任务率先完工可能导致系统转移至相同的下一状态，此时需要将这些情形下的状态转移速率进行累加，以得到最终的状态转移速率。

2.3 评审策略的评价标准

如前所述，设计项目管理的目标是使项目完工时间尽可能早，且波动尽可能小，即设计任务评审策略的理想评价标准是项目完工时间期望和方差均最小。然而，这两个目标往往难以同时达到，需要进行权衡。这种权衡问题普遍存在于风险投资问题中，学者们在研究这种问题时的主要方法是构建均值—方差优化模型。例如，Markowitz[24]对均值—方差优化方法进行了深入探讨，解释了为何采用均值—方差优化而非均值最优，并对近半个世纪内均值—方差优化的研究进行了综述；Gotoh等[25]探讨了鲁棒经验优化与均值—方差优化的等价性问题；LI等[26]构建了零售商在均值—方差准则下的收益模型；Luo等[27-28]针对产品组合保修政策优化问题，提出最大化利润和风险组合、在限制风险时最大化利润、在满足利润要求时最小化风险3种均值—方差优化方法。

与上述研究类似，本文将项目完工时间期望E(T)和方差Var(T)进行组合，以E(T)+δ×Var(T)作为评审策略的评价函数，其中δ≥0为权衡因子。极端情形下取δ=0，表示只追求项目完工时间均值最小，不考虑其波动性。

3 计算实验

本章以一个典型的模具设计项目为例设计计算实验，分析评审工期(包括工期折扣因子和评审准备耗时)、返工概率、任务关联度等项目环境参数对评审策略的影响。计算程序采用Visual C#编程实现，电脑配置为CPU 2.50 GHz，4 G RAM。

3.1 算例数据

图3所示为包含16个设计任务的典型模具设计项目网络[29]，其中任务2，7，8，14为需求不明确的任务。假定任务对(2,7)和(8,14)有耦合关系，任务7和任务14的工期平方变异系数分别为1/3和2，其他任务节点的工期平方变异系数均为1，所有返工任务的工期均值为其常规任务工期均值的一半，工期平方变异系数与对应常规任务的取值相同。

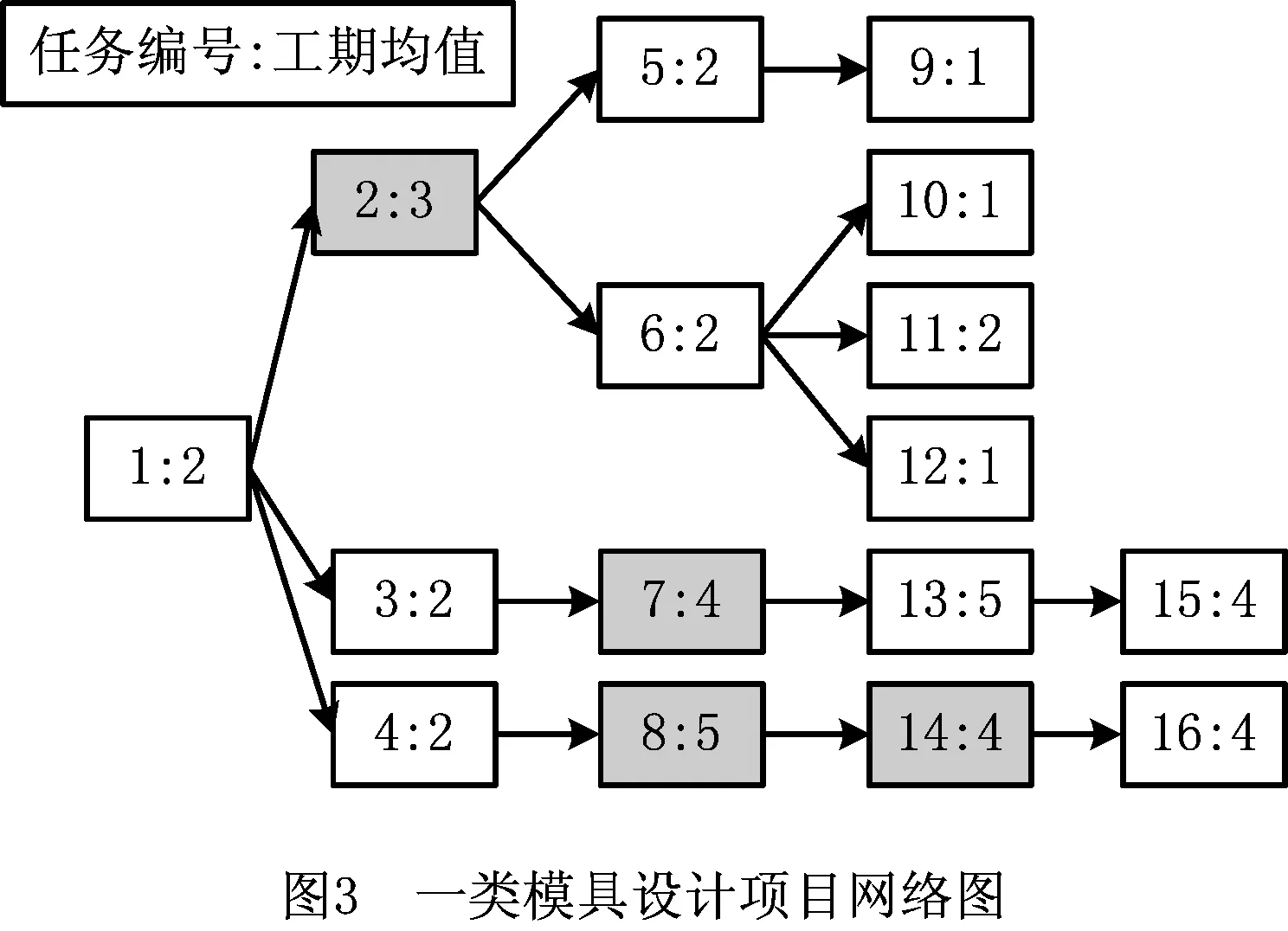
将上述设计项目中的4个不明确任务进行组合，得到15种不同的评审策略。因为部分不明确任务之间不存在耦合关系，而且任务间的进度差异可能较大，所以部分评审策略可直接判断为不合理。例如，任务2与任务8和任务14无耦合关系且进度差异较大，所有将任务2和任务8或任务2和任务14一起评审的策略都不合理。本文实验将分析以下4种评审策略：

(1)策略S1将4个任务分别单独提交评审。

(2)策略S2将任务2和任务7一起提交评审，任务8和任务14单独提交评审。

(3)策略S3将任务2和任务7单独提交评审，任务8和任务14一起提交评审。

(4)策略S4将任务2和任务7一起提交评审，任务8和任务14一起提交评审。

通过对比S1和S2，以及S3和S4，可以分析出并行耦合任务2和任务7是否应该一起评审；通过对比S1和S3，以及S2和S4，可以分析出串行耦合任务8和任务14是否应该一起评审。另外，还将考虑如下不同项目环境参数和决策目标对评审策略的影响：工期折扣因子β={0.8,0.9,1.0,1.1,1.2}；评审准备耗时ζ={0,5,10}；返工概率系数c={0.05,0.075,0.1,0.125,0.15}(设定返工概率P2=3c，P7=4c，P8=4c，P14=3c)；关联度系数r={0.75,1,1.25,1.5,1.75}(设定返工联合概率P2,7=P7,2=P8,14=P14,8=rc)；权衡因子δ={0,1}。

3.2 结果与分析

基于上述实验参数设置，利用本文建模和计算方法获得各评审策略在每组参数组合下的项目完工时间概率分布和目标函数值。为了更清晰地展示实验结果，首先按照δ的不同取值将实验结果分为两组，然后在每一组实验中分别分析其他因素对4种评审策略的影响。第一组实验结果(δ=0)如图4～图6所示，第二组实验结果(δ=1)如图7～图9所示。

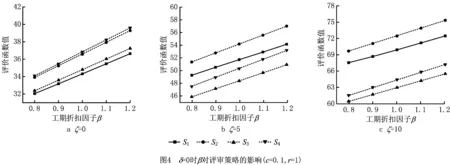
从第一组实验结果可以看出，在仅以项目完工时间期望为评价标准时(δ=0)，4种因素对评审策略的表现均有显著影响。总体来说，当评审固定耗时较小(ζ=0)时策略S1最优，当评审固定耗时较大(ζ=5和ζ=10)时策略S3最优。针对每一种因素的详细分析如下：

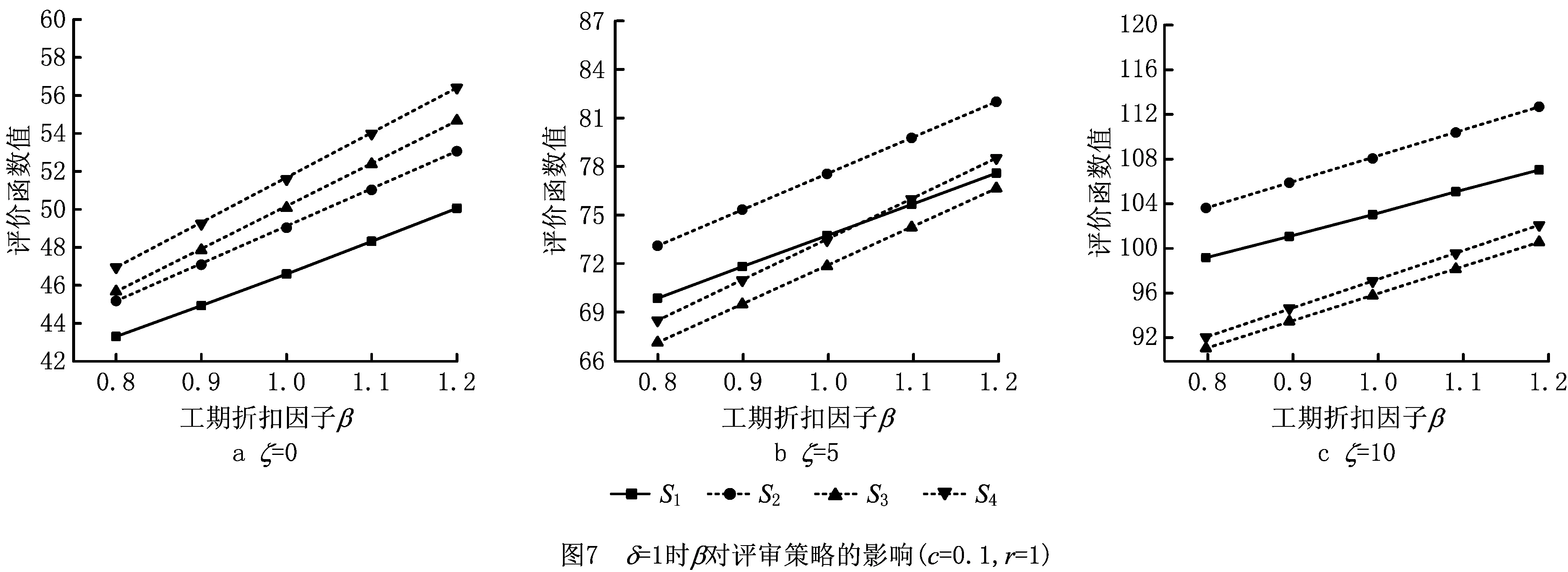
(1)在工期折扣因子方面 所有评审策略目标函数均随β呈正线性增长，如图4所示。在所有ζ取值下，S1均优于S2且S3优于S4，表明并行耦合任务2和任务7单独评审更优。相比之下，串行耦合任务8和任务14的评审更复杂。虽然当ζ=0时，S1优于S3，S2优于S4，但是随着ζ的增长，S3逐渐优于S1，S4逐渐优于S2，而且S1的目标函数比S3的目标函数增长得更显著。原因是，S1会同时增长4个评审节点的工期，而S3只增长3个。简而言之，串行耦合任务组合评审策略在ζ较小时可能不是最优，但是随着ζ的增长会逐渐表现出优势。

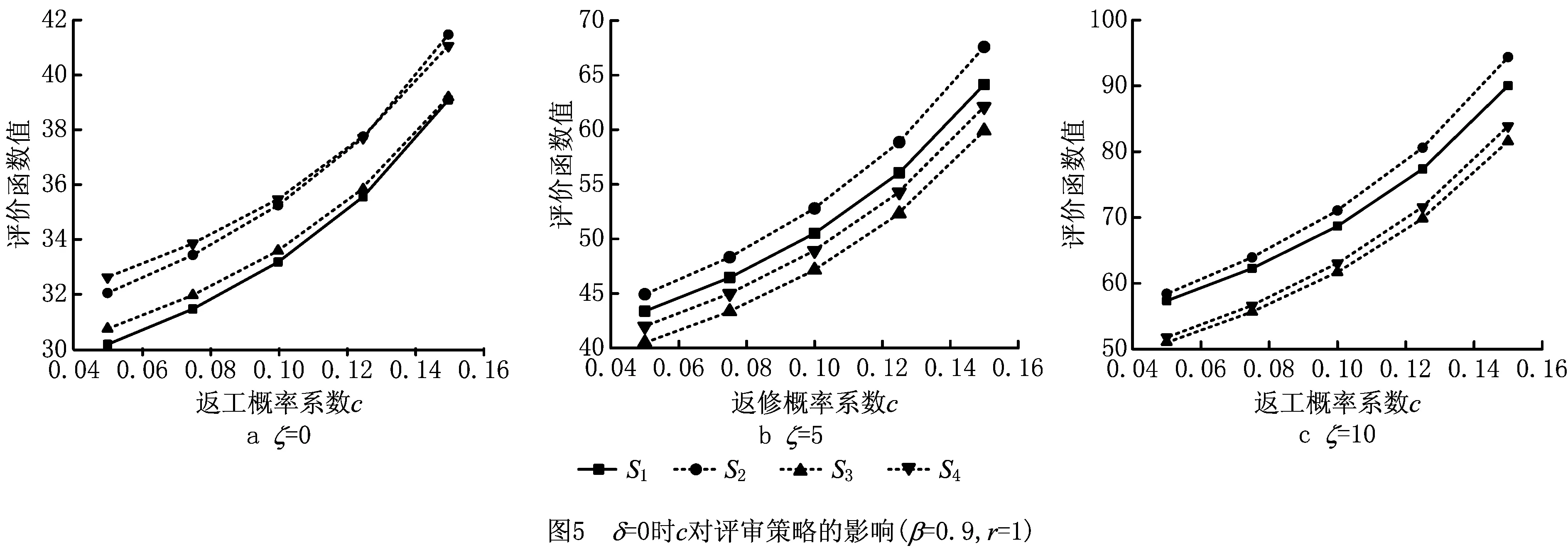
(2)在返工概率系数方面 所有评审策略对应的函数值均随c的增长呈多项式增长，如图5所示。4种策略表现的优劣与图4所示结果相同，其内在原因也与上述分析相同。

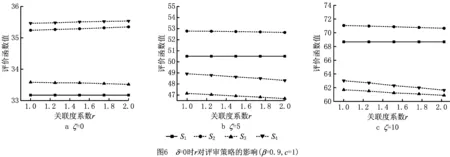
(3)在关联度方面S1对应的函数值与r无关，S2，S3，S4对应的函数值与r呈线性关系，如图6所示。由于S1中4个任务独立评审，关联度的改变对CTMC没有影响。相比之下，S2，S3，S4均有组合评审，关联度变化会同时影响评审准备时间和任务等待时间。对于串行耦合任务8和任务14，关联度越大意味着其累积错误的风险越高，理论上应该独立评审，但是独立评审将增加评审准备时间。对于并行耦合任务2和任务7，关联度增大将导致系统以更大的概率转移至这两个任务同时返工的状态，即增加等待时间。因此，S3对应函数值一直与r负相关，S2和S4对应的函数值与r之间的关系则随ζ的增长由正相关变为负相关。总之，4种策略的表现优劣与图4所示结果相同，其内在原因也与上述分析相同。

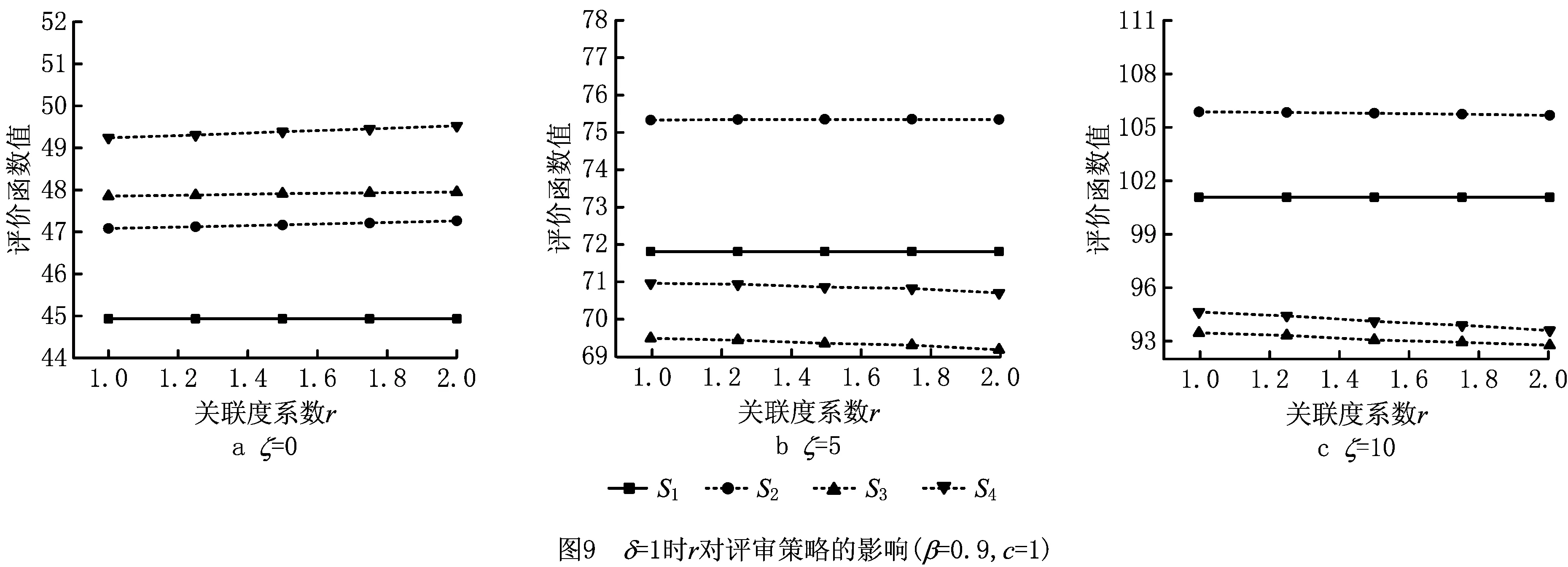
从第二组实验结果可以看出，当以项目完工时间期望和方差组合(δ=1)为评价标准时，4种项目环境因素对评审策略的表现同样有显著影响。总体来说，第二组实验结果与第一组实验结果相似，区别在于图7和图8显示部分策略之间存在交叉，表明在不同评审策略评价标准下，几种策略的优劣表现为部分环境下存在差异。造成这个现象的原因是PH分布的均值和方差同向变化(同时增加或减少)，但是变化速率不同。

上述实验结果给设计项目管理工程实际带来以下两方面重要启示：①应该根据所处项目环境选择合适的评审策略。在大多数情形下，并行耦合任务应独立评审，串行耦合任务在评审耗时较小时应独立评审，反之则应组合评审。②应该集中精力降低返工概率，因为项目完工时间随返工概率呈多项式增长，随其余因素呈线性增长。从管理角度来说，可以通过加强与客户的有效沟通、规范需求分析与设计过程等方法来降低返工概率。

4 案例分析

为了验证本文所构建模型和方法的工程实用性，同时验证上一章所得实验结论的可靠性，本章以深圳某企业的一套模具设计过程为例进行分析。

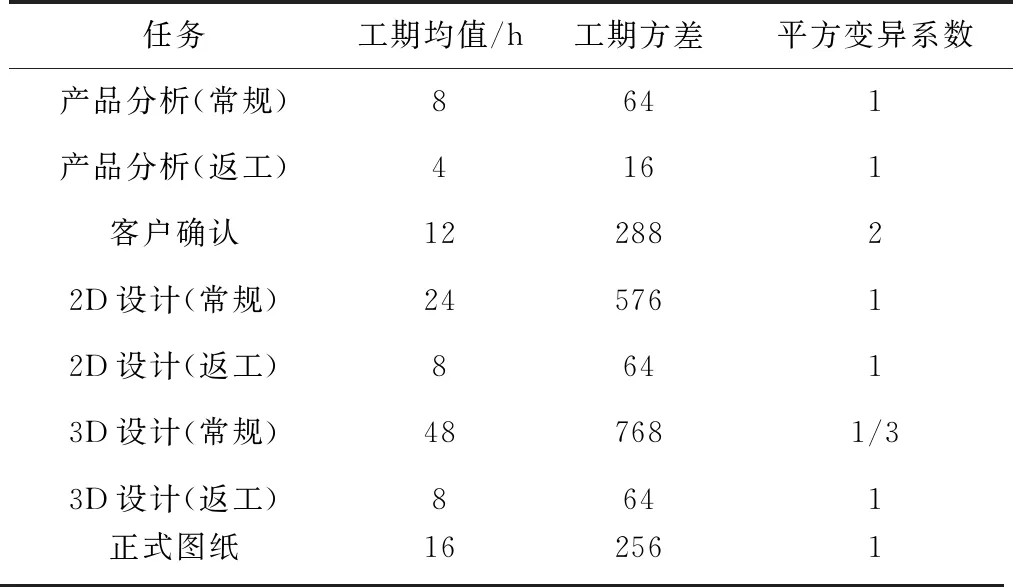
该企业模具设计包括产品分析、2D设计、3D设计和出正式图纸等几个步骤，流程如图10所示。通过历史数据统计，得到如表1所示的任务工期参数信息。

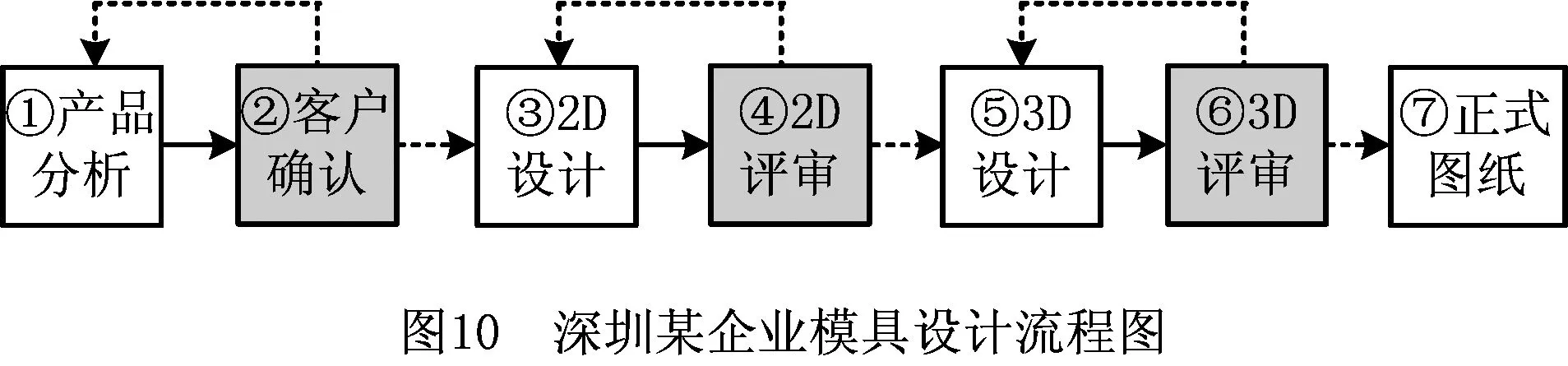
表1 任务工期参数信息

任务工期均值/h工期方差平方变异系数产品分析(常规)8641产品分析(返工)4161客户确认1228822D设计(常规)2457612D设计(返工)86413D设计(常规)487681/33D设计(返工)8641正式图纸162561

产品分析需要提交客户确认，2D和3D设计后需要提交组长/设计主管评审，三者串行耦合。因为客户要求先进行确认，而且客户确认后可以提前采购部分大型物料，所以产品分析不会与2D和3D设计组合评审。统计得知，客户确认后的返工概率为0.25，2D和3D评审每次准备耗时ζ大约在0.5～1 h，工期折扣因子β=0.167，2D评审的返工概率为0.5。若2D评审后再进行3D设计，则3D评审的返工概率为0.3，否则将因错误累积而增至0.6。

该企业当前是将2D和3D单独评审，需要分析其与组合评审策略哪种更优：①策略S1，将2D和3D设计单独提交组长/设计主管评审；②策略S2，将2D和3D设计一起提交给组长/设计主管评审。

采用本文所建模型与方法得到表2所示的结果。若仅以完工时间均值作为评审策略的评价标准(δ=0)，则独立评审策略S1在ζ≤1时更优，而组合评审策略S2在ζ=2时更优；若以完工时间和方差同时作为评审策略的评价标准(δ=1)，则独立评审策略在3种情形下均更优。由此可见，企业当前的评审策略是合理的，该结果与本文实验结论一致。

表2 两种评审策略的计算结果

如前所述，企业可以通过提高设计员能力、加强与客户的有效沟通等方式降低返工概率。为了更全面地分析上述案例并进一步验证本文实验结论，在假定该企业降低返工概率的情形下对比两种策略的优劣。不失一般性，假定客户确认后的返工概率降为0.2，2D评审的返工概率降为0.3，2D评审后再进行3D设计的3D评审返工概率降为0.2，因错误累积的3D评审返工概率降为0.4，计算得到表3所示的结果(其中Dev(E(T))%和Dev(Var(T))%分别表示项目完工时间的均值和方差与表2结果的偏差百分比)。可以看出，相比表2，降低返工概率后，项目完工时间均值和方差均显著减小(下降约6%)。在低返工概率下，策略S1对应的E(T)和Var(T)在3种情形下均小于策略S2的对应值，即S1优于S2。另外，随着ζ的增长，两种评审策略之间的差距明显缩小，其原因同第3章实验结果的详细分析。

表3 降低返工概率后的两种评审策略计算结果

5 结束语

本文针对具有一般工期和随机返工的设计任务评审策略分析问题，基于PH分布构建了项目完工时间概率分布估算解析模型。实验结果表明，项目环境因素对评审策略的表现有显著影响，没有哪种策略在所有环境下均最优。一般来说，并行耦合设计任务应独立评审，串行耦合设计任务在评审准备时间较小时应独立评审，否则应组合评审。本文研究还发现，返工概率是影响设计项目完工时间的首要因素，企业应重点利用有效沟通和规范设计等方式来降低任务返工概率。最后，通过深圳某企业模具设计过程应用案例验证了模型和方法的有效性。

本文所构建的模型和方法具有一定普适性，对研发评审、制造质检等问题均具有一定指导意义。然而，当项目网络规模较大时，PH分布会面临大规模矩阵运算无法求解的问题，采用仿真等方法是更好的选择。下一阶段工作将研究对应的评审策略动态优化问题。