考虑人因的多目标拆卸线平衡问题及改进风驱动算法求解
2020-06-13张则强曾艳清
张 颖,张则强+,曾艳清,蔡 宁
(1.西南交通大学 机械工程学院,四川 成都 610031;2.轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)
0 引言
随着工业4.0和大数据分析时代的来临,产品更新换代节奏加快,大量废旧产品等待处理,为减轻国家压力和环境负担,必须对废旧产品进行回收再制造。与传统制造企业追求效率、成本和个性化为一体相比,再制造服务企业需兼顾时代的先进性和社会资源的紧缺性,而作为一种综合性服务模式,其包括个性化需求服务与生产性服务[1]。拆卸线是实现再制造最关键的环节之一,属于面向社会的生产性服务,其效率直接影响拆卸成本[2],然而长期依赖人工操作的拆卸线在短时间内很难实现无人化操作,在生产过程中,企业既要注重自身效益,又要注重人的因素,因此制造企业在平衡拆卸线时有必要从人因工程学的方面进行考虑。
拆卸线平衡问题(Disassembly Line Balancing Problem, DLBP)[3]在将近18年研究中得到了广泛推广与应用,同时也衍生出许多应用于DLBP的求解方法,最先使用的是启发式算法[3-5],后又发展到数学规划方法[6]和智能算法[7-12]。DLBP是NP-完全问题[13],在使用线性加权方式求解的结果中只能得到一个可行的拆卸序列,且求解结果缺少对比性和可选性。为探索更优的拆卸线平衡方案,部分学者提出与启发式方法类似的数学规划方法,但其实质仍是转化为单目标求解,因为NP-完全问题的遍历空间会出现随任务规模的增大呈指数级增长的现象,所以数学规划方法并不适用于求解大规模拆卸任务问题。近年来,因智能算法具有鲁棒性和通用性强、寻优效果好及无需特殊信息等优点而被广泛应用到拆卸线中,包括蚁群优化(Ant Colony Optimization, ACO)算法[7]、粒子群优化(Particle Swarm Optimization, PSO)算法[8]、禁忌搜索算法(Tabu Search algorithm, TS)[9]、变邻域搜索算法[10]等,然而上述文献对多目标进行处理的方法均为字典顺序法,其实质仍是将问题转化为单目标求解。为保留多个子目标的原始状态,并规避转化为单目标求解的缺陷,文献[11]引入Pareto解集思想和ACO算法求解DLBP。
在废旧产品的完全拆卸[3-13]中,主要以工作站数、零件需求、拆卸成本、空闲时间均衡指标、危害度、平滑率等为目标函数。针对拆卸线的复杂性和多变性,越来越多的学者针对不同的拆卸情况进行研究,Paksoy等[14]建立了模糊目标混合模型,首次将二元模糊目标规划和模糊多目标规划方法应用于混合模型DLBP,以考虑决策者的模糊愿望;Tuncel等[15]研究大规模不确定性拆卸线,其运用强化学习的方法处理DLBP,并能在具有确定性的随机环境中操作;Zhang等[16]认为在拆卸过程中存在许多对操作效率有影响的不确定性因素,对考虑模糊作业时间的多目标DLBP进行了研究。以上文献在拆卸生产线中以利润和效率为主导,忽略了操作中对人的影响,未能实现人—机—环境之间的最佳匹配。Garnahan等[17]认为在工人操作过程中忽略作业任务对操作工人的体力要求,仅考虑作业任务的优先级和最小化空闲时间指标是不够的;Zhu等[18]在拆卸线中考虑零件的危害性,认为废旧产品在拆卸过程中存在的安全隐患对工人的身心健康构成潜在危害,应该评估并考虑拆卸操作中涉及的这些危险;Al-Zuheri等[19]表明,在设计或重新设计步行工人装配线时,兼顾对人体工程学性能的影响不仅能减轻工人的负担,还能能保证生产效率;Baykasoglu等[20]也指出装配线中的人体工程学对生产率和工人健康都有影响。因此,将人体工程学考虑进拆卸生产线中具有实际意义。
风驱动优化(Wind Driven Optimization,WDO)算法[21]模拟空气质点在空气中的受力情况,是一种基于群体驱动的迭代式全局优化算法。目前,该算法主要应用于图像处理[22]、电磁优化问题[23]、云资源调度[24]等,既可解决连续性问题,也可求解离散优化[23]问题,相比于其他智能算法,其速度和位置更新方程更具实际意义,应用前景十分宽广。然而,该算法在其他领域还未取得和智能算法一样的地位,因此在更广阔的工程应用中研究WDO算法具有实际意义。
现有的再制造企业大多是劳动密集型企业,而DLBP中未考虑人的情况,企业应适当站在工人的角度考虑,降低劳动损害、提高操作舒适度。在此基础上,本文提出考虑人因的拆卸线平衡问题(Human Factors Disassembly Line Balancing Problem, HFDLBP),建立考虑人因的多目标数学模型,并运用改进的离散多目标风驱动优化(Multi-objective Improved Wind Driven Optimization,MIWDO)算法求解所提模型。首先,在算法中引入基于任务的编码方式,然后根据拆卸任务的优先关系产生初始解;其次,重新定义风驱动优化算法的速度更新和位置更新的相关操作,通过变邻域搜索策略改进任务在拆卸序列中所处位置的局部搜索;最后,引入Pareto思想和拥挤距离筛选机制[25]处理多目标问题,并保留迭代过程中的较优解。
1 基于人因的DLBP数学模型
1.1 基于人因的DLBP问题描述
经实地调研,常见的拆卸生产线在拆卸操作过程中长期依赖人工操作。由于拆卸任务是简单的重复性动作,企业根据平均作业强度设置有宽限时间,可以使工人得到适当的脑力和心理调节。在拆卸操作过程中根据零件的特殊性和复杂性,将拆卸操作姿势分为站姿和坐姿两种操作。同一工作站内,如果同时有必须站姿操作的任务和坐姿操作的任务,则为了保证生产效率和节省体力,会一直保持站姿操作完成该工位上的所有任务[26]。因此当指派任务到工位时,在满足既定约束的前提下,尽量将相同操作姿势的任务安排在同一工位。表1所示为6个任务的拆卸信息,包括任务编号、零件的拆卸时间、拆卸成本和操作姿势。

表1 任务拆卸信息
表1第4列中,操作姿势为1时表示该任务必须使用站姿操作,如果只考虑工作节拍为9 s,则任务分配组合可为{1,2},{3,4},{5,6},此时空闲时间为0,最大程度上满足了空闲时间指标约束,而且3个工作站中都有必须使用站姿操作的任务,都必须为站姿工作站。考虑到站姿操作不如坐姿操作舒适,应该将站姿操作的任务尽量分配到相同的工作站,以减少站姿操作工作站,因此在满足优先关系约束的前提下可将任务1和任务6分配到同一工作站,从而减少一个站姿操作工作站。
1.2 考虑人因的数学模型
鉴于某些零件是否拆卸影响其他零件的拆卸难易程度和完好程度,将待拆卸产品根据作业任务优先关系分为不可继续拆卸的单个零件。模型假设:①所有零件均拆卸;②所有拆卸任务得到的是不可再分的零件;③待拆卸产品无限供应且零件齐全;④拆卸的产品为单一产品;⑤拆卸线为直线布局;⑥每个工作站的人数相同;⑦工人操作的熟练度一致,而且采用轮岗操作;⑧拆卸时间已知,不考虑流转时间;⑨没有任何突发状况。
(1)决策变量
(2)参数说明
K为拆卸过程中允许开启的最多工作站数目,无特殊情况下K=n;
CTw为工作站生产节拍;
j为工作站编号,j=1,2,…,K;
n为待拆卸零件总数;
i,l为任务编号,i,l=1,2,…,n;
xij表示第i个任务分配到第j个工作站上;
PRTi为第i个任务的操作时间;
UTi为第i个任务的单位时间拆卸成本;
STj为第j个工作站的实际生产时间(单位:s);
SUi为任务i的操作姿势。
(3)目标函数
F=min[F1,F2,F3,F4]。
(1)
工作站数目指标
(2)
工作站的开启数直接影响拆卸成本和管理难度,因此应使工作站数目最小。
工作站空闲时间均衡指标
(3)
式中
(4)
式(3)为空闲时间均衡指标,为了避免上下游工作站之间因工况不一而产生拥挤堵塞和闲置的情况,空闲时间均衡指标需尽可能的小;式(4)表示每个工作站的实际工作时间为分配到每个工作站实际任务的拆卸时间之和。
拆卸成本
(5)
任务的单位时间拆卸成本已知,企业拆卸一件废弃产品时,拆卸成本越小越好。
站姿工位数
(6)
考虑人因,为减少体力消耗并提升操作舒适度,尽量将站姿操作的任务放在同一工作站。
(4)约束条件
(7)
(8)
(9)
STj≤CTw,∀j∈{1,2,…,K};
(10)
∀i,∀l∈{l|bil=1},∀j∈{1,2,…,K};
(11)
(12)
(13)
(14)
2 求解基于人因的拆卸线平衡问题
2.1 初始解的产生
待拆卸产品的零件采用实数编码的形式,设待拆卸产品的零件个数为n,则i=1,2,…,n,任务之间存在优先关系约束。以图1的任务优先关系图为例,图中圆圈内的数字表示任务编号,箭头始端的任务为箭头终端任务的紧前任务。
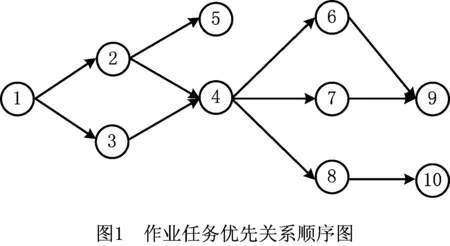
为便于操作,需将拆卸作业任务的优先关系图转换成优先关系矩阵
B=(bil)n×n
(15)
式中:i,l=1,2,…,n;bil为0-1变量,若任务i为任务l的紧前任务,则bil为1,否则为0。采用优先关系矩阵构造初始解,将图1的任务优先关系顺序图转换为优先约束关系矩阵(如图2),初始解通过优先关系矩阵产生,随机选择没有紧前任务的任务,然后解除该任务对后续任务的约束,直到所有任务均加入拆卸序列为止。

2.2 风驱动优化算法离散化
由大气动力学知识可知,影响风驱动的力主要有气压梯度力、摩擦力、重力及科氏力,空气质点在4个力的作用下向最优位置靠近。重新定义速度和位置的相关操作,并采用WDO算法解决离散型问题。与连续型WDO算法类似,空气质点中的速度更新公式和位置更新公式分别为:
(16)
xnew=xcur⊕(μnew×Δt)。
(17)


(2)位置离散化 待拆卸的产品有n个任务,通过优先约束关系矩阵产生的种群即为可行拆卸序列X(x1,x2,…,xn),可行拆卸序列的n个维度值表示任务的编号,任务的编号不同且不重复。位置加法记为“⊕”,设Δt=1,根据有效交换对对Xcur中的拆卸序列进行处理,每一个有效交换对产生一个新的位置。
2.3 多目标处理
采用Pareto的思想处理有J个子目标的最小化问题,解空间中的任意两解Z1和Z2,若满足式(18)中的关系,则Z1支配Z2。
(18)
驱动开始时,通过优先关系约束矩阵B随机生成初始种群,通过邻域操作产生初始种群的局部最优和全局最优,本文在空气质点跟随局部最优和全局最优的过程中,均采用Pareto解集思想和拥挤距离机制对多目标进行筛选。初始种群通过变邻域操作产生邻域操作空气质点和邻域操作解,然后进行Pareto操作得到局部最优解,随机选择一个局部最优作为空气质点的局部最优空气质点,整合局部最优空气质点得到的所有近似Pareto解即为全局最优。邻域操作多目标处理如图3所示。

采用NSGA-Ⅱ拥挤距离机制[25]对超过外部档案个数的非劣解进行筛选,淘汰拥挤区域的解,获得均匀分布的近似Pareto最优前沿。设定边界解Cd1=Cdp=∞,对于i=2,3,…,p-1的解,计算非边缘解的拥挤距离:
(19)
2.4 算法流程
MIWDO算法流程步骤如下:
步骤1输入问题参数,包括优先关系矩阵B、总任务数n、工作站节拍CTw、拆卸成本UT、任务的操作姿势SU。
步骤2输入算法参数,包括种群规模pop_num、最大驱动次数Max_gen、初始搜索深度r0、终止搜索深度re、摩擦系数α、重力加速度g、气压梯度力RT、科里奥利力(科氏力)c、外部档案规模Out_0、时间变化量Δt。
步骤3初始化种群、外部档案和目标值。
步骤4根据优先约束关系矩阵B产生初始种群,并计算其目标值,更新局部最优位置p0和目标值F(p0),更新外部档案Q。
步骤5设置搜索深度rh=r0,进行i=1次驱动迭代。
步骤6对种群中的空气质点进行邻域搜索,将搜索深度设置为rh,驱动i次,每次更新局部最优位置pi、目标值F(pi)、外部档案Q。
步骤7计算Q的个数,如果Q_num>Out_0,则根据式(19)和式(20)计算各非劣解的拥挤距离,根据拥挤距离进行降序排列,选取前Out_0个非劣解,得到新的Q,执行步骤8;如果Q_num≤Out_0,则直接执行步骤8。
步骤8在Q中随机选定一个全局最优位置gi和目标值F(gi)。
步骤9根据式(16)和式(17)分别更新空气质点的速度和位置,计算更新后的目标值,更新种群与外部档案Q。
步骤10每驱动Max_gen/(r0-re)次,搜索深度rh减少一次。
步骤11判断i MIWDO的操作流程如图4所示。 采用MATLAB R2010b开发MIWDO算法程序,在Intel(R)Core(TM)i5-4210 U CPU、2.4 GHz主频、4 GB内存的计算机环境下运行程序。通过求解文献[4,11]研究的P10和P52算例对MIWDO算法的可行性和有效性进行验证,并通过与其他算法的求解结果进行对比证明所提算法适用于求解DLBP。 小规模算例以文献[4]的P10算例为例,仍以工作站数目f1、空闲时间均衡指标f2、危害指标f3和需求指标f4为目标进行优化,通过在不同参数值下运行程序,选取结果相对较优的参数值作为小规模算例的参数值。输入算法的参数为:种群规模pop_num=15,最大驱动次数Max_gen=20,初始搜索深度r0=5,终止搜索深度re=2。输入问题的参数为:节拍时间CTw=40 s,摩擦系数α=0.4,重力加速度g=0.2,气压梯度力RT=1.0,科里奥利力(科氏力)c=0.2,外部档案规模Out_0=10,Δt=1。程序运行10次,运行结果与Greed/2-Opt[4]、新启发式(New Heuristic, NH)算法[5]、ACO[7]、TS[9]和人工蜂群算法(Artificial Bee Colony algorithm, ABC)[12]所求得的结果进行比对,每个目标最优值用粗体表示,如表2所示,其中编号6~12的解均为MIWDO算法求得。 表2 各算法求解P10问题的分配方案 3.1节验证了MIWDO算法在小规模算例中的可靠性和适用性,为验证该算法同样适用于大规模问题,以文献[11]的P52算例作为研究对象,考虑到可比性,仍对原文献的3个目标进行求解,并与ACO[7]、目标驱动离散布谷鸟搜索(Goal-driven Discrete Cuckoo Search,GDCS)算法[27]、人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)[28]、细菌觅食优化(Bacterial Foraging Optimization, BFO)算法[29]、改进猫群优化 (Improved Cat Swarm Optimization, ICSO) 算法[30]和遗传模拟退火算法(Genetic Algorithm and Simulated Annealing, GASA)[31]进行对比。 综合考虑算例特性和算法结构,同小规模算例类似,将程序在不同参数值下运行,选取结果相对较优的参数值作为大规模算例的参数值。算法参数设置如下:种群规模pop_num=100,最大驱动次数Max_gen=200,初始搜索深度r0=26,终止搜索深度re=2,节拍时间CTw=600 s,摩擦系数α=0.8,重力加速度g=0.6,气压梯度力RT=2,科里奥利力(科氏力)c=0.2,外部档案规模Out_0=10,Δt=1。程序运行10次,选取其中1次的结果,得到10组可行解,各目标最优值用粗体表示,如表3所示。通过10个结果可知,MIWDO算法的平滑率在0.871 7~0.999 6之间,平均闲置率均为0.057 9,拆卸成本在127.056元/台~135.300元/台之间。 表3 P52项拆卸任务的求解结果 续表3 与求解P52问题的GDCS,AFSA,BFO,ACO,ICSO,GASA,MIWDO 7种算法进行对比,结果如图5所示。由图5a可知,MIWDO算法求得的结果包围其余6种算法的解,说明MIWDO算法更优; 图5b为综合几种算法的最新近似Pareto前沿,可见MIWDO算法求得的解支配以上算法求得的解,证明MIWDO算法适用于求解大规模完全DLBP。 为了进一步验证MIWDO算法的可靠性和所提模型的适用性,将MIWDO算法和所提模型应用于某型号打印机拆卸生产线,某打印机的55个拆卸任务优先关系如图6所示,表4所示为拆卸任务的拆卸信息。 经过多次调整算法参数,最终参数设置如下:CTw=150 s,种群规模pop=100,驱动次数Max_gen=200,初始搜索深度r0=28,终止搜索深度re=2,摩擦系数α=0.8,重力加速度g=0.6,气压梯度力RT=2.0,科里奥利力(科氏力)c=0.2,外部档案规模Out_0=10,Δt=1。程序运行10次,取其中1次运行结果,得到8个可行解,如表5所示。根据MIWDO算法求得的解可知,开启的工作站数均为F1=5个;空闲时间指标F2在1 125 s~1 373 s之间,考虑到站姿操作工位数尽可能少,空闲时间均衡指标会偏高;待拆卸产品的拆卸成本F3在5.895元/台~6.555元/台之间。由表5可知,在开启工位数一致的情况下,拆卸成本、空闲时间指标、站姿工位数、拆卸成本4者最优不可兼得;在拆卸空闲指标相当的情况下,站姿操作工位越少,拆卸成本越高,例如方案2和方案1,站姿工位数F4减少25%的代价是空闲时间指标F2提高0.178%、拆卸成本F3提高3.8%,说明减少坐姿工作站不会对空闲时间和拆卸成本造成过大影响。因此,若优先考虑空闲时间指标最小,则可选择方案1、方案2和方案7;若优先考虑拆卸成本最小,则方案3、方案6和方案8是可行选择;若优先考虑人因,最小化站姿操作工位数,则可选择方案4、方案5和方案7。 表4 打印机55个拆卸任务的拆卸信息表 表5 MIWDO算法求解HFDLBP的结果 续表5 本文在拆卸线中考虑人因,将工位分为站姿工位与坐姿工位,在开启工作站数目、空闲时间均衡指标和拆卸成本的基础上加入站姿工位数目指标,建立了考虑人因的多目标DLBP的数学模型,并运用MIWDO算法对模型进行求解。针对现有文献中采用WDO解决离散多目标问题的实例较少的现状,对WDO进行离散化处理,重新定义速度和位置更新操作,并采用Pareto解集思想和拥挤距离筛选机制处理多目标问题。采用P10和P52算例对算法进行验证,并与其他算法进行对比分析,验证了该算法的有效性和可行性。最后,将所提算法应用于考虑人因的某打印机DLBP中,并与未考虑人因的情况进行对比,证明考虑人因更具前瞻性。 在完全DLBP的基础上加入人的因素,在考虑企业经济因素的同时考虑拆卸线操作对人的影响更具实际意义。拆卸线在考虑人因的应用上还有很大的开发领域,后续可根据实际情况在拆卸线中加入人的心理疲劳、脑力疲劳和身体负荷承受度等进行深入研究。3 算法验证
3.1 小规模算例



3.2 大规模算例



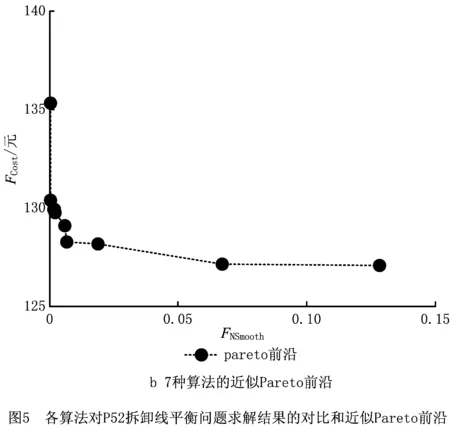
4 实例应用
4.1 考虑人因的拆卸线平衡问题应用

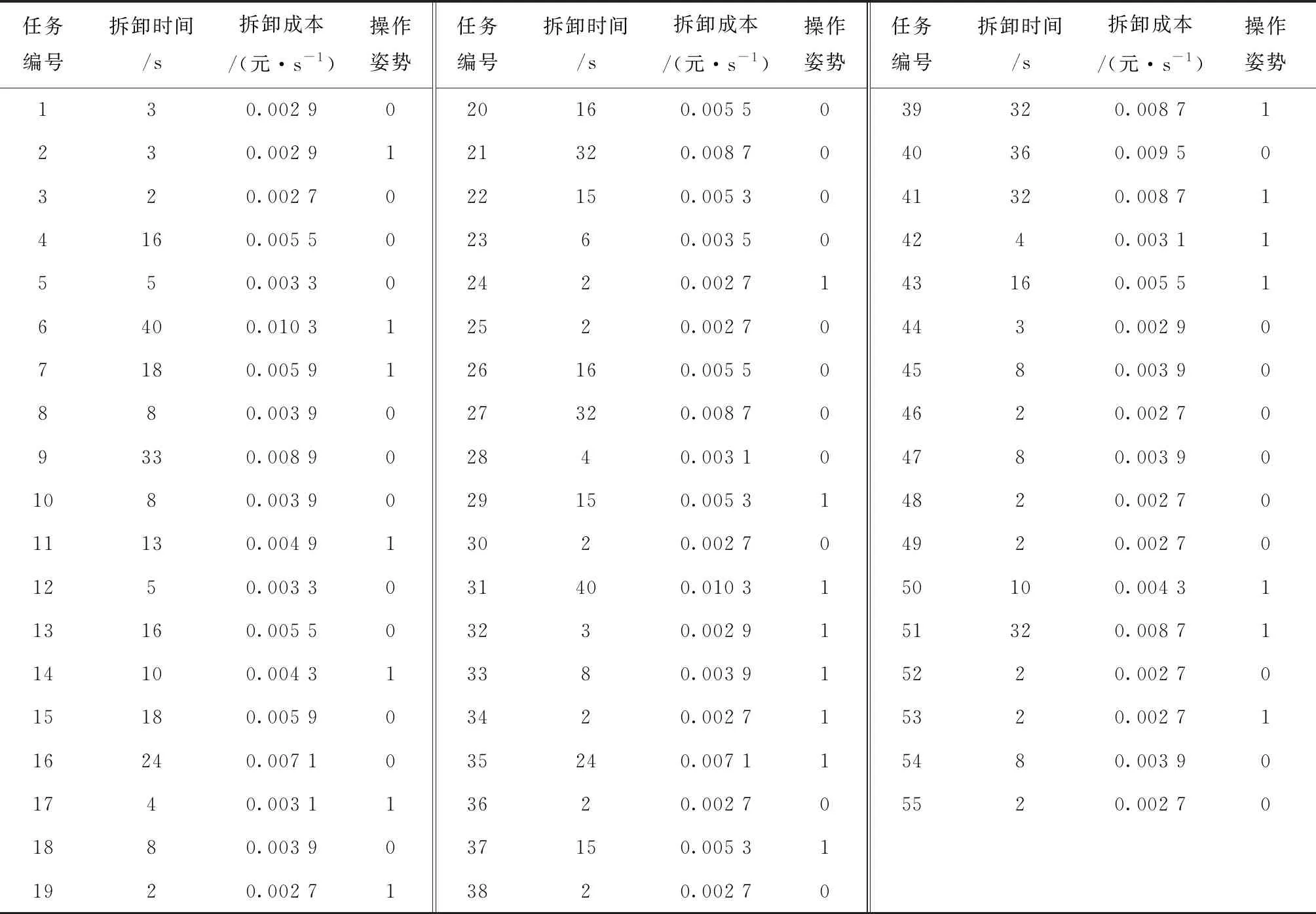


4.2 拆卸线平衡问题实例应用
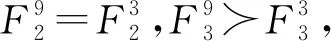




5 结束语
