利用微米划痕研究TiN涂层的失效机理
2020-06-12高诚辉
刘 明, 李 烁, 高诚辉
(福州大学 机械工程及自动化学院, 福建 福州 350116)
1 引 言
TiN涂层具有高硬度、低摩擦系数、优良的抗氧化性和耐磨性而广泛应用于切削和成形工具[1,2]。涂层与基体的界面结合性能和刀具磨损状态是决定涂层可靠性与使用寿命的关键因素。因此,需要对刀具的磨损状态进行检测[3,4],并选择合适的方法(如压痕实验[5~10],划痕实验[11~14]等)研究涂层的失效机理和磨损性能。
Hainsworth等[11]采用微米划痕研究了不同基体下的TiN涂层,发现摩擦系数会随着载荷的增加而稳定地增加。不仅载荷与摩擦系数有关,表面粗糙度也是重要的影响因素。Larsson等[12]通过划痕试验研究了高速钢上TiN涂层的失效机理,发现摩擦系数的大小会受到涂层表面粗糙度的影响。Kataria等[13]则从不同的划痕模式入手,对摩擦系数进行了研究,结果发现:在不同的划痕模式下,摩擦系数的变化趋势不同,且摩擦系数的大小与划痕往复磨损次数有关。为了进一步分析影响摩擦系数的因素,Wang等[14]进行了较为系统的研究,发现:TiN涂层的内在因素(显微结构、硬度和厚度等)和测试因素(载荷、润滑和温度等)均会影响摩擦系数的大小和变化趋势。虽然对摩擦系数的研究较为深入,但是划痕过程中摩擦系数的波动机理尚不清楚,需要相关分析和深入探讨。
本文采用微米划痕实验方法对TiN涂层的失效机理进行研究,分析了TiN涂层的失效过程,阐明了表面形貌与涂层失效对摩擦系数波动影响的机理,并评估了TiN涂层的断裂韧性。
2 TiN涂层微米划痕实验
划痕实验所用的样品是采用PVD方法在不锈钢基体上沉积的TiN涂层,尺寸为40.6 mm×20.4 mm×10.4 mm。涂层的厚度为3~5 μm。实验采用半径100 μm、锥角120°的Rockwell C金刚石压头和渐进载荷与恒定载荷2种加载方式。渐进载荷加载参数:滑动速度3 mm/min,划痕距离3 mm,加载范围30 mN~30 N; 恒定载荷加载参数:载荷7 N和13 N,滑动速度1 mm/min,划痕距离1 mm。
划痕仪上安装的声发射(AE)传感器用于检测裂纹的产生和涂层失效。实验首先对TiN涂层进行预扫描,然后进行微米划痕实验,最后对划痕形貌进行后扫描。采用光学显微镜和扫描电子显微镜(SEM)观察划痕形貌,并采用白光干涉仪测试了涂层表面的粗糙度。
3 TiN涂层微米划痕结果分析
Homberg等[15]对金刚石球形压头在涂层样品表面滑动的变形行为进行了研究,并采用有限元模拟分析了划痕过程中的应力和裂纹形式,发现:材料的接触和变形机理可分为犁耕、界面滑动和断裂3个阶段。
犁耕阶段包括基体材料的弹塑性变形以及划痕凹槽的形成。界面滑动阶段主要由涂层的弯曲和拉伸组成。压头在涂层表面滑动时伴随着应力的产生和应力释放。
采用SEM对TiN涂层的3个区域进行了分析。在第1个区域中,与先前研究TiN涂层的第一种失效形式不同(正向V形裂纹或平行裂纹)[12,15],观察到反向V形裂纹如图1(a)所示。反向V形裂纹几乎是对称地排列在划痕的两侧,类似鱼骨。反向V形裂纹的形成主要是由于金刚石尖端在沿着划痕方向推动涂层时,两侧发生应力集中[16],即压头下方的涂层被拉时,发生了拉伸弯曲。
在第2个区域中,这些反向V形裂纹逐渐转变为平行裂纹,如图1(b)所示。与反向V形裂纹相比,平行裂纹的长度相对较长。图1(b)中还有部分未转变为平行裂纹的反向V形裂纹和转变后的正向V形裂纹。同时,划痕过程中产生一些磨损颗粒,磨损颗粒大多来自于涂层的表面。
在第3个区域中,平行裂纹逐渐转变为正向V形裂纹,如图1(c)所示。V形裂纹的产生主要由于3种效应:摩擦拉力效应,环面弯曲效应和弹塑性压痕弯曲效应[17]。由摩擦拉伸和压痕弯曲的影响引起的拉伸应力场倾向于打开垂直于划痕方向的裂纹;划痕凹槽的弯曲效应倾向于打开平行于划痕方向的裂纹。由于这3种效应的影响,进而形成V形裂纹。另外,在划痕凹槽的中心部位观察到横向裂纹,不同于凹槽边缘出现的平行裂纹,且长度较短,在载荷较大时出现。
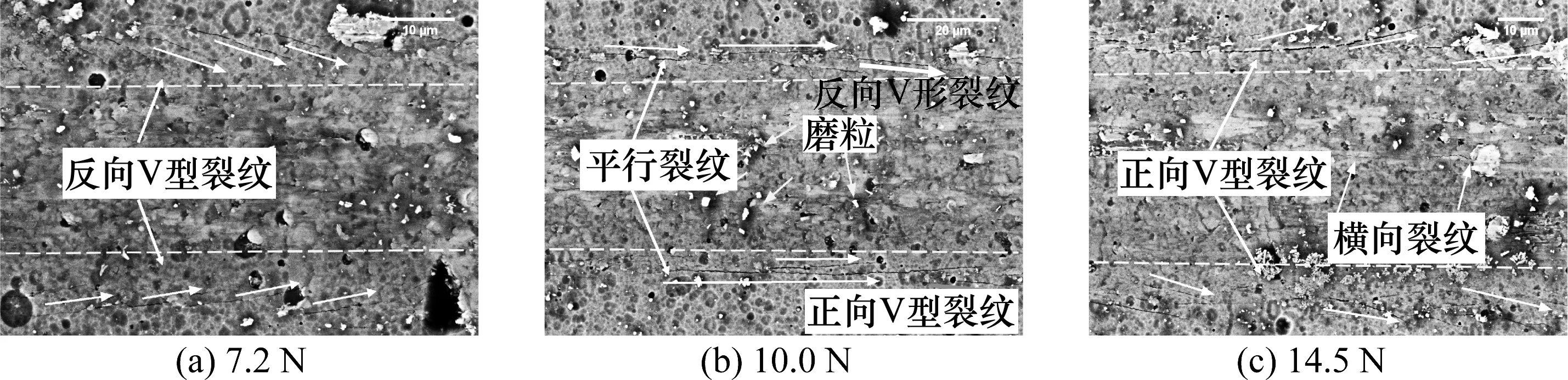
图1 渐进载荷下不同正压力的划痕SEM图像(划痕方向从左到右)
涂层在法向载荷为19 N时发生剥落如图2(a)所示,并出现半圆形裂纹,进入到断裂阶段。粘着失效的发生主要由于金刚石压头前端压缩应力。半圆形裂纹的产生是由于主导应力发生了转变:以压缩应力和局部塑性应力为主导的应力逐渐转变为拉伸应力[15]。由于金刚石压头和涂层表面之间的摩擦力作用,在金刚石压头的前侧产生压缩应力,在金刚石压头的尾部产生拉伸应力,进而导致半圆形裂纹的产生。半圆形裂纹产生的同时伴随着少量的横向裂纹。随着正压力的增加,半圆形裂纹的数量逐渐增加,横向裂纹逐渐消失,如图2(b)所示。横向裂纹的消失主要是由于主导应力发生转变和复杂动态应力场的影响[15,17]。在25 N之前,涂层粘着失效的位置在划痕凹槽的一侧,随着法向载荷的增大,涂层失效的位置逐渐转变到划痕凹槽的两侧,如图2(c)所示。

图2 渐进载荷下不同正压力的划痕SEM图像(划痕方向从左到右)
划痕实验后,使用光学显微镜观察了划痕凹槽形貌,观察到阶梯形的横向条纹,如图3所示。

图3 TiN涂层在渐进载荷12 N左右的划痕形貌光学显微镜照片(划痕方向从左到右)
鉴于TiN涂层柱晶状的微观结构,阶梯形的横向条纹可能是柱晶状TiN之间的剪切滑移。Bhowmick等[18]研究发现涂层塑性变形的发生伴随着TiN晶体之间的剪切开裂。在图4(a)和图4(b)中可以清楚地观察到PVD沉积TiN涂层的柱状晶粒结构,表明阶梯形横向条纹可能是柱晶状TiN晶粒间发生剪切滑移形成的剪切带。在靠近划痕凹槽边缘的位置处观察到许多聚集的柱晶状颗粒,如图4(b)和图4(c)所示。划痕试验中柱晶状TiN颗粒的大量聚集是为了适应大量的剪切应力和犁耕而发生的剪切变形和致密化[16]。在图4(d)中观察到涂层发生阶梯式剥落,类似于在压痕实验中TiN涂层产生的阶梯式边缘裂纹[19]。而且,涂层的阶梯式剥落不会贯穿涂层,涂层剥落的方向与划痕方向相同。同时也观察到位于涂层自由表面下方且与划痕方向呈60°~70°的倾斜裂纹[18]。
在犁耕和界面滑动阶段出现由反向V形裂纹到平行裂纹,再到正向V形裂纹的转变;在断裂阶段半圆形裂纹的出现伴随着横向裂纹。这些失效形式的发生主要是由于动态应力场中多种应力的影响。当金刚石压头在涂层表面滑动时,随着法向载荷的变化会形成复杂的动态应力场[17]。因此,本实验对Larsson[12]绘制的涂层失效形式进行了修正,如图5所示。
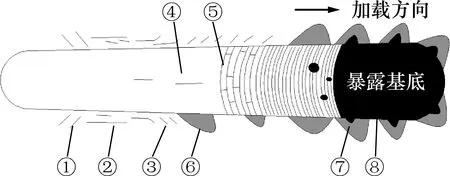
图5 渐进载荷下TiN涂层的失效形式
图6为TiN涂层在渐进载荷加载模式下的划痕曲线。后扫描曲线主要用于评估涂层表面损伤和由于划痕引起的弹塑性变形[17]。当后扫描曲线高于预扫描曲线时,说明涂层发生堆积或划痕过程中划痕凹槽中产生剥落颗粒。
在划痕2.45 mm处,载荷为24.5 N时,后扫描曲线高于预扫描曲线,从图2(b)可以发现划痕凹槽中散落的颗粒,说明划痕凹槽中产生了剥落的TiN颗粒。在划痕曲线的2.9 mm处,载荷为29 N时,后扫描曲线高于预扫描曲线且后扫描曲线平稳增加,相对应的划痕曲线深度不再增加而保持水平,说明涂层发生了堆积,摩擦系数也急剧增加,如图7(b)所示。
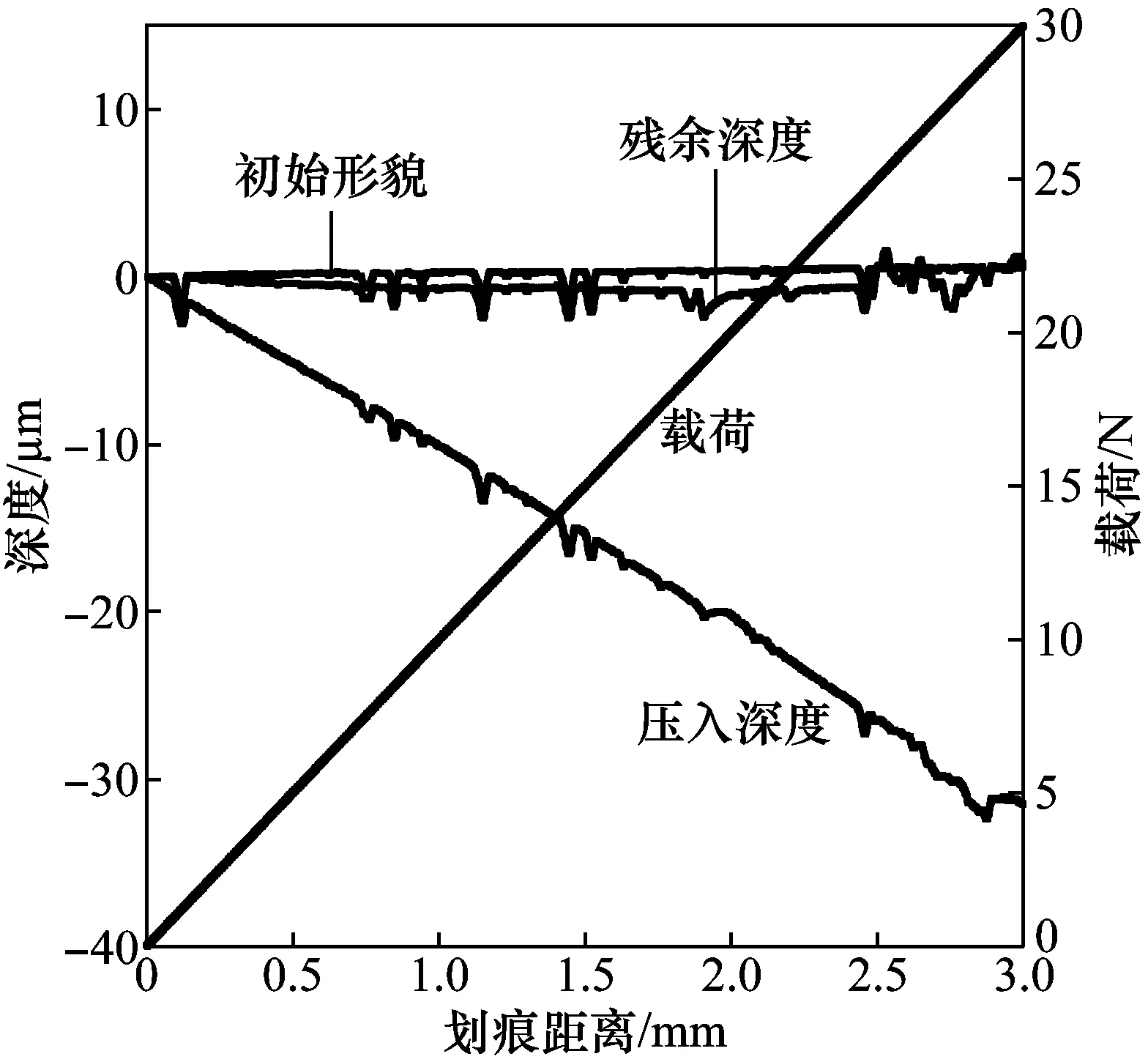
图6 TiN涂层在渐进载荷加载下的划痕曲线
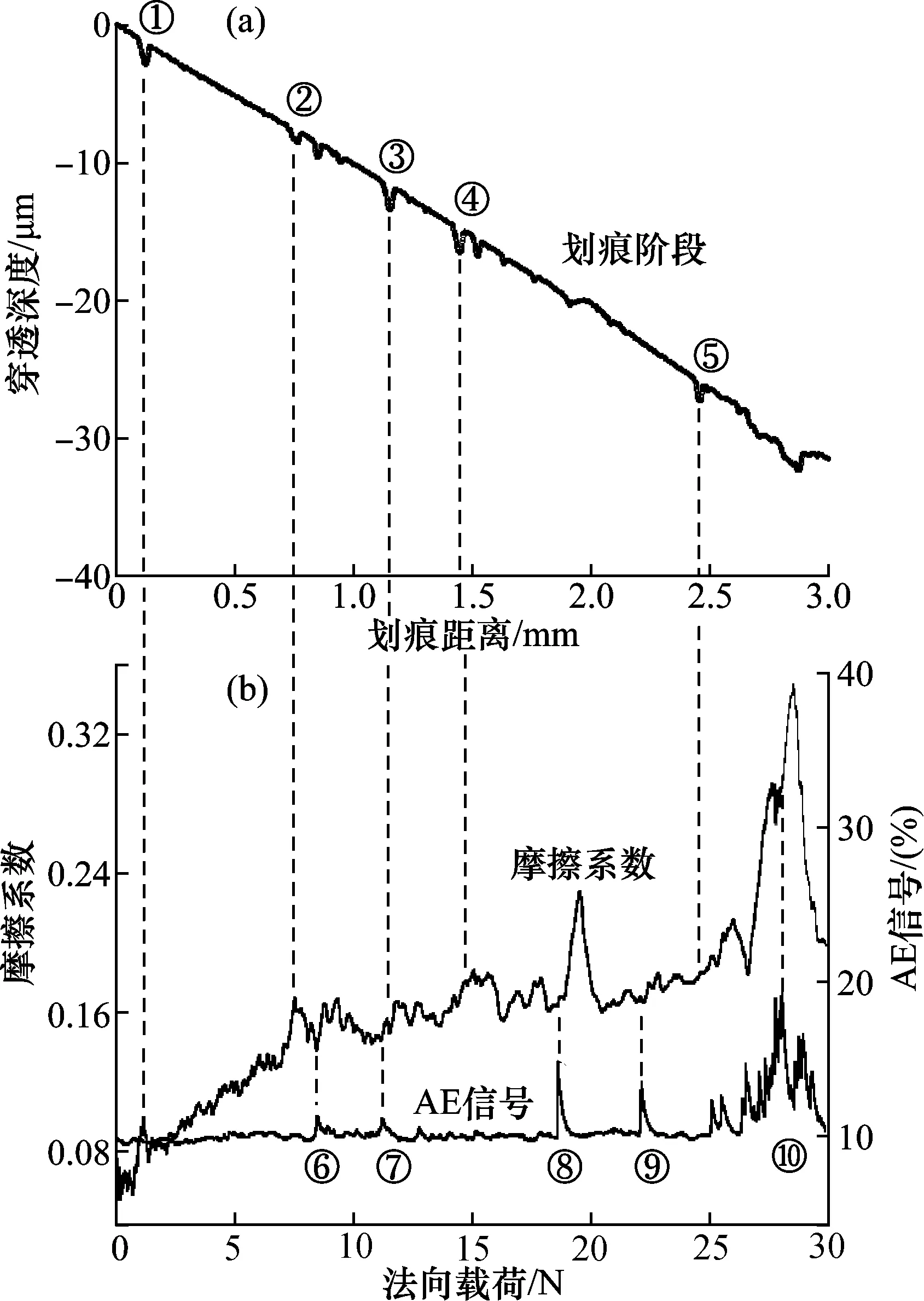
图7 划痕形貌和AE信号与摩擦系数的关系图
划痕实验过程中,金刚石压头尖端的划痕深度是总变形量:包括塑性变形量和弹性回复量(压入深度与残余深度的差值)。
从图8(a)可以看出,在划痕曲线的0.25 mm处,载荷为2.5 N时,初始形貌曲线与残余深度曲线开始分离,说明涂层发生塑性变形。在涂层失效之前,划痕深度随法向载荷的增大而线性增加,不仅与涂层制备的方法有关,而且同一种制备方法不同的加工参数,划痕深度曲线的斜率也不同[20]。在载荷为19 N处,弹塑性变形深度和比例发生突变,如图8中所示。曲线突变处塑性变形深度和比例增加,所对应的摩擦系数也急剧增加,说明涂层发生凹陷,如图2(a)和图7(b)所示。在涂层大量失效之前,塑性变形的深度先缓慢增加后趋于稳定,但是塑性变形所占总变形的比例先增加后缓慢减小,最大比例为12.4%,如图8(b)所示。塑性变形比例的减小,说明弹性变形比例随着深度的增加而增加,TiN涂层具有较高的弹性恢复能力,弹性回复量大于塑性变形量[16]。在载荷为29 N处,弹性变形比例超过100%,与涂层堆积相适应,如图6所示。
如图7(b)所示,法向载荷在到达1 N之前,摩擦系数波动平稳,之后摩擦系数平稳增加。法向载荷到达7 N时,摩擦系数曲线的斜率发生变化。摩擦系数非线性变化的原因主要是由于随着法向载荷的增加,划痕深度超过临界值,压头与涂层表面接触的形状不再是球体[21]。压头是一个半顶角θ=60°的锥体,圆锥的顶端是半径R=100 μm的球体。压头从球体到锥体过渡发生在H=(1-sinθ)R=0.134R=13.4 μm的深度处[22]。在划痕深度小于13.4 μm时,摩擦主要为压头针尖部位的球体与涂层表面接触的摩擦;在划痕深度大于13.4 μm时,摩擦主要为压头锥面部位与涂层之间的摩擦。当法向载荷大于7 N时,摩擦系数出现频繁的波动。摩擦系数的第一次波动发生在点①处,摩擦系数曲线先上升后下降。在点②、③、④和⑤时,也可观察到类似的变化趋势。在点①~⑤处,摩擦系数出现波动的原因主要是表面轮廓发生凹陷,如图7(a)所示。采用白光干涉仪测试涂层的表面粗糙度Ra约为0.06 μm,因此对涂层表面形貌的影响可忽略。压头从表面凹陷的区域向光滑表面滑动时,爬坡会导致切向力的增加,进而导致摩擦系数的值增大。
在8.6 N和11 N处,观察到AE信号出现小的波动,如图7(b)中点⑥和⑦所示。涂层的开裂会使AE信号发生波动,AE信号与划痕过程中裂纹扩展释放的弹性能相对应[23]。同时观察到摩擦系数出现与表面形貌影响相似的波动趋势。在点⑥处,观察到摩擦系数出现类似于M形的波动。可以观察到点⑥处对应的涂层形貌发生凹陷,M形的波动形式可以认为是表面形貌和涂层失效共同作用的结果。在19 N点⑧处,AE信号第一次出现较大的峰值,摩擦系数急剧增加,涂层发生粘着失效,如图2(a)所示。在22 N点⑨处,AE信号出现第二次较大的峰值,涂层发生粘着失效,摩擦系数出现轻微的波动。在26 N之后,在点⑩处,AE信号剧烈波动,涂层发生大面积的剥落,如图2(c)所示,摩擦系数急剧增加。划痕后期,摩擦系数的波动主要是涂层失效的影响,涂层的粘着失效会使摩擦系数急剧增加[24]。
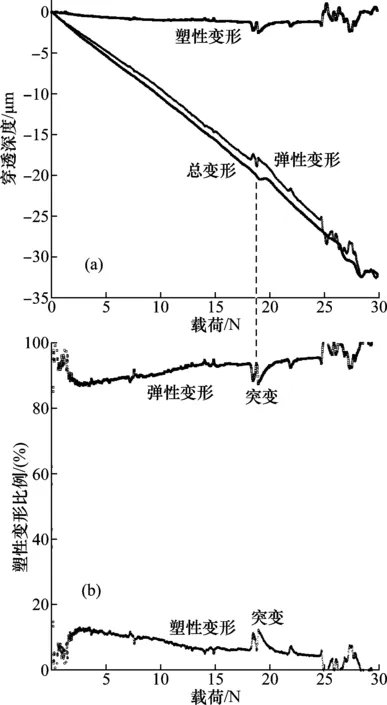
图8 TiN涂层在渐进载荷下的弹塑性变形深度和变形比例与载荷关系
为了比较恒定载荷与渐进载荷测得的摩擦系数是否一致,对样品进行了7 N和13 N的恒定载荷加载(如图9所示),结果表明:恒定加载模式下,摩擦系数的值并没有随着滑动距离的增加而减小[13],相反在7 N时和起始位置相比,摩擦系数会有相应的增加;结束时摩擦系数稳定的数值与渐进加载对应载荷下的数值基本相等。载荷为7 N时,恒定载荷摩擦系数稳定的数值为0.129,渐进载荷摩擦系数的数值为0.131,误差约为1.5%;载荷为13 N时,恒定载荷摩擦系数稳定的数值为0.153,渐进载荷摩擦系数的数值为0.158,误差约为3.2%。取曲线后半段稳定阶段的平均值为恒定载荷的摩擦系数数值。渐进载荷和恒定载荷的摩擦系数数值有较大的差别,说明摩擦系数和加载方式有关。随着法向载荷的增大,摩擦系数的误差增大,与摩擦系数的波动程度随法向载荷增大而增大相适应。
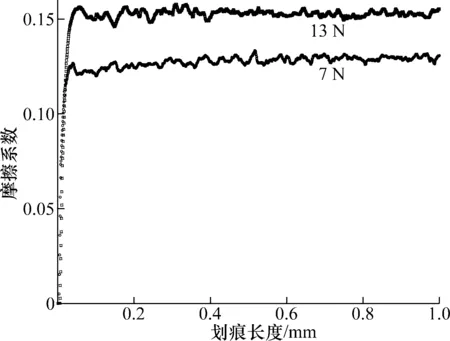
图9 恒定载荷为7 N和13 N的摩擦系数变化图
TiN涂层的断裂韧性采用线弹性断裂力学(LEFM)[22,25]和能量尺寸效应定律(SEL)[26]2种模型进行评估。LEFM模型的断裂韧性Kc可根据式(1)进行评估[22,25]:
(1)
式中:FT为切向力;2pA为压头的形函数,p为压头与材料接触部位在滑动方向上投影的周长,A为压头在滑动方向上承力面的投影面积。
SEL模型是基于尺寸效应定律, 见式(2)[26]所示:
(2)

根据Akono等提出的微观能量尺寸效应定律,可以按照式(3)计算σN和D[26]:
(3)
然后按照式(4)进行拟合:
(4)
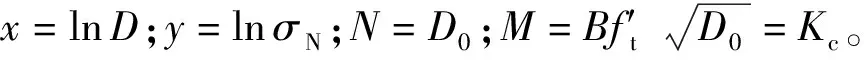
理想的圆锥压头形函数2pA可根据式(5)计入(忽略压头顶端的球体部位)[25]:
2pA=4(tanθ/cosθ)d3
(5)
式中:θ为圆锥半顶角;d为划痕深度。考虑到压头顶端的球体区域对测试的影响不能忽略,对压头的形函数进行了修改。
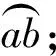
(6)
(7)
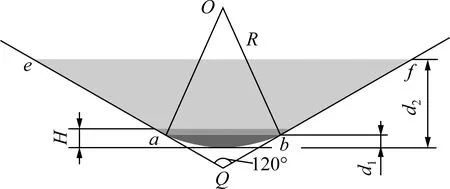
图10 金刚石压头示意图
图11为修正后的形函数和修正前的形函数比值与d/R的关系。在d/R<1时,修正前和修正后的形函数差别较大,对计算结果的影响不能忽略。在d/R>1时,修正后与修正前的形函数比值逐渐减小并趋近于1。因此,在划痕深度较浅的情况下,压头形函数对实验造成的误差不能忽略。
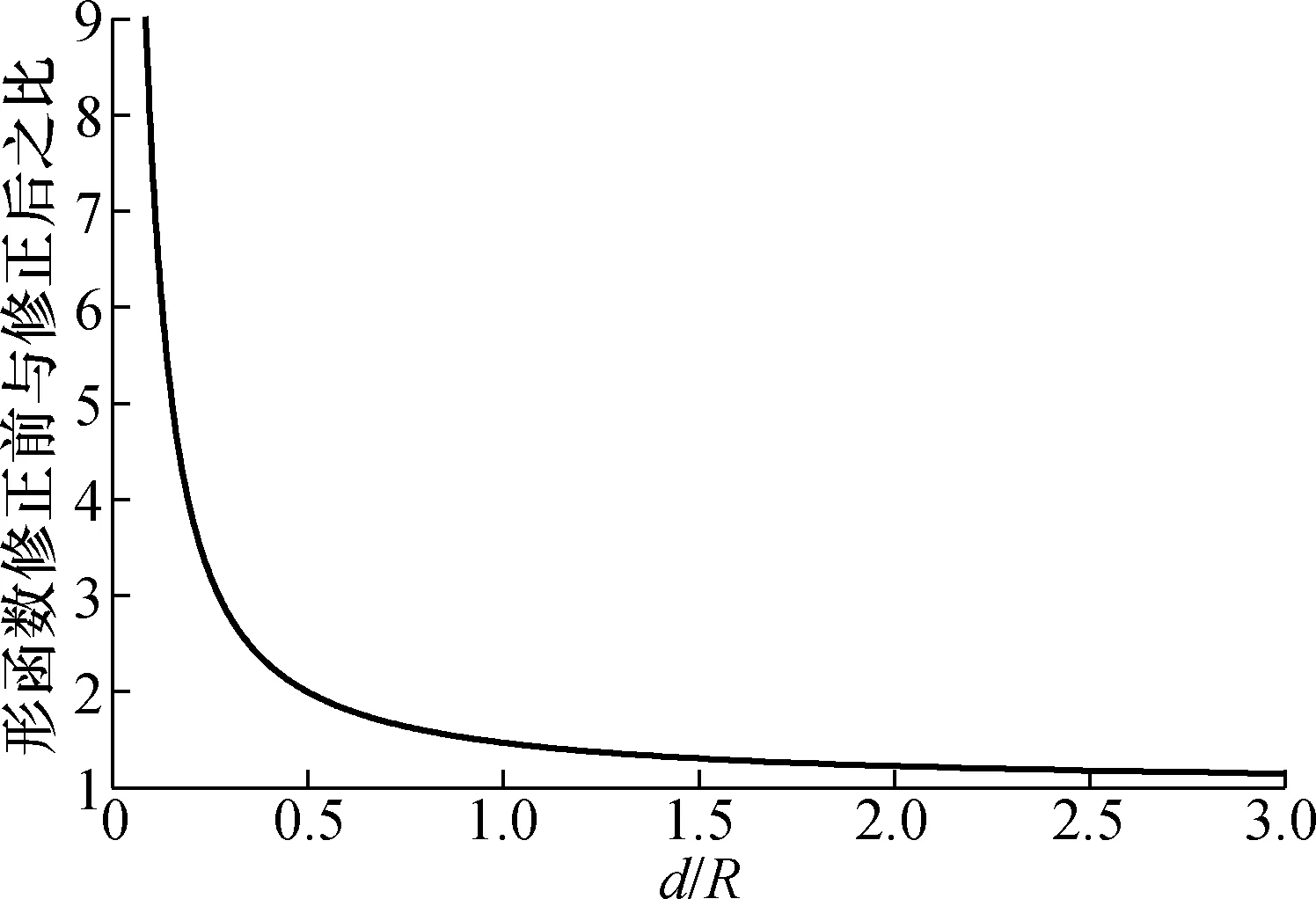
图11 形函数修正前与修正后的比值与d/R的关系
图12为TiN涂层基于LEFM和SEL模型求解的断裂韧性。从图12(a)中可看出形函数修正前的断裂韧性在d/R较小时数值较大(主要由于压头形函数未修正),数值逐渐趋于稳定至9.8 MPa·m1/2左右。形函数修正后的断裂韧性则随着d/R增加而缓慢增加,且断裂阶段的稳定趋势不明显,主要是修正后和修正前的形函数存在差异。
压头形函数修正后的断裂韧性为5.75 MPa·m1/2,接近维氏压头测试的结果5.27 MPa·m1/2[27],并且和SEL模型评估断裂韧性的结果(6.29 MPa·m1/2)相近,如图12(b)所示。测试结果的差异主要由于涂层的厚度不同(文献[27]中TiN涂层的厚度为2 μm),涂层厚度的增加会使涂层内部的残余应力减小,进而导致断裂韧性增大[28]。
Holmberg等[15]采用有限元模型计算TiN涂层的断裂韧性,利用划痕测试中TiN涂层受到的拉应力与裂纹间的距离评估涂层断裂韧性。他们评估TiN涂层的断裂韧性为Kc=7 MPa·m1/2,与形函数修正后测量的数值接近。利用压痕断裂法和有限元模拟方法测试断裂韧性都需要准确测量裂纹的平均长度或距离,因此测量会存在一定的误差。
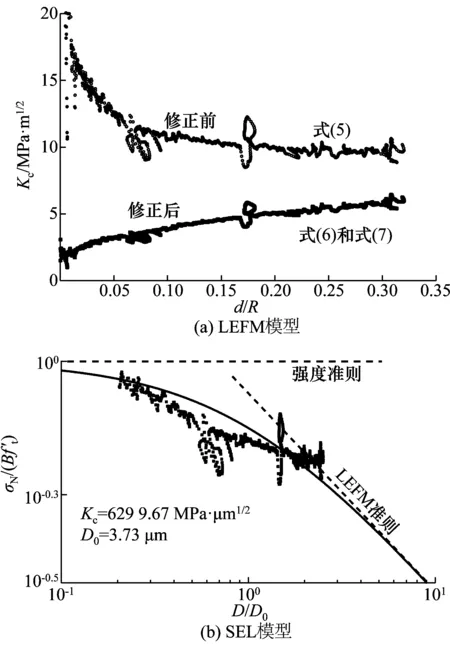
图12 TiN涂层的断裂韧性
4 结 论
通过对TiN涂层的划痕实验,研究了涂层的失效机理,分析了表面形貌和涂层失效对摩擦系数的影响,并评估了断裂韧性。主要的结论如下:
1)TiN涂层出现了由反向V形裂纹到平行裂纹,再到正向V形裂纹的新转变形式,与先前众多学者研究TiN涂层的失效形式不同,还需要深入的研究。
2)表面不光滑和涂层剥落是影响摩擦系数波动的主要因素,进而可通过摩擦系数的波动情况推导出表面形貌和失效形式,具有一定的指导意义。
3)采用微米划痕可以较准确地测试TiN涂层的断裂韧性,相比其它测试断裂韧性的方法(如压痕断裂法等),操作简单,对样品要求不严格,具有较高的实用价值。
