基于改进Sierra 抖动算法的微离焦投影三维轮廓测量技术研究

魏小华，徐文俊，徐雪雅

(1.衢州职业技术学院 机电工程学院，浙江 衢州 324000；2.杭州电子科技大学 机械工程学院，浙江 杭州 310018)

1 引 言

数字光处理(digital light procession，DLP)技术由于其灵活性，已应用于非接触式的光学测量来对待测物进行三维的轮廓重建[1]。传统DLP技术利用计算机生成正弦光栅进一步发送到投影仪，由于它通常需要8位表示一个正弦光栅，测量速度通常限制在120 Hz(投影仪刷新频率)[2];此外，由于大多数商用投影仪是非线性，在投影仪没有非线性补偿的情况下，会引入额外的测量误差，且电荷耦合器件(CCD)采集的光栅图像不具备良好的正弦性[3]。为解决传统DLP技术带来的问题，二值光栅离焦测量技术被提出[4]，它所能达到的测量速度及正弦性均进一步提高[5]，由于投影仪接受的不是灰度图而是二值图像，当投影仪处于离焦状态时，就可以投影出具备良好正弦性的光栅图。然而，由于二值光栅存在高频谐波，测量准确性受到极大的影响。脉冲宽度调制(pulse width modulation，PWM)技术本质上调节二进制模式的高频谐波，可以更容易得到抑制，或消除离焦，但是PWM技术往往适用于处理窄条纹的二值光栅，在光栅条纹较宽的条件下，结果不是很理想。基于面积编码的二值化算法，李平平等[6]提出了进一步的改进，即在对二值化模板进行填充时，用分散的、尽可能等间距的填充方法代替分块的、非等间隔的填充方法，并将此光栅制作出来用于三维形貌测量。田紫霞等[7]利用误差扩散方法产生二元编码正弦光栅，并针对该编码正弦光栅较差的正弦性，提出了两种改进技术；Ayubi G A等[8]提出一个正弦条纹生成技术，即正弦脉宽调制(sinusoidal pulse width modulation，SPWM)，利用微离焦二进制边缘投影，鉴于使用现成的投影仪SPWM很容易实现，该方法可以克服投影仪的Gamma畸变效应；Wang Y等[9]提出的二进制离焦技术来人工纹理和细节丢失的问题，仿真和实验结果表明相位误差低于0.6%；Dai J F等[10]提出Bayer-dithering技术为可以大幅度提高3D测量质量的二进制离焦方法；文献[11，12]分析了Floyd-steinberg dithering算法误差扩散非对称性对离焦正弦结构光投影误差的影响，使用平行于条纹方向扫描的Floyd-steinberg dithering算法将使离焦结构光图像在不同离焦状态、不同相移步数情况下的相位提取结果更加一致、误差更小；Ghorayeb S R等[13]利用最优脉宽调制(optimal pulse width modulation，OPWM)和基于Stucki抖动算法来生成光栅条纹，从而实现动态三维轮廓测量，但Stucki误差扩散抖动算法的计算过程较为复杂。

以上几种方法虽能生成高质量的正弦光栅条纹，但测量速度和精度仍有提高的空间。在三维轮廓测量过程中，光栅条纹的正弦性直接会影响相位测量的精度，因此，为降低高次谐波的影响、抑制投影仪非线性Gamma效应及提高测量效率等，提出基于蛇形扫描的改进Sierra抖动算法，该算法既能够显著提高光栅的质量，又具备更好的正弦性。同时，在投影仪处于微离焦状态下，与Bayer有序抖动算法、Sierra抖动算法和Floyd-Steinberg误差扩散抖动算法等比较，实验结果均表明：基于投影系统微离焦的改进Sierra抖动算法具备更好的适应性，能够更大程度地提高测量速度，降低相位误差，提高光栅投影三维轮廓测量精度。

2 算法基本原理

2.1 相移算法

图1 测量系统原理图

图1为测量系统原理图。由投影仪投射出条纹图案至待测物体表面，接着由CCD摄影系统获取影像，而投影仪与CCD摄像系统中心距离为d，数字投影仪光心或摄像系统(CCD)光心到参考面距离l。由于光栅的条纹被凹凸不平的物体表面所调制，使得原本A点相位移动到C点，相移值为φ(x，y)。设光栅频率为f0，周期为p，则φ(x，y)=2πf0|AC|。由于受到光栅调制发生形变，以此方式扩张成整个投影面则会发现原本的直条纹产生了扭曲，由CCD摄像系统获取的变形光栅可写为

I(x，y)=A(x，y)+B(x，y)cos[φ(x，y)+kπ/2]

(1)

式中：I(x，y)表示摄像机接收到的光强值；A(x，y)表示投射光场中缓慢变化的背景分量；B(x，y)表示条纹幅度；f0表示光栅条纹频率；φ(x，y)是表示相位变化值；k表示第k帧条纹图(k=0，l，…，k-1)，即光栅每次移动1/k周期，条纹相位被移动2π/k。假设光场分布为Ik(x，y)，用3个或者更多不同相移值光场分布条纹图，求得物面上的相位分布[14]可表示为：

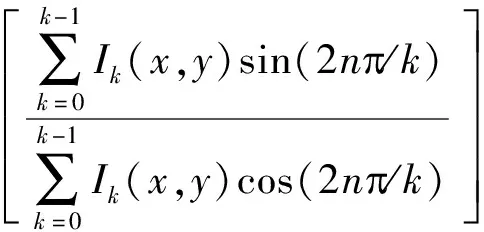
(2)

由式(2)计算获取不连续的相位分布φ(x，y)，即±kπ(k=1，2，…)处不连续，使用去包裹算法[15]可以恢复原来连续分布相位φ(x，y)。根据相似三角形关系可得相位和高度的转换式，来得到物体的三维轮廓，其高度计算式表示为

(3)

2.2 抖动算法

图像抖动算法是将正弦光栅经算法处理生成的二值抖动光栅，二值抖动光栅经过投影仪离焦投射到被测物体表面，从而实现离焦光栅投影测量。误差扩散抖动法的基本思想是将原始灰度图像的当前像素值与固定阈值相比较，一般情况下，选取最大灰度值的一半作为阈值，得到一个二值输出，然后将输入与输出的像素值差以一定的方式扩散到未经处理的邻近区域，图2为误差扩散算法原理图。图2中，Q[*]表示阈值量化器；g(m，n)为原灰度图像；e(m，n)为量化误差，即u(m，n)-b(m，n)；w(k，l)为误差扩散系数，误差扩散算法所对应的数学模型为

(4)

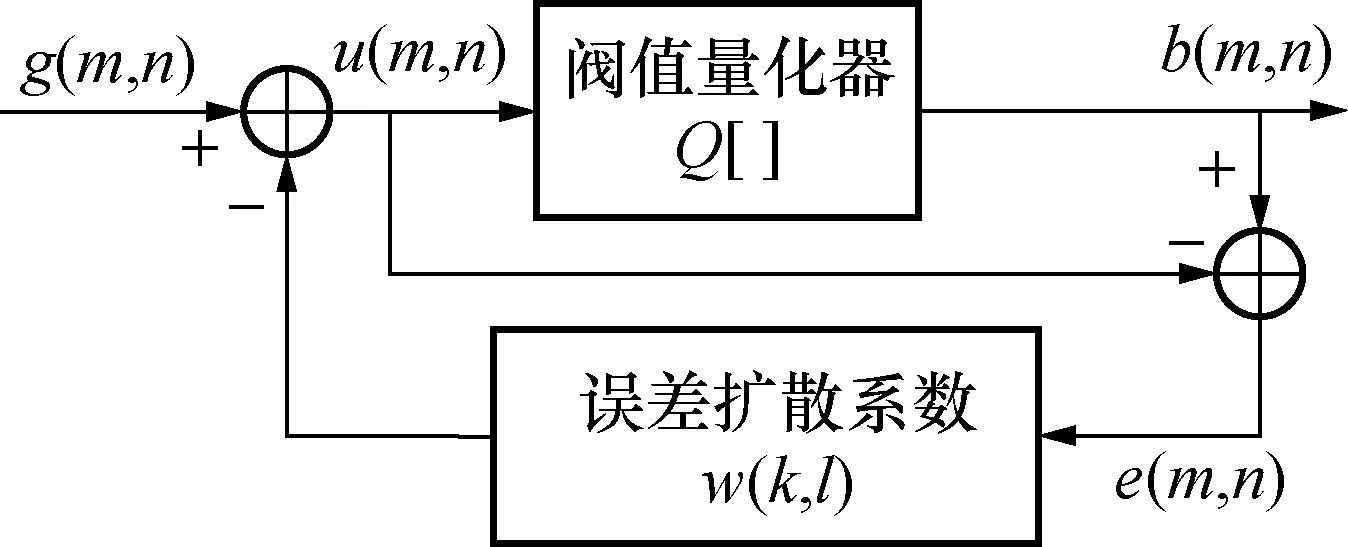
图2 误差扩散算法原理图

根据阈值κ=128，将u(m，n)像素二值化，最终获得抖动图像像素b(m，n)，即：

(5)

(6)

由上述公式可以发现，当前像素量化误差u(m，n)不仅由当前位置输入输出像素值决定，同时也依赖于已处理区域像素对当前像素的影响，误差扩散法实质上也是一种基于区域的半色调算法，扫描顺序(或扫描路径)也是影响半色调图像质量一个因素，重复以上过程，逐行处理，最终获取二值抖动图像。

2.3 改进的抖动算法

核函数w(k，l)是各种误差扩散中的关键参数及区别所在，它是误差扩散中最重要的参数。其中，对于Sierra抖动算法，其核函数为

(7)

式中：“-”表示已处理过的像素；“*”表示当前正在处理的像素；误差扩散核函数矩阵中右边紧邻像素获得1/2的权重，正下方像素获得1/4的权重，左下角像素获得1/4的权重。

由于传统的误差扩散为从左到右、从上往下计算，误差在扩散时会引起误差累积，影响抖动图像的质量。因此，本文提出一种改进Sierra抖动算法(简称：改进Sierra算法)，基于蛇形扫描，即奇数行从左向右扫描，偶数行从右向左扫描，则偶数行的误差扩散核函数为

(8)

式中：偶数行的误差扩散核函数矩阵中右边紧邻像素获得1/2的权重，正下方像素获得1/4的权重，右下角像素获得1/4的权重。

采用改进Sierra算法误差扩散过程如图3所示，其中α、β和γ为误差扩散系数，即核函数中所对应的参数值α=1/4、β=1/4和γ=1/4。

图3 蛇形扫描和误差扩散原理图

通过理论分析可知，该算法避免将误差传递给下一级周围的像素，因此基于改进算法的抖动图像具备更好的对称性和更高的图像质量。为更清楚且直观表达两种抖动算法的光栅图，如图4所示为基于Sierra误差扩散抖动离焦前后光栅条纹图，图5给出了基于improved Sierra误差扩散抖动离焦前后光栅条纹图。

图4 Sierra误差扩散抖动条纹图

图5 Improved Sierra误差扩散抖动条纹图

为了进一步描述4种抖动算法生成光栅的正弦性，基于低通滤波器模拟微离焦投影，取微离焦光栅图中的某一行，并且与标准的正弦光栅图某行截面曲线进行比较，结果如图6所示。

由图6可知：Bayer抖动生成正弦性较差，Floyd-steinberg和Sierra抖动生成正弦与标准正弦有明显偏差，而Improved Sierra抖动生成正弦性最好，质量较高。

图6 正弦与标准正弦曲线结果比较

通过仿真实验，进一步分析Improved Sierra误差扩散抖动算法在相位测量中的精度，与典型的3种误差抖动算法做比较。图7所示为基于不同条件下的均方根(RMS)误差比较结果。

图7 基于不同条件下的RMS误差比较

图7(a)为不同相位移动步数(S=3，4，5，…)误差图，周期T=50 pixel，高斯滤波器f=15 pixel，由该数据分析可知，4种算法的相位误差随步数增加，减少十分微弱，且误差基本趋于稳定，这是由于抖动后的条纹具有相当稳定的正弦性；图7(b)为不同条纹周期下的相位误差比较图，相移S=3，高斯滤波器f=15 pixel，4种算法的相位误差随着周期的增加而减少；图7(c)和图7(d)分别为不同离焦程度的相位误差比较图和不同离焦度亮度误差比较图，相移S=3步，周期T=50 pixel，可以看出，4种算法都在离焦度合适时才具备更小的相位误差，且亮度误差和相位误差一致的。从图7中的4幅图可得出，与其它常用的有序抖动算法相比，采用Improved Sierra误差扩散抖动算法所获得的正弦光栅条纹的相位误差均小于其它3种误差扩散抖动算法，Improved Sierra抖动图像的质量更好，基于适度离焦状态，更加适合物体三维轮廓测量。

3 实验分析

该测量系统包括一个DLP投影仪和CCD(JaiPulnixtm-6740-cl)。相机连接于一个16 mm焦距像素镜头(Computar M1614-MP)。相机的分辨率640 pixel×480 pixel，和投影仪分辨率为800 pixel×600 pixel，投影距离为0.49 ～2.80 m，周期T=50 pixel，高斯滤波器f=15 pixel。以白板为参考平面，测量并计算相对相位误差，由于在投影仪充分离焦状态下，二值化光栅和标准正弦光栅的投影效果趋于一致，因此实验基于投影仪轻微离焦状态。图8为基于Improved Sierra离焦光栅测量结果，图8(a)为相机采集到的周期为100 pixel的离焦投影图；图8(b)为包裹相位图；图8(c)为未去包裹的第220行相位图；如图8(d)为去包裹相位图。由于微离焦的抖动光栅正弦性更好，致使获得更高质量的相位。

图8 基于Improved Sierra离焦光栅测量结果

同时，在投影仪离焦程度较低的情况下，测量并计算了Improved Sierra抖动算法生成的不同周期光栅的相位误差，与Bayer、Floyd-steinberg、Sierra等几种算法进行了比较[16～18]，如图9所示。可以看出，该实验与理论分析结果相一致，改进Sierra抖动算法无论在条纹周期较小还是条纹周期较大的时刻均可以保持较低的相位误差。

为了进一步计算相对相位误差，利用该实验装置对曲面更加复杂的心形石膏模型进行三维重建，调整投影仪处于轻微离焦状态，分别使用典型Bayer、Floyd-steinberg、Sierra及Improved Sierra抖动光栅进行三维重建结果，如图10所示。

图9 不同周期下的相位误差比较

图10 基于微离焦投影技术的三维重建结果

采用RMS误差σ来评判测量精度：

(9)

式中：Hr(x，y)为三坐标测量的真值；Hm(x，y)为观测值；m为观测数。

采集图10中4种方法获取的三维物体第160～167行数据，计算σ如表1所示，抽取观测数m=50，本文提出基于蛇形扫描改进Sierra抖动算法的σ总体略小于其它算法；实验表明该算法具有较高的测量精度。

表1 4种算法的σ比较

Tab.1 Comparison ofσusing four kinds of algorithms mm

组别BayerFloyd-steinbergSierraImprovedSierra10.02790.01560.01520.014120.03850.02270.01970.017530.02960.01290.01130.010940.03270.02240.01930.012150.02280.02190.01530.013760.02060.02450.01430.015870.02270.01240.01930.002180.02630.02190.02820.0164

表2为4种算法的运算时间比较，Improved Sierra抖动算法与其它3种算法比较，运行速度最快。

表2 4种算法的运算时间比较

Tab.2 Comparison of operation time of 4 algorithms s

序号算法时间1Bayer4.2382Floyd-steinberg3.9073Sierra2.9364改进Sierra2.715

4 结 论

本文提出基于蛇形扫描改进Sierra抖动算法获取的投影光栅，能够显著提高光栅的质量，具有更好的正弦性。在投影仪适度离焦时，与Bayer有序抖动算法、Sierra抖动算法和Floyd-steinberg误差扩散抖动算法相比，仿真及实验结果均表明：基于微离焦投影的改进Sierra抖动算法具备更好的适应性，抖动光栅由于不受非线性影响，既能保持相移轮廓术至少需要3幅畸变光栅就可以获取相位的特点，且降低了误差，运算速度快，从而改善光栅投影三维轮廓测量精度。