一种单频激光干涉仪非线性误差修正方法研究

金 涛，唐一揆，乐燕芬，刘芳芳，雷李华

(1.上海理工大学 光电信息与计算机工程学院，上海 200093；2.上海市计量测试技术研究院，上海 201203)

1 引 言

随着现代工业技术的不断进步，工业加工制造业和科学研究对精密测量的要求越来越高，众多测量物理量中，长度是最基本的测量对象之一。激光干涉由于测量分辨力高，测量结果可直接溯源被广泛应用到长度相关的测量中[1]。然而，无论双频干涉仪还是单频干涉仪均存在非线性误差[2，3]。该误差限制了干涉仪的测量精度，因此对非线性误差修正和补偿是激光干涉仪研究的重点和热点。

单频激光干涉仪非线性误差修正的方法有很多，其中研究最多的是基于正交干涉信号的相位补偿法。1981年，Heydemann首次提出了正交干涉信号的相位误差修正模型[4]，使用最小二乘法的非线性拟合方式消除非线性误差;Wu和Eom对单频干涉仪非线性误差进行了详细的分析，非线性误差是由光源和光学元件的性能以及干涉仪调整误差等原因引起，反应到信号中即为干涉信号幅度不等、相位非正交和直流偏移引起的相位计算的误差[5];黎永前等提出了混频谐波分析法，对两路干涉信号进行谐波分析得到幅度比、相位差和直流偏置并进行非线性误差修正,该方法精度高，数学运算相对复杂[6～8];卢明臻等提出了一种谐波分离的修正方法，在最小二乘法的基础上，引入了傅里叶级数，进一步消除了非线性误差中的各种谐波成分[9];胡红波等通过对直流与幅度整形操作基本消除幅度不一致与零漂两个参数的影响，再通过最小二乘法实现对正交干涉信号非线性误差进行修正[10，11];胡鹏程等人用渥拉斯特棱角巧妙地抑制了由于消光比引入的偏振态混叠，并通过两两相互正交的信号的四路干涉信号实现任意直流偏置情况下的非线性修正[12];Köning等为解决最小二乘法Heydemann修正无法评估修正误差问题，提出了基于几何距离最小的正交干涉相位补偿方法[13]。

本文研究了几何距离的计算模型，利用英国国家物理实验室(NPL)的Jamin干涉仪和德国PI(S-310k002)的纳米位移台搭建了验证性实验。所用Jamin干涉仪通过X-ray干涉仪标定后非线性误差最大不高于800 pm，最小可以达到40 pm[14]。通过与Jamin干涉仪和纳米位移台的电容式传感器的位移进行比较，实验结果显示，基于几何距离最小的修正算法的修正精度高于NPL的Jamin干涉仪的解算结果。

2 Jamin干涉仪测量原理

Jamin差分平面镜干涉仪(DPMI)由偏振分光板(PSP)、偏振分光棱镜(PBS)、1/4波片、直角棱镜和反光镜组成，其光路结构如图1所示。

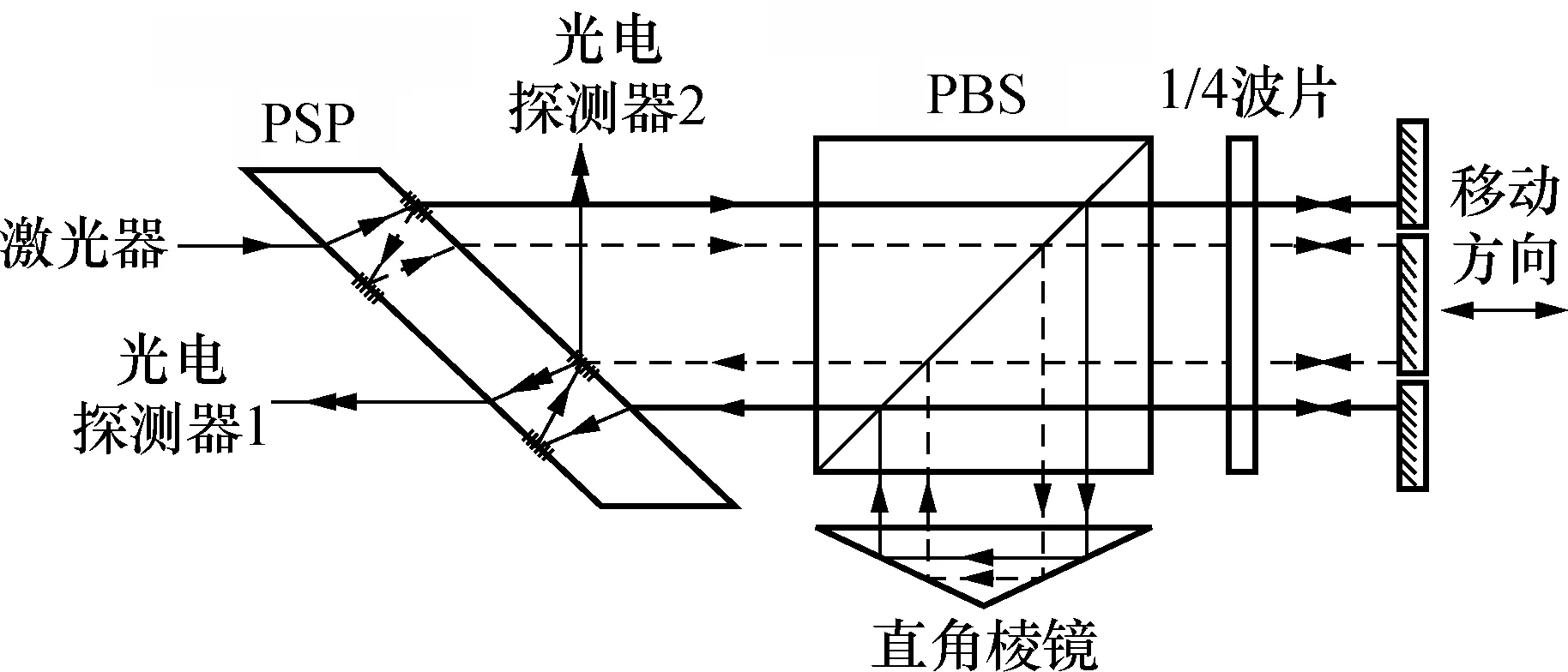
图1 基于差分平面镜的Jamin干涉仪测量光路结构图

氦氖激光器发出的线偏振光(P光)射入PSP，经过镀在PSP表面反射透射率为50%的半反膜后，被分为能量相同的两束光线。一束光(图中用实线表示)直接透射通过PSP表面的分光膜，另一束光(图中用虚线表示)经两次反射后从另一光路透射出PSP。这两束P光射入PBS后，直接透射通过偏振分光膜，在两次通过1/4波片后，振动方向改变了90°，偏振态发生改变，由P光转变为S光，并由反射镜原路反射回PBS，S光被偏振分光膜反射，垂直入射直角棱镜，经两个直角面反射后，射向偏振分光膜并被反射。两束S光，再次通过1/4波片和反射镜，偏振态发生改变，转变回P光，并射回PSP，镀在PSP表面的偏振膜将引入90°的相位差，得到光强相近的正弦和余弦干涉信号，两个光电探测器分别接收探测正弦和余弦信号。这两路信号经过信号处理后用于位移测量和非线性误差修正。基于差分平面镜结构的Jamin干涉仪具有结构紧凑、共光路、光学分辨率高的特点。

3 基于几何距离的Heydemann修正

如图1所示，光电探测器接收到的相位相差90°的两路干涉信息，其数学表达式可以定义为：

x(t)=α0+α1cosφ(t)+εx

y(t)=β0+β1sin[φ(t)+φ0]+εy

(1)

式中：α0和β0为椭圆中心坐标；α1和β1为信号的振幅；εx和εy为满足高斯分布且相互独立的随机噪声，其数学期望为0；φ0表示初始相位；φ(t)是由于光程变化(当被测物体移动时)引起的相位变化。通过式(1)可计算出φ(t)如式(2)所示：

(2)

显然，为了计算φ,需要确定式(2)中的5个参数α0，α1，β0，β1，φ0。根据经典的Heydemann修正理论模型[4]，将相互正交的两路信号分别作为X和Y可以绘制出一个圆或椭圆。输入至示波器的将椭圆轨迹方程表示为：

F(x，y;γ)=Ax2+Bxy+Cy2+Dx+Ey+F

γ=(A，B，C，D，E，F)

(3)

式中：γ=(A，B，C，D，E，F)为椭圆参数矢量。在此模型上改进的几何距离最小化计算理论模型，能够引入更多参数信息，因此可以进一步提高测量精度，实现高效稳定的测量目的。忽略测量误差和干扰因素的影响，式(1)可以简化为[14]：

μs=α0+α1cosφ

νs=β0+β1sin(φ+φ0)

(4)

式中：μs和νs表示理想条件下的正交干涉信号。同理，式(3)也可转化为：

(5)

李萨如图形受2n+5个参数的非线性约束，因此需要对参数的计算进一步简化，从而使计算步骤更加高效，其简化结果如下：

(6)

一旦椭圆参数矢量θ=(B，C，D，F，G)确定，那么将式(6)中的5个参数代入到式(2)中，即可推算得出干涉相位φ的值。

以预估参数μ0，ν0，θ0的一阶泰勒展开式为条件，线性化非线性约束条件Bθ+b=0，可以得到：

Bθ+b=A0(

μΔ

νΔ

)+B0θΔ+c0

A0=[Diag((0⋮ν0⋮1⋮0⋮0)θ0+2μ0)⋮

Diag((2ν0⋮μ0⋮0⋮1⋮0)θ0)]

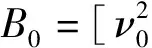
μΔ=μ-μ0，νΔ=ν-ν0，θΔ=θ-θ0，

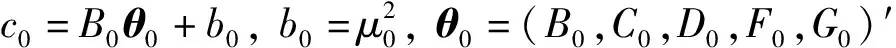
(7)

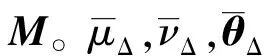
(8)

(9)

式中：Qxy，0表示矩阵Q0第x行第y列的分块矩阵。之后，进行几何距离最小化的循环迭代算法[15]，具体步骤如下：

(1)设置初始值

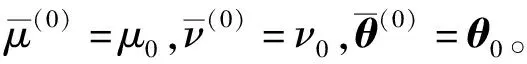
(2)判别收敛性

检验收敛性判别依据是否成立：crit<εtol或k≥kmax，若成立，则终止迭代算法，反之，则进入步骤3。

(3)线性化

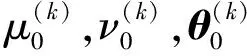
(10)

(4)预估参数值

由式(7)所得的线性化约束条件Bθ+b=0，建立含线性约束的一阶近似线性回归模型，作为迭代修正估值的约束条件，如式(11)所示：

(11)

式中：xΔ=x-μ0，yΔ=y-ν0，再根据式(7)与式(10)，对信号参数值进行迭代估值：

(12)

(5)更新判别函数值

(13)

更新迭代次数k=k+1，并重新回到步骤(2)进行计算处理。

最终，当迭代结束时，该算法将输出信号参数的预估值，如式(14)所示：

(14)

通过计算得到式(14)中3个信号参数的预估值，即可得到椭圆参数矢量θ=(B，C，D，F，G)的确定值，代入式(2)中后，计算得到相应的干涉相位φ，从而实现相位的修正与李萨如图形的拟合。

4 实验结果与分析

在压电陶瓷驱动电压为1、2、5 V时，分别采集了Jamin干涉仪输出的相应的正交干涉信号。

根据改进后的基于几何距离最小化的Heydemann修正计算理论模型，在Matlab中对该修正模型的数学算法进行仿真实验，并对二次曲线进行平滑处理，得到了修正后的图形。

图2(a)显示了驱动电压为1 V时采集的李萨如图形、本文修正算法修正的干涉圆和Jamin干涉仪修正的干涉圆。修正后的干涉圆与Jamin干涉仪的干涉圆几乎重合，结果相近。

图2(b)表示了两种方法修正后的干涉圆的半径偏差。该偏差为周期变化，表明了两种修正算法在所有点的修正结果不完全相同，偏差的平均值为3.41 mV，约占干涉仪圆半径的3‰，偏差的峰-峰值约为0.1 mV，仅为干涉仪半径的万分之一。

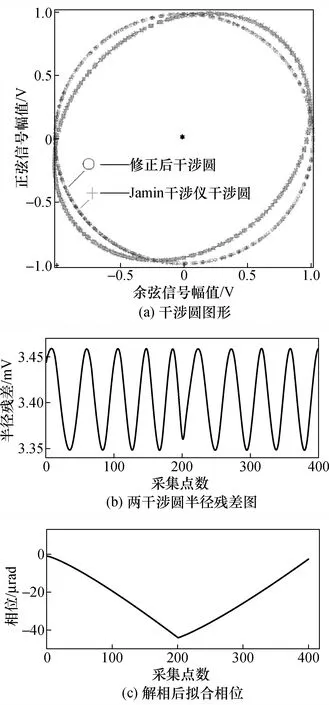
图2 修正李萨如图形及解相后拟合相位(1 V)

说明两种修正算法得到的干涉圆非常接近，验证了修正算法的有效性。由于正切函数在其每个周期节点[-π/2，π/2]会产生跳变，在进行反正切计算后将导致拟合相位函数变为间断函数，因此需要对拟合相位进行解相，使其由间断函数变为连续函数，解相后的拟合相位结果如图2(c)所示。

图3是驱动电压为1、2、5 V条件下的修正位移-理论位移图，用以校准修正后位移的精确度，验证几何距离最小化计算模型下的修正准确性与稳定性。采样点数同为401个，位移台往返运动1次，位移台位移行程随电压增大而增大，通过计算不同位移行程下的修正后位移-电压函数斜率，能够发现，这些一次函数的斜率几乎相同，约为-1.000 0，同样的，不同位移行程下的修正位移-Jamin干涉仪解算位移曲线的斜率也看作几乎相等。说明基于几何距离最小化计算模型的拟合结果能够保证较高的测量精度，可适应纳米级别的测量需求，且算法表现出有较强的适用性与稳定性。

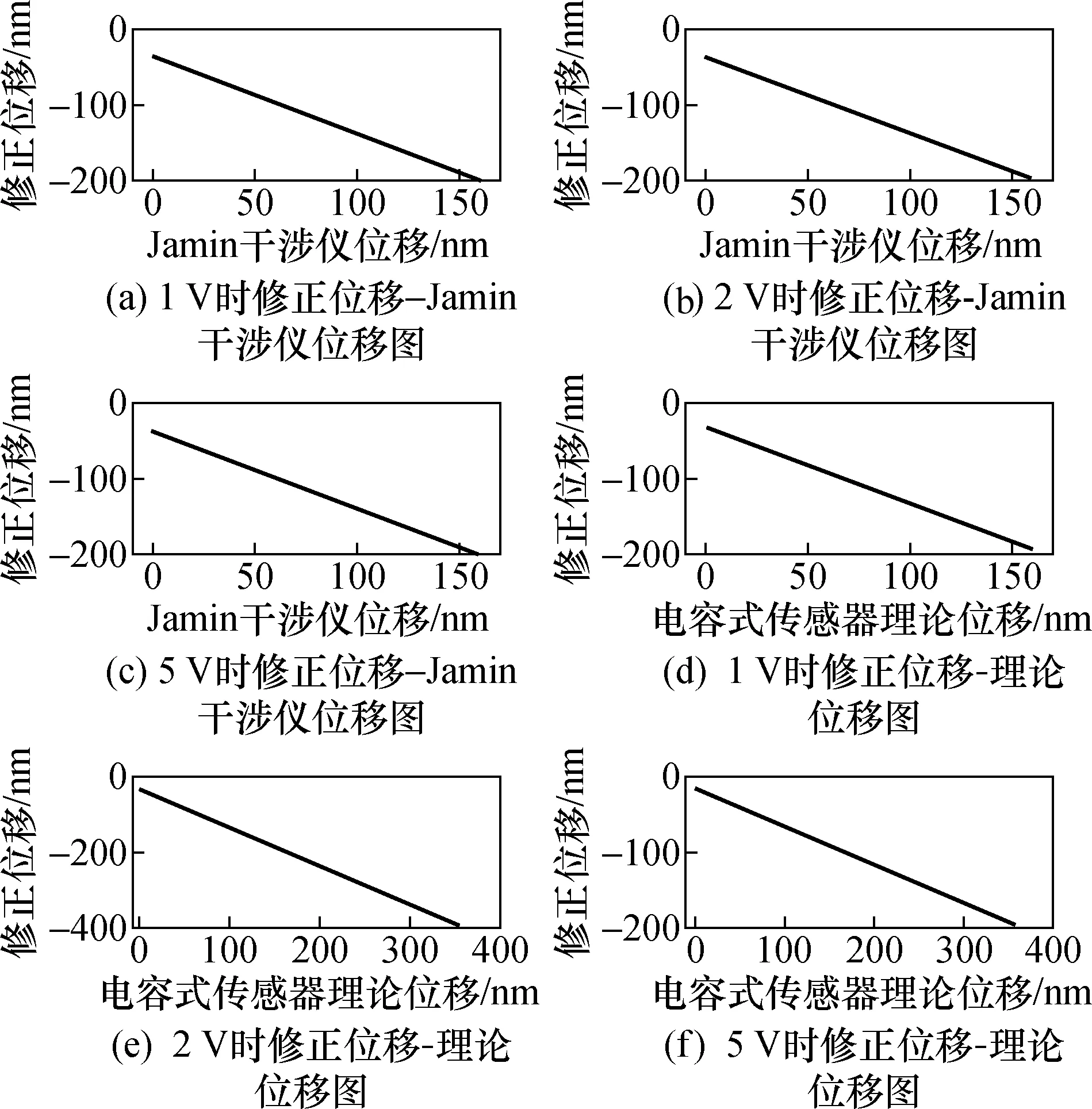
图3 拟合位移校准图

修正后位移曲线的拟合优度分析如表1所示。由于压电陶瓷存在迟滞效应，因此应分别计算位移台去程与回程时的相关参数。

结果表明，拟合优度与Jamin干涉仪数据基本相同。在1、2、5 V这3种不同电压条件时，相同去回程下的修正后位移曲线与Jamin干涉仪解算结果曲线的斜率偏差为1×10-3，去程与回程的修正后位移曲线的决定系数R2基本保持稳定，近似约等于1，且其标准差较小，显示出修正算法的稳定性较强，拟合优度较好[15，16]。

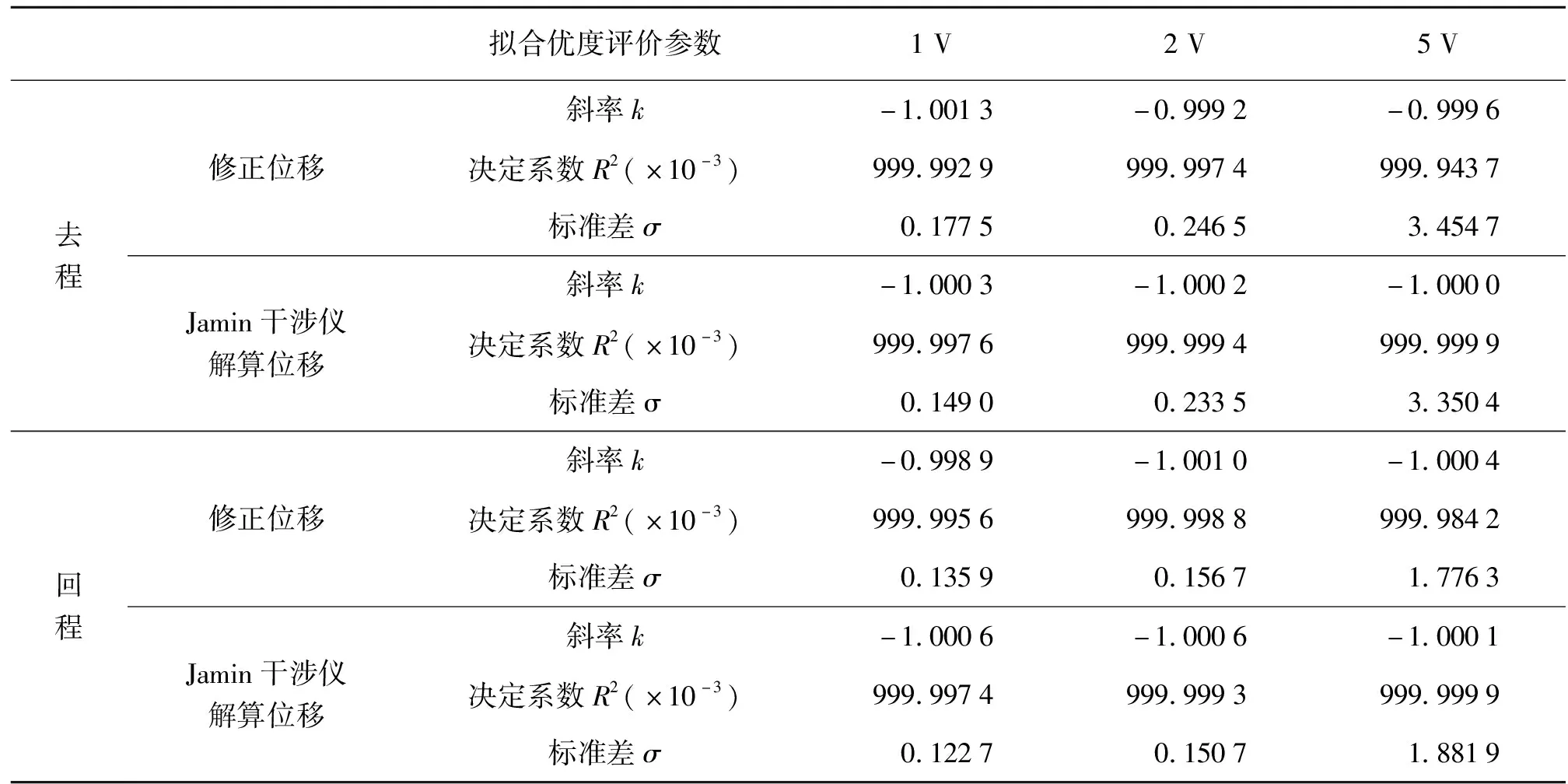
表1 修正后的位移曲线拟合优度检验表

为了进一步验证修正结果的准确性，可根据电容式传感器的灵敏系数与电压值，换算得出相同条件下纳米位移台的理论位移量，绘制出修正后位移、Jamin干涉仪与纳米位移台电容式传感器理论位移值的残差曲线图，如图4所示。

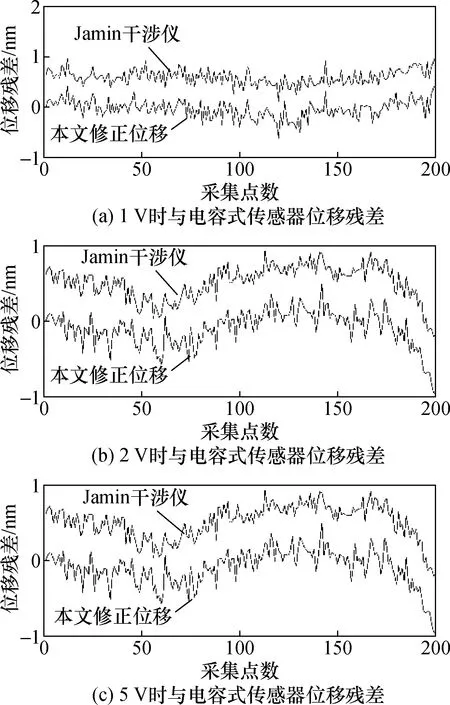
图4 修正位移和Jamin干涉仪与电容式传感器残差对比图

由图4中的曲线对比可知，经基于几何距离最小化的Heydemann修正算法修正后的位移曲线更接近位移台的理论位移量，其修正精度高于基于代数距离最小化的Heydemann修正算法(NPL)。本文算法的修正位移与电容式传感器理论位移的平均残差如表2所示。电压为1、2、5 V时，使用本文提出的基于几何距离最小化的Heydemann算法修正后的位移值与电容式传感器理论位移曲线的平均位移残差分别为0.067、0.324、4.360 nm，同时，将修正后位移与Jamin干涉仪解算结果进行对比，可以发现，相同条件下，Jamin干涉仪解算结果的残差较大，电压为1、2、5 V时的平均位移残差分别约为0.591、0.410、7.340 nm。以上对比结果可以说明，经本文算法修正后的位移值较Jamin干涉仪解算算法具有更高的修正精度，其修正结果准确可靠。

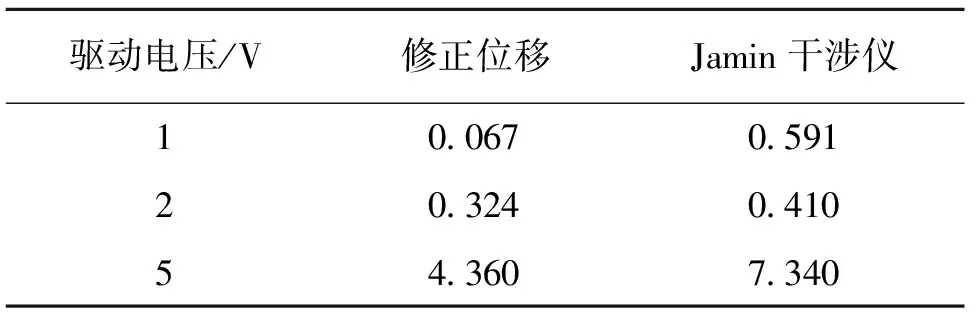
表2 与电容式传感器理论位移的平均残差

5 结 论

本文针对单频激光干涉仪在位移测量中所存在的非线性误差问题，研究了一种基于几何距离最小化的Heydemann修正数学理论模型；利用Jamin干涉仪采集了不同位移行程下的正余弦信号数据，并使用Matlab对修正算法的数学理论模型进行了实验仿真；通过解相，得到了修正后的相位值与位移值，并将修正后的位移与NPL所使用的Jamin干涉仪解算结果进行了详尽的数据对比，完成了修正算法的验证实验。实验结果表明，在不同电压驱动情况下，采用几何距离最小化的修正算法计算得到的位移与纳米位移台电容式传感器理论位移量的平均残差均优于Jamin干涉仪修正结果，且修正位移拟合曲线的拟合优度高，标准差较小，决定系数约等于1，验证了算法模型的修正精度。