页岩断裂韧性实验分析及预测模型建立*

2019-10-24高祥森张明明范翔宇张千贵赵鹏斐

中国海上油气 2019年5期

高祥森张明明朱琳范翔宇张千贵赵鹏斐

(1.中国石油大学胜利学院山东东营 257061；2.西南石油大学四川成都 610500；3.中国石油川庆钻探工程公司川西钻探公司四川成都 610017)

近年来，北美页岩气的商业化开采给世界各国的能源结构调整带来巨大影响，作为常规能源的重要补充，页岩气是缓解原油产量不足，降低化石燃料的有效途径，将成为绿色能源开发的新领域[1-2]。由于页岩的超低渗透率，需要进行水利压裂才能形成工业产能。页岩断裂韧性是研究裂缝起裂、扩展及复杂缝网控制的关键参数。在石油生产中，地层深部岩石只能通过钻井取心获得，很难得到连续的储层岩石断裂韧性剖面，且直接测试试样加工困难，费用高昂[3]。因此，利用页岩断裂韧性与其他物理参数之间的统计关系，并由此预测深部地层岩石的断裂韧性是当前石油工程岩石力学努力解决的问题之一。

李江腾等[4](2006年)认为处于压缩应力状态的裂纹，其裂纹尖端仍处于拉剪应力状态，并通过实验发现I型断裂韧性与抗压强度成正比例关系；Gunsallus(1984年)、Whittaker(1992年)、Bhagat(1985年)等[5-7]均发现岩石I型断裂韧性与抗拉强度存在正比例关系；然而，以上学者仅基于数据统计方法对岩石I型断裂韧性与抗拉强度的相关性提出了一些数据拟合公式，很少从理论上去分析二者的关系。邓华锋等[8](2012年)从理论角度证明了岩石断裂韧性与抗拉强度的相关性，说明了岩石强度与韧性较好的相关性是因为它们引起破坏的力学机制是相同的。Lakshmikantha(2008年)、Zhang(2002年)等[9-10]发现多种岩性岩石I型断裂韧性与抗拉强度也存在幂函数关系。排除以上学者研究中采用试件不同因素，岩石I型断裂韧性与抗拉强度的关系仍需要进一步研究。除抗拉强度外，Chang等[11](2002年)采用一次函数拟合了岩石I型断裂韧性与其声波时差、单轴抗压强度、杨氏模量、泊松比、密度及孔隙度的关系，结果表明断裂韧性与声波时差相关性最好，声波时差随矿物组分、密度，特别是裂缝和缺陷的变化而变化，因此相比于其他物理参数，声波时差能更好地预测页岩抵抗裂纹扩展能力的大小。

鉴于岩石断裂韧性直接测试的复杂性及石油钻井取心的高成本，有必要研究预测深部地层岩石断裂韧性的间接方法。本文采用ISRM建议的标准人字形切槽巴西圆盘(CCNBD)试件测试了取自龙马溪组露头页岩岩样的断裂韧性，同时测定了岩样的部分物理力学参数，如密度、声波时差、抗拉强度、硬度以及页岩矿物组分等，并建立了断裂韧性与这些参数之间的统计关系。由于这些参数可以直接从测井曲线中提取，并建立地层岩石断裂韧性的连续剖面，因而可以方便地用于现场预测岩石的断裂韧性。

1 实验方案设计

岩石断裂韧性比一般的力学参数测试更为复杂和困难，测试方法多样，笔者采用1995年ISRM推荐的CCNBD试件制备龙马溪组露头页岩试样。试件厚度B=30 mm，直径2R=75 mm，初始切槽长度a0=9.89 mm，最终切槽长度a1=24.37 mm。试样几何尺寸如图1所示。

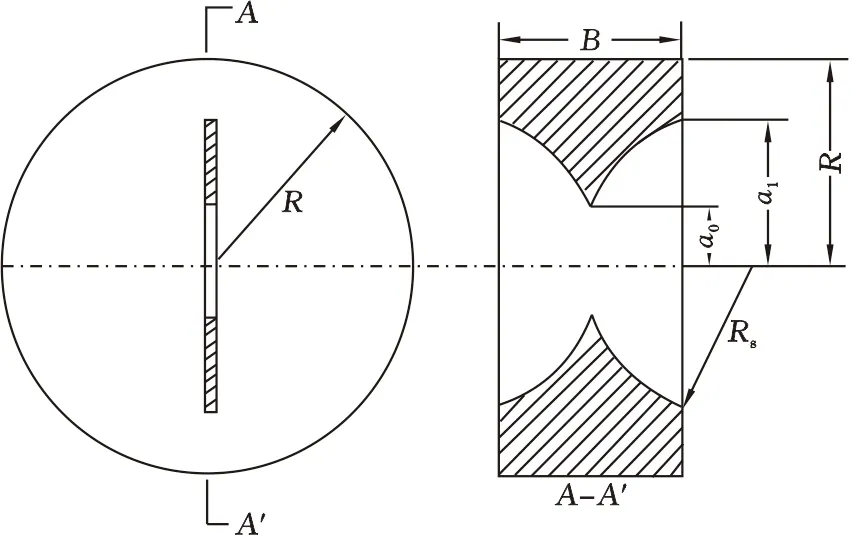
图1 CCNBD试样几何尺寸关系Fig.1 CCNBD geometry relationships

人字形切槽用直径2Rs=52 mm，厚度为1 mm的刀具2次切削而成。试样制备时按照规范严格控制精度，同时在试样切口之前，采用FA2204B型电子天平测量页岩巴西圆盘试样质量，测量精度为10-4g，随后利用自主研发的承压型超声波换能器采用透射法测试页岩试样的纵横波声波时差，声波频率为260 kHz，共测试页岩样品数量15块。

页岩I型断裂韧性试验机为50 kN自动伺服控制材料试验机，其刚度满足岩石断裂韧性测试要求，采用位移加载控制方式，加载速率为100 μm/s，较低的加载速率有利于裂纹沿预测裂纹面的稳定扩展和裂纹尖端断裂过程区的充分发展，能够测得更有效的I型断裂韧性值。试验后，对断裂的半圆盘试样再进行加工处理，制备成尺寸为φ25 mm×30 mm试样，进行硬度试验和圆盘劈裂抗拉试验，页岩I型断裂韧性测试和巴西圆盘试件加工装置分别如图2、3所示。

图2 页岩I型断裂韧性测试Fig.2 Shale I fracture toughness test

图3 CCNBD试样制备Fig.3 Preparation of the CCNBD

2 实验结果分析

2.1 断裂韧性分析

(1)

(2)

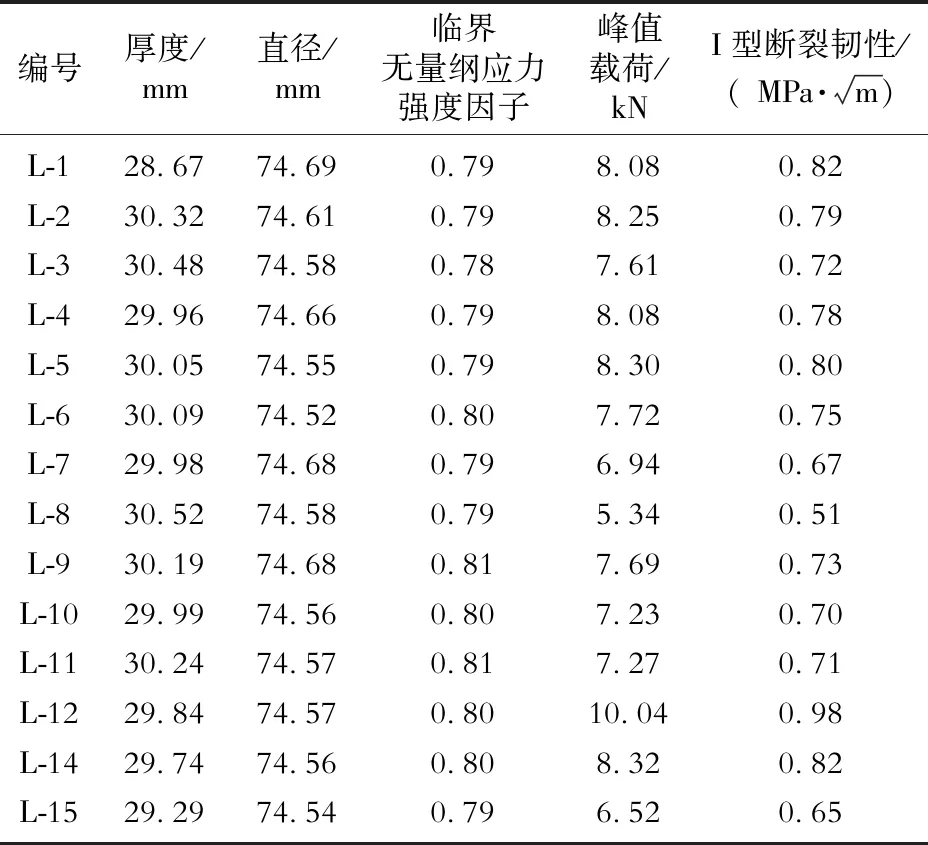
表1 CCNBD试样断裂韧性测试结果Table 1 Tested results of mode I fracture toughness by the CCNBD specimens

对中心直裂纹CSTBD试件的应力强度因子使用相同的因子无量纲化，与CCNBD试件进行对比。应力强度因子手册中给出的CSTBD无量纲应力强度因子解[18]为：

3.181 8α3+10.009 62α4-20.778 2α5+

20.134 2α6-7.506 7α7)

(3)

(4)

式(4)中：Y*为CCNBD试件无量纲应力强度因子；α0为相对初始切槽长度,α0=a0/R。

图4 CCNBD标准试样临界无量纲应力强度因子Fig.4 The critical dimensional stress intensity factor and its limit on standard sample of CCNBD

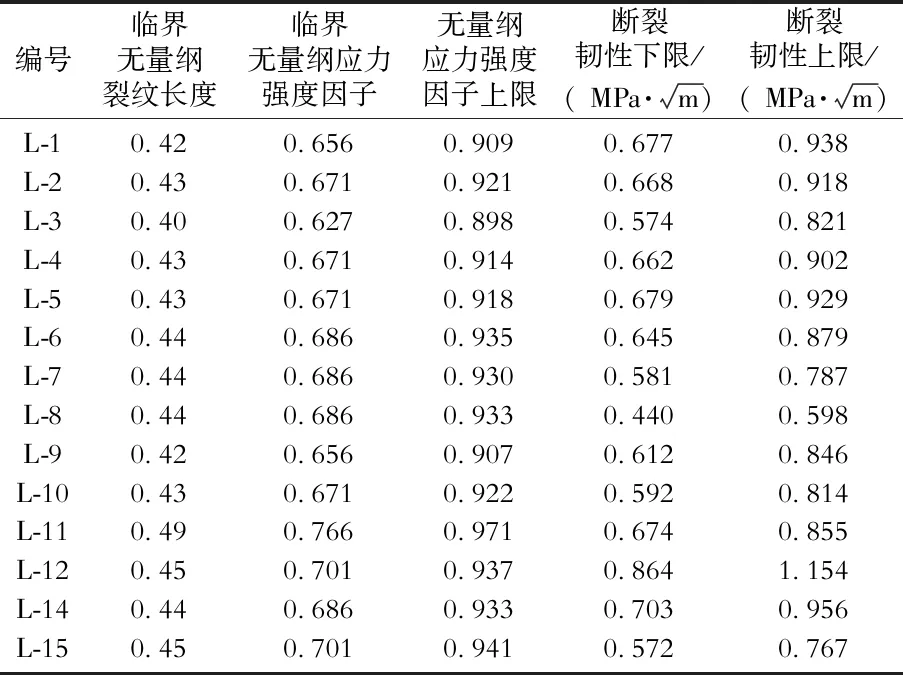
表2 页岩试样临界无量纲裂纹长度及断裂韧性上下限Table 2 The critical dimensional length of crack and fracture toughness limit for shale samples

2.2 其他物理力学参数测试结果

对取自龙马溪组露头页岩加工好的圆盘试样进行抗拉强度和硬度实验，测试条件与断裂韧性保持一致。抗拉强度及硬度的计算公式见式(5)、(6)，试样密度、声波时差及抗拉强度和硬度测试结果见表3。

(5)

(6)

式(5)、(6)中：σt为页岩抗拉强度，MPa；D为圆盘试样直径，mm;L为圆盘试样长度,mm；F为页岩硬度，MPa；S为压头表面积,mm2。

表3 页岩试样其他物理力学参数测试结果Table 3 Other physico-mechanical properties of the shale samples

3 断裂韧性预测模型建立

根据表3实验结果，利用最小二乘法回归得到页岩I型断裂韧性与密度、声波时差、抗拉强度及硬度的关系，并对页岩I型断裂韧性与其他物理参数的相关性进行了研究，如图5所示。

由图5a可以看出，在页岩断裂韧性与密度空间内，数据点分布离散，但随密度的增大，断裂韧性平均值出现增大的趋势。由图5b、c可以看出，随纵横波声波时差增大，断裂韧性逐渐减小，线性回归函数能够较好地表示两者的相关性。图5d可以看出，断裂韧性与抗拉强度成正比，且具有很好的相关性，去掉2个奇异点后再次拟合，两者间的相关系数达到0.972 1。由图5e可以看出，随着硬度的增大，断裂韧性逐渐增大。

对比分析发现，页岩I型断裂韧性与密度的相关性最差，试验选取的页岩样品密度变化很小(2.45～2.49 g/cm3)，在如此小的变化范围之内，不适于用来预测其他参数，KIc与ρ的相关系数仅为0.081 2；页岩I型断裂韧性与硬度相关性较差，两者间相关系数为0.344 7；页岩I型断裂韧性与声波时差成反比例关系，相关性稍差于抗拉强度，与纵波时差的相关系数为0.614 4，与横波时差的相关系数为0.701 9。

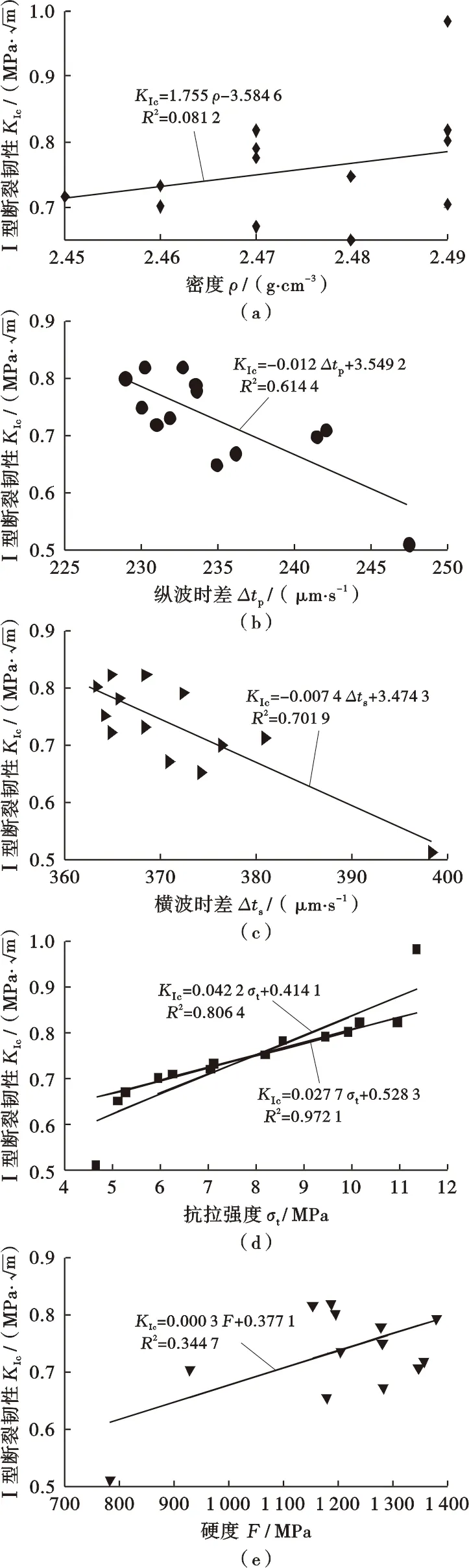
图5 页岩I型断裂韧性与密度、纵波时差、横波时差、抗拉强度、硬度之间关系Fig.5 Relationship among fracture toughness and density，compressional slowness，shear slowness，tensile strength and hardness

根据图5数据曲线的分析，可以看出页岩断裂韧性与其他物理力学参数的线性关系较好，且线性关系更加符合岩石不同力学参数间的物理性质。因此，笔者根据测得的多个物理力学参数(表3)对断裂韧性进行了线性多元逐步回归分析，并得到如下预测模型：

KIc=1.433 27+0.028 89σt-0.008 6Δts-0.009 685Δtp

(R2=0.958 7)

(7)

式(7)中：Δts为横波时差，μm/s；Δtp为纵波时差，μm/s。

利用本文建立的多元线性预测模型预测的页岩I型断裂韧性值与实测值对比如图6所示。由图6可以看出，页岩I型断裂韧性预测值与实测值较为吻合，精确度高。由于页岩断裂韧性直接测试的复杂性，可以利用本文建立的多元线性预测模型对页岩I型断裂韧性进行预测。岩石的声波时差、密度、强度等信息都可以从测井曲线中获得，因此利用本文建立的预测模型可用于现场计算岩石断裂韧性值，得到储层岩石断裂韧性连续剖面。