基于MODAPTS的汽车座椅装配线平衡优化研究

石展晴 胡佳宁 熊燕华

(南京农业大学 工学院，江苏 南京 210031)

0 引言

现代汽车座椅装配一般采用装配流水线方式，将装配过程划分为若干作业单元并合理安排到各工位上。由于各工位同时作业，装配线平衡率对企业效益尤为重要。

装配线平衡问题自从1955年Salveson 首次提出以来 ,学者们展开了大量研究。Barathwaj等[1]以工站间和工站内部工作负荷指数最小为目标，提出了一种基于装配线平衡问题的遗传算法(GA)；Hossein[2]等提出了装配工人姿态平衡问题模型，通过工人姿态平衡改进装配线配置；Zhang[3]提出了一种改进的遗传算法来解决装配线两侧平衡问题；韩煜东等[4]在考虑产品需求速率的前提下，提出了调整加工成本的新方法，建立了混流装配线平衡问题的多目标优化模型；公绪霞等[5]采用模糊优化理论，建立了装配线平衡问题的多目标非线性规划模型；徐立云等[6]构建了最少工位数和最小工位累计疲劳度标准差的多目标优化模型，基于优先权重进行编码，设计多目标粒子群算法求解；焦玉玲等[7]综合考虑作业元素的时间及位置阶位值，运用改进阶位法对装配线平衡问题求解；李爱平等[8]提出一种考虑装配关系复杂性的改进型多目标装配线平衡优化方法，并对遗传算法的交叉环节利用模糊聚类算法作出改进。

已有研究主要是以装配线平衡率相关指标为目标建立数学模型求解，从而重排最小作业单元，以改善效果，但只是理论推导，并未模拟验证。实际生产过程中，工人的标准动作及时间也会影响平衡率，且重排作业单元将耗费企业大量资源。本文分析装配线平衡率不高的原因，针对耗时动作和瓶颈工序进行优化，利用MODPATS预定标准工时，并导入Plant Simulation中仿真验证改善效果。该方法对结果进行仿真验证，使改善效果更具可信度，规范了动作，减少了工人疲劳度，对企业优化装配线平衡率有一定借鉴作用。

1 MODPATS标准工时系统的制定

1.1 MODPATS标准装配动作定义与分类

对座椅装配过程中基本动作进行分类，将标准动作划分为取用动作、无工具动作、工具操作、辅助动作以及其它动作。根据MODPATS法基本定义，将各动作用模特法代码计算出模特值，取1MOD=0.129s，计算各类动作的时间，如表1所示。

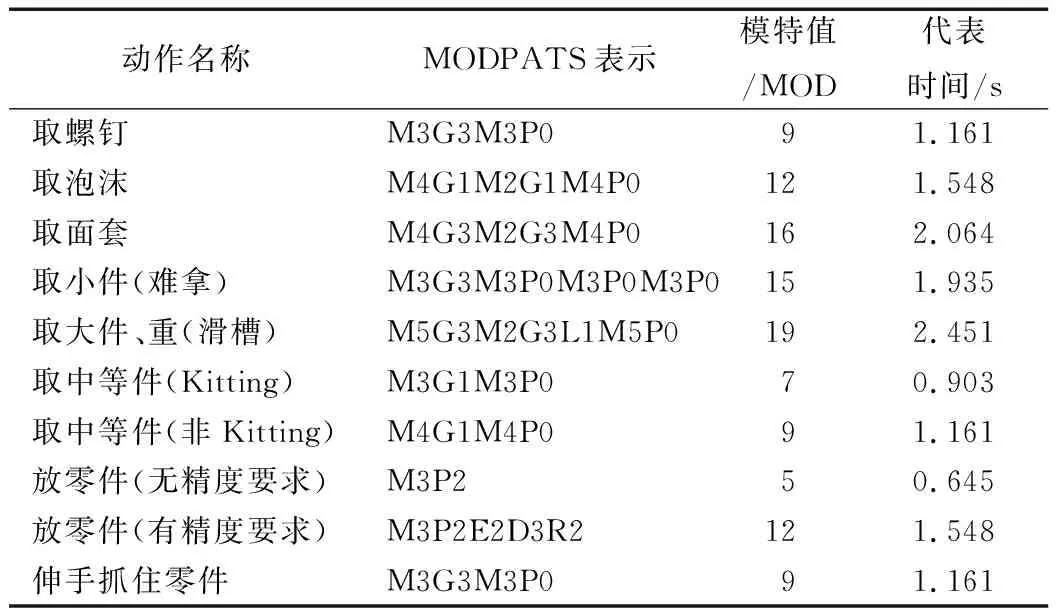
表1 标准动作分类代码及时间表示例

1.2 座椅装配标准工时计算

MODPATS法得出的时间与实际测时较为接近，具有线性关系，由于测时受偶然因素影响，要得到精确结果，需要测试的数据量较大，因此采用MOD值经过宽放得出标准工时。根据该公司实际，总宽放率=疲劳宽放(5%)+私事宽放(3%)+操作宽放(2%)=10%。

JIT PROCESS BOOK表格[9]可记录各工步并分解为标准动作，根据MODPATS法，利用标准动作预定标准时间，经宽放得出标准工时。统计得出各工位的标准时间如表2所示。

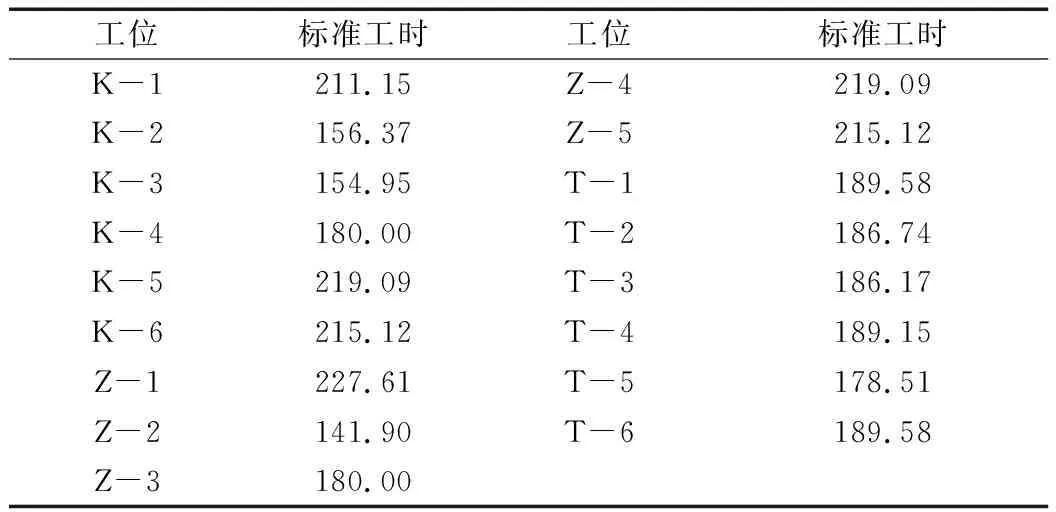
表2 标准工时统计

2 座椅装配线平衡优化设计

2.1 装配线平衡问题分析

2.1.1 装配线平衡的评价指标

(1)生产节拍：

CT=max(Ti)=227.61s

(2)工作站负荷率：

工作站负荷率反映该工作站利用效率，值越大说明利用率越高，结果如表3所示。

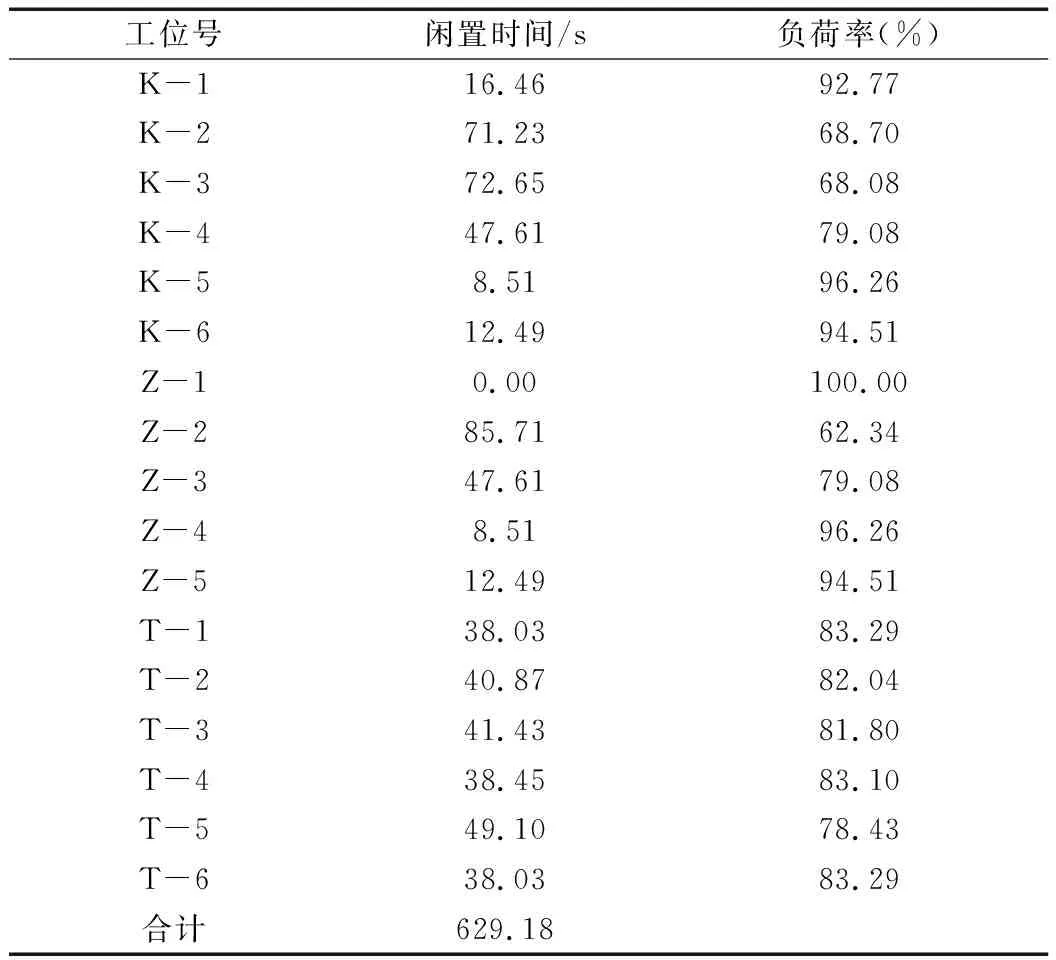
表3 闲置时间及负荷率统计

(3)装配线闲置率：

其中，TXi为各工序闲置工时，CT为生产节拍，n为作业工位数。

(4)装配线平衡率：

(1)

(5)生产平衡损失率：

d=1-LBR=16.26%

平衡损失评价表[10]如表4所示。

表4 平衡损失评价结果

(5)平滑性指数：

(2)

该指标反映各工站时间分布离散度，SI值越大，则各工位作业时间分布越分散。

2.1.2 装配线平衡性能分析

对照平衡损失评价表，该公司生产平衡损失率高于10%，平衡率为良；有3个工位负荷率低于70%，闲置率高达16.26%，意味着在装配过程中，16.26%的时间由于生产装配线配置不平衡而损失了；Z-2工位在227s的节拍中浪费了86s的时间。综上，装配线不平衡对生产率及公司效益影响较大。

表3显示，生产线平衡率较低的工位有K-1、K-5、K-6、Z-1、Z-4、Z-5。如果这6个工位时间能降低，就可以提高生产线效率。合装工位闲置时间普遍较长，可以通过最小作业单位重排将其重新分配，以使得装配线平衡率提高。

2.2 程序分析法下的动作优化

将装配过程中各动作的使用次数统计后排序如表5所示，其中，注“*”的为增值动作。

表5显示，使用次数前20的动作中17个属于非增值动作，应尽量减少这些动作或减少该动作的操作时间。采用5WHY和5W1H方法改善这些动作。

(1)针对非瓶颈工序。如取中等件(非Kitting)，采用5WHY提问法，找出问题根本原因所在，然后针对根本原因，根据ECRS原则取消多次动作合并为一次，根据动作经济原则，将物料摆放位置更加合理化，减少动作浪费及工人负担。

表5 频繁使用动作统计结果

(2)针对瓶颈工序Z-1。分析Z-1最小作业单元与时间，如表6所示。

表6 Z-1主要工步与时间

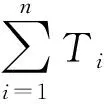
2.3 动作优化的改善效果

2.3.1 改善后标准时间统计

将改善后各动作及标准工时绘制成JIT PROCESS BOOK标准表格，统计标准时间结果如表7所示。

2.3.2 改善后的平衡性能分析

(1)生产节拍：

CT=max(Ti)=190.71s

(2)装配线闲置率：

(3)装配线平衡率：

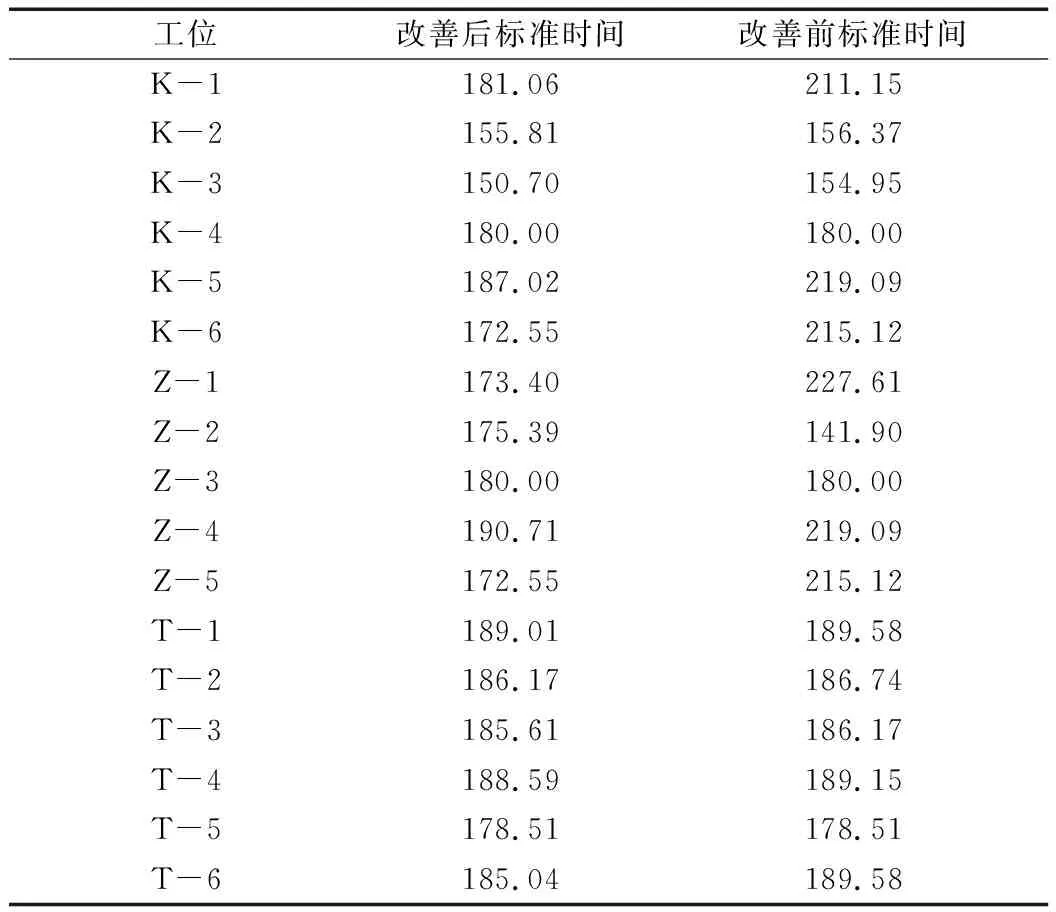
表7 改善前后时间对比

(4)生产平衡损失率：

d=1-LBR=15.52%

(5)平滑性指数：

改善后平衡损失率在10%以下，平衡率为优。

2.3.3 改善前后平衡性能对比

绘制改善前后时间对比如图1所示。

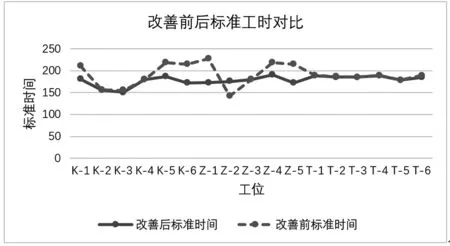
图1 改善前后标准工时对比

经过改善，折线图更加平缓，陡峭的弯折点也已消失，瓶颈工序改变由Z-1变为Z-4，分析改善后平衡性能如表8所示。

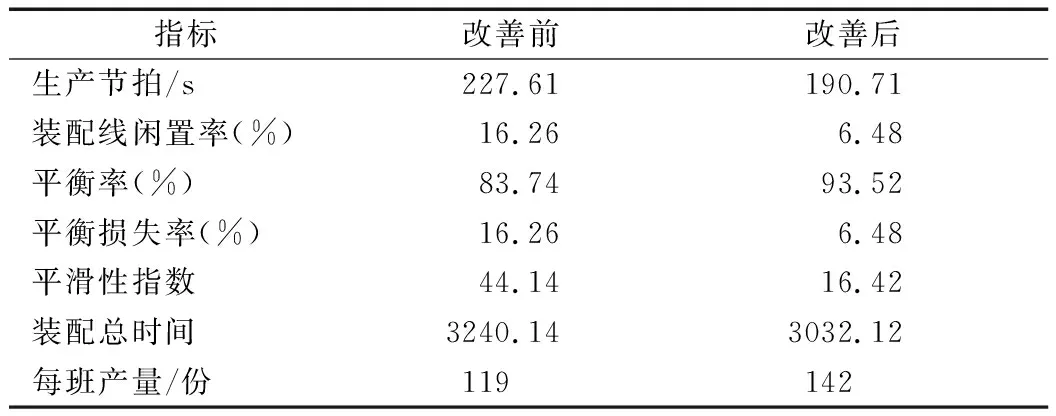
表8 改善前后各平衡指标对比

(1)改善后的生产节拍减少36.89s，班产由119份增加到142份，生产效率提高19.35%，不增加工人的情况下公司多盈利。

(2)生产线平衡率上升近10%，装配线闲置率下降近10%，平滑性指数下降，说明各工位装配时间接近，装配线平衡性能明显提高，缓冲区货物不会发生严重堆积，减少暂存区的浪费[11]。

(3)减轻了工人的劳动强度，通过改善作业顺序、动作顺序、工具摆放问题，使得工人取消了不必要的多余动作，每生产一份座椅减少735个模特值。

3 动作优化改善效果的仿真验证

3.1 仿真模型建立

采用Plant Simulation仿真软件，将实际系统中的复杂问题简化为Flow Shop(流水作业生产线)模型[12]，并进行以下定义及简化：①模型中各元素的顺序为装配过程的逻辑顺序；②在装配过程中，由于工位之间搬运距离较短，因此将其抽象为缓存区，模型中机器操作简化为时间延迟；③假设在仿真运行期间，没有发生故障；④以MODAPTS测算的标准工时为基础，在σ=2s范围内上下波动。

装配线平衡问题ALBP (Assembly Line Balancing Problem) 一般按其优化目标分为以下几类[13]:最小化工作站数、最小化生产节拍、最大化装配线生产率、平衡装配线各工位负荷(负荷均衡化)。本文以负荷均衡化为仿真优化目标建立仿真模型，设置T-1工位的组装规则，设置各装配工站加工时间参数，如表7所示，仿真总时间为30天，建立仿真模型效果图如图2所示。

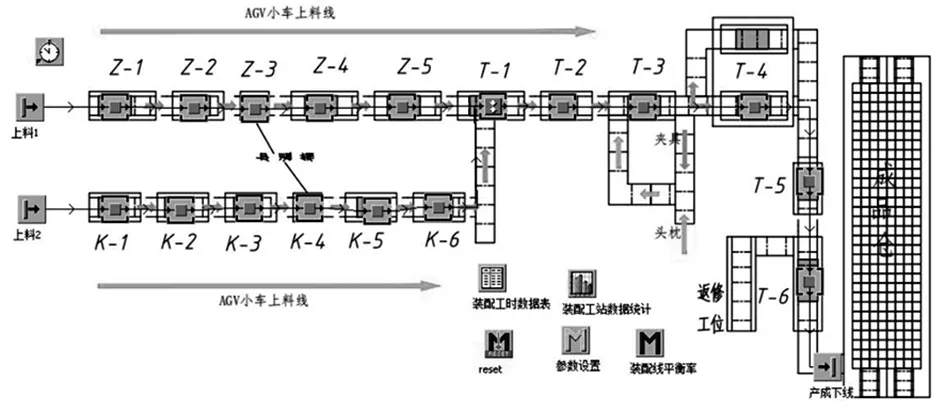
图2 座椅装配仿真模型效果

3.2 仿真结果

运行仿真模型，得到改善前后各装配工站实时负荷柱状图和曲线图，如图3、4所示。从仿真实验的最终数据可以看出，改善前后工位平均负荷率与模特法测时计算出的装配线负荷率大体接近，验证了动作优化改善效果的合理性。

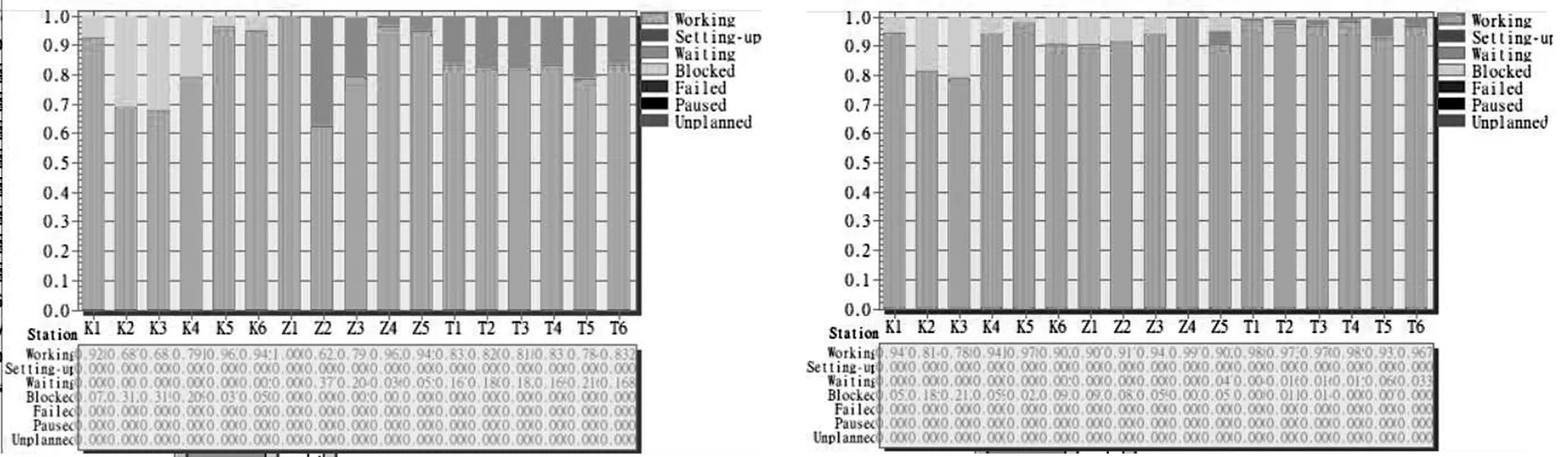
图3 改善前(左)后(右)装配工位实时负荷柱状

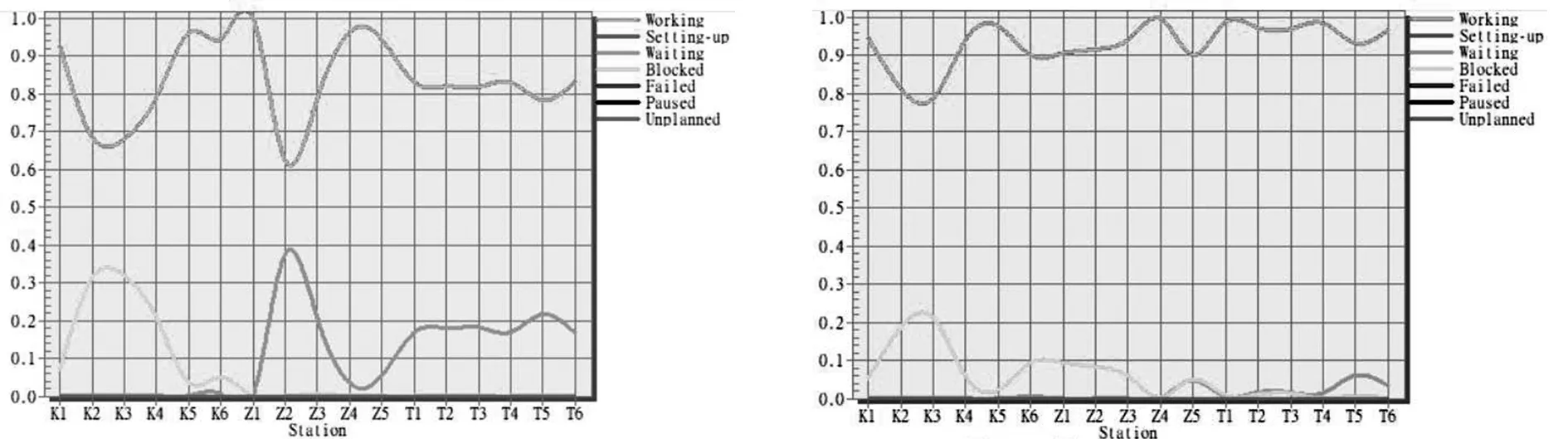
图4 改善前(左)后(右)装配工位实时负荷曲线

4 结语

针对汽车前排座椅装配线平衡问题，采用模特法与仿真分析法相结合的方式进行研究。首先，通过建立基于MODAPTS的工时测算系统，分析装配工序的标准作业时间，以装配线平衡率、工位负荷率和平滑性指数等多重因子为评价指标，改善装配线平衡率。其次，对装配流水线上耗时且频繁的动作，运用动作分析改善原理及步骤进行改善，对瓶颈工序采用最小作业重排法进行分解重排。最后，利用Plant Simulation仿真分析方法验证改善前后的效果，使结果更加可靠。案例研究结果表明，应用MODAPTS法预定标准工时并优化动作，有利于提高装配线平衡率，并减少工人的疲劳度。