基于深度学习的波浪能发电功率预测
2020-06-11张明宇蔡夫鸿王鑫红
张明宇,赵 猛*,蔡夫鸿,梁 钰,王鑫红
(1.海南大学 机电工程学院,海南 海口 570228;2.海南电网有限责任公司 电力科学研究院,海南 海口 570105;3.东北电力大学 建筑工程学院,吉林 吉林 132012)
波浪能作为未来极具潜力的新能源品类,研究其发电稳定技术及并网调度技术对于沿海城市、半岛城市、海岛城市能源供给具有实际意义。对于西沙群岛等远洋海岛,由于无法从大陆直接获取电能,大规模开发波浪能有重要战略意义[1-4]。
针对波浪能发电船等发电装置输出功率波动性较大的问题,准确的功率预测是一种有效的解决途径。波浪能发电预测按时间尺度可分为超短期预测(≤4 h)、短期预测(≤72 h)、中长期预测(30~365 d),通常时间尺度划分并无严格的规定,只需根据预测功能不同进行粗略设定[5-8]。超短期预测用于提供功率瞬变信息;短期预测用于调度计划制定、负荷跟踪和预测电力市场等;中长期预测用于资源评估和电站规划等。按空间尺度可分为单场预测、区域预测。单场预测用于指导波浪能电站运营,区域预测用于辅助调度部门进行波浪发电功率波动预估,并制定多种电源协调调度计划[9-13]。
目前关于波浪能预测的研究不多,文献[14]建立风-浪经验模型,并通过灰色模型对波浪要素预测结果进行残差修正,然后利用阿基米德波浪摆(AWS)系统建立波浪要素和波浪能发电功率之间转换模型。类似的转换模型还有WAM(wave model)、WAVEWATCH、STWAVE(steady-state spectral wave)和 SWAN(simulation waves nearshore)等。此类模型的明显缺点在于运算时间较长,从而不适用于对电力系统的实时调度。文献[15]提出先将涌浪和风浪分离,然后再利用ARIMA时间序列预测方法进行波浪能短期预测。该方法简单考虑风与浪的能量传递模式,而忽略了温度、光照等可参照的环境因素。波浪能的能量不仅仅需要考虑风能,其也间接来自于太阳能,所以光照强度、温度等也是重要的考量因素。
针对这一问题,本文LSTM-BP模型第一部分使用长短期记忆网络(LSTM)算法预测风速、温度、光照强度等气候数据。LSTM是一种有“记忆”的时间序列预测模型,时间序列预测的主要方法包括传统的时间序列预测方法和基于机器学习的方法[16-18]。其中,传统时间序列预测方法主要是在时间序列参数模型的基础上求解出模型参数,并利用求解出的模型完成预测工作。经典时间序列模型包括移动平均模型(moving average,MA)和自动回归平移模型(auto regressive moving average,ARMA)等。基于机器学习的方法包括贝叶斯网络(Bayes net,BN)和支持向量机(support vector machine,SVM)等。随着神经网络和深度学习方法的崛起,特别是LSTM在时间序列预测方面的优良特性,促使越来越多的研究者将视线转移至基于深度学习的时间序列预测方法上[19-20]。
本文模型的第二部分利用BP网络和第一部分得到的气候数据预测波浪能发电功率。不同于文献[14]中提到的AWS模型,BP网络通过采用深层非线性网络结构拟合实际对象复杂内在关系,可避免繁琐物理建模过程,有较好的泛化能力和容错能力。本文设计以预测时间尺度为因变量的对比实验,实验结果表明,对比不同时间尺度的预测结果,利用长时间跨度的历史气候数据和功率数据,本文的LSTM-BP模型可以得到准确的预测结果。
1 LSTM-BP预测模型
神经网络由大量的非线性神经元构成,从输入到输出需经过非常复杂的非线性运算。同时通过反向传播算法调整神经元之间的连接权重,最终实现网络输出与样本输出差值(Loss)向零逼近。神经网络特别适用于输入与输出取值容易量测,而两者间的关系不易通过物理机理分析获取的情形。例如气候数据的预测问题,本质是以当前数据作为输入,未来某时刻的取值作为输出的建模过程。传统的建模过程较为复杂,而利用LSTM模型的拟合过程则比较简单,模型训练好以后,正向计算速度也比传统的模型速度更快[21]。
1.1 LSTM模型
LSTM继承了RNN(recurrent neural network)的优良特性并解决了标准RNN中的梯度消失和梯度爆炸问题。LSTM是目前应用最为广泛和成功的RNN模型。LSTM单元结构如图1所示[22]。

图1 LSTM网络结构Fig. 1 LSTM network structure
由图1可知,LSTM的结构包括输入门、输出门、遗忘门以及各个部分的前向运算关系。此外,从图中容易看出,在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态ht外,还多了另一个隐藏状态,这个隐藏状态即是所谓的细胞状态(cell state),记为Ct。
顾名思义,遗忘门(forget gate)用于决定控制是否被遗忘,其在LSTM中以一定的概率控制着是否遗忘上一层的隐藏细胞状态。遗忘门的输入包括上一序列的隐藏状态ht和本序列数据xt,两者通过一个激活函数(一般采用sigmoid)获得输出ft。由于sigmoid的输出在[0,1]之间,因此这里的输出代表了遗忘上一层的概率。完整的表达式为
ft=σ(Wf[ht-1,xt]+bf)。
(1)
式中:Wf、bf为线性关系的系数和偏置;[ht-1,xt]是通过对ht-1、xt拼接而成;σ为sigmoid激活函数。
输入门(input gate)负责处理当前序列位置的输入。从图1中可以看出,输入门由2部分组成,其中第一部分使用了sigmoid激活函数,输出为it,而第二部分使用了tanh激活函数,输出为zt,两者的结果相乘用于更新细胞状态。完整的公式如下:
it=σ(Wi[ht-1,xt]+bi),
(2)
zt=σ(Wz[ht-1,xt]+bz)。
(3)
在研究输出门之前,需留意LSTM的遗忘门和输入门的结果会作用于细胞状态Ct,图1中可以看出细胞状态Ct-1到Ct的运算过程。Ct由2部分组成:第一部分是Ct-1和遗忘门输出ft的乘积,第二部分是输入门的it和zt的乘积。
得到更新的隐藏细胞状态Ct后,则可用来计算输出门(output gate)。输出门的计算包括输出状态ot和隐藏状态ht的计算。从图1中可以看出,ot依然是在[ht-1,xt]上加上权重和偏置后用作sigmoid函数的输入,然后由ot和Ct计算得到新的隐藏状态ht,其公式如下:
ot=σ(Wo[ht-1,xt]+bo),
(4)
ht=ot⊙tanh(Ct)。
(5)
1.2 BP模型

图2 BP神经网络Fig. 2 BP neural network
BP网络在1986年就被Rumehard等人提出,由于当时计算机的计算力不高,所以并未得到发展。在BP基础上衍生出很多神经网络模型,如卷积网络和LSTM。BP网络一般包含输入层(i层)、隐含层(h层)、输出层(o层)。图2所示是各层神经元数量为[3,3,2]的一个网络,从左到右边分别是i层、h层和o层。h层和o层神经元Cell中的前向计算公式为
y=σ(W⊙X+b)。
(6)
式中:W表示神经元之间链接的权重矩阵,矩阵的行列分别是前一层神经元和后一层神经元的个数;X表示链接左侧神经元的输出;b表示神经元中的偏置矩阵;y表示一层神经元的输出矩阵[23]。
2 数据及处理方法

图3 数据处理流程Fig. 3 Data processing flow chart
结合获取到的气候数据和功率数据特点,本章提出一系列数据预处理过程,数据处理流程及算法过程如图3所示。
2.1 数据选取
目前,可用于波浪能预测的数据主要来源于国家海洋信息监测中心单个监测台采集的数据和波浪能发电站中记录的数据。主要涉及温度、光照强度、风速、波浪高度、发电功率等基本信息。本文实验数据来自我国某波浪能发电船上采集到的功率数据及当地气象台获取的气象数据。
基于LSTM-BP的波浪能发电功率预测过程由2部分组成。第一部分运用LSTM完成对气候数据的预测,其将历史序列作为输入,即图1中的xt,输出是未来某一时刻的值xt+1。此部分需要建立的数据集是某海岛2017—2018年的日照强度、温度、风速三维度气候数据,采集时间间隔1 min,总共大约有300万条数据。预测得到的三维度序列数据分别用S(日照强度)、T(温度)、W(风速)表示。第二部分运用BP网络,实现发电功率的拟合。该部分通过获取某发电厂245 d中每天的发电量,构成BP模型的输出标签数据库。BP模型的输入为第一部分预测得到的S、T、W数据。但此类数据不能直接用来构成输入神经元,因为S、T、W一天的数据量为4 320个,而程序中如果使用4 320个输入神经元,数量庞大的输入层将无法进行模型的训练,也不利于体现输入数据的特征。因此,本文提取S、T、W数据的特征作为输入神经元,具体包括微分值均值(d)、最大值(max)、最小值(min)和均值(average)4个维度总共12个特征,其中微分均值体现数据变化的剧烈程度,其他特征容易理解。输出层为当天的平均功率P,可用简化公式表示为
P=f(Sd,Smax,Smin,Saverage,Td,Tmax,Tmin,Taverage,Wd,Wmax,Wmin,Waverage)。
(7)
2.2 数据预处理
在做归一化之前,需要观察原始数据是否存在异常值或缺失值。常用的异常处理方法为设定阈值法,在其判定为异常值后使用双侧高斯权重插值法(本文不考虑连续出现异常的情况),而对于具有数据缺失的情况则采用单侧高斯权重插值法,插值计算公式为
(8)

图4 处理前温度数据Fig. 4 Temperature data before processing

图5 处理后温度数据Fig. 5 Temperature data after processing
对比图4、5可以看出,数值异常大的数据被剔除掉,处理后的数据较好地体现了数据的特征。对于传统的建模与仿真来说,不同对象有不同类型的数据和不同量纲的数据,一般需要保留原始数据的量纲或者只进行简单的简化。而在神经网络训练时,需要剔除原始数据的具体含义和量纲,仅仅保留数据间的关系特征,并对输入数据和输出数据进行归一化处理,归一化数据的取值范围为[0,1]。本文使用简单的离差标准化方法(min-max normalization)进行归一化,公式为
(9)
式中:X为原始训练数据,Xmax为原始数据中最大的值,Xmin为最小值,X*为归一化值。
2.3 训练数据构造
结合前文提及的模型和数据特点,进行训练数据的构造。本文采用定长输入LSTM,根据参数的不同构造不同的预测时间尺度,输入时间尺度分别为5、60、1 440 min。获取预处理后数据中时间靠前的80%数据量用作训练模型,剩余的20%用作模型测试。其中用作测试的数据时间尺度必须涵盖给出的发电量数据的时间尺度。同理,在做功率预测时也需要将LSTM预测的数据和功率数据分为训练集和测试集。
3 LSTM-BP模型验证实验
3.1 实验环境
本文实验的硬件平台:Intel(R)CoreTMi5-6300H, 2.3 GHz CPU,内存16 GiB;软件实验平台:Ubuntu16操作系统、python3.5编译器和Tensorflow1.12深度学习框架。
3.2 基于LSTM的气候数据预测
本实验目的在于观察LSTM模型在3个时间跨度(5、60、1 440 min)下预测效果的差异并分析其原因,将最后的功率预测均方差作为实验的参照标准。通过LSTM模型预测气候数据,并计算上文提到的4个维度的特征值作为BP的输入,利用BP模型进行功率拟合,BP每一层神经元数量选择为[121,510,1]。训练完成后,测试集和训练集分别通过公式(10)计算预测值的均方误差。
(10)


表1 气候预测方差
观察表1和图6发现:①测试集的均方差都比对应训练集的均方差大,这是由预测模型的泛化特性决定的;②只考虑气候因素为因变量而其他条件保持一致,发现日照的均方差普遍小于温度均方差,风速均方差最大,说明气候数据中日照数据规律性最强,预测最准;③预测时间跨度越长,对应均方差越大,所以预测效果越差,而且风速预测结果在各个时间尺度上方差都是最大的,说明风速数据的规律性最差;④图6(c)的风速数据基本不能获得预测数据max、min、d的特征,只能给出一条比较平滑的曲线,而图6(a)和图6(b)能够比较好地体现预测数据的特征。综上可得出结论:在同一气候维度,时间尺度越大数据预测的拟合程度越差,也就是预测效果越差。

图6 气候预测Fig. 6 Climate prediction comparison
3.3 波浪能发电功率预测
采用LSTM模型预测的气候数据作为输入,输出数据为某波浪能发电船245 d的发电数据,该数据的时间跨度是气候数据时间跨度的子集。同理,首先对发电数据进行预处理,然后根据预测得来的气候数据计算4个维度的特征数据,并结合功率数据构成BP模型训练数据库,维度是245行、5列。实验同样分3组进行,输入是预测跨度分别是5、60、1 440 min的气候特征数据,输出是波浪能发电单日出力数据,总共245个功率数据,其中训练集是时间靠前的200个数据,测试集是后45个。利用BP模型进行发电功率预测,预测准确性以均方差衡量,预测结果如表2所示,预测效果如图7所示。

表2 功率预测方差
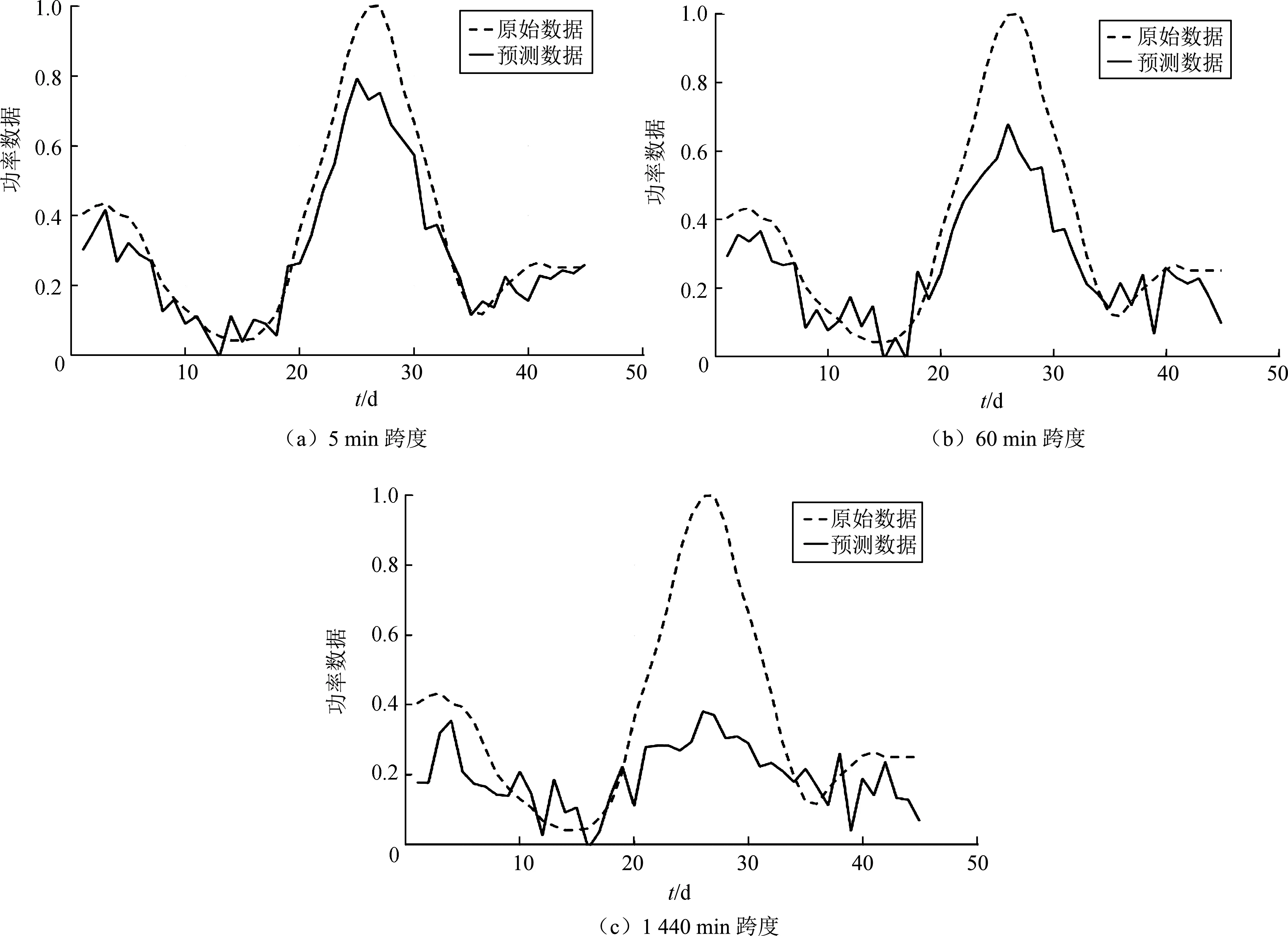
图7 功率预测对比Fig. 7 Power prediction comparison
观察表2和图7发现:①测试集的均方差比训练集的大,这是由预测模型泛化特性决定的;②预测时间跨度作为考虑变量,可以看出时间尺度越大,在训练集和测试集上的均方差越大,这一特点是因为BP模型的输入是气候的特征数据,预测时间尺度越短,数据的特征越容易体现出来;③在实际功率较高的时候(0.6~1.0),预测结果普遍低于实际功率,而且预测时间尺度越大误差越大,而当实际功率在较低的范围(0~0.4),预测结果比较准确,原因是训练样本量太少而且样本中高功率数据和低功率数据比例严重失衡。
4 结论
本文利用某海岛气候数据和波浪能发电船发电数据建立历史数据库。舍弃传统的、复杂的物理建模过程,仅仅运用深度学习预测模型,给出了一种基于历史气候数据的波浪能发电功率预测方法,分析了在不同的时间尺度下预测准确程度差异性及其产生的内在原因。发电船储能系统可以根据气候预测和功率预测结果,做出储能还是释能的决策。本文方法尚未涉及波浪参数对实验结果的影响,后续工作将继续研究波浪参数对功率预测的影响以及探索涌浪分离方法与深度学习模型的结合,也将进一步考虑在模型中加入attention机制后的预测效果。
