非单调变分不等式问题的双投影算法研究

徐紫文

(四川师范大学 数学科学学院，四川 成都 610068)

考虑经典变分不等式问题：求x*∈C，使得对任意x∈C，都有以下不等式成立，

〈F(x*)，x-x*〉≥0。

(1)

式中F：Rn→Rn是连续映射，C是Rn上的一个非空闭凸子集，用SOL(C，F)表示变分不等式VI(C，F)的解集，简记为S，〈·，·〉是欧氏内积。变分不等式问题是优化理论中重要分支，并在工业、经济、管理学、网络运输及交通运输等领域都有极其重要的地位[1-4]。投影算法作为求解变分不等式问题的重要算法之一，吸引了众多学者的关注和研究[5-7]。最经典的变分不等式在20世纪60年代由Hartman-Stampacchia[8]提出。投影算法最初源于Goldstein[9]和Levitin-Polyak[10]，在映射F是强单调和Lipschtz连续的条件下，建立了算法的全局收敛性。 该投影算法的假设条件太强，大大地限制了其适用范围。随后Korpelevich[11]提出了外梯度算法，此算法将映射F是强单调削弱为伪单调，其算法在每次迭代过程中都需计算2次投影。此算法虽然将强单调假设条件削弱到了伪单调，但由于其Lipschtz连续的条件依然很强，仍然存在很大的局限性。1997年Iusem[12]引入Armijo-type线性搜索, 将Lipschtz连续条件削弱为连续，详细发展过程与具体情况见文献[13-14]。该方法仍然对映射F单调性有所要求，使其在实际应用中仍有局限。最近，在文献[16]中，Ye M L和He Y R仅在其对偶变分不等式有解的条件下，提出一类改进的新双投影算法， 该算法不假设任何单调性条件，大大扩大了其适用范围。受其启发，本文通过构造投影算子的一个新的投影区域，提出一种求解非单调变分不等式的改进的双投影算法。 数值实验表明新的算法有效，比文献[16]中的算法收敛更快。

本文的内容安排如下：第1章回顾一些基本定义与基本结论；第2章提出本文算法；第3章给出本文算法的全局收敛性的相关证明；第4章用数值实验来检验算法的有效性。

1 预备知识

先回顾一些概念和结论，以助于后面的证明。本文后面‖·‖均指欧氏范数。

定义1变分不等式问题(1)的对偶变分不等式为：求x*∈C，使得对所有的x∈C都满足

〈F(x)，x-x*〉≥0。

(2)

式中C是Rn的一个非空闭凸集。记问题(2)及其解集分别为DVIP(C，F)和SD。

引理1[15]x*∈SOL(C，F)⟺‖rμ(x*)‖=0，其中μ>0。

引理2[16]若F是连续的且C是非空闭凸集，则SD⊂S。

引理3[17]设C⊂Rn是一个非空闭凸集，x∈Rn，以下不等式成立：

〈x-PC(x)，y-PC(x)〉≤0，∀y∈C。

定义3映射F：C⊆Rn→Rn，任给x，y∈C，ξ>0，L>0，若

① 〈F(y)-F(x)，y-x〉≥ξ‖y-x‖2，则称F在C上是强单调的，ξ是F在C上的强单调系数；

② 〈F(y)-F(x)，y-x〉≥0，则称F在C上是单调的；

③ 〈F(x)，y-x〉≥0⟹〈F(y)，y-x〉≥0，则称F在C上是伪单调的；

④ ‖F(y)-F(x)‖≤L‖y-x‖，则称F在C上是Lipschtz连续的，L是F在C上的Lipschtz常数。

引理4[18]若x∈C，μ>0，则〈F(xk)，rμ(xk)〉≥u-1‖rμ(xk)‖2。

引理5[18]设C⊆Rn是一个非空闭凸集，T是Rn上的实值函数，记H：={x∈C|T(x)≤0}。若H非空并且T在C上θ-Lipschitz连续(θ>0)，则对任意x∈C，以下不等式成立：dist(x，H)≥θ-1max{0，T(x)}。

2 改进的双投影算法

算法1改进的双投影算法。

步骤0基本参数设置：设σ>0，μ∈(0，σ-1)，γ∈(0，1)。取x0∈C为初始点。计算

zk=PC(xk-μF(xk))。

步骤1计算rμ(xk)=xk-zk。若rμ(xk)=0，则停止；否则，转到下一步。

步骤2令mk为使得式(3)成立的最小正整数m，使

〈F(xk)-F(xk-γmrμ(xk))，rμ(xk)〉≤σ‖rμ(xk)‖2

(3)

成立。计算ηk=γmk，yk=xk-ηkrμ(xk)，并转到下一步。

(4)

在以后的所有分析中，我们总假设以下2个条件成立：

(A1)F：Rn→Rn是连续的； (A2)SD≠∅。

下面说明算法是有意义的。

命题1对每一个k∈N，总存在一个有限的非负整数mk使步骤2中的不等式成立。

证明若步骤2中的不等式不总是成立，则存在某个k0∈N使得对所有非负整数m都有式(5)成立：

〈F(xk0)-F(xk0-γmrμ(xk0))，rμ(xk0)〉>σ‖rμ(xk0)‖2。

(5)

对式(5)左端，当m→∞时，有γm→0，从而(xk0-γmrμ(xk0))→xk0。由条件(A1)和内积的连续性可得〈F(xk0)-F(xk0-γmrμ(xk0))，rμ(xk0)〉→0，即0≥σ‖rμ(xk0)‖2。又因为σ>0，故只有rμ(xk0)=0，与步骤1中rμ(xk0)≠0矛盾。

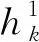
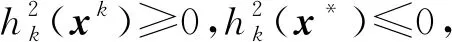
(6)

即

(7)

其中，第1个不等式由步骤2得到，第2个不等式由引理4得到。

另一方面，任取x*∈SD， 有

〈F(yk)，yk-x*〉≥0， ∀yk∈C。

(8)

故有

(9)

‖rμ(xk)‖2-μ〈F(xk)，rμ(xk)〉+〈F(yk)，rμ(xk)〉≥

‖rμ(xk)‖2-μ〈F(xk)，rμ(xk)〉+〈F(xk)，rμ(xk)〉-σ‖rμ(xk)‖2=

(1-σ)‖rμ(xk)‖2+(1-μ) 〈F(xk)，rμ(xk)〉≥

(1-σ)‖rμ(xk)‖2+(1-μ)μ-1‖rμ(xk)‖2=

(10)

〈xk-zk，x*-xk〉=〈xk-μF(xk)-zk，x*-zk〉+〈μF(xk)，x*-xk〉+

〈μF(xk)-rμ(xk)，rμ(xk)〉≤

〈μF(xk)-rμ(xk)，rμ(xk)〉。

(11)

和

(12)

故目标不等式可由式(11)与式(12)相加，再整理得到

(13)

进一步，由式(13)得

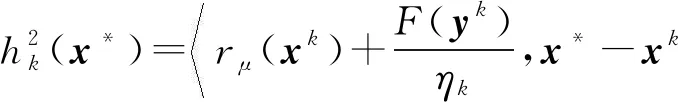
(14)

命题3若SD≠∅，则步骤3一定成立。

3 收敛性分析

在条件(A1)和(A2)成立的情况下，若序列{xk}是由算法1所产生的有限序列，则存在k0∈N，使得rμ(xk0)=0，故xk0为变分不等式(1)的一个解，否则产生的序列为无穷序列。接下来的讨论中均假设序列{xk}是由算法1所产生的无穷序列。

证明由于xk+1=PCk(xk)，则，

(15)

即,

(16)

(17)

由F(x)和投影算子的连续性可得序列{zk}有界，进一步序列{yk}和序列{rμ(xk)}有界。

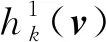
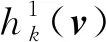
ζ‖x-y‖<‖〈F(yk)，x-yk〉-〈F(yk)，y-yk〉‖=
‖〈F(yk)，x-y〉‖≤‖F(yk)‖‖x-y‖。

(18)

但‖F(yk)‖>ζ与序列{yk}有界矛盾。

定理2若SD≠∅，则由算法1所产生的无穷序列{xk}收敛到变分不等式(1)的一个解。

证明根据Ck的定义，可得

(19)

由式(17)得

(20)

由引理5、命题4、定理1和式(7)知

(21)

接下来分2种情况讨论：

〈F(xk)-F(xk-γmk-1rμ(xk))，rμ(xk)}>σ‖rμ(xk)‖2。

(22)

由F(x)和rμ(x)的连续性，可令式(22)k→∞，得

(23)

4 数值实验

本章用2个数值实验来测试算法1，并将其与参考文献[16]的算法进行比较。 使用MATLAB版本7.1.0.246(R14)Pack3，其中包含优化工具箱3.0版本和惠普笔记本(CPU：intel i5-4200M)。 本文将以文献[16]中2个典型例子来说明算法的有效性。选取10-4作为停机准则，即当‖r(x)‖≤10-4时，程序终止。参数均来自于算法1且某些参数的选取与文献[16]一样，即仍选取σ=0.99，γ=0.4，另外μ=1。本文参数μ的其他取值结果以及当空间维数较高时的解，为了方便，将其省略。用以下2个典型例子说明算法1的有效性。例1是一个拟单调变分不等式的推广，例2是一个仿射变分不等式。

例1设变分不等式(1)中C=[-1，1]，F(x)=x2。 选取不同的初始点， 对算法1进行测试，结果如表1。

表1 算法1测试-1

例2令变分不等式(1)中C=[0，1]n，F(x)=Mx+d，其中

选取初始点x0=(1，1，…，1)T，然后分别在不同的维数下进行试验，结果见表2。

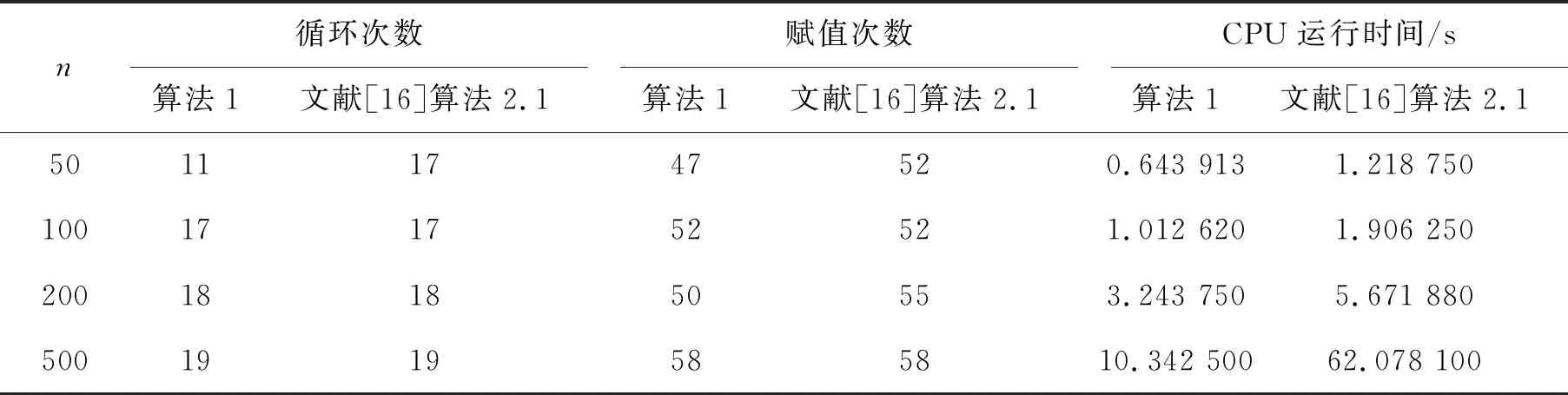
表2 算法1测试-2

上面2个数值实验不仅表明算法1是有效的，而且表明对某些参数，算法1比文献[16]中的算法收敛更快。