意料之外的收获———由一道典型题所引发的思考

李兴玉 苏明山

近段时间,在引导学生复习总结动量守恒定律专题知识时,一位物理成绩很不错的学生就一道例题提出了一个让笔者颇感意外的问题．之所以感到意外,一是这道题是一道再常见不过的题,平时多有涉及,其解题方法对大部分学生来说可谓耳熟能详;二是他提出的问题是笔者一直认为理所当然,无须解释和证明的．但经过思考和讨论发现,这些我们认为“理所当然”或“有意回避”的问题,值得我们深入探讨．

1 意料之外的问题

图1

A. 1∶2 B. 1∶3 C. 1∶6 D. 1∶9

本题思路清晰,求解方法明确,对一般的学生而言,属于容易题．针对本题,学生提出的问题剑走偏锋,让人始料未及．他提出的问题是:为什么物块向上的速度为零,即物块沿圆弧轨道上升到最高点时,物块和圆弧轨道在水平方向具有相同的速度.

2 解决问题的三种方法

2.1 类比追及相遇问题

类比法是通过对两个或两类研究对象进行比较,找出它们之间的相同点或相似点,并以此为根据把其中某个或某一类对象的有关知识和结论,迁移到另一个或另一类对象上，从而推出它们也可能有相同或相似结论的一种逻辑推理和研究方法．采用类比的方法,可使复杂的问题简单化,对学生而言,有时候更能说清楚问题．物块在圆弧轨道上滑动的过程,可类比直线运动中的追及相遇问题,在水平方向上,物块未上升到最高点之前,相对于圆弧轨道向右运动,物块上升到最高点之后,相对于圆弧轨道向左运动．最高点是二者在水平方向相对运动的转折点,类似于追及相遇问题中的“最近距离”,故可推断当物块向上的速度为零时,物块和圆弧轨道在水平方向具有相同的速度．

2.2 寻找关联速度

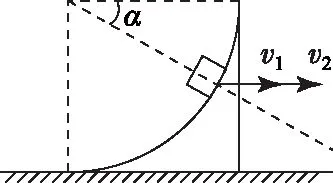
图2

高中物理涉及的关联速度主要有绳系关联、杆系关联和面接触关联.其中面接触关联介绍得较少,对于面接触关联的两运动物体，它们在垂直接触面方向分速度相等．寻找在不同条件下,运动物体间速度的关联关系,往往是分析物理问题的切入点,以此角度审视学生提出的问题,亦可得到合理的解释．物块和圆弧轨道运动的过程中,虽然物块在圆弧轨道上的位置不断改变,但二者在垂直于接触面方向,即沿圆弧半径方向无相对运动．如图2所示,当物块向上的速度为零时,物块和圆弧轨道的速度v1、v2在沿圆弧半径方向的分速度相等,即v1cosα=v2cosα,可知v1=v2．

2.3 利用数学推导

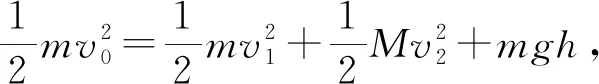
其实,日常教学中,学生提出的类似问题有很多,这些问题从教师的角度审视时,很难被发现,而当个别学生提出时,又多被教师以“显而易见”为理由搪塞过去．日积月累,由于这些细节问题给学生所造成的困顿,使学生分析问题、解决问题的思维能力难有质的飞跃,这也是学生刷题刷出的“唯手熟尔”,却知其然而不知其所以然的原因所在．“问渠哪得清如许,为有源头活水来.”作为教师,要时刻站在学生的角度思考问题,关注问题的细节,审视自己的教学,在授业的同时,更应该解惑.只有这样,才能真正促进学生知识的内化,引得源头活水来,有效提升学生分析问题、解决问题的能力．