巧用轨迹圆的圆心轨迹求解带电粒子在磁场中的运动问题
2020-06-11路文柱
高中数理化 2020年2期
路文柱
带电粒子在磁场中的运动问题的解题步骤包括定圆心、求半径、作轨迹、找几何关系等,其中首先要确定带电粒子运动轨迹的圆心.确定带电粒子运动轨迹的圆心通常有两种方法,一是利用速度的垂线,二是利用弦的中垂线.当粒子的入射速度大小确定而方向不确定(分布在一个夹角范围)时,每个方向进入的带电粒子运动轨迹的圆心是不同的,但只要入射粒子的轨迹半径相同,这些圆心到入射点的距离就相同,它们的连线就构成了一个新的圆或圆的一部分(如图1),我们把它叫作轨迹圆的圆心轨迹.巧妙利用轨迹圆的圆心轨迹可快速准确地找出沿任意方向进入磁场的带电粒子在磁场中运动轨迹的圆心,进而求解带电粒子在磁场中的运动问题.

图1

图2

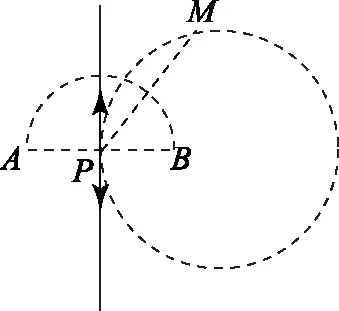
图3

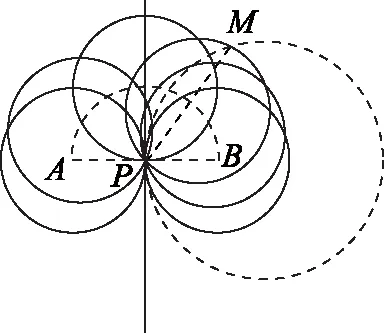
图4
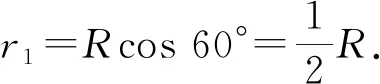

图5 图6
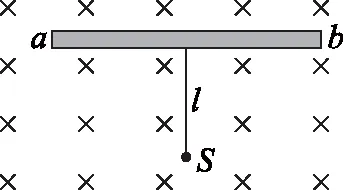
图7



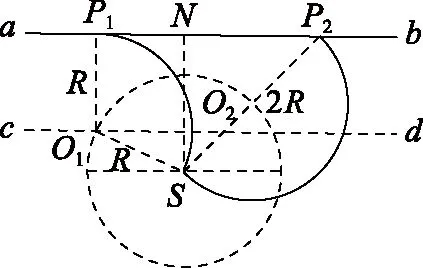
图8
再考虑N的右侧.任何α粒子在运动中离S的距离不可能超过2R,以2R为直径、S为圆心作圆弧,交ab于N右侧的P2点,P2点与S的连线跟轨迹圆的圆心轨迹的交点O2即为过P2点的运动轨迹的圆心.P2点即右侧能打到的最远点.由图中几何关系得
所以ab板上被α粒子打中区域的长度为
P1P2=NP1+NP2,
代入数据解得P1P2=20 cm.
可见,轨迹圆的圆心轨迹对求解以相同速度沿不同方向进入磁场的带电粒子的运动问题有很大帮助.
