蒙特卡罗模拟优化CRKP感染时美罗培南的给药方案
2020-06-08王小庆
操 玮,王小庆,李 丽
0 引言
肺炎克雷伯杆菌(Klebsiellapneumoniae,KP)是条件致病菌,也是医源性严重感染的常见病原菌之一,耐药趋势逐年递增,耐碳青霉烯类肺炎克雷伯杆菌(CarbapenemresistantKlebsiellapneumoniae,CRKP)成倍增长,而且抗药性强。制定耐药肺炎克雷伯杆菌感染的给药方案成为临床医生棘手的难题。国外研究者通过计算机模拟,能够预测不同给药方案的达标率,为临床制定方案提供客观依据。本文采用蒙特卡罗模拟法(Monte Carlo simulation,MCS),根据药物的不同药代动力学模型公式、相关参数随机值,通过计算机模拟计算,预测不同给药方案的达标率。
1 资料与方法
1.1 给药方案 美罗培南按照某三甲医院常用剂量1~4 g/d给药,给药频次和单次剂量见表1。
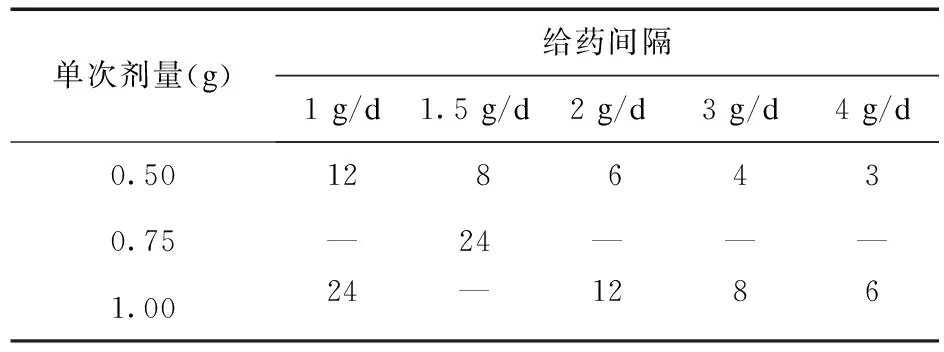
表1 美罗培南给药方案(h)
1.2 最小抑菌浓度 某三甲医院微生物室利用K-B纸片法KP进行药敏试验,结果根据CLSI 2015年标准判断[1],最小抑菌浓度(Minimum inhibition concentration,MIC)范围大于8判定为耐药。2016-2018年我院检出20例CRKP,微生物室提供的MIC值为8~16。
1.3 统计方法 美罗培南属于时间依赖性抗菌药物,此类药物给药目标是尽量延长药物浓度超过MIC的时间。参阅说明书和相关文献确定美罗培南药代动力学参数值,公式中的相关参数意义如表2,以表1的给药方案预算%ft>MIC,设定%ft>MIC的靶目标达到90%,理论上可以有效杀菌,达到100%可获得最大杀菌速率。
按一室模型计算时间依赖性的美罗培南的%ft>MIC公式如下[2-3]:
%ft>MIC=ln[Dose×f/(Vd×MIC)]×t1/2×0.693-1×r-1×100%
%ft>MIC={TINF-ln[Ro÷CL÷(Ro÷CL-MIC)]+ln(Ro÷CL)-ln(MIC)}×(t1/2÷0.693)×100/DI
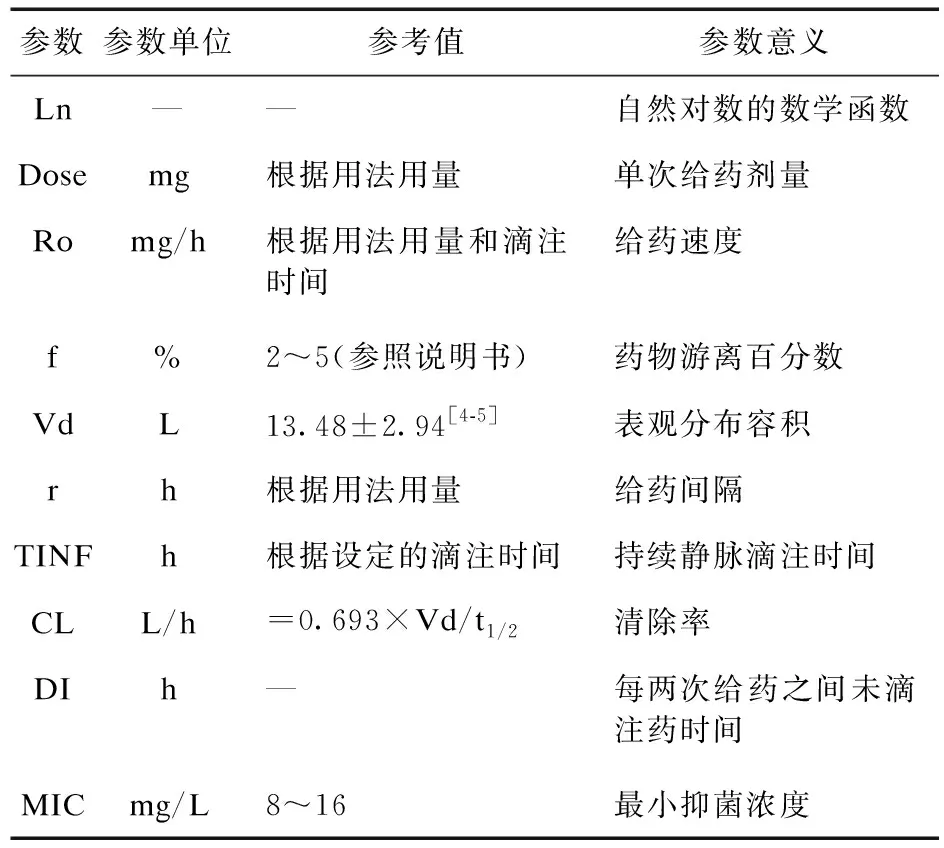
表2 公式中美罗培南药代动力学参数和给药方案中的相关参数
本文用水晶球软件,假设MIC服从离散均匀分布,f服从随机均匀分布[2],其他药动学参数均服从正态分布,采用MCS,设定模拟预设的次数,预测目标获得率(Probability of target attainment,PTA)或达到设定目标累积反应分数(Cumulative fraction of response,CFR),能达到>90%的PTA或CFR的给药方案为优选方案[2]。
2 结果
2.1 给药剂量和频次优化 按照表1给药方案,按照公式1模拟耐药菌给药方案,见图1。结果显示,10种给药方案CFR均未超过90%,其中0.5 g (q3h)和0.5 g (q4h)给药方案有%ft>MIC>90%的可能性,但CFR分别是4.85%和29.52%,未达到90%。
2.2 持续静脉滴注时间优化 结果可能达到目标值的0.5 g (q3h)和0.5 g (q4h)给药方案,持续静脉滴注0.5、1、2、2.5、3 h,按照公式2模拟给药方案,如图2和图3结果,0.5 g (q3h)、0.5 g (q4h)给药方案持续静脉滴注2、2.5、3 h,%ft>MIC>100%的CFR达到100%。
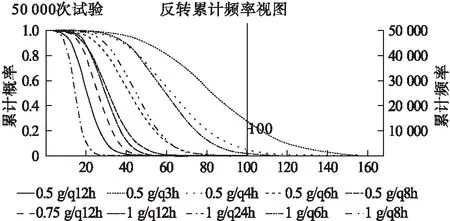
图1 不同给药方案CFR对比(图例按CFR由低到高顺序排列)
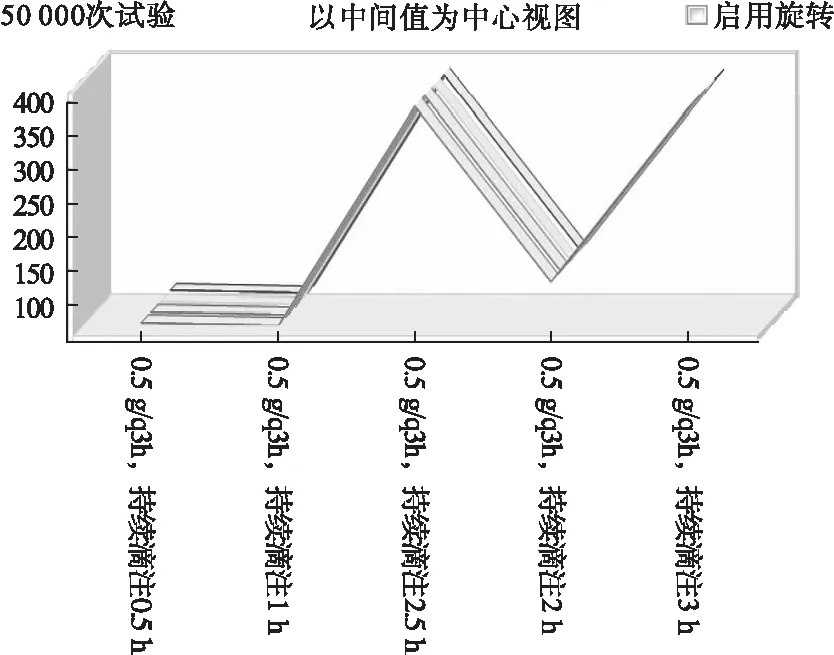
图2 给药(0.5g/q3h)持续滴注时间不同%ft>MIC趋势图
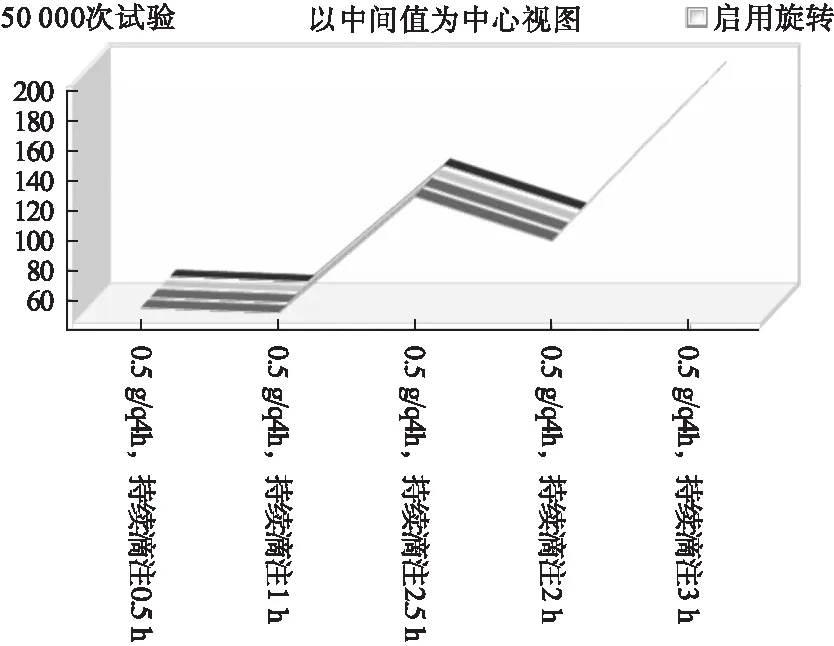
图3 给药(0.5g/q4h)持续滴注时间不同%ft>MIC趋势图
2.3 公式模型参数敏感性分析 模型中涉及参数敏感性分析如表3,%ft>MIC影响因素包括MIC、Vd和半衰期,MIC和半衰期影响最大;MIC和Vd造成负相影响,半衰期造成正相影响。
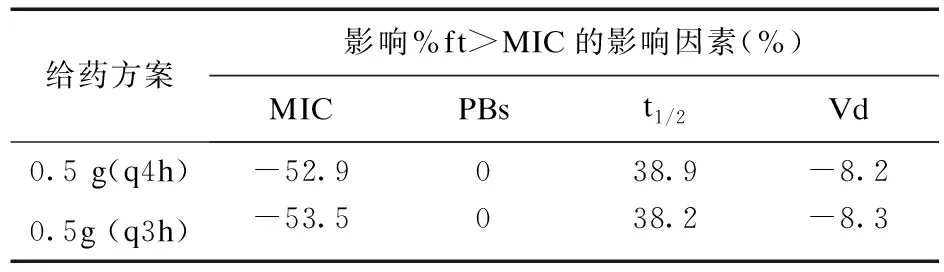
表3 PK/PD参数敏感性分析
3 讨论
中国细菌耐药监测网(CHINET)公布的数据表明CRKP呈上升趋势,在 ICU 及呼吸内科发生耐药的几率较高[6]。2015-2018年我院检出20例CRKP。临床医生和药师协作优化抗菌药物给药方案,可以提高治疗有效率,降低病死率,防止细菌耐药[7],同时减少不良反应发生的风险。
3.1 给药方案评价与优化 美罗培南属于时间依赖性抗菌药物,以%ft>MIC的指标大于40%~50%为目标治疗肺炎克雷伯杆菌敏感菌,MIC值为8是肺炎克雷伯杆菌耐药折点,以%ft>MIC高于90%临床上可获得有效抗菌效果,大于100%临床上可获得最大治疗效果。本文通过药代动力学模型一对给药剂量和频次进行优化,10种给药方案模拟预测美罗培南不同给药方案治疗CRKP感染的CFR或PTA,只有0.5 g (q3h)和0.5 g (q4h) 2种存在PTA可能达到靶目标的给药方案,模拟结果中有%ft>MIC大于90%,但CFR只有4.85%和29.52%,说明达到靶目标的概念率较低,预测治疗有效率较低。
根据剂量和给药频率优选结果,药代动力学模型二对持续滴注时间模拟,静脉滴注时间持续0.5、1 h的CFR不到50%,输液时间在2、2.5、3 h的CFR或PTA超过90%,预测可以达到治疗效果,与文献报道资料结论相符[8-9]。
通过本方法,按时间依赖性抗菌药物的特点模拟出给药方案,对于CRKP感染患者可以参照方案尽早给药,根据治疗效果再次评估调整方案。本文主要参照美罗培南在正常人体内的药代动力学参数,MIC参照血液培养,未考虑其他组织感染可能因渗透性不足导致与血液中浓度的差距。在实际应用中还要考虑其他影响药代动力学参数的其他因素,如年龄、基础疾病、体重以及其他治疗(如是否透析以及合并用药等),考虑增减剂量和调控速度,有条件的医院可以参照血药浓度监测结果及时调整方案,若治疗效果不佳或混合感染还要考虑是否联合用药。
3.2 公式模型的参数影响 PK/PD参数决定抗菌药物能否在感染部位达到有效浓度及治疗作用,通过模拟预测覆盖有效MIC的时间百分比,提高临床用药科学性和合理性。模型中的参数是正常人PK/PD的参考值,理想的参数应为患者特殊群体的参数或考虑个体差异。如:严重脓毒症患者表观分布容积的改变,病原菌侵袭感染部位及毒力作用,局部组织灌流不足,若患者同时接受肾脏替代治疗,其美罗培南Vd和清除率增加,可使美罗培南谷浓度降低至靶浓度以下,因此,可能需要增加美罗培南的剂量[10]。对于感染了高MIC值病原菌的严重感染患者,目标值甚至需要达到100%,目标靶值设定为100%,杀菌活性更强,能很好地预测其临床治愈率和细菌清除率。
3.3 关于MCS MCS于20世纪40年代应用于科学领域,90年代用于指导抗菌药物使用,而且其可行性已被证实。MCS可以预测50 000名“患者”的实验结果,易操作、速度快,同时也节省人力物力,为临床指导抗菌药物合理应用提供客观依据。本文仅做了美罗培南延长输注时间的模拟,还可以借助其他药物的数学模型公式,对其他药物进行模拟,为患者选择给药方案。
目前,国内不同群体患者美罗培南的群体药动学模型尚未建立,使用的是健康人群的随机参数,预测结果仅可能作为初始给药方案的参考,在临床实际应用中,需要根据给药后的治疗效应以及使用后的实际谷、峰浓度等调整给药方案。
