超声导波在杆件中传播时的频散特性

2020-06-07张佳凯

工程与建设 2020年6期

张佳凯

(合肥工业大学土木与水利工程学院，安徽合肥 230009)

0 引言

超声波在有限空间的固体中传播的时候,会不断地反射并形成复杂的叠加干涉即导波。超声导波在固体中的传播相比光的传播速度还是很慢的,因此本文不考虑相对论效应,仍然认为它是一种宏观低速的运动。

利用超声导波监测钢杆损伤是弹性波动在固体中传播诞生的一种新兴的损伤识别技术。早在19世纪末,人们就注意到超声导波在板中的传播,最终,H.Lamb[1]求出了导波在薄板中传播的波动解,为了纪念他做的贡献,这个就被命名为Lamb波。1889年,Chree[2]在研究超声导波在无限长杆件中传播时发现,超声导波会出现不同的模态,有纵向模态、扭转模态和弯曲模态,并给出了各自的频率方程,然而由于这个方程属于超越方程,无法得出解析解。终于在1973年,Pochhammer[3]运用数值方法求解出来。1998年,英国帝国理工大学的M.J.S.Lowe和P.Cawley等开发出了一款可以快速绘制各类导波的频散曲线的MATLAB程序[4],极大地提高了人们检测的效率。超声导波一直在发展,特别是近年来在国内发展很快[5],因此在理论上进一步研究导波在杆件中的传播特性很有必要。

1 超声导波的基本介绍

声波是在正常情况下人能听到的声音,它的频率一般处在20～20 000 Hz。超声波是指频率大于20 000 Hz的波,人不能听到。超声在传播的过程中根据环境条件的不同分为两种情形:一种是波在传播过程中不受到边界的限制——波在介质中传播时总接触不到环境的边界或者环境是理想的无限大空间,这种波称为体波;另一种是波在传播的过程中会受介质边界的限制——波在较小的环境中传播,总是会遇到障碍(环境中存在却也不一定都存在边界,它的某个自由度上可能是无限大的空间)并在边界处散射或反射,这种波称为导波。

导波在传播时,或是受边界的影响,抑或是受介质的影响,波的性质可能改变,或是波的传播方向改变。在这种情形中,导波由原来的单一的恒定的波形变成了由多股不定模态和传播方向的波形,这种情况我们称为波的频散。

频散描述的是波传播的速度随着频率的变化而发生变化的关系;在声学领域,波的频散是指某一固定的、单一的频率的波在传播时分化出几种不同频率波。不同性质的材料会有不同的表现:能够产生频散的材料属于色散材料,不发生频散的材料属于无色散材料。凡是发生频散时,波的相速度、群速度总和波的中心频率、波数密切联系在一起。

2 波的类型与描述

波的类型主要有体波和面波,在整个弹性体传播的是体波,比如纵波、横波。而沿着两种不同介质的分界面传播的波被称为面波,如瑞利波和勒夫波,它的能量大致集中在分界面附近的范围内,并且它的能量不向传播路径上的介质传播,而且它的形成是因为体波在介质中相长干涉形成的。当波从起始点处向远处传播时,它的振幅会随着传播距离的增加而减小,这种衰减被称为几何或辐射衰减。当波在传播时因为材料的阻尼而导致的衰减被称为材料衰减。当波因为在介质交界面反射而导致的衰减被称为表观衰减。有许多的速度描述波在传播过程中的特性,下面主要介绍其中三种速度:相速度、群速度和能流速度。

2.1 相速度

波的相位变化的速率就称为相速度,也就是波相位的传播速度;单一频率的波的速度就是相速度。下面用图1介绍相速度的概念。

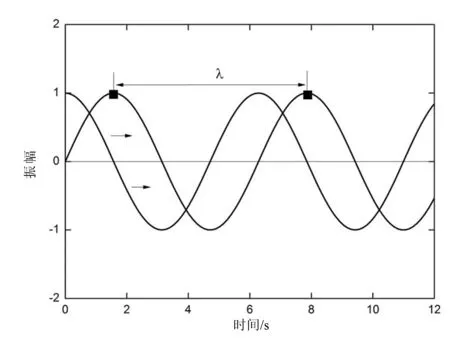
图1 同相位点传播速度

相同的相位点在单位时间内传播的距离称为相速度。可得到相速度cp、周期T和波长λ的关系有:

(1)

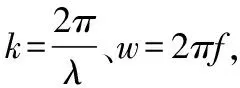
(2)

式中:cp为相速度;w为用圆频率;k为波数。

在无色散介质中,用相速度就可以描述波的传播速度,但是在有色散介质中,仅用相速度就不能全面地描述波的传播速度问题了。本文引入群速度来一起描述。

2.2 群速度

由一群不同频率的波组成的在材料中一起传播的速度,也就是一群波合成的波向前传播的实际速度。从能量的角度看,就是这群波合成的能量一齐向前传播的速度。下面,本文用两个振幅相同,频率、波数略有不同的正弦波沿着相同的方向传播的例子来进行说明。两个波相互叠加后如图2所示。

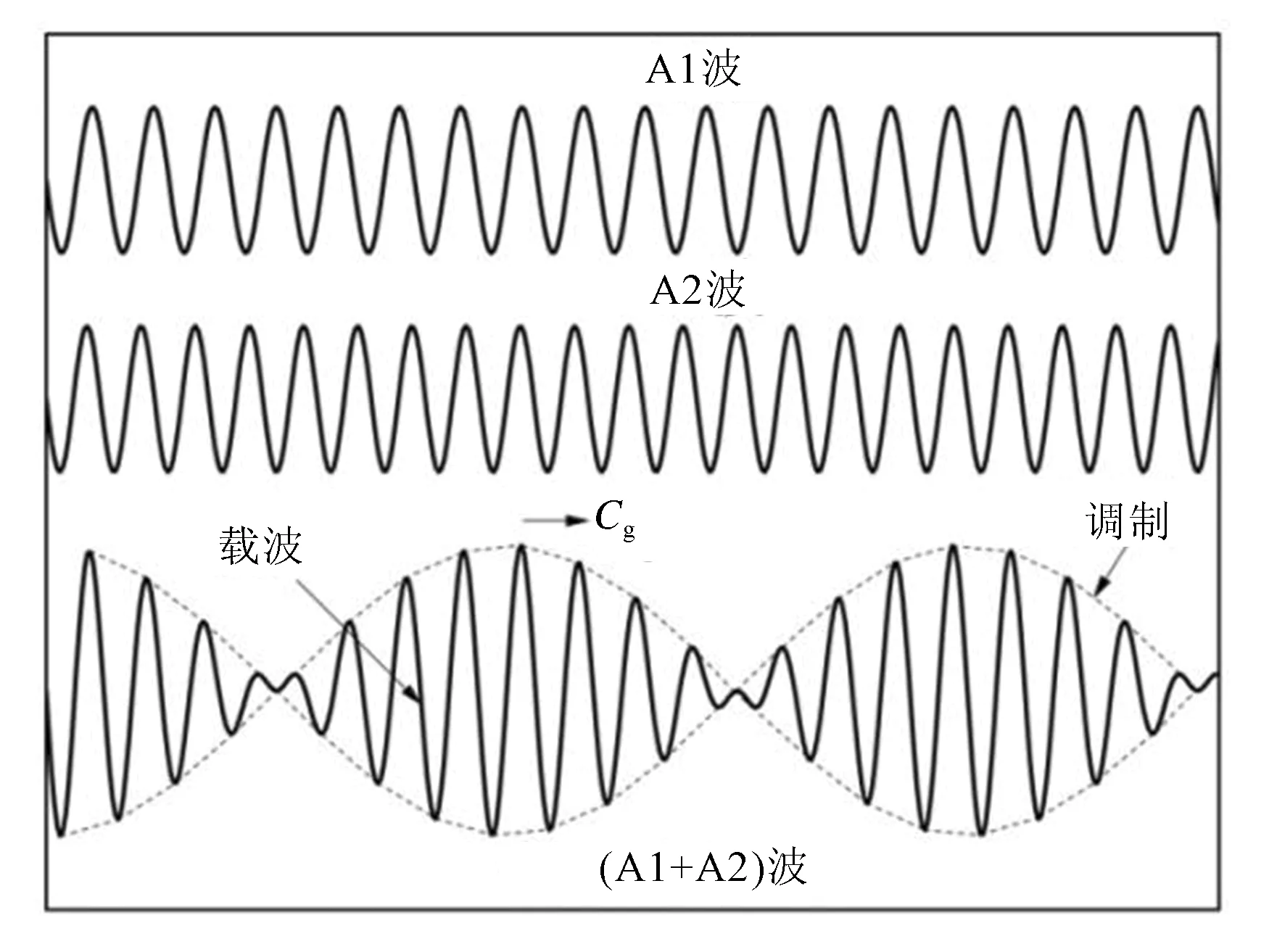
图2 波的叠加

两波叠加后的振幅为:

u=A[sin(ω1t-k1x)+sin(ω2t-k2x)]

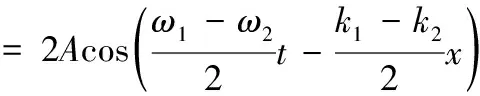
(3)

u=C(x,t)sin(ω0t-k0x)

(4)

其中

C(x,t)=2Acos(Δωt-Δkx)

(5)

“振幅因数”C(x,t)称为调制,sin(ω0t-k0x)为载波,上式表示一个波群包络线,它以群速度cg传播,令

Δωt-Δkx=常量

(6)

求导得:

(7)

取极限,得到群速度传播的公式,也就是这列波能量的传播速度:

(8)

2.3 杆状固体中导波的传播

2.3.1 弹性体的运动方程

根据弹性力学的平衡微分方程,在运动微分方程中除了要考虑应力和体力外,还要考虑惯性力,根据达朗贝尔原理,每体积弹性体上惯性分量分别为:

柱状坐标更适合表示杆,因此我们用柱状坐标代替直角坐标下的运动微分方程,有Navier控制方程[6]:

(9)

(10)

(11)

式中：ur、uθ、uz分别为圆柱的径向、环向、轴向位移;ωz、ωr、ωθ为旋转矢量的三个分量;λ为拉梅常数;μ为泊松比;φ为柱坐标下体积不变量;r为柱半径;θ为圆柱截面夹角。

(12)

(13)

(14)

根据胡克定律,在杆状固体的表面有边界应力σrr,σrθ,σrz满足:

(15)

(16)

(17)

杆位移可以从杆的边界条件推出:

ur=U(r)cosnθei(kz-ωt)

(18)

uθ=V(r)sinnθei(kz-ωt)

(19)

uz=Wrcosnθei(kz-ωt)

(20)

式中：n是自然数。

2.3.2 杆中导波传播的纵向模态

当应力波在杆中传播时,圆杆上各个点的位移关于中心轴对称,即仅有ur、uz存在,uθ为零。纵向传播模态如下图3所示。

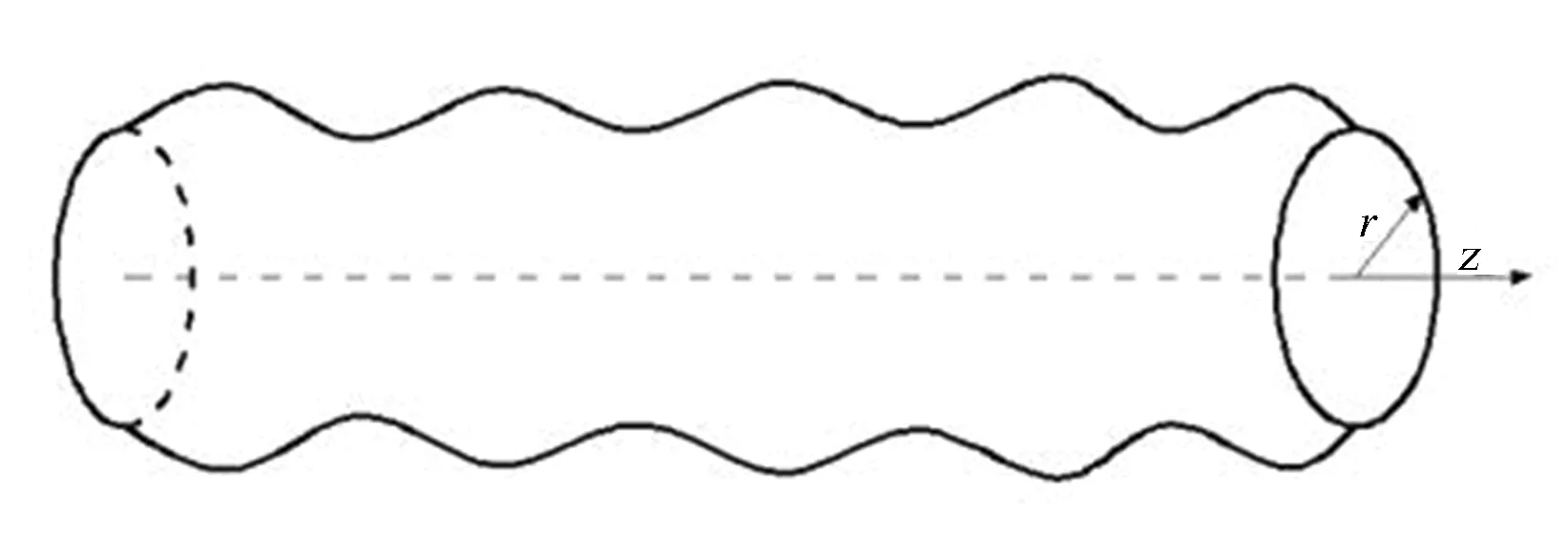
图3 波传播时的纵向模态

波传播时纵向模态的频率方程:

-(β2-k2)2J0(αa)J1(βa)

-4k2αβJ1(αa)J0(βa)=0

(21)

其中,

式(21)就是大名鼎鼎的Pochhammer方程。该方程在1876年就第一次被发表出来了,然后由于方程中存在两个相互独立的未知数k和f,因此并不能得到精确的解析解,再加上由于当时数值计算能力的落后,直到1940年该方程才被解开。由此可以看出,一项技术的发展可以带动其他领域的发展。

2.3.3 杆中导波传播的扭转模态

应力波的扭转模态如图4所示,此时径向位移和轴向位移为零,只有环向位移uθ存在。

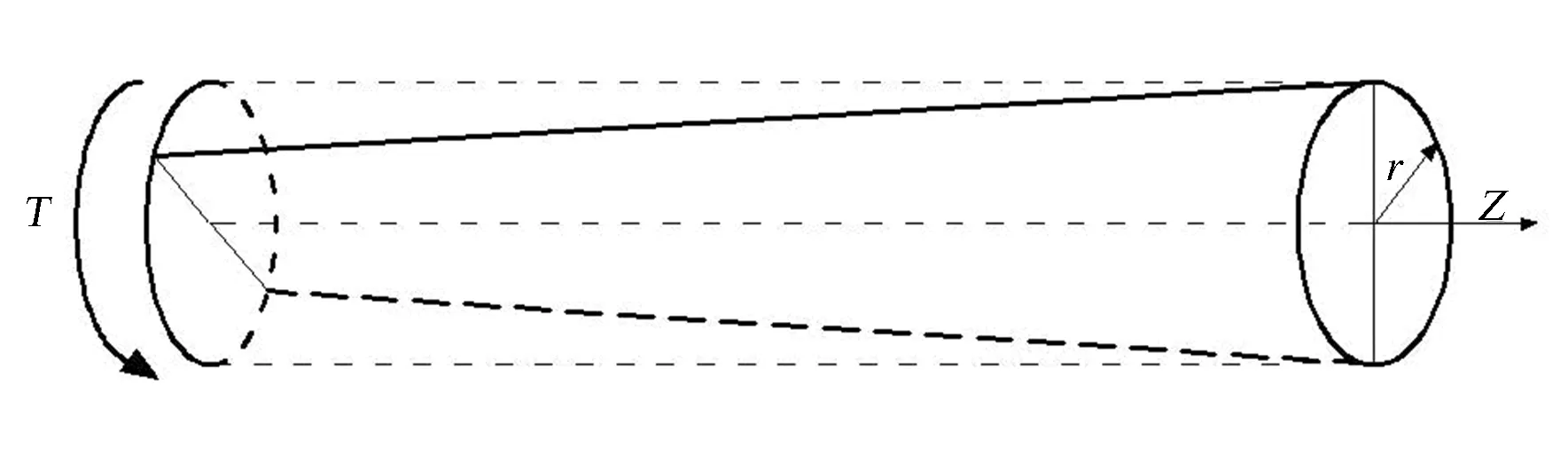
图4 波传播时的扭转模态

波传播时扭转模态的频率方程为:

(βa)J0(βa)-2J1(βa)=0

(22)

2.3.4 杆中导波传播的弯曲模态

应力波在杆中的弯曲模态如图5所示,这种模态比较复杂,一般研究n=1时的模态,即F(1,m)模态。

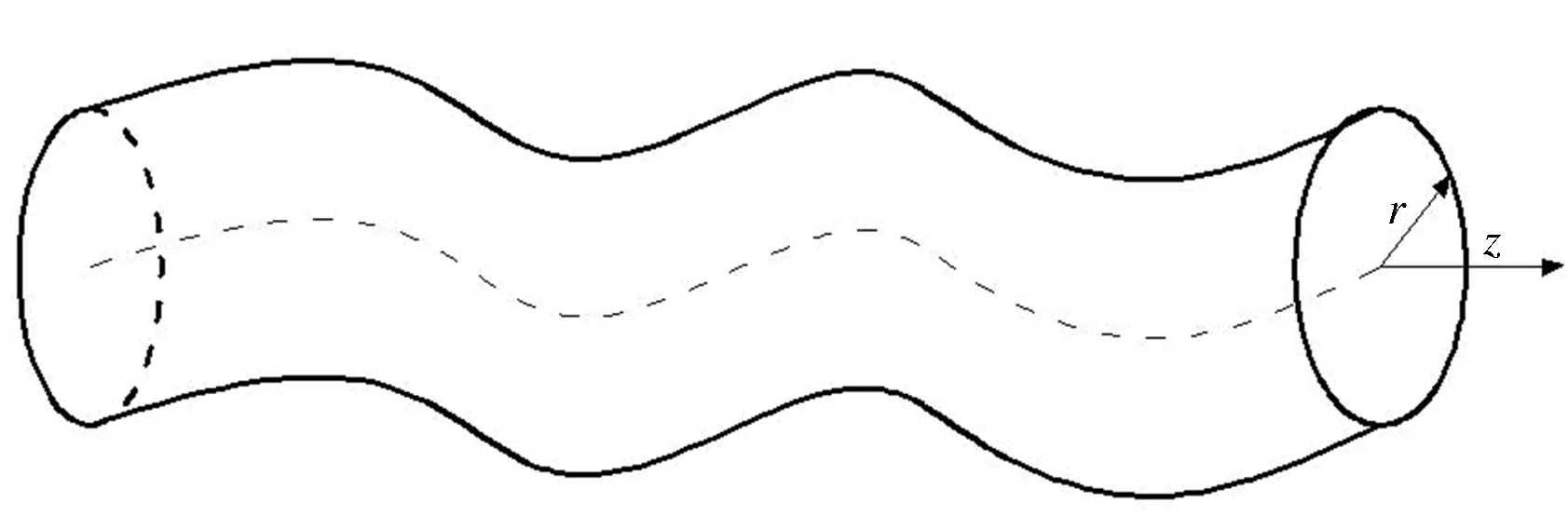
图5 波传播时的弯曲模态

波传播时弯曲模态的频率方程为:

(23)

2.4 钢杆的频散曲线

2.4.1 频散曲线的绘制

已知钢杆(图6)的弹性模量E=210 GPa,密度ρ=7 860 kg/m3,泊松比ν=0.3,半径d=4 mm。

图6 钢杆示意图

将上述参数带入到频率方程,用MATLAB数值求解频散方程,主要步骤如下:

(1) 令k=0求出当k=0时满足方程的f值,这里得到的f值即为模态对应点的截止频率;

(2) 取f值的范围在0～1 000 kHz,求出每一个f值下满足频散方程的k值;

(3) 将得到的f值和k值组合,并将它们绘制出来,就得到了频率和波数的关系图,如图7所示为纵向模态下的频率和波数的关系,这里只画出了前5阶的模态。

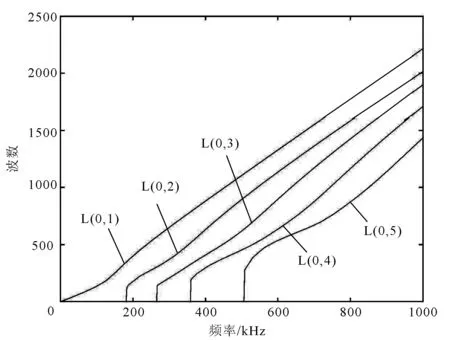
图7 纵向模态频率和波数的关系

2.4.2 不同频率下钢杆中导波的相速度

重复上节关于频散方程的求解,利用各个模态的频率方程,利用MATLAB软件可以绘制出不同模态下、不同频率下钢杆中导波的相速度,如图8所示是直径为20 mm的钢杆中导波相速度的频散曲线。

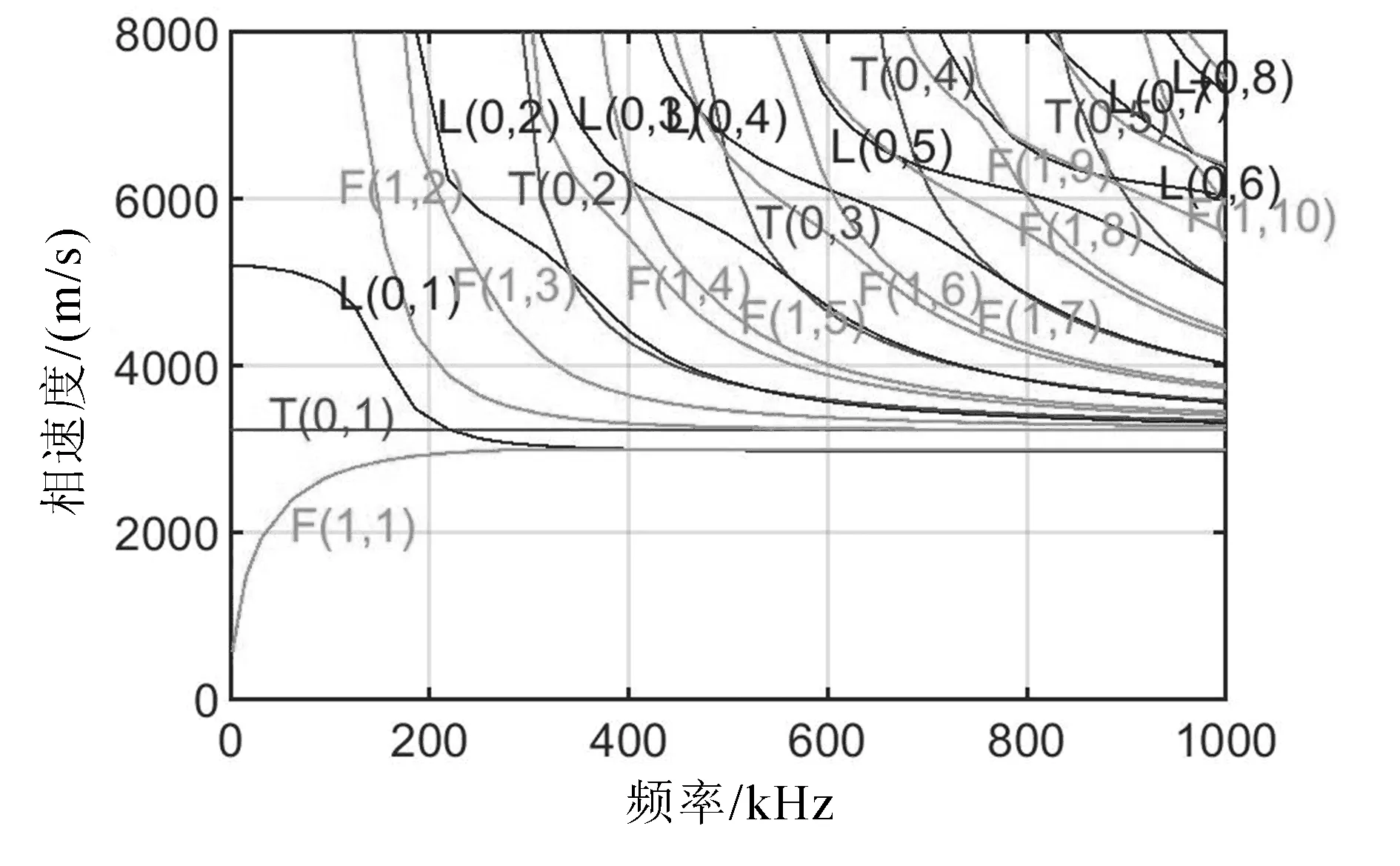
图8 不同频率下钢杆中导波的相速度

从图8可以看出:各个模态的相速度随频率变化的趋势大体一致,但也有例外。如T(0,1)的相速度就不会随着频率的改变而改变,是个恒量;其他模态的相速度都是随着频率的增加而逐渐降低到趋于一定的值,而F(1,1)是随着频率的增加而增加到趋于一定的定值。

与其他模态的出现要高于一定的截止频率不同,L(0,1)、F(1,1)和T(0,1)在0～1 000 kHz的范围内始终存在。

2.4.3 不同频率下钢杆中导波的群速度

下面利用MATLAB软件求解各个模态的频率方程,绘制不同模态下、不同频率下钢杆中导波的群速度,如图9所示是直径为20 mm的钢杆中导波群速度的频散曲线。

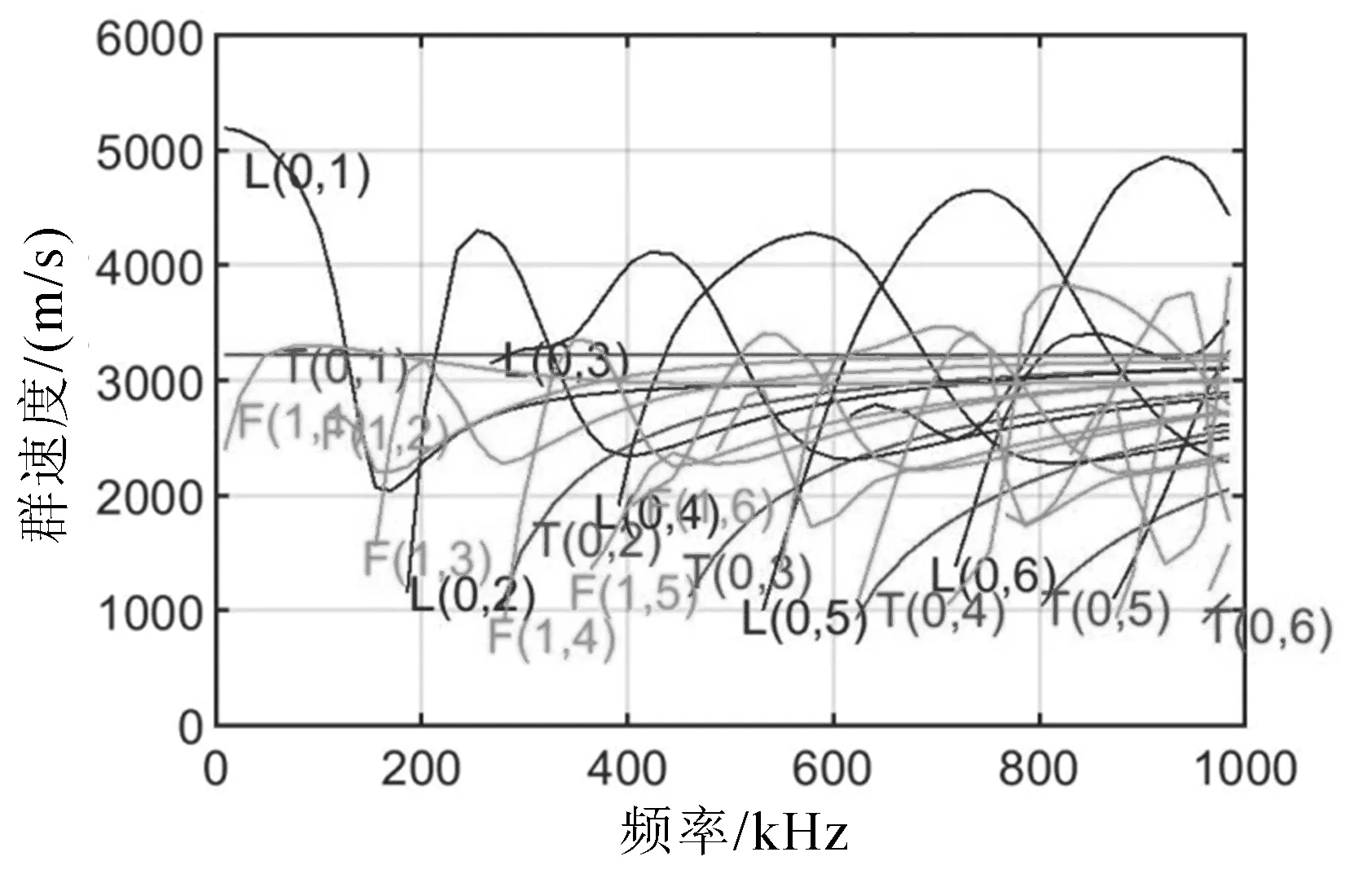
图9 不同频率下钢杆中导波的群速度

从图9可以看出:纵向模态L(0,m)和弯曲模态F(1,m)的群速度随着频率变化的趋势大体一致,而扭转模态T(0,m)则表现出不一样的趋势,除了T(0,1)的群速度不随着频率的改变而改变,其他扭转模态的群速度随着频率的增加而增加并趋于一定值。同时,有着相同趋势的纵向模态L(0,m)和弯曲模态F(1,m)也有明显的不同之处,L(0,1)的群速度是先减小后增加到一个稳定的值,F(1,1)的群速度是先增加再逐渐减小到一个稳定的值。

同样,与其他模态的出现要高于一定的截止频率不同,L(0,1)、F(1,1)和T(0,1)在0～1 000 kHz的范围内始终存在;从图9可以看出,在0～112.9 kHz的范围内,模态数量最少,只有L(0,1)、F(1,1)和T(0,1)三个模态存在,在这个频率范围内,导波传播的方式相对简单,适合用于监测。