导数破最值 参数巧求解
——2019年全国Ⅲ卷理科第20题
2020-06-06邓超群
邓超群
(湖北省襄阳市第三中学 441000)
在解决有关函数的最值问题时,经常采用导数法,结合导数运算、函数的单调性、函数的极值以及端点处的函数值的大小等来综合处理,最终得以解决有关函数的最值问题,是应用比较广泛的一类解题方法.而参数取值的确定问题是函数最值中的一类难点,属于逆向探究题型.解决的基本方法是待定系数法,从逆向思维出发,实现由已知向未知的转化,转化过程中通过列表或分类讨论,直观形象,结合最值,问题最终落脚在比较极值与端点值大小上,从而解决问题.
一、真题在线
高考真题(2019·全国Ⅲ卷理·20)已知函数f(x)=2x3-ax2+b.
(1)讨论f(x)的单调性;
(2)是否存在a,b,使得f(x)在区间[0,1]的最小值为-1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由.
本题(2)中有关含有参数的函数的最值问题,通过逆向思维法,采用分类讨论,在参数a不同取值情况下,结合函数f(x)在对应区间的单调性确定极值,从而比较极值和端点处的函数值的大小,以及题目中对应最小值与最大值的已知量,比较分析来确定相应的参数值问题.从不同的角度分类讨论,会有不同破解过程,产生不同的解题方式.
二、一题多解
解析(1)f′(x)=6x2-2ax=2x(3x-a).

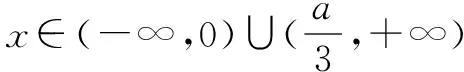
若a=0,则f′(x)≥0,即f(x)在(-∞,+∞)单调递增;
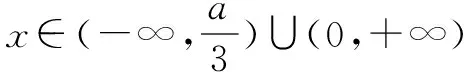
(2)方法1:(官方标答——参数分类讨论法)
满足题设条件的a,b存在.
①当a≤0时,由(1),知f(x)在[0,1]单调递增.
所以f(x)在区间[0,1]的最小值为f(0)=b,最大值为f(1)=2-a+b.
此时a,b满足题设条件当且仅当b=-1,2-a+b=1,即a=0,b=-1.
②当a≥3时,由(1),知f(x)在[0,1]单调递减.
所以f(x)在区间[0,1]的最大值为f(0)=b,最小值为f(1)=2-a+b.
此时a,b满足题设条件当且仅当2-a+b=-1,b=1,即a=4,b=1.
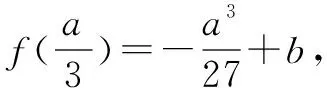
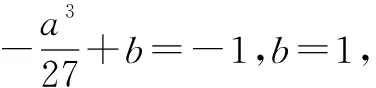

综上所述,当且仅当a=0,b=-1或a=4,b=1时,f(x)在[0,1]的最小值为-1,最大值为1.
点评借助(1)中函数f(x)的单调性情况,分“a≤0”,“a≥3”以及“0 方法2:(单调区间分类讨论法) 满足题设条件的a,b存在. 此时a,b满足题设条件当且仅当|f(1)-f(0)|=|2-a|=2,解得a=0或a=4. 则有a=0,b=-1或a=4,b=1. 综上所述,当且仅当a=0,b=-1或a=4,b=1时,f(x)在[0,1]的最小值为-1,最大值为1. 破解函数f(x)在闭区间[a,b](a 1.若所给的闭区间[a,b]不含有参数,则只需对函数f(x)求导,并求方程f′(x)=0在区间[a,b]内的根,并计算使导数等于零的根的函数值(可以一个,也可以多个),把这些函数值与f(a),f(b)的值进行比较,其中最大的一个值就是最大值,最小的一个值就是最小值. 2.若所给的闭区间[a,b]含有参数,在对函数f(x)求导的基础上,要通过对参数进行分类讨论,判断函数f(x)在各相应子区间内的单调性,利用单调性所对应的极值以及端点值的比较,从而得到函数f(x)的最值(最小值或最大值).
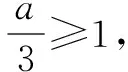

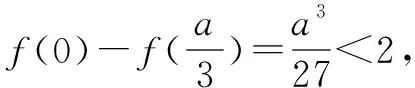

三、规律总结
