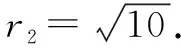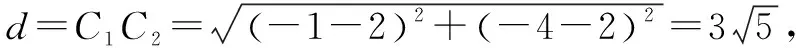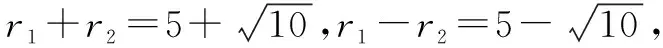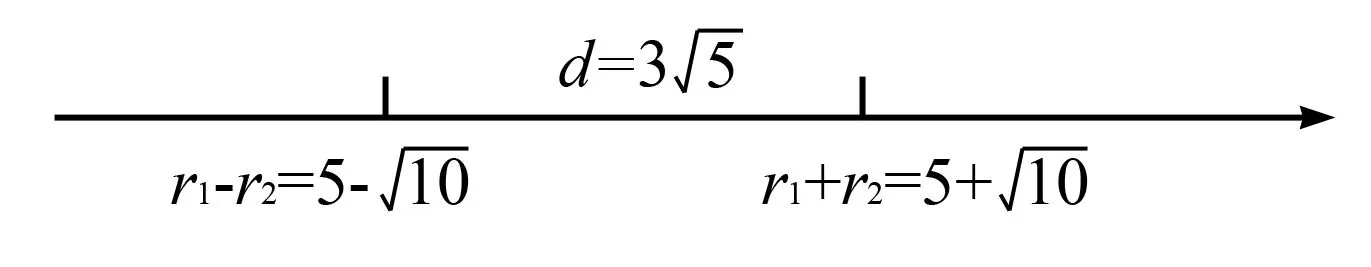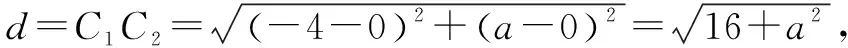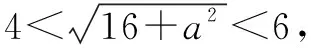巧用数轴表示圆与圆的位置关系
2020-06-06武兴亮
武兴亮
(江苏省无锡市青山高级中学 214000)
一、圆与圆的位置关系(几何法)
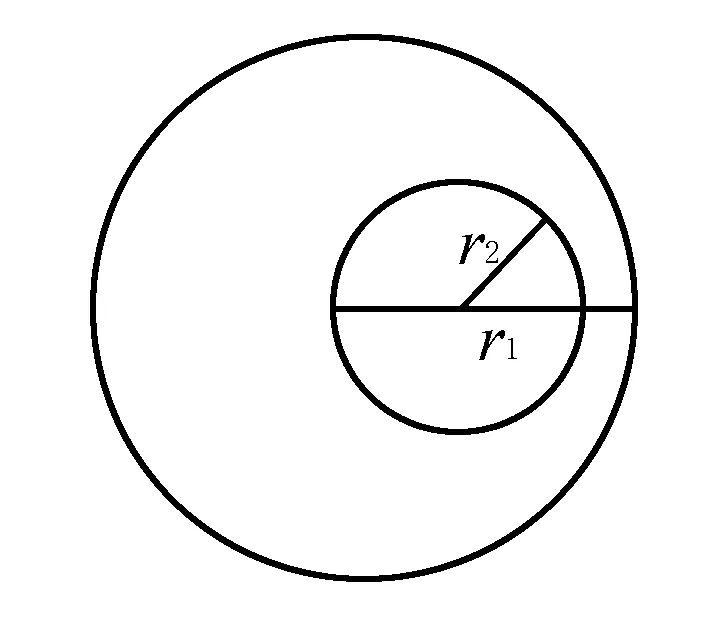
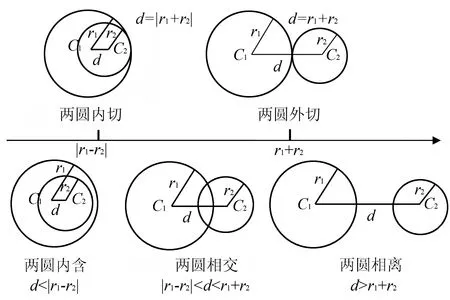
设有圆C1与圆C2,半径分别为r1,r2,两圆的圆心距为d,从下面的图可以看出,平面上两圆的位置关系有五种,可以从两圆的圆心距与两圆的半径大小关系来判断.
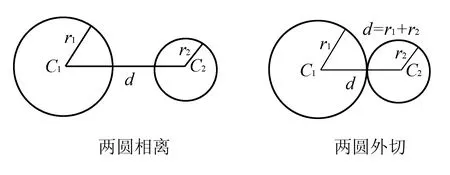
(1)当d>r1+r2时,圆C1与圆C2相离;
(2)当d=r1+r2时,圆C1与圆C2外切;
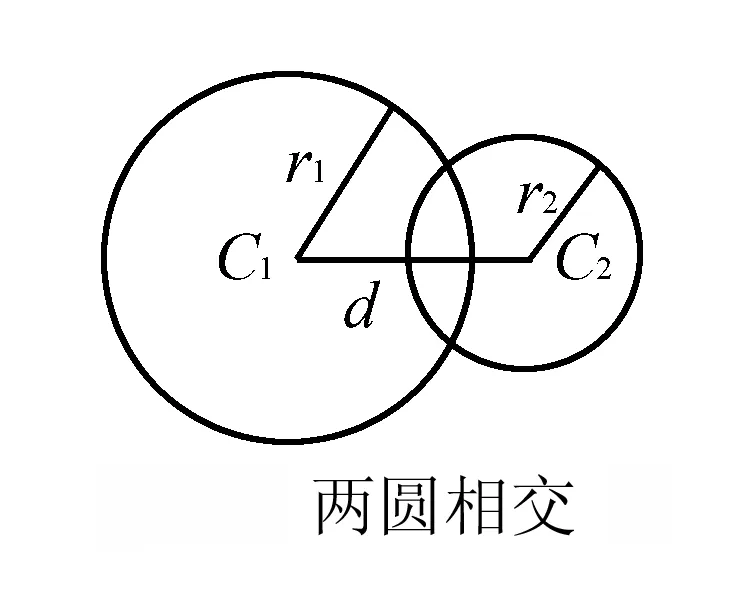
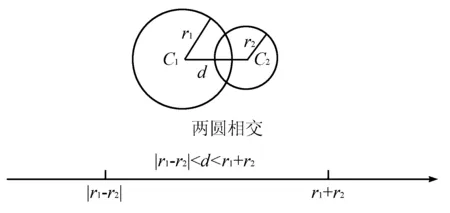
(3)当|r1-r2| (4)当d=|r1-r2|时,圆C1与圆C2内切; (5)当d<|r1-r2|时,圆C1与圆C2内含. 从上面圆与圆的位置我们发现,圆心距d的值与r1+r2,|r1-r2|的值的大小关系决定了圆与圆的位置关系.首先我们画一个数轴,设其为d轴,其上有r1+r2和|r1-r2|.根据圆心距d的大小,两圆的位置关系就可以清晰地在数轴上展现出来(见下图). 今后在解题过程中,我们只需要算出r1+r2,|r1-r2|这两个值,然后将其与圆心距d进行比较,结合数轴,就很容易进行判断了.下面举几个例子进行说明,以显示这种方法的便捷性. 例1 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1和圆C2的位置关系. 解把圆C1的方程化为标准形式为(x+1)2+(y+4)2=25,C1(-1,-4),半径r1=5. 由上图可以看出,圆C1与圆C2相交. (变式):已知两圆C1:x2+y2=1,C2:(x+4)2+(y-a)2=25,若两圆相交,求实数a的取值范围. 解因为圆C1:x2+y2=1,圆心坐标为C1(0,0),半径r1=1. 因为C2:(x+4)2+(y-a)2=25,圆心坐标为C2(-4,a),半径r2=5. 而r1+r2=6,|r1-r2|=4 例2已知圆x2+y2+m=0与圆x2+y2-6x+8y=0没有公共点,求实数m的取值范围. 解因为两圆没有公共点,所以他们之间的关系可以由下面数轴看出. 因为x2+y2-6x+8y=0,即(x-3)2+(y+4)2=25,半径r2=5. 本文通过以上事例展示了在用几何法判断圆与圆的位置关系时,结合数轴,会为我们的解题带来便捷.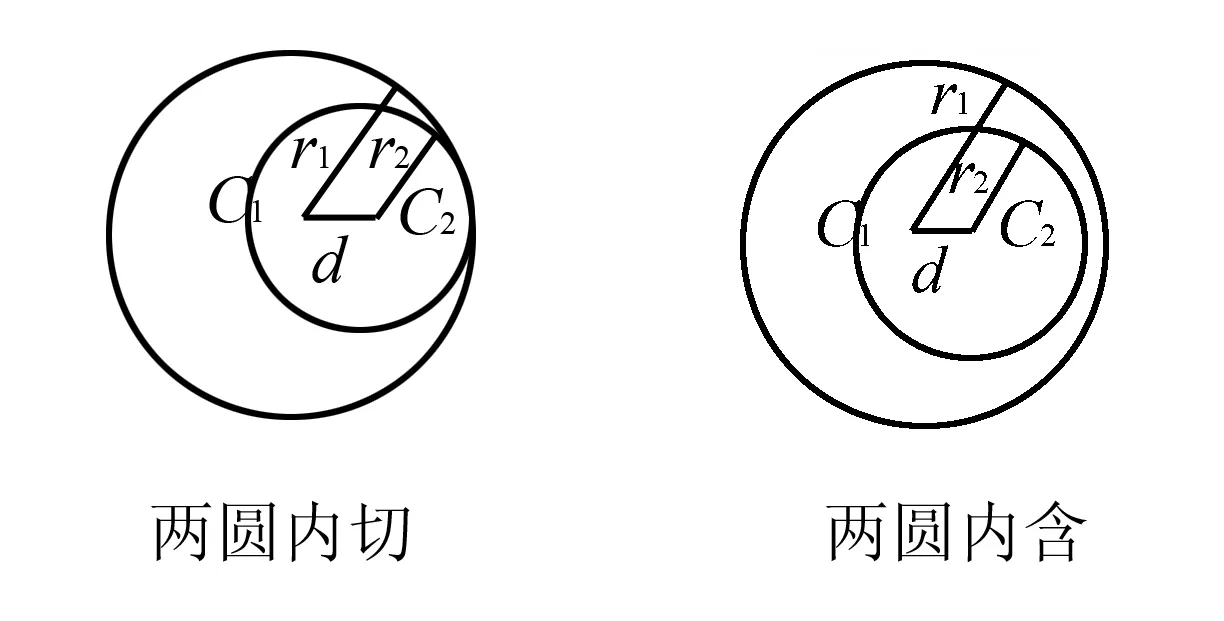
二、结合数轴展示圆与圆的位置关系
三、题型研究