三种不同思路推导动生电动势的表达式

刘 丙

(陕西省西安市鄠邑区第一中学 710300)

在电磁感应现象中，由于引起磁通量变化的原因不同，感应电动势产生的机理也不同.磁场不动，导体运动切割磁感线而引起磁通量变化产生的电动势我们称之为动生电动势.导体棒运动切割磁感线是电磁感应现象的一种特例，本文将分别由法拉第电磁感应定律、动生电动势的产生机理和能量守恒与转化三个角度推导动生电动势的表达式并深入理解，力争有效解决动生电动势相关问题.

一、由法拉第电磁感应定律推导动生电动势

如图1所示，平行金属导轨之间的距离为L，磁感应强度为B的匀强磁场垂直于导轨平面，导体棒以速度v向右匀速运动，在Δt时间内，由实线位置运动到虚线处.在这个过程中磁感应强度B是不变的，闭合回路面积的变化量是阴影部分的面积，即

ΔS=LvΔt

穿过闭合回路的磁通量的变化量是

ΔΦ=BΔS=BLvΔt

根据法拉第电磁感应定律

其中导体棒运动方向v与导体棒ab垂直，也与磁感应强度B垂直.

1.若导体棒运动方向v与导体棒ab本身不垂直，但与磁感应强度B垂直，如图2所示.

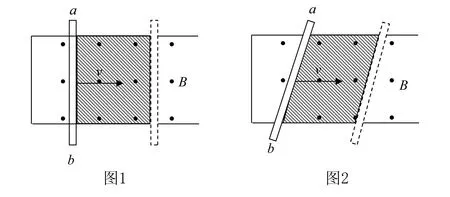
在Δt时间内，导体棒ab由实线位置运动到虚线处.在这个过程中闭合回路面积的变化量是阴影部分的面积

ΔS=LvΔt

穿过闭合回路的磁通量的变化量是

ΔΦ=BΔS=BLvΔt

根据法拉第电磁感应定律

可见，若导体棒ab运动方向v与导体棒ab本身不垂直，此时L指的是导体棒在垂直于速度v方向上的投影的有效长度.

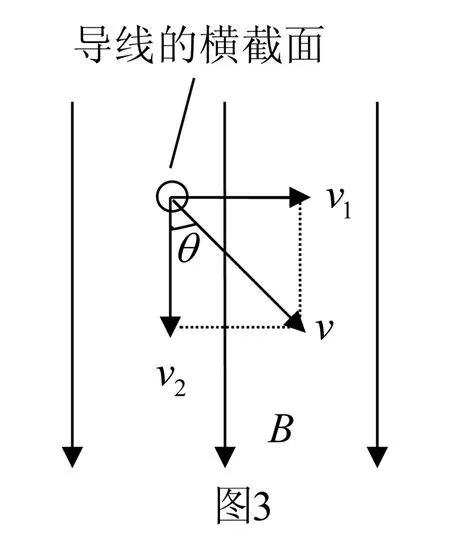
2.若导体棒ab运动方向v与导线本身垂直，但与磁感应强度B有一个夹角θ，则可将导体棒速度v沿平行于磁场方向和垂直于磁场向分解，如图3所示.

速度v在垂直于磁场向分v1=vsinθ

速度v在平行于磁场向分v2=vcosθ

其中v2平行于磁场向，导体棒ab不切割磁感线，v2方向不产生感应电动势；

v1方向切割磁感线产生的感应电动势为

E=BLv1=BLvsinθ

可见，若导体棒运动方向与导线本身垂直，但与磁场方向有一个夹角θ，则可将速度v分解为沿磁场方向和垂直于磁场方向；亦可将磁感应强度B分解为沿速度方向和垂直于速度方向来处理相关问题.

3.对于导体棒运动切割磁感线运动感应电动势E=BLvsinθ，如果v是某一时刻的瞬时速度，则E是该时刻的瞬时感应电动势；如果v是某一段时间的平均速度，则E是该段时间内的平均感应电动势.

二、由动生电动势产生机理推导动生电动势

导体在磁场中做切割磁感线运动产生动生电动势的本质是由于导体中的自由电荷受到洛伦兹力而引起的.

如图4所示，长度为L导体棒AC在匀强磁场中以速度v向右运动切割磁感线，其中导体棒AC与磁场方向和运动方向均垂直.由于金属导体中有自由电子，所以导体棒中的自由电子随导体棒一起以速度v向右运动.每个自由电子受到的洛伦兹力为f=evB，洛伦兹力f的方向沿导体棒向上.在洛伦兹力f的作用下，自由电子向上运动会积累到导体棒的A端，因而C端出现了净剩的正电荷.AC两端出现了沿导体棒向上的静电场E电，此电场对自由电子的静电力沿导体棒向下，如图5所示.

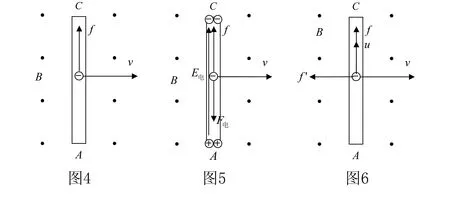
随着AC端电荷的积累，静电场电场强度E电逐渐增大，当洛伦兹力f与静电力F电平衡时，AC两端便形成了一个稳定的电势差UAC.此时导体棒相当于一个电源，UAC是电源处于开路时，电源的端电压，即UAC是此电源的电动势.当洛伦兹力f与静电力F电平衡时

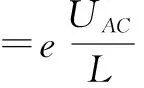
故动生电动势E=UAC=BLv

需要说明的是，这种情况下洛伦兹力仍然是不做功的.因为当导体棒向右运动，自由电子受沿导体棒向上的洛伦兹力f会沿导体棒以速度u向上运动.正是由于自由电子以速度u向上运动才会产生感应电流.由于自由电子以速度u向上运动，自由电子还会受到向左的洛伦兹力f′，如图6所示.

在很短一段时间Δt内，向上的洛伦兹力f对自由电子做功为：

W1=f(uΔt)=evB(uΔt)

向左的洛伦兹力f′对自由电子做功为：

W2=-f′(vΔt)=-euB(vΔt)

洛伦兹做的总功W=W1+W2=0

由此可以看出，洛伦兹力仍然是不做功，洛伦兹力只是一个“搬运工”，起传递能量的作用.即外力克服f′所做的功，通过f转化为感应电流的能量.

三、由能量守恒与转化角度推导动生电动势

如图7所示，平行金属导轨之间的距离为L，磁感应强度为B的匀强磁场垂直于导轨平面，导体棒ab以速度v向右匀速运动，不计其他电阻.

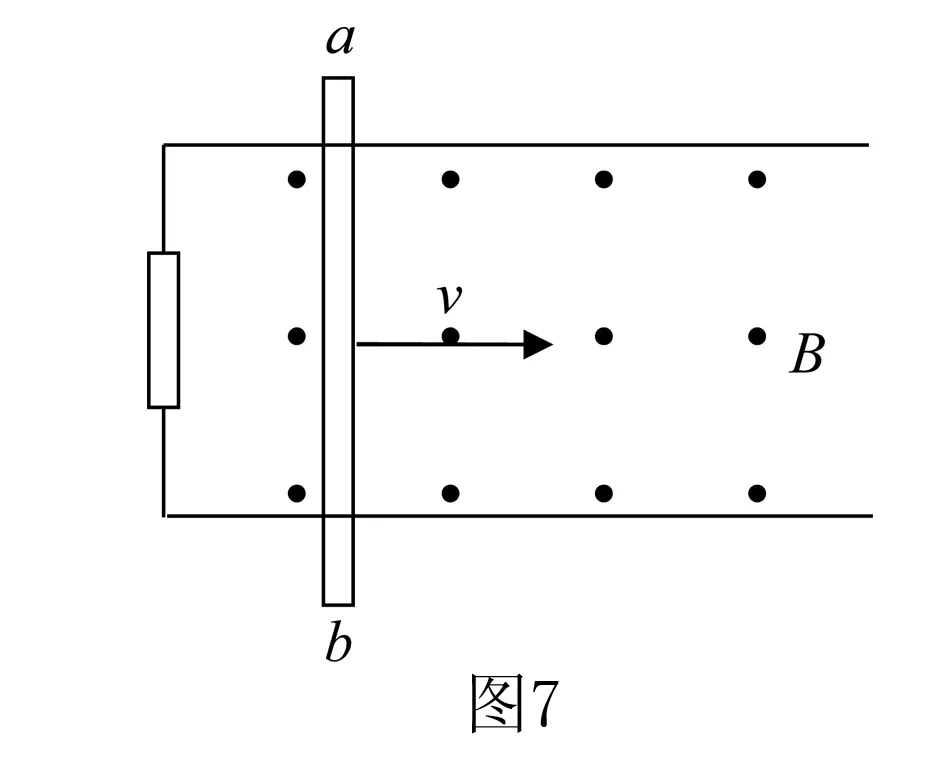
设由于导体棒向右匀速运动，闭合回路的感应电动势为E，感应电流为I.

以导体棒为研究对象有，F外=F安

F安=BIL

外力F外做功的功率P=F外v=BILv

闭合电路中的电功率P电=EI

根据能量的转化及守恒定律知P=P电即

E=BLv

由此可以看出，发生电磁感应时往往伴随着其他物理现象的发生.当闭合回路磁通量发生变化时产生了感应电动势，而回路中感应电流的大小可以由闭合回路的欧姆定律得到.通电导线在磁场中又要受到安培力，这样就可以把电磁感应问题、电路问题和力学问题联系起来.但总体来看从能量转化与守恒角度推导动生电动势更有利于提高学生对综合问题的分析能力.