例谈立体几何中证明位置关系的转化关系

杜红全

(甘肃省康县教育局教研室 746500)

把空间图形的问题转化为平面图形的问题，然后用平面几何的知识去解决，这是立体几何的永恒的主题.立体几何中有两个特殊的位置关系，即线线、线面、面面的平行与垂直，平行与垂直也是高考的热点.在判断或证明位置关系时关键要理解线线、线面、面面的平行与垂直的内在联系，平行与垂直的判定和性质无一不蕴含了转化思想，下面让我们走进空间中的平行与垂直关系一起去感受一下吧.

一、平行关系的转化

空间中线线、线面、面面平行关系的转化为：

因此，在证明平行有关问题时，应抓住“转化”这种思想方法来达到论证的目的.

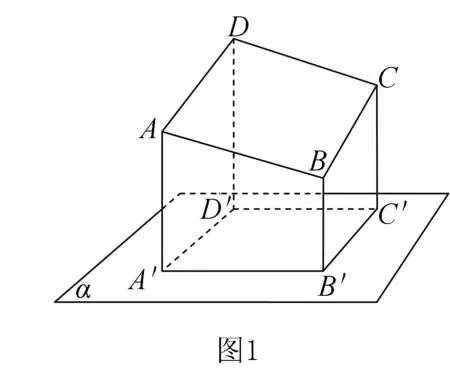
例1如图1，平面四边形ABCD的四个顶点A、B、C、D均在平行四边形A′B′C′D′所确定一个平面α外，且AA′、BB′、CC′、DD′互相平行.

求证：四边形ABCD是平行四边形.

分析充分利用A′B′C′D′的平行关系及AA′、BB′、CC′、DD′间的平行关系，证明出AD∥BC与AB∥CD即可.

证明因为四边形A′B′C′D′是平行四边形，所以A′D′∥B′C′.又因A′D′⊄平面BB′C′C，B′C′⊂平面BB′C′C，所以A′D′∥平面BB′C′C.同理AA′∥平面BB′C′C.又因为A′D′⊂平面AA′D′D，AA′⊂平面AA′D′D，A′D′∩AA′=A′，所以平面AA′D′D∥平面BB′C′C.又因为平面ABCD∩平面AA′D′D=AD，平面ABCD∩平面BB′C′C=BC，所以AD∥BC.同理可证AB∥CD.所以四边形ABCD是平行四边形.

点评本题证明过程体现的是线线平行、线面平行、面面平行之间的互相转化，即由A′D′∥B′C′得到A′D′∥平面BB′C′C，实现了由线线平行向线面平行的转化，应用了线面平行的判定定理；由A′D′∥平面BB′C′C与AA′∥平面BB′C′C得到平面AA′D′D∥平面BB′C′C，实现了由线面平行向面面平行的转化，应用了面面平行的判定定理；由平面AA′D′D∥平面BB′C′C得到AD∥BC，实现了由面面平行向线线平行的转化，应用了面面平行的性质定理.

二、垂直关系的转化

空间中线线、线面、面面垂直关系的转化为：

因此，在证明垂直有关问题时，应抓住“转化”这种思想方法，每一种垂直的判定都是从某一垂直开始转向另一垂直，最终到达目的.

例2 已知，如图2，平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E为垂足.

(1)求证：PA⊥BC；

(2)当E为△PBC的垂心时，求证：△ABC是直角三角形.

分析(1)需证PA⊥平面ABC，即证PA与平面ABC内的两条相交直线垂直，可由面面垂直来构造直线；(2)只需证AB⊥AC，即证AB⊥平面PAC.

证明 (1)如图2，在平面ABC内任取一点D，作DF⊥AC于点F，作DG⊥AB于点G.因为平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，所以DF⊥平面PAC.又因为PA⊂平面PAC，所以DF⊥PA.同理可证DG⊥PA.又因为DG∩DF=D，DG⊂平面ABC，DF⊂平面ABC，所以PA⊥平面ABC.又因为BC⊂平面ABC，所以PA⊥BC.

(2)如图2，连接BE并延长交PC于点H.因为E为△PBC的垂心，所以PC⊥BH.又因为AE⊥平面PBC，PC⊂平面PBC，所以PC⊥AE.又因为BH∩AE=E，BH⊂平面ABE，AE⊂平面ABE，所以PC⊥平面ABE.又因为AB⊂平面ABE，所以PC⊥AB.由(1)知PA⊥平面ABC，又因为AB⊂平面ABC，所以PA⊥AB.又因为PA∩PC=P，PA⊂平面PAC，PC⊂平面PAC，所以AB⊥平面PAC.又因为AC⊂平面PAC，所以AB⊥AC，即△ABC是直角三角形.

点评本题是一道线线、线面、面面垂直关系的综合应用，体现了垂直转化，求解本题的关键是用好垂直关系.

三、平行与垂直关系的转化

空间中线线、线面、面面平行与垂直关系的转化为：

因此，在证明平行与垂直有关问题时，应抓住“转化”这种思想方法，最终达到解题的目的. (1)由线线平行得到线面垂直的判定方法:如果两条平行线中一条垂直于一个平面，那么另一条也垂直于这个平面；(2)由线面垂直得到线线平行的判定方法:垂直于同一平面的两条直线平行；(3)由线面垂直得到面面平行的判定方法：垂直于同一直线的两个平面平行；(4)由面面平行得到线面垂直的判定方法：如果两个平行平面中一个直于一条直线，那么另一个平面也垂直于这条直线.而线线与面面平行在前面已举例说明，在此不在赘述.

例3如图3，在正方体ABCD-A1B1C1D1中，EF为异面直线A1D与AC的公垂线，求证：EF∥BD1.

分析利用垂直于同一平面的两条直线平行，只需证EF⊥平面A1C1D与BD1⊥平面A1C1D即可.

证明如图3，连接A1C1，则四边形A1ACC1是平行四边形，所以AC∥A1C1.又因为EF⊥AC，所以EF⊥A1C1.又因为EF⊥A1D，A1D∩A1C1=A1，所以EF⊥平面A1C1D.

连接B1D1.因为BB1⊥平面A1B1C1D1，A1C1⊂平面A1B1C1D1，所以BB1⊥A1C1. 因为四边形A1B1C1D1是正方形，所以B1D1⊥A1C1.又因为B1D1∩BB1=B1，所以A1C1⊥平面BB1D1D.又因为BD1⊂平面BB1D1D，所以A1C1⊥BD1.同理可证BD1⊥DC1.又因为A1C1∩DC1=C1，所以BD1⊥平面A1C1D.所以EF∥BD1.

点评本题是由线面垂直⟹线线平行，证明本题的关键是EF⊥平面A1C1D与BD1⊥平面A1C1D.由于EF为异面直线A1D与AC的公垂线，这一条件构造线面垂直十分有用.

例4 如图4，在正方体ABCD-A1B1C1D1中，M,N,P分别是C1C,B1C1,C1D1的中点，求证：平面PMN∥平面A1BD.

分析利用垂直于同一直线的两个平面平行，只需A1C⊥平面PMN，A1C⊥平面A1BD即可.

证明如图4，连接AC1,AC.因为ABCD-A1B1C1D1是正方体，所以四边形ABCD是正方形.又因为AC和BD是正方形ABCD的对角线，所以AC⊥BD.又因为CC1⊥平面ABCD，BD⊂平面ABCD，所以CC1⊥BD.又因为AC⊂平面ACC1，CC1⊂平面ACC1，AC∩CC1=C，所以BD⊥平面ACC1.又因为AC1⊂平面ACC1，所以AC1⊥BD.同理可证AC1⊥A1B，又因为BD⊂平面A1BD，A1B⊂平面A1BD，BD∩A1B=B，所以AC1⊥平面A1BD.同理可证AC1⊥平面PMN，所以平面PMN∥平面A1BD.

点评本题是由线面垂直⟹面面平行；此题还可以利用平面与平面平行的判定定理来证明，关键是MN∥平面A1BD与PN∥平面A1BD.即用线线平行⟹线面平行⟹面面平行.