面向任务的物资供应路径优化决策建模研究
2020-06-05艾云平
艾云平
(安徽外国语学院 国际商务学院,合肥 231201)
面向任务的物资的物流,应视有利的前送时机,把客户需求的物资及时、准确地运送到位,这要求指挥决策人员合理组织运输力量、科学选择运输路线,满足客户的物资需求时间要求,以达到最大效益。一般来说,运输路线的不合理因素主要包括同种物资在同一段运输路线上“相对运送”或“迂回运输”等这种不符合节约里程的运输,不仅增加了物资的物流费用,还浪费了运力,也降低了物资流转速度。科学合理的运输,不仅要求物资物流的吨公里最低,而且要求去掉不必要的装卸工作量。研究各种物资物流问题的相关文献很多,需要根据物资的供应保障运输问题特点进行选择。目前,理论研究的热点是物流最短路径,即节约里程问题,也就是从运输起点到运输终点的里程最短的问题,但该问题涉及大规模的路网节点,而运输起点到运输终点不存在有很多路网节点的情况,且小范围内的运输路线一般都是确定的,故研究面向任务的物资供应物流路径优化决策问题具有重要的理论意义和现实意义。本文采用运筹学方法,建立面向任务的物资供应路径问题的优化模型,并设计智能求解算法对模型进行求解。
1 面向任务的物资供应物流路径问题分析
面向任务的物资供应路径优化问题可简单理解为:只有一个被选物资仓库,已知物流任务,车辆从物资仓库出发,如何选择物流路径,在服务若干个物资需求客户后回到物资仓库。问题输出是确定所需的运输车辆数以及每辆车的运输路线。车辆作为运输保障的主要运输工具,物资供应路径的优化决策需要达到最大的经济效益,即以一定的优化目标,确定所需的运力(车辆数)和每辆车的运输路线,满足运输任务要求。
本研究可详细表述为:已知需要运送给各需求客户的物资数量,物资仓库可组织若干辆同类型的运输车辆来完成此次运输任务,每辆车都有容量限制,所载物资总量不得超过其容量。开始时刻所有车辆都停放在仓库中,有需求用户在空间内任意分布,需要确定所需的车辆数和每辆车的行驶路线,使车辆有序地把物资运送到各需求客户,最后所有车辆返回物资仓库。需要满足的假设如下:
(1)所有运输车辆以物资仓库为起点并最终返回物资仓库;
(2)每个需求客户只被一辆车访问一次且每辆车只能服务一条路线;
(3)在每条运输路径上,运送给各需求客户的物资数量之和不能超过车辆的载重数量。
一般来说,客户对物资的运输到达时间有一定限制,故车辆路径问题具有时间约束,这就要求运输过程中必须考虑先满足急需,再满足一般需求。为了深入研究,这里引入带时间窗的车辆物流路径问题(VRPTW)。
VRPTW问题是在传统的车辆物流路径问题的基础上增加时间窗这一约束条件,时间窗约束一般情况下可分为三种,即混合时间窗、硬时间窗和软时间窗[1]。VRPTW问题需要根据路径查找、装载量限制、物资需求客户的服务次序这三项关键问题进行决策。带时间窗的车辆路径问题,由于首要任务就是各个需求客户对时间要求的问题,所以对客户服务次序的确定是带时间窗的车辆物流路径问题中关键问题。
在物资运输过程中,各个物资需求客户对物资运达时间的要求很高,如果不能在规定的时间内把物资送达客户,将直接影响客户的经济效益,因而本文研究带硬时间窗的车辆路径优化问题。
在优化目标的选择上,运输时间和运输距离是必须优先考虑的决策因素。由于各需求客户的硬时间窗要求将在建模时予以考虑,从运输距离的角度来看,运输时间、运输保管及损毁、运输成本等因素都与其有一定的比例关系,所以优化运输路径、节约运输里程无论是从微观还是从宏观角度,都有利于提高物资的物流效益。因此,以总的运输距离最短作为优化目标,在满足军事效益的同时,对经济效益也有兼顾,有利于提高物资的综合运输效益。
2 面向任务的物资供应路径优化问题建模
2.1 参数定义
假设现有一运输任务,要求运送给需求客户i的物资数为qi,需求客户i有一个时间窗口[0,bi],这个时间窗口表示车辆必须在时间bi之前到达需求客户i。设需求客户集合为C,需要的运输车辆数集合为V,每辆运输车的装载容量为Q,且qi 对于每条弧(i,j)(ij,in+1,j0)和车辆k定义变量xijk: 则需设计一条所有车辆的总运输距离最小的路径,此路径开始于顶点0,终止于顶点n+1。同时,还要保证计划供应给每个需求客户的物资得到满足,且不能违背各需求客户的硬时间窗口和车辆的运能约束。经上述参数描述,该VRPTW 的数学模型就可以表示为: (式1) (式2) (式3) Rk={rki|rki∈{1,2,…,n},i=1,2,…,nk} (式4) (式5) (式6) (式7) tik≤bi,∀k∈V,∀i∈N (式8) xijk∈{0,1},∀k∈V,∀i,j∈N (式9) q,bi,dij,qij,tij∈Z+,∀i,j∈N (式10) 式1表示运输目标为所有车辆行驶的总距离最短; 式2表示每条路径服务的需求客户数量不超过需求客户总数; 式3表示运输给每条路径上的各需求客户物资总量不超过车辆的容量限制; 式4表示第k辆车的路径组成; 式5、式6和式7表示每辆车始于物资仓库,访问需求客户后回到物资仓库; 式8表示车辆行驶过的时间窗约束; 式9和式10为取值约束。 带硬时间窗的车辆路径问题已被证实是NP难问题。目前,关于解决此类问题的算法已经很多,对于大型的车辆路径问题,常用的有禁忌搜索算法、遗传算法等。本文基于常用的传统算法,设计了基于蚁群算法的模型算法,该模型算法的主要优点在于针对大型车辆的路径问题具有一定的实用性。 m表示蚁群中蚂蚁的数量; a表示信息因子,即信息素的重要程度; b表示期望因子,即能见度的重要程度; r表示信息在时间间隔(t,t+n)内衰减的比例,其中0 tij表示e(vi,vj) 上信息素的强度; hij表示e(vi,vj)的能见程度,通常情况下取hij= 1/Disij; Dtij表示蚂蚁k在e(vi,vj)上单位长度的信息增量; Disij表示节点vi与vj连接所成边的的距离,vi,vjV。 在蚁群系统中,蚂蚁具有下面几个特征: (1)概率决定转移路线。依据节点之间距离和路径上信息量的函数,即用概率来决定转移路线。 (2)信息素积累原则。每完成一次循环后,路径上留的信息素逐渐递增。 (3)信息素时间衰减规律。蚂蚁留在路径上的信息素量随时间逐渐挥发,增量逐渐衰减。 蚁群算法求解的一般流程如图1所示。 首先,各个路径上的信息素量相等,且蚂蚁可随机选择转移路径,并留下一定量的信息素;其次,蚂蚁根据信息素的分布和可行路径的能见度进行路径转移决策;最后,依据路径信息素强度的不断积累情况寻求最优或近似最优路径。 (1) 初始化。设置各个参数的初始值,即:信息素tij(0) =c(c为常数);信息素增量Dt(0) =c;能见度权重因数hij,且一般取hij= 1/Disij。 (2) 释放蚁群。随机给定起始节点,并记录蚂蚁的起始点,用来作为后续判断蚂蚁是否搜索完所有路径的标志。 (3) 依据概率选择移动方向。节点vi上的蚂蚁选择下一节点vj的概率由信息素浓度tij和能见度因数hij共同确定,其寻优过程依据概率进行,其转移概率的表达形式为: (式11) 其中,allowedk= {V-tabuk}表示蚂蚁k在有联通路径的点中下一步可以选择的节点;tabuk表示第k只蚂蚁已经走过的路径集合;V为蚂蚁可以选择的目标节点集合; a 、b 两参数反映信息素强度与能见度信息的相对重要性,其值一般通过实验的方法来确定。 (4) 更新信息素。一次循环完成后,所得路径上的信息素量根据下式进行调整,表达式为: τij(t+1)=Δτij(t,t+1)+(1-ρ)τij(t) (式12) (式13) 3.3.1 可行点集allowedk的动态调整 在VRPTW问题中,由于每只蚂蚁需要遍历所有路网节点,且每只蚂蚁的移动次数是不确定的,因此,在求解VRPTW问题的每次迭代过程中,只能将是否已经回到出发的原点(仓库)作为路径构造完成的标志,即包括两个相同的原点(仓库)节点。在基于蚁群算法求解VRPTW问题中,本文将路径构造过程分为以下两个阶段: (1)如果蚂蚁的初始节点位置不是物资仓库时,第一个阶段就是由初始节点出发寻找物资仓库的过程,称为“过程Ⅰ”。在寻找中,可行点集allowedk中一定要包括物资仓库,而不能包括初始节点。在到达物资仓库后,接下来就是从物资仓库出发找寻一条返回初始节点的路径,该过程称为“过程Ⅱ”。在此过程中,allowedk中通常应包含初始节点等相关信息,但不能包含物资仓库等相关信息。 (2)如果蚂蚁的初始位置节点是物资仓库,“过程Ⅰ”就是蚂蚁的首步移动,即由物资仓库移动到任意其他节点的过程。“过程Ⅱ”就是蚂蚁回到物资仓库的过程。因此,在“过程Ⅱ”中,allowedk必须包含物资仓库,而在“过程Ⅰ”中,allowedk又不能包含物资仓库。 可见,为满足路径搜索的需要,可行点集allowedk需要不断地进行动态调整。 3.3.2 选择概率优化 蚂蚁在选择下一个物资需求客户时,应考虑满足两个基本前提,即时间窗和车辆容量约束。除此之外,还必须考虑时间窗和路径的择优这两个因素。 (1)时间窗优选问题。时间窗因素优选的原则为:等待时间较短优先和时间窗较小优先。由于受下一个物资需求客户j的时间窗和当前节点到需求客户j的时间等因素影响,在当前节点i,将第k条路径上的蚂蚁物流路径的转移概率进行改进,即选择下一物资需求客户j的概率计算公式改进为: (式14) 其中,a和b为权重系数, (2)路径择优问题。主要考虑通往下一个物资需求客户的路径信息量和路径长度。 3.3.3 参数优化 将信息素的取值限制在区间[tmin,tmax],其目的就是为最大限度地减少陷入搜索停滞,同时确保某条路径上的信息素浓度极端化问题,即远大于其他路径,进而导致算法瘫痪或进入死循环。 在蚁群算法的初始路径寻优阶段,较大的r值具有优先级别功能。在一定的范围内,随着r的不断增大,算法的整体性越来越好[2]。因此,在路径优选过程中,应尽量选用较好的r值进行,否则通常按照下式进行调整。 (式15) 基于改进的蚁群算法,设计了对带硬时间窗的车辆路径问题求解的基本流程。即:用人工蚂蚁代替车辆来服务物资需求客户,当被选客户物资需求运载总量超出汽车现有的物资数量时,则返回至物资仓库,表示此次运输已完成,否则一直到完成一次服务为止。此时,代表车辆的人工蚂蚁就完成了一次巡游,当全部蚂蚁都完成后,记作一次循环。则所需的车辆数就是此次循环中那只所走总路径最短的蚂蚁往返于物资仓库的次数。每一次循环结束之后,每只蚂蚁巡游线路的优选分析,必须根据信息素的增量及其发展变化进行。经过多次循环后,如果大部分蚂蚁物流路径的选择相同或优化完毕,则求解完成。求解具体步骤如下: Step 1:参数原始初始化,取t= 0,置迭代次数NC_max = 0,读取路网信息,将m只蚂蚁放置于代表物资仓库的节点,建立蚁群禁忌表tabuk和可行点集allowedk。 Step 2:从节点列表中搜索遗漏节点,针对每只蚂蚁i而言,按照概率转移公式(式14)计算转移概率,再按照转移概率利用轮盘赌法[3]选择蚂蚁下一个服务的需求客户j。 Step 3:考虑路径(i,j)的目标需求客户j的物资供应量后,总的供应量为q,如果q Step 4:求解需求客户j的到达时间,如果到达时间满足时间窗的要求,则把相应节点j加入tabuk禁忌表中,跳转到Step 2,否则将节点j重新加入可行点集allowedk中,跳转到Step 5[5]。 Step 5:蚂蚁返回物资仓库,对车辆数加1(初始为0),然后对可行点集allowedk进行判断。如果allowedk为空,那么跳转到Step 6,否则从allowedk中获得未搜索过的节点,并以此作为起点,跳转到Step 2,搜索下一个节点[6]。 Step 6:在每次完成一次巡游之后,就需要对蚂蚁所走过的路径按照信息素更新公式(式12和式13)进行信息素更新,并记录巡游路径总长度。 Step 7:当m只蚂蚁完成搜索后,搜索得到本次迭代中的车辆最短路径长度和所需的车辆数。将全局最优解与本次迭代的最优解进行对比,并选择最优解,尔后根据需要按Step 6的步骤更新信息素。 Step 8:对最大迭代次数和全局最优解进行博弈,即只要两者达到一个,则程序结束,输出相关结论为最优路径解和所需的车辆数,否则跳转到Step 2,重复上述步骤。 需要说明的是,如果仅根据信息素的浓度大小来搜索选择下一服务节点,智能算法很容易较早地收敛于一条路径,导致不能再去搜索空间中更短的路径,即出现停滞现象。同时,为了避免过早收敛,在Step 2中使用了轮盘赌法选择下一个节点。 主要研究面向任务的物资供应的路径优化决策问题,其成果可直接用于紧急情况下乃至战时物资的车辆路径优化决策。考虑各个客户物资需求的硬时间窗要求,以所有车辆运输总距离最短作为优化目标,创建了数学优化模型。从规模上来说,文中研究的路径决策问题属于小型问题的范畴,模型的解用精确解法就可以得出。但是,为了进一步扩展文中所建模型的适用范围,根据所建模型特点,设计了基于改进的蚁群算法,优化结果为输出车辆数、每辆车的运输路径和运输总距离。2.2 数学模型构建
3 基本蚁群算法的物资供应路径优化模型求解
3.1 参数设定
3.2 算法求解流程
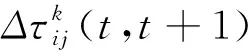
3.3 求解算法的改进
4 求解过程的算法设计
5 结论
