关于极大外平面图的度偏差的极值
2020-06-03
(湖南师范大学 数学与统计学院,长沙,410081)
1 引言
本文仅考虑简单、无向、连通和有限的图G,分别有边集E(G)和顶点集V(G).以G-{vi}(1≤i≤n)表示从G中去掉顶点vi后得到的子图,dG(vi)表示G中vi的度(可简写为d(vi)),nj(1≤j≤n-1)表示图G中度为j的顶点个数,N(v)表示顶点v的邻点集,Pn表示有n个顶点的路,G1和G2的联图G1∨G2表示G1和G2中各顶点互相连接后所得到的图,符号[a]表示对a取小于等于a的最大整数.在文献[1]中提到,若平面图G的所有点都在外部区域上,则称此平面图G是外平面图;若外平面图G不能再加上边而不失去外平面性,则称此外平面图G为极大外平面图.我们把外部区域的边界称为界环.显然界环是一个圈,用Cn=(v1,v2,…,vn)来表示,圈Cn上的点下标连续且v1与vn相邻.易见,极大外平面图有2n-3条边(n≥3).没有提到的定义、术语请参见文献[1].

2 预备知识

图
当n=3,4,5时,只有一个非同构的极大外平面图,当n=6时,有三个非同构的极大外平面图, 具体见图2.
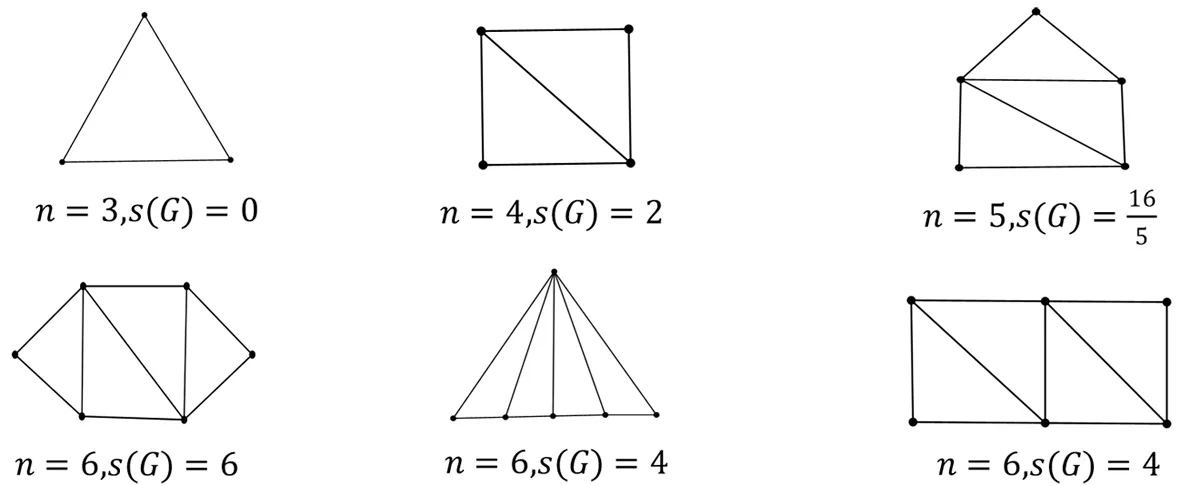
图2 n≤6的极大外平面图
下面先介绍极大外平面图的有关性质.
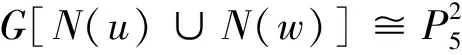
引理2[1]设G是有n个顶点的外平面图(n≥3),那么G为极大外平面图的充要条件是在G的边界Cn内的所有区域均为三角形.

引理4[10]设G是有n个顶点的极大外平面图(n>3),则G的任意两个二度顶点不能相邻.当n=3时,极大外平面图是一个三角形,此时三个顶点彼此相邻且度为2.
由极大外平面图的定义我们易得下面结论.
引理5设G是有n个顶点的极大外平面图(n≥3),则图G界环上的每条边只能存在于一个三角形中.
引理6设G是有n个顶点的极大外平面图(n≥3),且n2=2,则有n3≥2.
证明由极大外平面图的定义,由G的边界上四个下标连续的顶点导出的子图只有图3中的a,b,c三种情况.下面对该三种情况分别进行讨论.

图3 极大外平面图G的边界的四个下标连续的顶点的3种导出子图
(i)当G中存在边界的四个下标连续的顶点的导出子图a时,设v1左边边界上的邻点为vn,由引理2可知,v3必与除v1,v2,v4的顶点外至少还有一个邻点:
若v3与vn不相邻,则v3必与vx∈VG{v1,v2,v3,v4,vn}相邻.故可把G分为①,②,③三个部分,如图4所示.显然,这三个部分都是极大外平面图.由引理4可知,在①中必有一个除v1,v3,vx外的2度顶点(因为v3与vn不相邻,所以v1在①中不是2度顶点),在③中必有一个除v3,vx外的2度顶点.又d(v2)=2,所以在G中就至少存在三个二度顶点,这样就与G中n2=2矛盾了.
若v3与vn相邻,则vn,v1,v2,v3的导出子图为情况b,此时d(v2)=2,d(v1)=3.再考虑v4的度的情况.当v3与v5相邻时,如图5所示,d(v4)=2.令G′=G-{v2,v4},则G′也是极大外平面图.在G′中,因为v3与vn相连,所以dG′(v1)=2.再根据引理4,若在G′中v5不是2度顶点,则除v1,v3,v5外G′至少还有一个2度顶点,故G中至少有三个二度顶点,与n2=2矛盾.所以v1,v5必是G′中的2度顶点,此时v3与vn,v3与v6相邻,d(v1)=d(v5)=3.当v3与v5不相邻时,d(v4)≥3.综上所述,当只有一个顶点的度为2时,至少伴随一个3度顶点;当有两个顶点的度为2时,至少伴随两个3度顶点.

(ii)当G中存在边界的四个下标连续的顶点的导出子图b时,根据引理2,必有d(v2)=2,d(v3)=3,d(v4)≥3,所以一个2度顶点必定至少伴随一个3度顶点.
(iii)当G中存在边界四个下标连续的顶点的导出子图c时,由极大外平面图定义可知,d(v2)≥3,d(v3)≥3.接下来考虑v1,v4的度.当d(v1)=2,即v2与vn相邻时,若v3与vn相邻,则vn,v1,v2,v3的导出子图为图3中情况b;若v3与vn不相邻,则vn,v1,v2,v3的导出子图为图3中情况a.同理,当d(v4)=2时,有同样的结果.故存在一个2度顶点必定伴随一个3度顶点.
综上分析,当n2=2时,n3≥2得证.

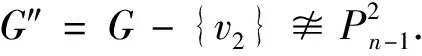
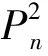
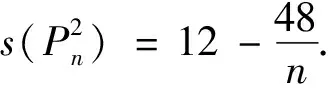
3 主要结论
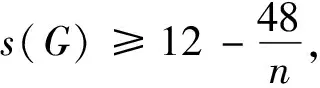
证明显然当n=7时,有4个不同构的极大外平面图(如图6).

图6 4个不同构的7阶极大外平面图
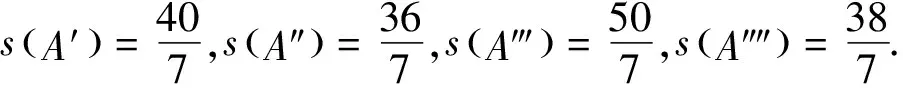
近年来,通过与北京、上海、山东、吉林、湖北、湖南、广西、贵州、内蒙古等省、自治区、直辖市的数十个区县党委统战部门的交流,结合重庆基层统战工作的现状,发现尽管基层统战工作在某些方面存在的问题有重庆的个性,但就其他方面的问题来说,全国各地不同程度地存在同样的问题。新时代基层统战工作创新发展的制约因素主要包括如下:

令
由引理1知,d(u)+d(w)≥7,故有下面的结论:

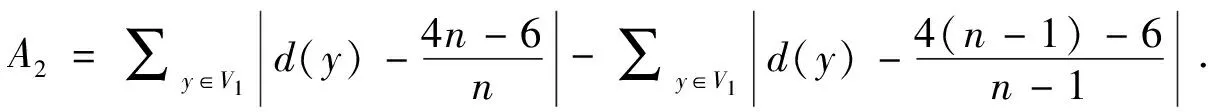
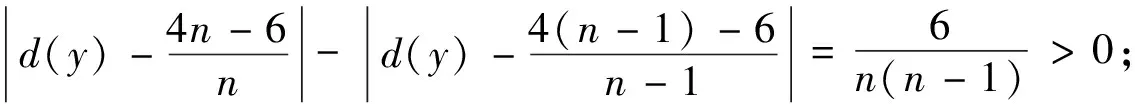
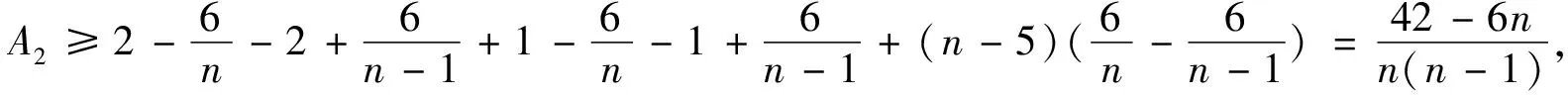
定理2若G是一个n≥6的极大外平面图,则
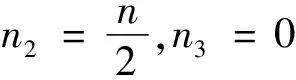

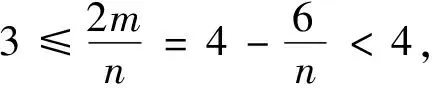
所以s(G)的值只与n2,n3有关.
又因为G中必定存在2度顶点,所以我们首先确定一个2度顶点v2,再分析v3,v4的度的大小.