An Improved Straight Walk Algorithm for Point Location in a Tetrahedral Mesh
2020-06-03LiJiaoHuangFenGuoRongYingJinyong
Li Jiao Huang Fen Guo Rong Ying Jinyong
(1.School of Mathematics and Statistics, Changsha University of Science and Technology, Changsha, Hunan 410114, China;2.School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China)
Abstract The straight walk algorithm is commonly-used in searching for a mesh cell containing a query point in a given large scale unstructured mesh of a bounded domain.It could be used in computational geometry and several other fields, including solving partial differential equations with the finite element method.However, this algorithm does not work in some degenerate cases, such as the intersection point coincides with the vertex.In this paper, as an improvement, a new straight walk algorithm is presented to make it work for degenerate(or singular)cases in a tetrahedral mesh, which is well verified in our numerical tests.
Key words Straight walk algorithm Tetrahedral mesh Degenerate case Point location
1 Introduction
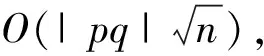
In our recent work, in order to validate the new program packages and verify our proposed algorithms for solving the elliptic interface problems by the finite element method[7,8,9,10], the straight walk algorithm is commonly used to construct the nested meshes so that the convergence order can be fully used.From various numerical tests, we observed that the straight walk algorithm failed to work in some degenerate cases including the one when the line segmentpqfrom the start pointpto the query pointqoverlaps an edge of a mesh cell(See Fig 1).Although there exist some other algorithms which could handle this degenerate cases well, we still want to do a little improvement about the straight walk algorithm.This motivated us to improve the current straight walk algorithm.
Some degenerate cases of 2D triangulation meshes were treated successively in[11]through using the implicit line equation test and the Remembering Stochastic walk algorithm.Due to this, in this paper, we present our work only for a 3D tetrahedral mesh.Since the current straight walk algorithm is presented in a pseudo code form, as the first step for us to study it, we revisit the straight walk algorithm, and give it a mathematical description.Here we also review the required mathematical tools and concepts as well as the mathematical definition of the query point location problem.We then propose the flipping techniques to obtain an improved straight walk algorithm such that the straight walk algorithm works even for degenerate cases.Here we refer to a degenerate case as the one in which the current walk algorithm fails.To validate our improved straight walk algorithm, we fulfill the new algorithm in Python and then made numerical tests for several large scalecomplicated 3D meshes generated from a molecular surface and volumetric mesh generation program package, GAMer[12,13,14], for four proteins.Numerical results show that our improved straight walk algorithm works well for both normal and degenerate cases.
The remaining parts of this paper is organized as follow.Section 2 describes the current straight walk algorithm.Section 3 presents our improved straight walk algorithm.Section 4 reports numerical results.Conclusions are given in Section 5.
2 The current straight walk algorithm
LetS,Tandtbe a set ofnquery points, a tetrahedral mesh, and a tetrahedron(or cell)in R3, respectively.The query point location problem can be described as follows:
For eachq∈S,findt∈Tsuch thattcontainsq.
Its solution mainly relies on one mathematical tool called the orientation predicate, which is defined as the value of a 3×3 determinant:

In the straight walk algorithm[1], the query point location problem is solved in two steps — the initialization step and the walking step.A pseudo-code of this straight walk algorithm can be found in[1].According to it, we give the straight walk algorithm a mathematical description as follows.
In the initialization step, a start pointpis selected and a linepqis constructed.We then need to find a tetrahedron(or cell)of a meshTthat intersects the linepq.To do so, we randomly choose one cell withpbeing a vertex andua vertex not on the linepq,and denote byvandwthe other two vertices of the cell.We then search for a celltwhose verticesvandware located on the different sides of the planeuqpand satisfy the conditions
orientation(v,u,p,q)>0andorientation(w,u,p,q)≤0,
(1)
which implies that
orientation(v,w,p,u)<0.
Together with the conditionorientation(v,w,p,q)≤0,we find that the celltintersects linepq.See Figure 1 for illustration.Otherwise, we update bothvandwto get another cell and repeat the above checking process.

Figure 1 Points E and E′ are on the ‘positive’ and ‘negative’ sides of the plane determined by three points A,B,C, respectively, since orientation(A,B,C,E)>0 and orientation(A,B,C,E′)<0.

Figure 2 A normal case generated from the initialization step of the straight walk algorithm.Here the line segment pq intersects with the triangle uvw at an interior point A.
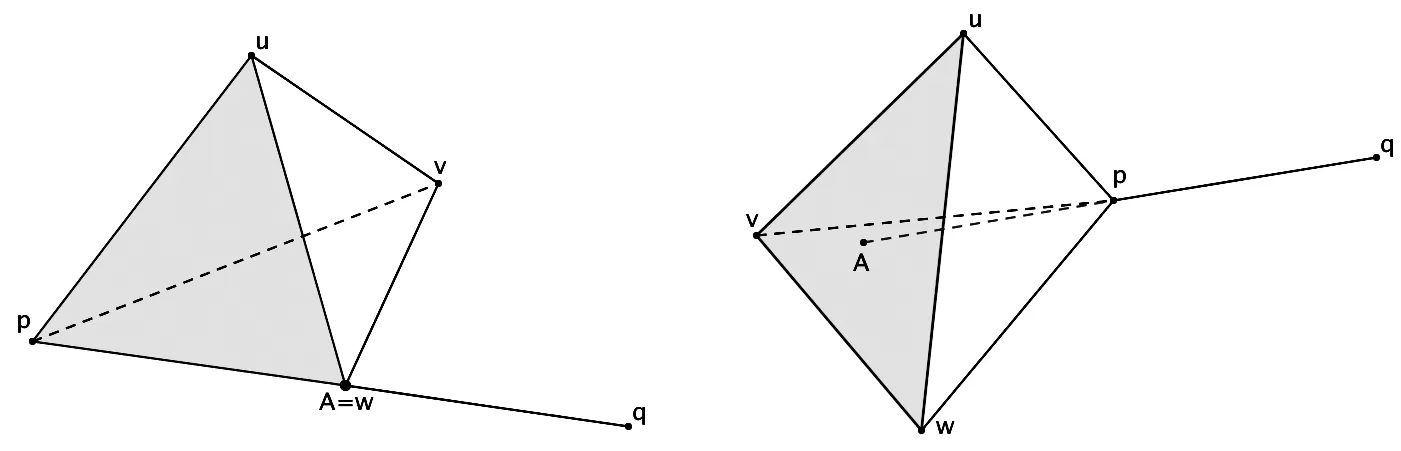
Figure 3 Two degenerate cases that may happen in the current straight walk algorithm:(a)the intersection point A coincides with the vertex w,(b)the intersection point A lies on the extended line of the line segment pq.
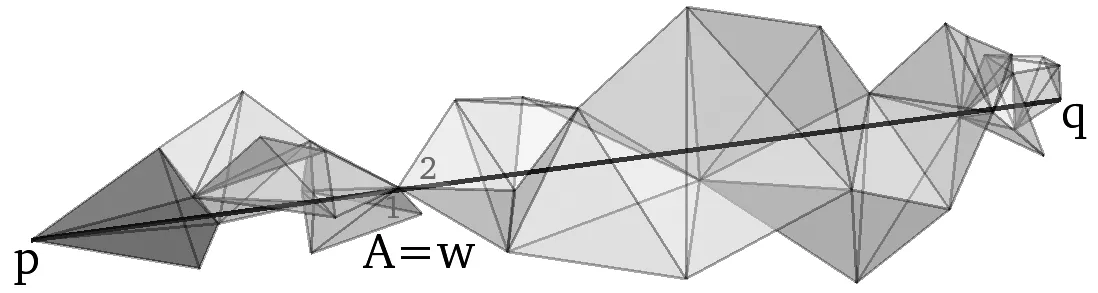
Figure 4 One walk process of our improved straight walk algorithm from the starting point p to the query point q in a 3D mesh.Here, one degenerate case happens at point w with A=w, and Cell 1 is flipped to Cell 2.
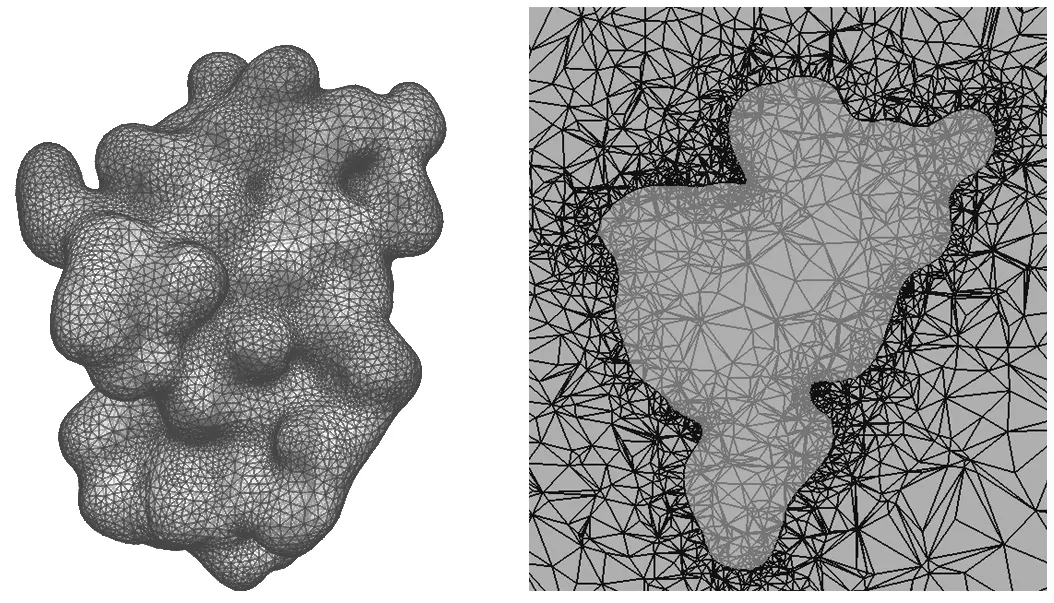
Figure 5 A tetrahedral mesh near the protein represented by the PDB ID FAS2.Here(a)a triangular mesh on the molecular surface of the protein, and(b)a cross section of the mesh around the protein.
In the walk step, starting with the cell found from the initialization step, we use the adjacent relations of cells with respect to a facet(or triangle)to traverse all the cells intersected by the line segmentpquntil we find the cell that contains the query pointq.The details of this step will be described in the next section together with our new modifications.
3 Our improved straight walk algorithm
During the initialization, we may either find the celltcontaining pointqor locate the celltthat intersects with the line segmentpqat the intersection pointAinside the triangleuvw(See Fig 1).In the former case, the search is completed, while in the later case, the walk step of the current straight walk algorithm can start normally.
However, in our numerical tests on the straight walk algorithm, we also observed that two degenerate cases might happen in the initialization step as illustrated in Fig 3.In a degenerate case of Case(a), the intersection pointAof a cell with the line segmentpqmay coincide with pointw(i.e.,the pointsp,w,qare on the same line).Thus, the next cell traversed by the linepqis not a neighbor of the previous one any more, which causes difficulties to find the cell we want using mesh adjacency relation and leads to the failure of the straight walk algorithm.If Case(b)happens, the straight walk algorithm fails too since the walk step might stop at a cell on the mesh boundary.
To deal with these degenerate cases, we make several modifications to the walking step by using flipping techniques.In particular, if the case(b)happens, we can simply flip the current celltwith respect to fixed vertexpsuch that the ‘new’ celltintersects with the line segmentpq.
Under the conditions in(1), we can verify thatorientation(v,w,p,u)<0 is equivalent toorientation(u,w,v,p)<0.Hence, iforientation(u,w,v,q)≤0,we find the celltcontainingq.
Iforientation(u,w,v,q)>0,thenpandqare on different sides of the plane determined by pointsu,w,v.However, we need to consider the following two cases:
1.If pointwis not on the planeupq,we can find a new adjacent celltthrough facetuwv.We then check whether the query pointqis on one facet of the new cell.If not, we need to judge if the only new vertexsof the current cell is on the line segmentpqor not.If yes, flip the current cell with respect to vertexs,setp=s,and choose the rest three vertices asu,w,vsuch that
orientation(v,u,p,q)>0,orientation(v,w,p,u)<0.
Otherwise, pointss,p,qare not on the same line.In this case, we simply follow the walk step in[1]without any change.
2.If pointwis on the line segmentpq,flip the current celltwith respect to vertexw,setp=w,and update the other three verticesu,v,w.
Here, we try to provide the pseudo-code for the improved 3D straight walk algorithm to make it more clear.At first, some notations used below need to be introduced:
1.neighbor(tthroughuvw)denotes the new tetrahedron that sharing the facetuvwwith the current tetrahedront;
2.w=vertex oft,w≠u,w≠v,w≠p,which meansu,v,pare vertices of the tetrahedrontand choosewas the fourth vertex oft;
3.coline(u,v,w)returns true if three pointsu,v,ware on the same line; otherwise, it returns false;
4.t,u,v,w=flip(twith respect to vertexp)means flipping the current celltwith respect to vertexpand then return the newt,which still containspas one vertex; meanwhile, we choose the other three new vertices asu,v,w,respectively, according to the properties that verticesu,v,ware supposed to satisfy in(1).
Our improved 3D Straight Walk algorithm is given as follows.
The improved 3D Straight Walk Algorithm(p,q)
//traverses the tetrahedral meshT,
//starting with vertexpto query pointq.
//t=uvwpis a tetrahedron ofT.
if orientation(vupq)* orientation(wupq)>0 {
if orientation(vupq)>0 {
v=w;
t=neighbor(tthroughwup);
w=vertex oft,w≠u,w≠v,w≠p;}
else {
w=v;
t=neighbor(tthroughwvp);
v=vertex oft,v≠u,v≠w,v≠p;} }
//nowvandwlie on different sides of planeupq,
//and switchwandvif necessary to make sure
//orientation(v,u,p,q)>0 and orientation(w,u,p,q)≤0.
while orientation(v,w,p,q)>0 {
t=neighbor(tthroughpvw);
s=vertex oft,s≠v,s≠w,s≠p;
if orientation(supq)>0v=s; else,w=s}
u=vertex oft,u≠v,u≠w,u≠p;
//End of initialization step
//and linepqintersects triangleuvw.
//To make sure line segmentpqintersects triangleuvw,
//do the following preprocessing with the flip technique.
t,u,v,w=flip(twith respect to vertexp);
while orientation(u,w,v,q)>0 {
if orientation(w,u,p,q)<0 {
t=neighbor(tthroughuvw);
s=vertex oft,s≠u,s≠v,s≠w;
if coline(s,p,q){
p=s;
t,u,v,w=flip(twith respect to vertexp); }
else {
if orientation(u,s,p,q)>0 {
if orientation(v,s,p,q)>0,u=s; else,w=s; }
else {
if orientation(w,s,p,q)>0;v=s; else,u=s; } } }
else {
p=w;
t,u,v,w=flip(twith respect to vertexp); } }
//tcontains query pointq.
Based on the straight walk algorithm, it is easy to show that this improved algorithm can eventually reach the cell containing the query point since each ‘walk’ process can be separated by several parts, each of which contains no degenerate case.Furthermore, Fig 4 displays such an example to show how our improved walk step works.Here, the line segmentpqis marked in blue, and the cells from the initialization and walk steps are colored in red and grey, respectively, throughout the whole walk process until the query pointqis located.From the figure we can see that a mesh pointwcoincides with the intersection pointAon the line segmentpq(i.e., the degenerate case(a)happens in the walk step), thus, we flipped cell 1 to cell 2 with respect to the fixed pointwso that the walk step can be continued.
It is tricky to flip a cell with respect to a fixed vertex to proceed the straight walk marching in the program.Some extreme cases may also happen, which we have to deal with.For instance, the line segmentpqmay intersect with the current cell at some interior point of an edge.But such case can also be similarly dealt with by properly selecting a vertex as the ’new’ start pointp,which we do not further consider here.
4 Numerical Tests
As a part of our project for solving an elliptic boundary value problem based on the finite element library DOLFIN[15], we programmed our improved straight walk algorithm in Python(http://www.python.org).To deal with the effects of truncated and round-off errors caused by “approximate” computation about the orientation test in the computer on our improved straight walk algorithm, the following test rule is used in the program: For a given toleranceε>0,four pointsa,b,c,dare considered to be coplanar provided that they satisfy
|orientation(a;b;c;d)|≤ε.
(2)
In all the tests reported here, a default valueε=10-10is used.
The four tetrahedral meshes that we select for tests are generated from a molecular surface and volumetric mesh generation program package, GAMer[12], for four proteins represented in the PDB identification numbers FAS2, BPTI, 1CID and 2AQ5, which can be downloaded from the protein data bank(http://www.rcsb.org).They are used by our finite element solver of an elliptic boundary value problem for the purpose of computing the solvation energy of protein in ionic solvent.As an example, Fig 5 displays a triangular mesh on the molecular surface of protein represented by FAS2 and a cross section of the tetrahedral mesh.From this figure we can see the complexity of the meshes that we used for tests.
In the tests, each query point setSconsists of the vertices of a mesh and the midpoints of all the edges of the mesh.The search starting pointpis fixed as one vertex of the first cell of a mesh for simplicity.To measure the performance of our improved straight walk algorithm, we calculate the following two average numbers:
(3)
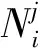
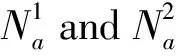
Table 1 Performance of our improved straight walk algorithm for four tetrahedral meshes generated from the program package GAMer[12]for proteins represented by PDB IDs FAS2, BPTI, 1CID and 2AQ5.Here are defined in(3)
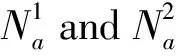
5 Conclusion
In this paper, we revisited the straight walk algorithm proposed in[1], and gave it a mathematical description to make it easy to be understood.Then we proposed an improved straight walk algorithm such that the straight walk algorithm works well in several degenerate cases.Our improved straight walk algorithm was numerically tested for complicated 3D meshes used in the continuum model’s simulation and the numerical tests showed that it works well not only for the normal cases, but also for the degenerate cases, which demonstrates the effectiveness of the flip technique and the improvements of the new walk algorithm.
