基于状态不确定性的动态滤波算法
2020-06-03
(中南大学 数学与统计学院,长沙,410083)
1 引言
在大地测量数据中经常存在不确定性,它们影响着参数估计的准确性.不确定性是广义的误差,它包含可度量和不可度量的误差[1-3].测量数据的不确定性可以是具体数值,也可能它们仅在一定的实数区间内变动,又或许是个模糊数.利用先验信息来抑制不确定性是不确定性观测数据平差的有效方法.在实际处理中可根据先验信息建立对参数的约束条件[4-7],即状态参数的不确定性.
近年来,针对状态约束的动态问题已经有了许多深入的研究,主要的方法有:水平滑动估计法[8-10]、平滑约束卡尔曼滤波[11]、二阶泰勒级数展开非线性约束滤波[12]等.文献[13,14]将不等式约束模型转化为规划问题求解,文献[15]提出了内点法,将约束问题转换成无约束问题.文献[16]用一系列二次规划子问题代替原带约束问题.文献[17]将不等式约束转换为椭球约束利用岭估计计算,解是有偏的,并且不一定能满足不等式.将不等式约束函数转换为概率密度函数是另一种方法,但是其计算量随着状态维数迅速增大[18].杨元喜等引进自适应因子建立自适应抗差滤波理论[19,20],提出带约束的抗差卡尔曼滤波模型[21].文献[22]推导了等式约束卡尔曼滤波的解及其统计性质,指出附不等式约束和等式约束卡尔曼滤波问题的解具有相同的性质.然而上述算法并没有有效利用已知的观测信息,未给出显示表达式,且计算量巨大.对于状态约束仅考虑了等式约束和不等式约束,椭球约束的滤波模型并没有得到讨论.基于此,本文将状态参数的不确定性定义为状态约束,把已知的观测信息与平差准则结合,转化为具有约束的规划问题,利用拉格朗日乘数法求解,推导出无约束、不等式约束和椭球约束下的滤波算法.
2 无约束滤波算法
在无状态约束时,考虑下面的滤波模型
xk=Φk,k-1xk-1+wk,
Lk=Hkxk+vk,
其中状态向量xk∈n,观测向量Lk∈m,Φk,k-1是状态转移矩阵,Hk为m×n阶系数矩阵,wk∈n和vk∈m分别为状态噪声和观测噪声向量,且满足
Ewk=0,Evk=0,

令
(1)
(2)
对滤波模型建立平差准则
(3)
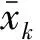
我们有
(4)
式(4)即为卡尔曼滤波模型中状态估计的递推公式.
现在将平差准则(3)变为如下形式
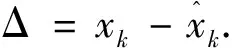
(5)
忽略与xk的无关项,平差准则(5)可写为
(6)
其中
(7)
对式(7)求逆有
(8)
因此我们得到无约束滤波算法:
无约束滤波算法与卡尔曼滤波公式是一致的,式(8)是Pk的递推公式,式(6)是度量测量信息L0,L1,…,Lk对状态xk的影响.
3 不等式约束滤波算法
在平差测量中状态参数的不确定性可表示为区间约束(如某些状态参数大于零),因此有不等式约束模型
xk=Φk,k-1xk-1+wk,
Lk=Hkxk+vk,
Gkxk≤qk.
相应的不等式约束下的平差准则最优化问题为
(9)
s.t.Gkxk≤qk.
为求解此最优化问题,构造广义Lagrange函数
(10)
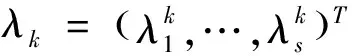

G1kxk=q1k,
和
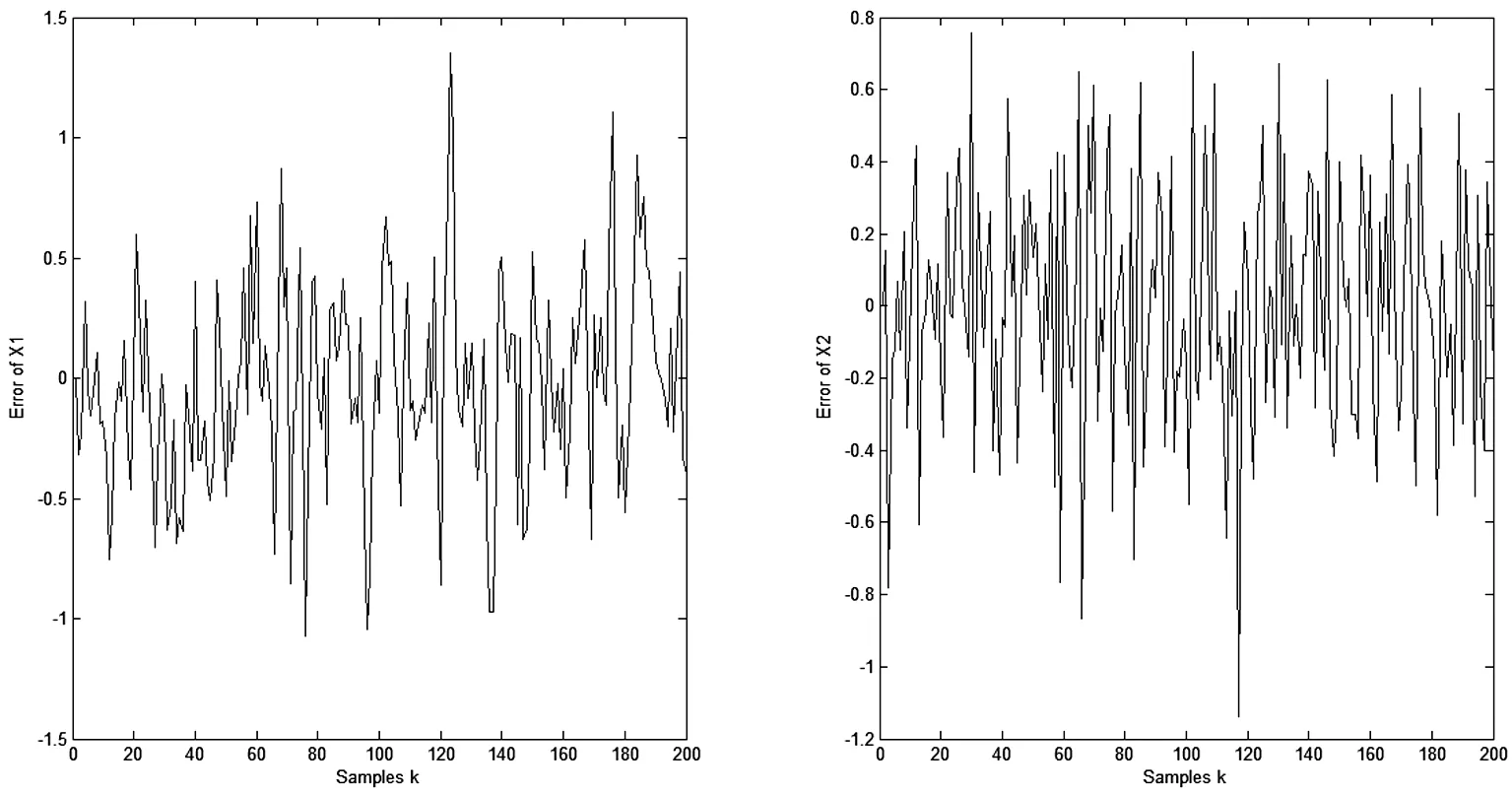
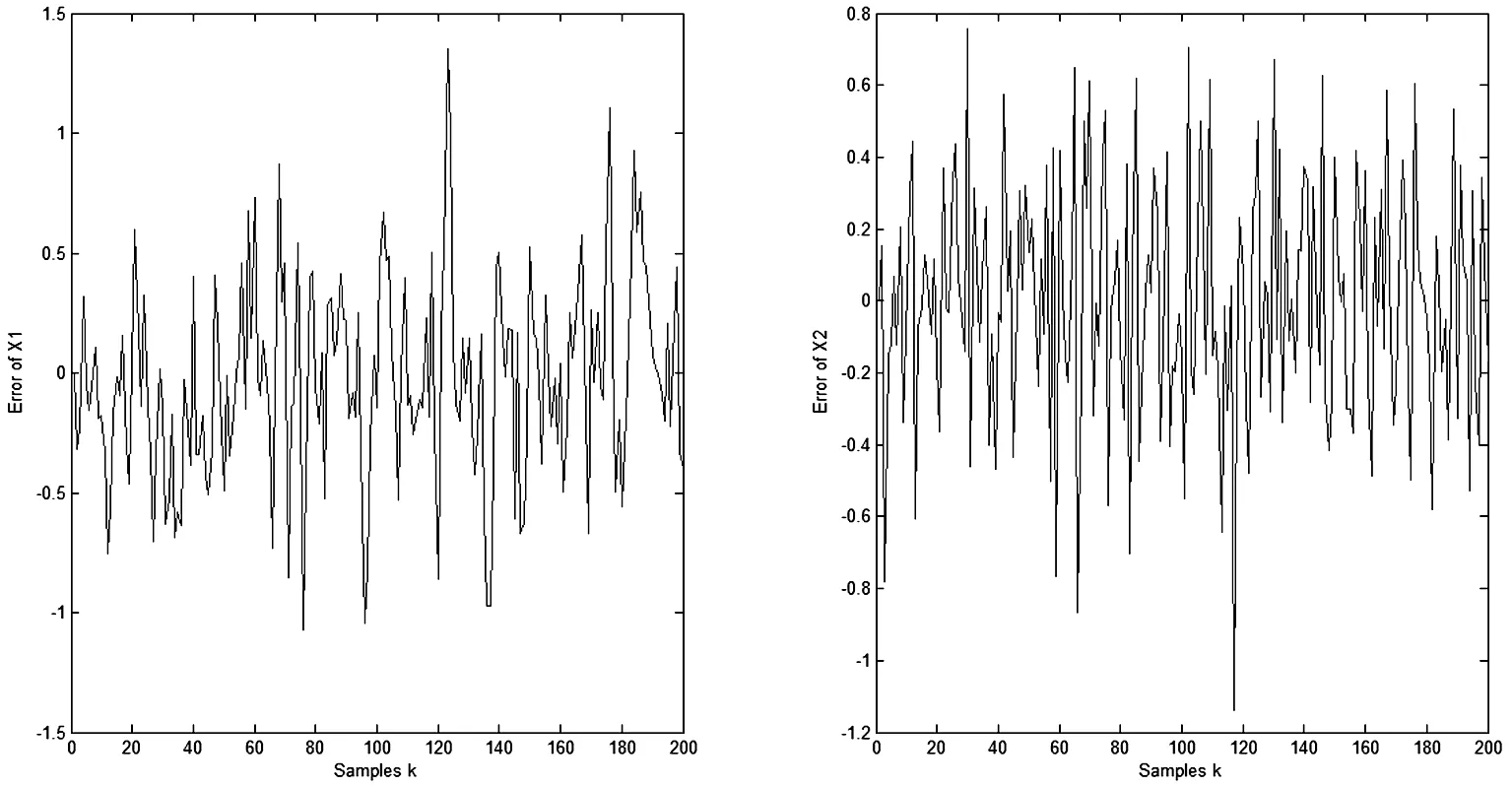
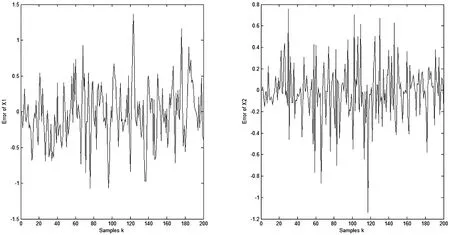
G2kxk 令 (11) 则有 (12) (13) 由(11)和(12)式,并忽略式(12)中与xk无关的项,得到如下的平差准则 (14) 式中 (15) 因此不等式约束滤波算法为: 式(12)是不等式约束滤波解的递推估计方程,式(15)是Pk的递推公式,式(14)是度量测量信息L0,L1,…,Lk对状态xk的影响. 滤波模型中状态参数存在椭球约束的滤波模型可表示为 因此椭球约束下的最优化问题为 (16) s.t.Lk=Hkxk+vk, 为求解此问题,构造广义Lagrange函数 (17) 式中μk≥0.求解式(17)可得 (18) (19) (20) 其中 (21) 平差准则(21)经过适当变形,并忽略与xk无关的项可表示为 (22) 其中 (23) 因此椭球约束滤波算法为: 式(20)是椭球约束滤波解的递推估计方程,式(23)是PCE,k的递推公式,式(22)是度量测量信息L0,L1,…,Lk对状态xk的影响. 为了检验算法的有效性和性能,考虑下面的二元状态变量的滤波模型 图1 标准卡尔曼滤波算法的误差 从图1、图2看出,无约束滤波算法与标准卡尔曼滤波算法中的x1和x2的误差值并无差别.图3和图4表明,当考虑状态参数不等式约束和椭球约束的不确定性时,本文提出的不等式约束滤波算法和椭球约束滤波算法能有效地利用这一先验信息对状态进行估计.整体来看不等式约束滤波算法的估计误差略大于无约束滤波算法,但整体误差趋势一致.而椭球约束滤波算法的估计误差小于无约束滤波算法,估计效果最佳. 图2 无约束滤波算法的误差 图3 不等式约束滤波算法的误差 图4 椭球约束滤波算法的误差 为了更加清晰地比较不同滤波算法的性能,本文进行了1000次蒙特卡洛模拟实验,结果见表1.通过比较不同滤波模型的RMS值发现:无约束滤波算法与卡尔曼滤波算法具有一致性.椭球约束滤波算法比无约束滤波算法能更准确地进行状态估计.而不等式约束滤波算法的RMS值略高于其余三种滤波算法. 表1 不同状态约束滤波算法的RMS比较 在实际测量中,状态参数的不确定性不能被忽略.本文利用状态约束这一区间形式表示状态参数的不确定性,基于平差准则并结合状态方程分别建立无约束、不等式约束和椭球约束滤波模型,并运用已知观测信息,将模型化为规划问题求解,最终推导出的无约束滤波算法、不等式约束滤波算法和椭球约束滤波算法的显式表达式.其中无约束滤波算法与卡尔曼滤波算法具有一致性,且三种模型最终具有统一的平差准则.仿真实验结果表明:三种模型均能准确地进行状态估计,并且运算高效、简便.

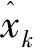
4 椭球约束滤波算法



5 仿真实验




6 结论
