基于ADAMS的太阳能清灰机械推拉机构的仿真

李进韬，龚 俊，2,宁会峰，2，李翠明，2，康 儒

(1.兰州理工大学机电工程学院，甘肃 兰州 730050)(2.兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃 兰州 730050)

随着能源危机日益严重、环境污染日益加剧，新能源的开发与利用越来越受到关注。太阳能光伏发电作为重要的清洁能源得到了重视，近年来取得了极大的发展，但太阳能光伏板上的落灰严重制约了发电效率，因而很有必要研制开发一款效率高、成本低、自动进行灰尘清洁的机械。本文主要是对一种新型太阳能清灰机械的关键机构——推拉机构进行动力学研究，以便为清灰机械的流量控制及其他相关部件的结构设计、强度校核、整车的灵敏性以及稳定性测试提供具体的设计参考依据。该推拉机构实质是导杆机构，现有的导杆机构的运动学和动力学分析方法有作图法[1]和计算法[2]两种：作图法直观、方便，但精度不高，需要反复作图；计算法人工计算量大，容易出错。采用计算法时，使用ADAMS软件不仅可以生成复杂机械系统的虚拟样机，有效地仿真其运动过程，精确度高，而且将计算工作交给计算机能省去大量人工，并且不容易出错。

1 太阳能清灰机械推拉机构的总体设计

太阳能清灰机械主要由车体、水平移动装置、竖直移动装置、液压缸推拉装置、刷体清灰装置等几部分构成，如图1所示。其中，水平移动装置用来补偿车体偏离光伏板的水平距离，竖直移动装置用来适应不同高度的太阳能光伏板的清灰，通过液压缸推拉装置将刷体清灰装置旋转至与水平面成37°(太阳能光伏板电站中太阳能光伏板的安装角度与水平地面成37°)，它是整个设备中的关键结构。由于太阳能光伏板自身长为4 060 mm，这就要求刷体的长度也为4 060 mm。整个设备工作时是处于偏心状态的，其中推拉机构的设计关系到整台设备是否可以实现刷体清灰装置与水平面成37°的目的和整台设备受力是否合理。

图1 太阳能清灰机械总体结构示意图

1.1 推拉机构的工作原理

推拉机构由两个平行液压缸、刷子与主梁的总装体、连接架(基体)等组成，是一个摆动导杆机构，其工作原理如图2所示。推拉机构分为非工作和工作两个状态。当液压缸不进油时，机构处于非工作状态，当液压缸进油至液压缸处于最大行程时，机构处于工作状态，此时刷体与主梁的总装体与水平面的夹角为37°。

图2 推拉机构的工作原理示意图

1.2 推拉机构的结构设计

按照1.1中工作原理所设计的推拉机构实质为一导杆机构，其具体结构如图3所示。在推拉的过程中，已知推角的变化角度γ12=48.47°，缸的初始长度H=1 070 mm,机架的长度S=1 144 mm，液压缸的行程L=800 mm，由式(1)和式(2)可推导出：E=1 288 mm,γ1=61.83°。

(H+L)2=S2+E2-2EScos(γ1+γ12)

(1)

(2)

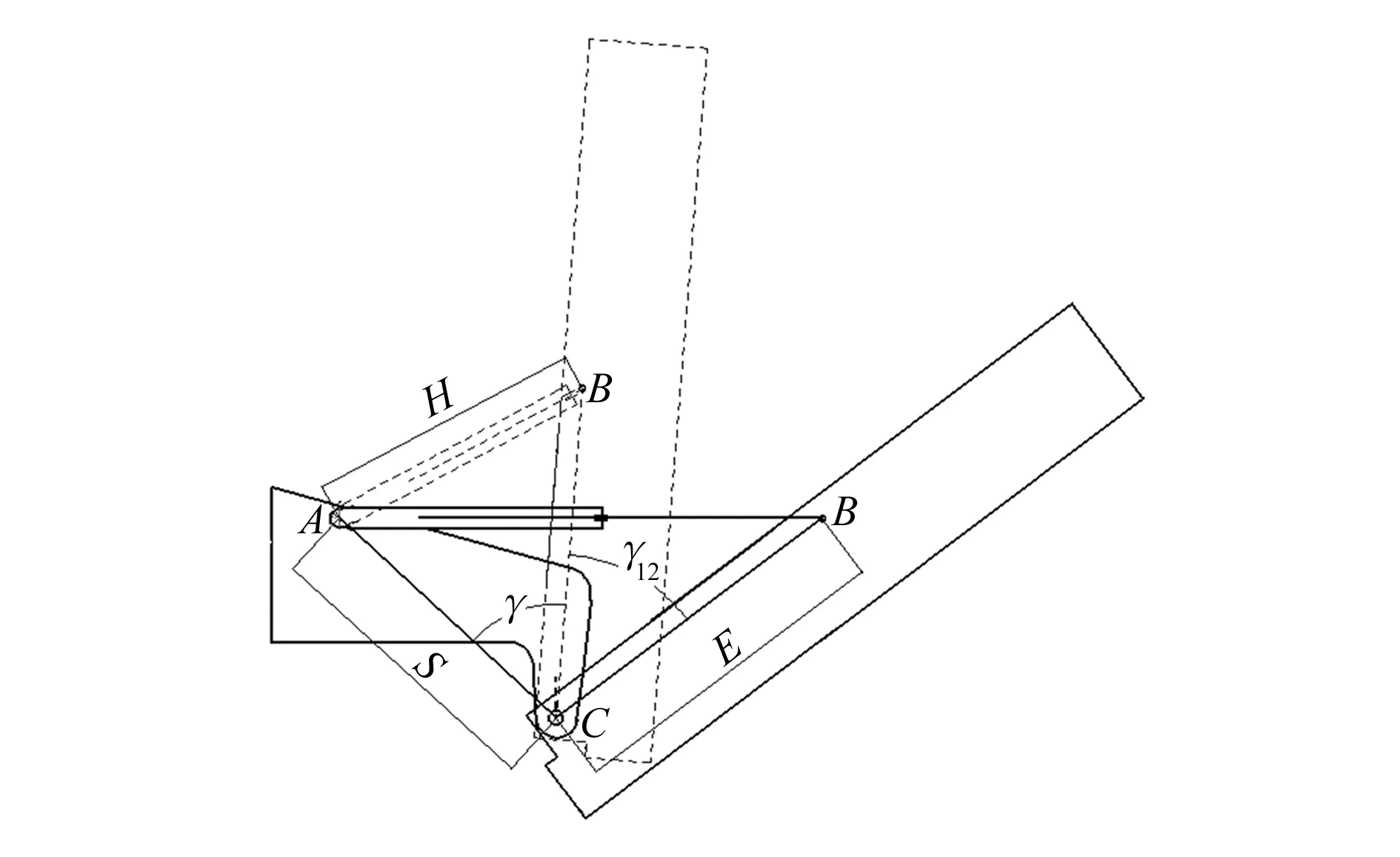
图3 导杆机构工作示意图

2 导杆机构运动学方程的建立

2.1 导杆机构的速度分析

为模拟实际工作过程中油缸进油的规律，将活塞杆的推出速度分为3个阶段：变加速阶段、匀速阶段、变减速阶段。采用三次多项式逼近海赛阶跃函数Step来定义活塞杆的推出速度，Step在ADAMS中的表达式[3]为

Step(X，X0，H0,X1，H1)=

(3)

式中：X为自变量，XX1时，因变量为终止值H1；X0≤X≤X1时，因变量应根据一定规律光滑过渡，避免出现竖直过渡突变、微分值不连续。

将式(3)中的X用时间t代替，且X0=3.165 s,X1=26.665 s,H用活塞杆的推动速度v代替，则变为速度与时间的函数，可得到Step(time,0,0,3.165,30)+Step(time,3.165,0,26.665,0)+Step(time,26.665,0,29.83,-30)的曲线图，即活塞杆速度v随时间t变化的规律，如图4所示。

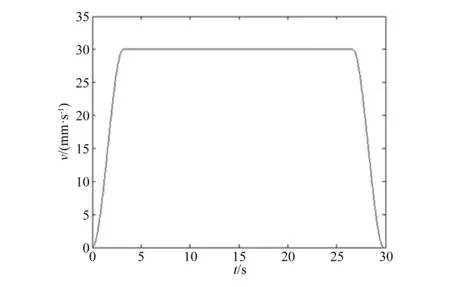
图4 活塞杆速度v随时间t变化的规律

导杆机构[4]工作过程中，液压缸实际长度M是油缸的闭合长度H(油缸活塞杆不伸出时的原始长度)和经过t秒后油缸活塞杆的伸出长度之和，即：

M=H+vt

(4)

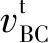
(5)

(6)

导杆机构的速度分析如图5所示。

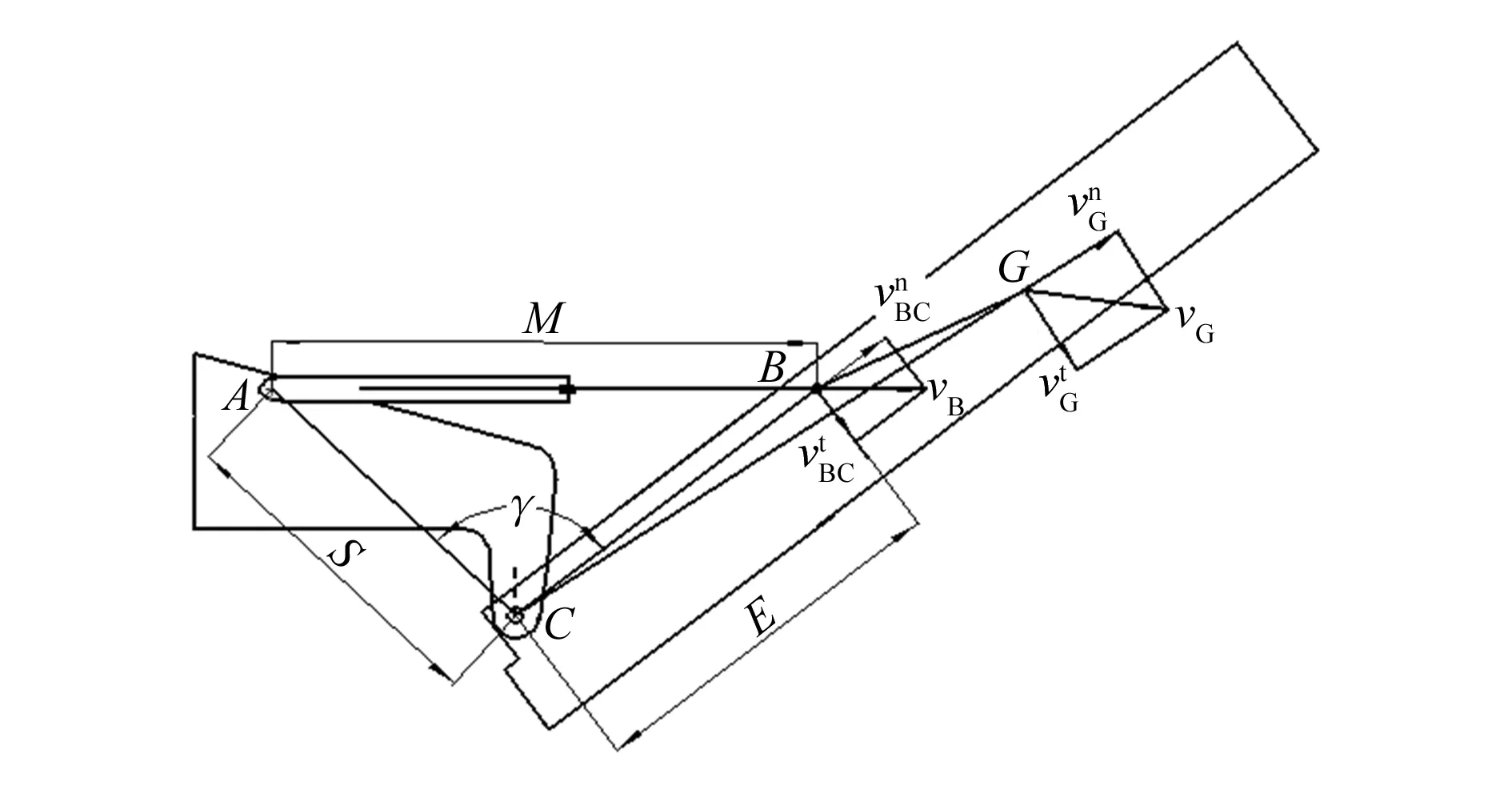
图5 导杆机构的速度分析示意图

2.2 导杆机构的加速度分析

在进行导杆机构的加速度分析[5]时做如下假设：

1)推拉机构的液压系统必须保证刷体与主梁的总装体在29.83 s时间内完成由静止开始至最终总装体始终与水平面成37°角；

2)刷体和主梁总装体(看成一个部件)重心在G处。

总装体绕铰接点C旋转的角度γ满足关系式(7)，并且当t=0 s时，γ=61.83°；t=29.83 s时，γ=110.30°。

(7)

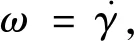
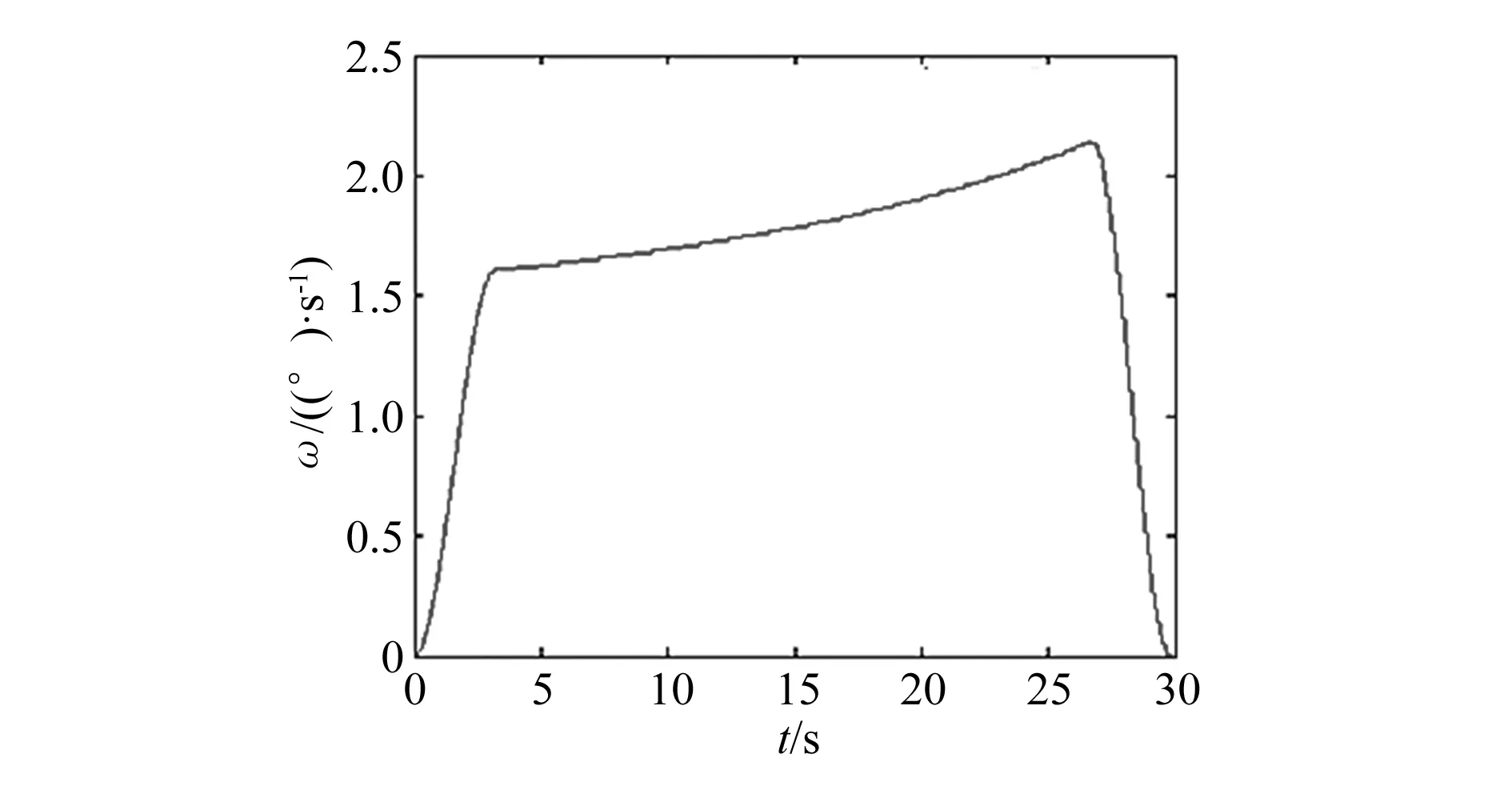
图6 总装体转动的角速度随时间的变化规律

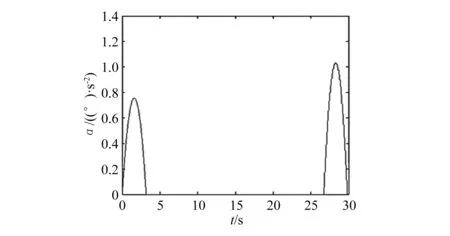
图7 总装体转动的角加速度随时间的变化规律

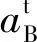
(8)

(9)

设重心G处的加速度为aG，由图(5)可知：

(10)

(11)

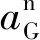
(12)

因此，总装体的G点处加速度aG为：

(13)

导杆机构的加速度分析示意图如图8所示。

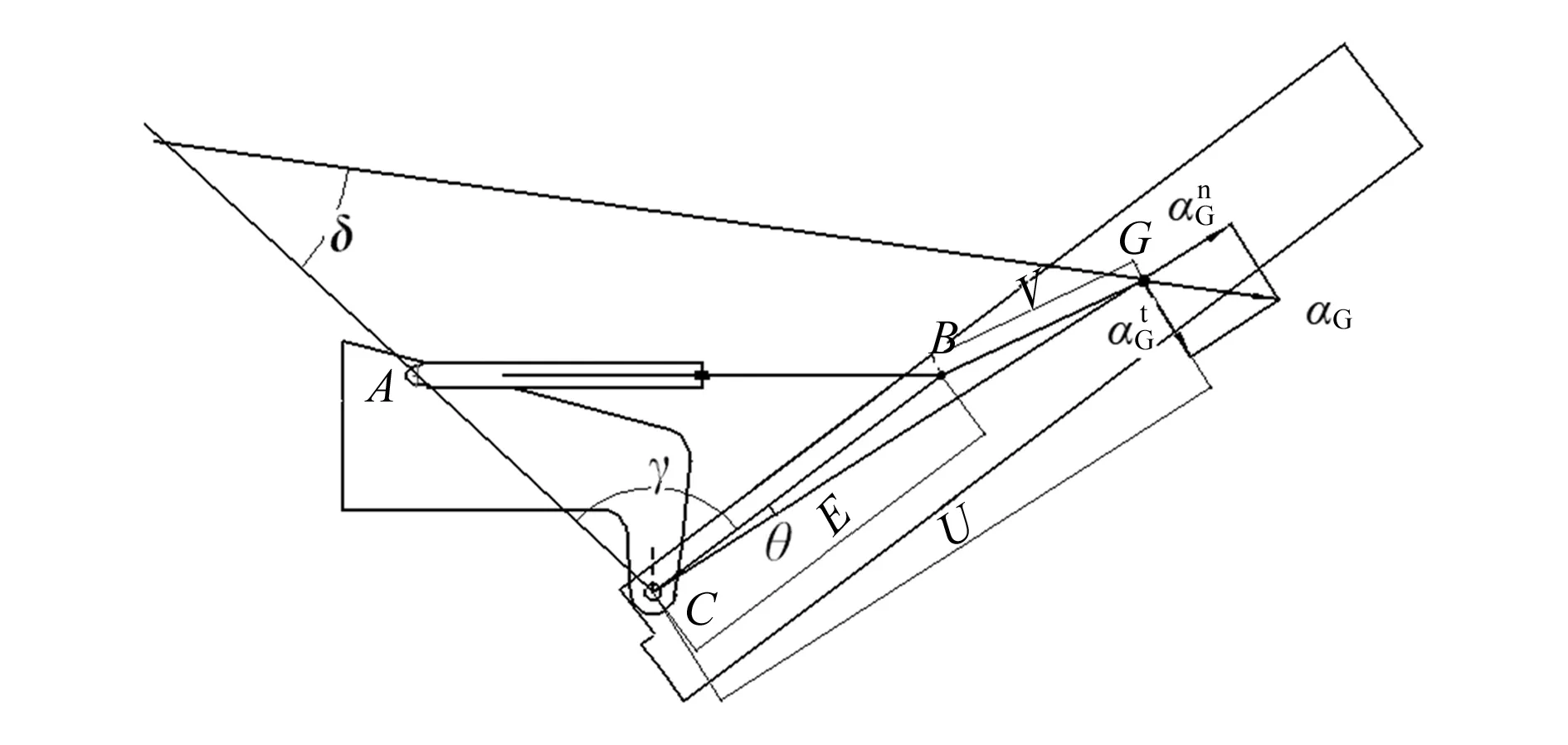
图8 导杆机构的加速度分析示意图

刷体G处的加速度aG的方向角δ：

(14)

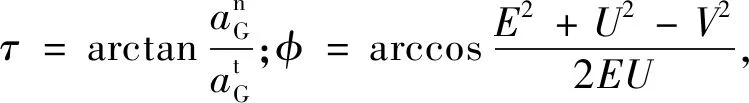
3 基于ADAMS的推拉机构运动学模型和仿真分析

3.1 推拉机构虚拟样机的建立

利用Pro/E建立推拉机构的三维模型，将模型导入到ADAMS中[6]，并在各个铰接点处添加运动副，添加各构件的材料、质量属性，最后构造出推拉模型的虚拟样机模型，如图9所示。

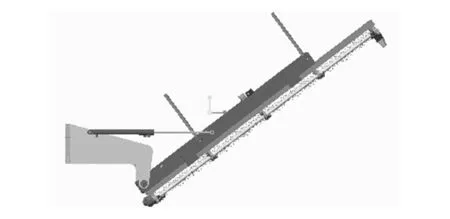
图9 推拉机构的三维虚拟样机模型

3.2 推拉机构驱动函数的确定

为保证在推拉过程中推拉机构有较好的启动和制动性能，选择Step函数定义油缸的驱动速度。油缸的驱动特性[7-8]定义如下：在t=0 s时，活塞杆的速度为0 mm/s；在0—3.165 s，活塞杆相对于油缸的速度由0 mm/s增加到30 mm/s；在3.165—26.665 s，活塞杆的相对速度保持30 mm/s不变；在26.665—29.830 s，相对速度由30 mm/s减小到0 mm/s。由驱动定义过程可以得出推拉机构的Step驱动函数为Step(time,0,0,3.165,30)+ Step(time,3.165,0,26.665,0)+ Step(time,26.665,0,29.83,-30)。

在ADAMS中完成的驱动函数定义得到的推拉机构的驱动特性曲线如图10所示。由图可知，推拉机构的驱动特性满足本文对Step函数的设计要求。

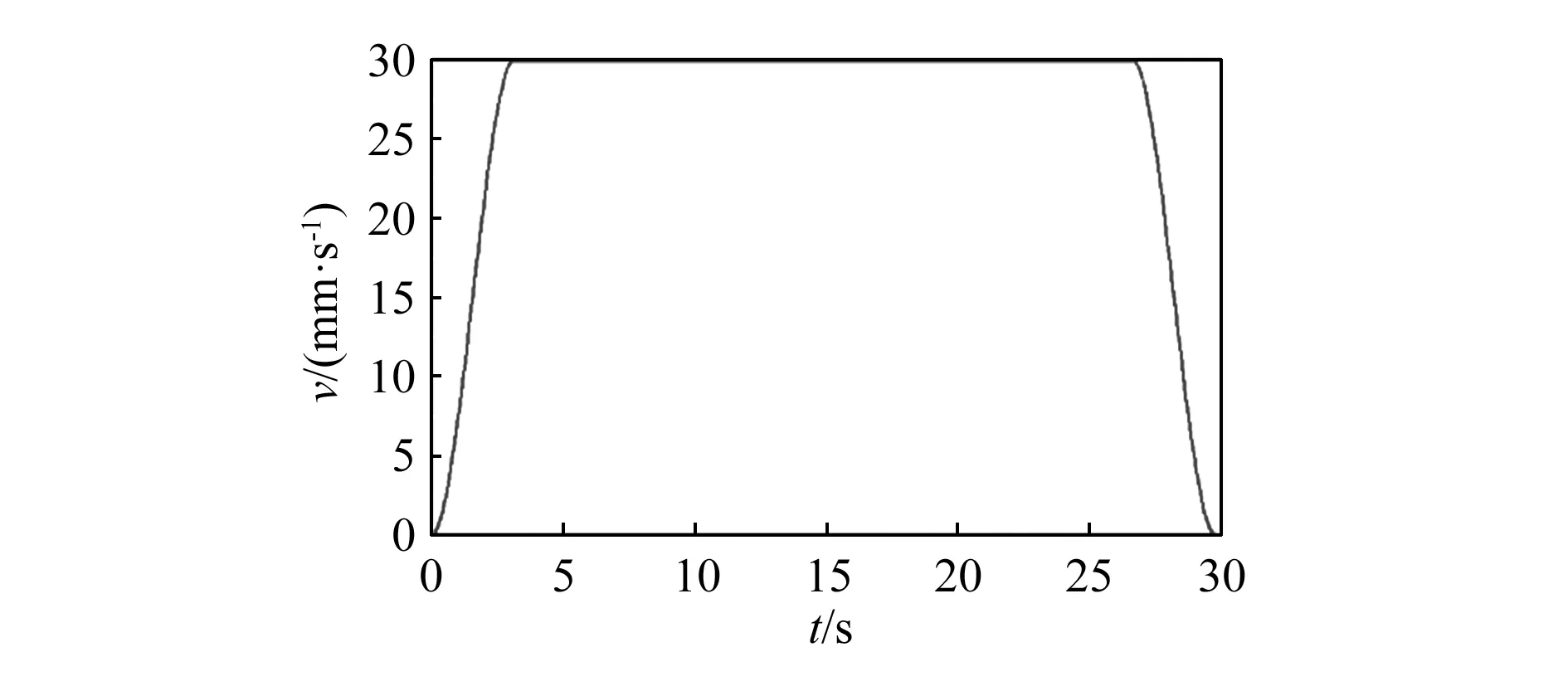
图10 推拉机构的驱动特性曲线

3.3 仿真结果分析

3.3.1刷子与主梁总装体的角速度与角加速度分析

液压缸活塞推杆在30.000 s时到达最大行程处，得到总装体的最大转角为48.463°，与1.2中推角的变化值γ12=48.47°对应，此时刷体与水平面成36.79°，在误差允许范围内。在推举过程中，液压缸的最大转角发生在29.830 s，仅为28.08°，可以看出在推举过程中液压缸的转动量很小，这对于液压缸的平稳工作很有利。

图11和图12是总装体的角速度与角加速度曲线图，由图可以看出它与1.2中建立的数学模型曲线大体吻合，其中最大角速度发生在26.655 s，但是整个运动过程平滑过渡，没有突变，说明推举效果好；最大角加速度发生在最后变减速阶段的28.450 s，仅有1.03 (°)/s,这说明在总装体整个转动过程中，转动惯性小，转动比较平稳，对于铰接处的冲击小。

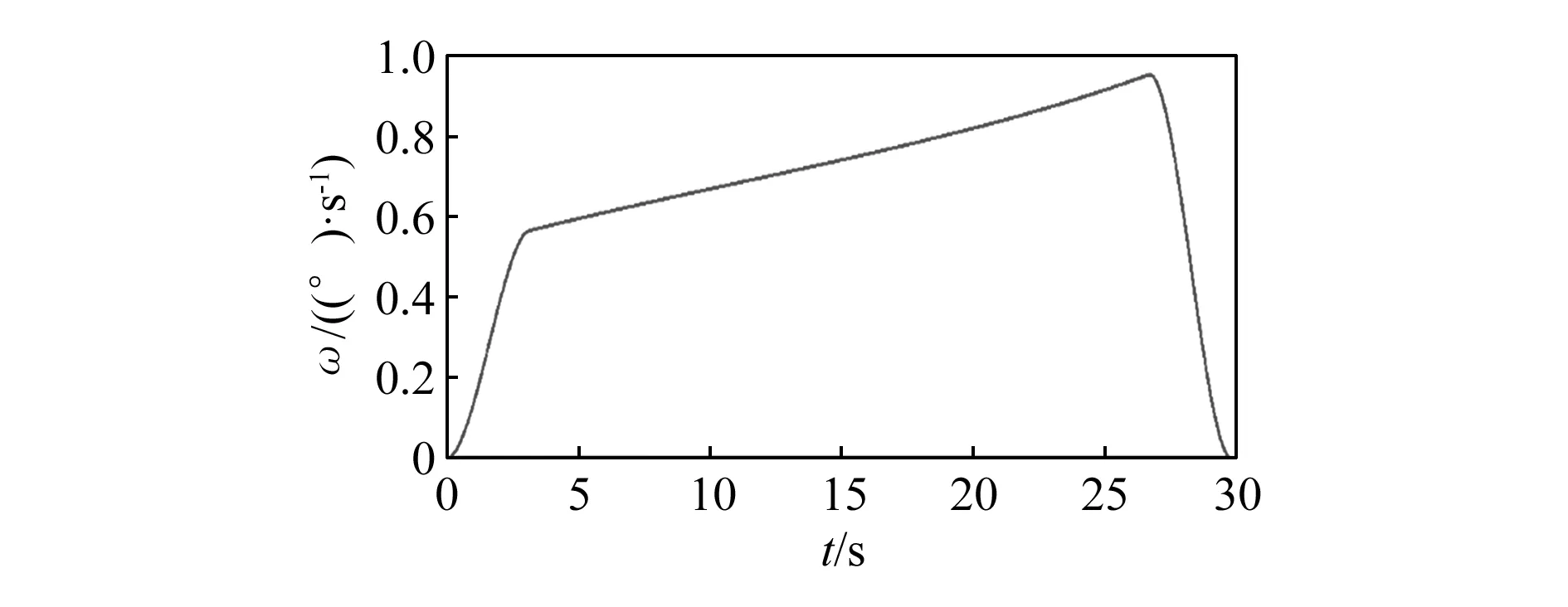
图11 推拉机构中总装体角速度曲线图

3.3.2刷子与主梁的总装体的速度和加速度分析

图13和图14为总装体质心处的速度与加速度的曲线图，可以看出在推拉机构推举过程中总装体的速度和加速度曲线走势平稳无突变[9]，说明它的推举性能好。同时，在推举的开始和终止阶段，速度平稳过渡，加速度的数值不大，也说明在推举过程中，推拉机构的启动和制动的性能好，对整车的惯性冲击和瞬时冲击[10]都很小，能够满足实际的工作需要。

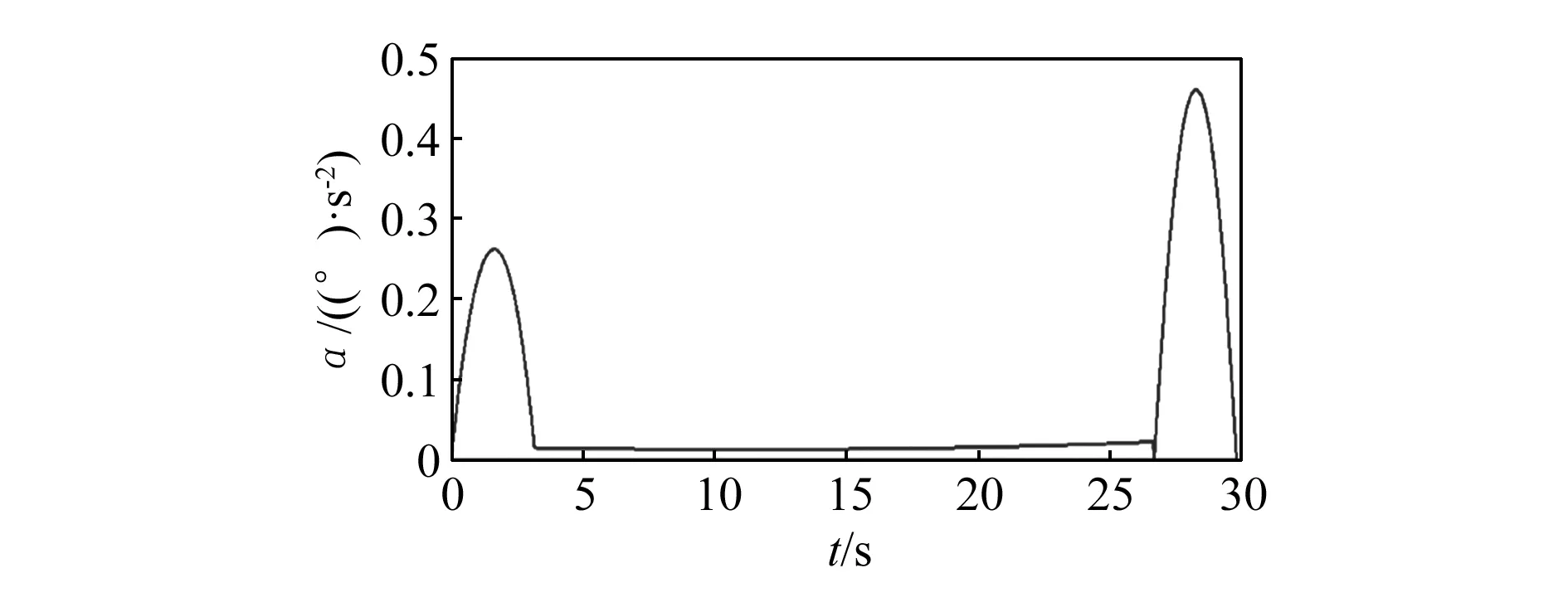
图12 推拉机构中总装体角加速度曲线图

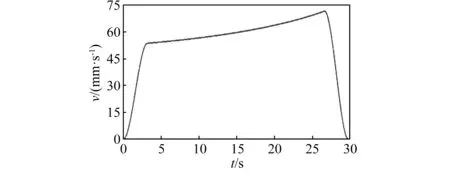
图13 推拉机构中总装体速度变化曲线图

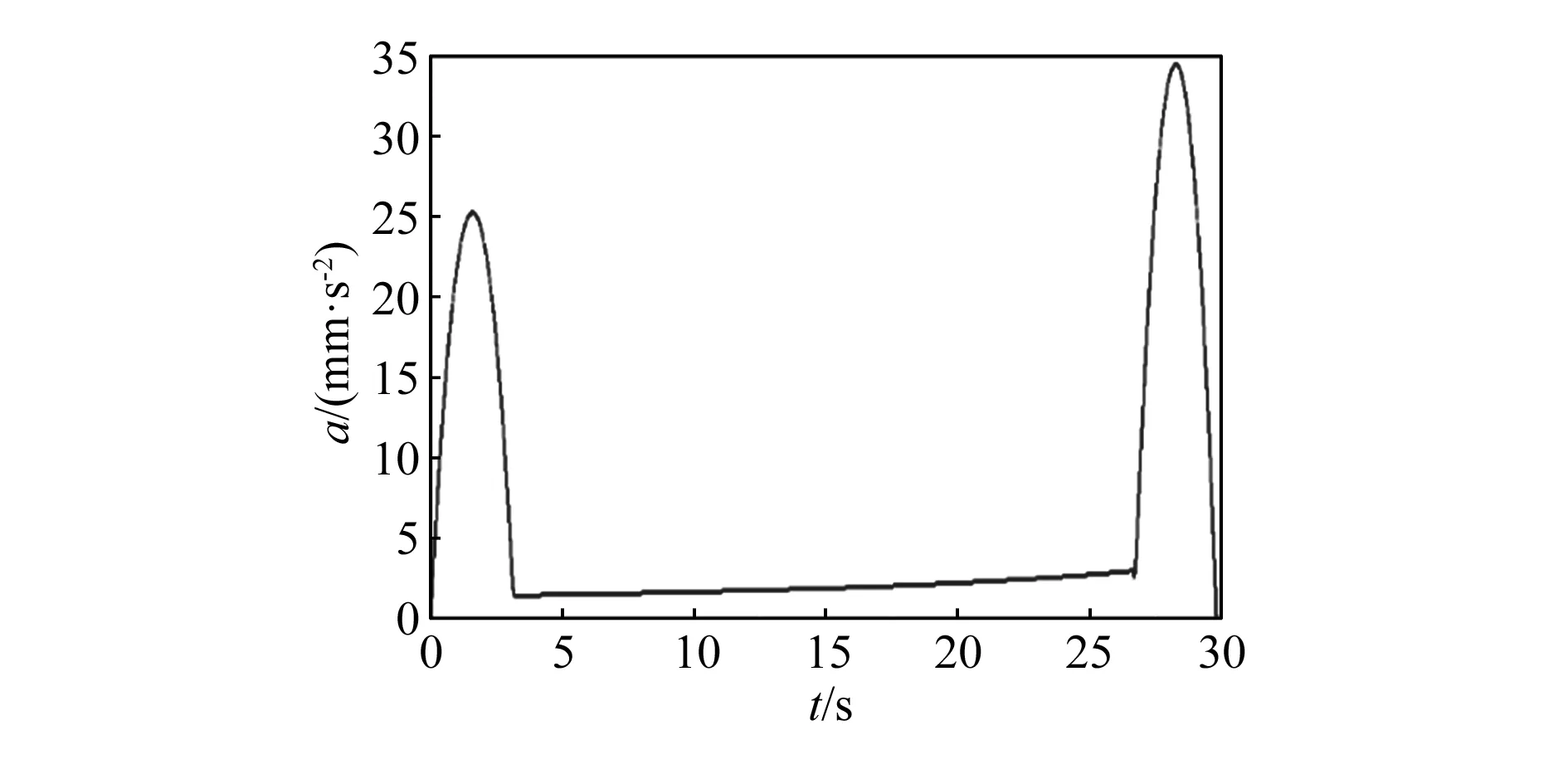
图14 推拉机构中总装体加速度变化曲线图

3.4 推拉机构中各个铰接点处受力曲线分析

图15～17是液压缸体与主梁的铰接点、液压缸的活塞推杆与连接架的铰接点、梁与连接架的铰接点在液压缸推举过程中的受力曲线图，由图可以看出推拉机构随着活塞推杆的运动，各个铰接点所受的力在逐渐增大，并且没有突变的现象，说明在这个过程中各个铰接点受力是平稳的，不会出现瞬间突变的载荷对铰接处的轴造成破坏；此外还可以看出各铰接点处的最大力都出现在t=30 s,且主梁和连接架的铰接处所受的力是最大的，这说明在整个推拉机构中，此处是危险断裂点。

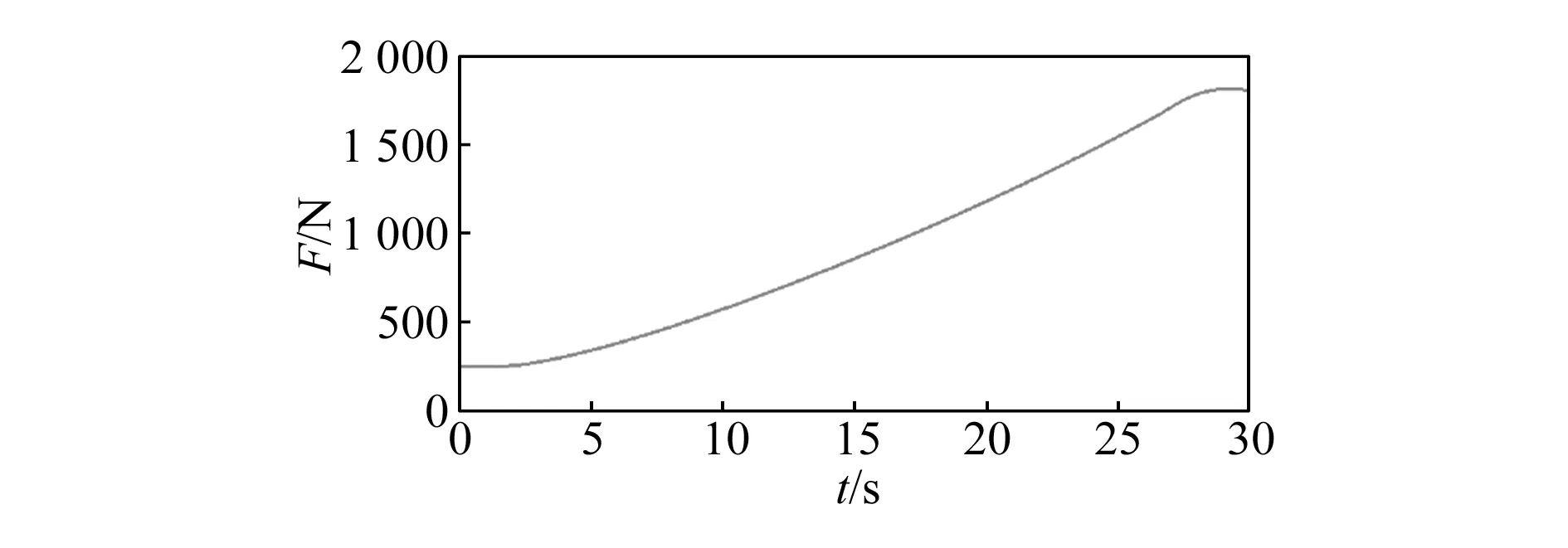
图15 液压缸体与主梁的铰接点受力变化曲线图

图16 液压缸的活塞推杆与连接架的铰接点受力变化曲线图

图17 梁与连接架的铰接点受力变化曲线图

4 结论

1)根据本文建立的推拉机构运动模型，结合实际工作中油缸的进油规律，采用三阶样条插值函数模拟活塞杆的速度运动规律，运用MATLAB软件得到的角速度和角加速度的曲线，与ADAMS模型中角速度和角加速度曲线一致，从而能够检测用经验设计的产品是否符合实际要求。

2)通过对主梁和刷子总装体质心速度和加速度进行分析，可知整个推拉机构在运动过程中加速性能以及运动性能平稳；通过对整个机构在运行过程中各部件的受力情况分析出了各部件的薄弱环节，可为今后具体部件的结构设计提供参考。