λ对曲柄摆动导杆机构的运动特性影响

冯立艳，何世伟

(华北理工大学 机械工程学院，河北 唐山 063210)

λ对曲柄摆动导杆机构的运动特性影响

冯立艳，何世伟

(华北理工大学 机械工程学院，河北 唐山 063210)

曲柄摆动导杆机构；运动特性；角速度；极位夹角

曲柄摆动导杆机构的运动性能取决于特性系数λ。研究了曲柄摆动导杆机构的极位夹角分别为锐角、直角、钝角时λ的取值范围；建立了λ与极位夹角θ、行程速比系数K、导杆的摆角φ3、角速度ω3、角加速度α3之间的数学关系式，求得了φ3及ω3最大时λ的取值，并绘制了对应的曲线图，进一步分析了λ对曲柄摆动导杆机构运动特性的影响，为曲柄摆动导杆机构的设计提供了重要的理论依据。

曲柄摆动导杆机构在牛头刨床等机械中得到了广泛应用，它将曲柄的旋转运动转换为导杆的往复摆动，并具有急回特性[1,4-5]。邸海燕等[2]用解析法建立了曲柄摆动导杆机构的运动学数学模型,并借助MATLAB绘制了其运动规律的可视化图形。同时，目前国内许多教材将极位夹角描述为“当从动件在两极限位置时，对应的主动曲柄两位置之间所夹的锐角[5]”，这是不准确的，因作者在研究中发现，曲柄摆动导杆机构的极位夹角不一定为锐角，还可能为直角、钝角，它取决于机架长度与曲柄长度的比值λ，且导杆的运动学性能也直接与λ有关。该项目深入研究了λ与极位夹角θ、行程速比系数K、导杆的运动规律及运动特性之间的关系。

1 曲柄摆动导杆机构的主要特征

曲柄导杆机构是由曲柄滑块机构演化而来的。如图1(a)所示的曲柄滑块机构中，若改选构件AC为机架，此时构件3绕轴C点转动，而构件2则沿构件3相对移动，构件3称为导杆，此时机构为曲柄导杆机构，如图1(b)。由曲柄滑块机构的曲柄存在条件可知，若AC≤AB，则导杆3能作整周转动，称为曲柄转动导杆机构；若ACgt;AB，则导杆3仅能绕C点摆动，则称为曲柄摆动导杆机构[4]。

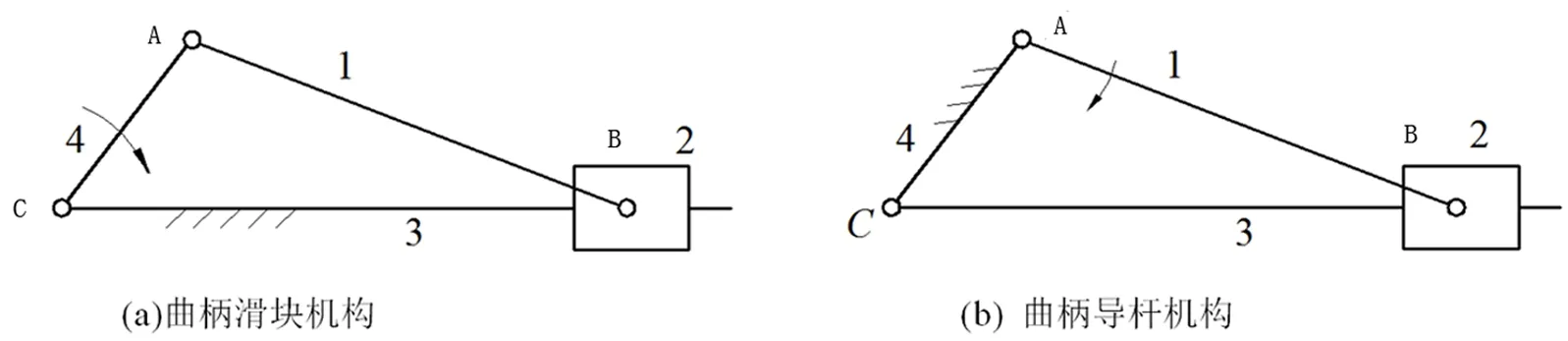
图1 曲柄滑块机构演化为曲柄导杆机构

如图2所示为曲柄摆动导杆机构，导杆的2个极限位置为CB1和CB2，导杆的摆角为ψ，机构的极位夹角为θ。

图2 曲柄摆动导杆机构及其极限位置

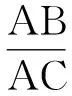
(1)

2 特性系数λ与行程速比系数K的关系

机构急回程度的大小用行程速比系数K表示，K越大，急回程度越显著，K与θ有如下关系[4]，：

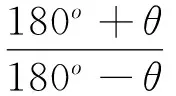
(2)

将式(1)代入(2)，得：

(3)

图3 K-λ曲线

根据式(1)、(3)，得出θ分别为锐角、直角、钝角时，λ和K的取值，如表1所示。

表1 当θ分别为锐角、直角、钝角时λ的取值

3 特性系数 对导杆机构运动性能的影响

现推导特性系数λ与导杆摆角φ3、角速度ω3、角加速度α3间的数学关系式，以进一步研究λ对曲柄摆动导杆机构的运动性能优劣的影响。

3.1λ与φ3的关系

图2中，曲柄1的角速度为ω1，与机架的夹角为φ1，导杆3的角速度为ω3，与机架的夹角为φ3，则：

ABsinφ1=BCsinφ3

(4)

ABcosφ1+AC=BCcosφ3

(5)

由式(4)、(5)得：

(6)

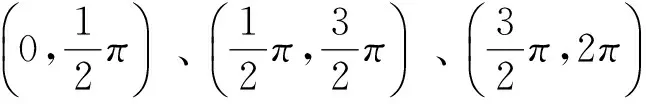
(7)

将式(7)对φ1求导，得：

(8)

因φ1不存在负值，由式(8)有，φ3最大时对应的φ1值为：

(9)

3.2λ与ω3的关系

图2中，

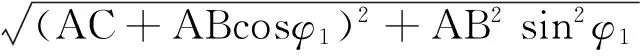
(10)

将式(10)、(4)、(5)联立得：

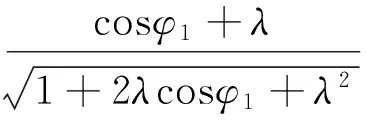
(11)

将式(11)两边对时间求导数，得：

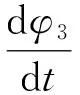
(12)

整理得，

(13)

于是，当φ1=π-arccos(1/λ)时，导杆3的角速度绝对值最小，此时ω3=0。当φ1=π时，导杆3的角速度绝对值最大，即

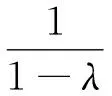
(14)

3.3λ与α3的关系

对式(13)求导，得：

(15)

图4 不同λ时摇杆的运动线图

由图4和表1可知，λ越小，则机构的急回程度越大，而导杆的摆角φ3、角速度ω3、角加速度α3的最大值及其变化率均越大，即运动越不平稳。由上面建立的数学关系式，很容易求得导杆的角位移、角速度、角加速度以及导杆的最大摆角和最大角速度等。

4 结论

(1)分别推导出导杆的角位置φ3、角速度ω3、角加速度α3以及机构的行程速比系数K与λ的关系式，绘制了各自的曲线图，直观地显示出λ对机构的急回特性、运动性能的影响规律。

(3)该项研究建立的数学关系式，使得按给定行程速比系数K设计曲柄摆动导杆机构、分析所设计机构的运动性能变得更加简洁、方便。

[1] 刘善林,王会生.Whitworth急回机构运动特性分析及仿真研究[J].制造业自动化,2007,29(11):83-87.

[2] 邸海燕,张庆功.摆动导杆机构运动特性的解析法研究[J].轻工机械,2009,27(2):56-59.

[3] 何雅槐,唐进元,陈海锋，等.摆动导杆机构键合图建模新方法[J].机械传动,2011,35(10):47-50.

[4] 冯立艳.机械原理[M].北京:机械工业出版社，2012.

[5] 郭卫东.机械原理(第二版)[M].北京:科学出版社，2013.

EffectofλonMotionPerformanceofCrankandOscillatingGuide-barMechanism

FENG Li-yan, HE Shi-wei

(College of Mechanical Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China)

crank and oscillating guide-bar mechanism; motion performance; angular velocity; extreme position angle

The motion performance of the crank and oscillating guide-bar mechanism depends on the characteristic coefficient λ. The value ranges of λ were evaluated when the extreme position angle was acute angle, right angle or obtuse angle respectively. The mathematical relationships between λ and the extreme position angle θ，coefficient of travel velocity ratio K, the guide rod pendulum angle φ3, angular velocity ω3 as well as angular acceleration α3 were established. The value of λ was obtained in terms of the largest value of φ3 and ω3, and then the corresponding curve was drawn. The influence of λ on the motion characteristics of the crank and oscillating guide-bar mechanism was analyzed. An important theoretical basis for the design of the crank and oscillating guide-bar mechanism is provided.

2095-2716(2017)04-0047-05

2017-06-15

2017-09-26

教育部在线研究基金项目(2016YB117)；河北省高等教育教学改革研究与实践项目(2015GJJG084)。

TH112

A