基于能量法的基桩变形P-Δ效应模拟分析

2020-06-03杨明辉李勇智罗宏

湖南大学学报（自然科学版） 2020年5期

杨明辉，李勇智，罗宏

（湖南大学岩土工程研究所，湖南长沙410082）

桩基础是应用最为广泛的基础型式之一，其主要功能为承受竖向荷载，但不少实际工程中，基桩还将承受水平方向荷载，如波浪力、边坡土体推力等，因此轴、横向荷载共同作用下的基桩受力分析也日益得到重视[1-5].对轴、横向荷载共同作用桩基的受力计算，工程中常采用简化分析方法，即先将竖向与横向荷载分开计算，而后再按小变形迭加原理计算桩身内力和位移.但越来越多的研究表明，二者相互影响，不仅水平荷载将使桩身产生较大的弯矩和挠曲变形，而且竖向荷载也会由于桩身挠曲变形而产生附加弯矩，即产生所谓的P-Δ效应[4-7].因此，如何合理考虑该效应已成为复杂荷载下基桩受力分析的关键问题.

近年来，已有大量国内外学者对该问题进行了深入分析.根据对桩-土相互作用分析方法的不同，主要可分为2类.第1类为Winkler地基模型.如赵明华[4]采用m法导得了考虑桩身自重和桩侧阻力时倾斜受荷柔性桩的幂级数解；Zhang等[8]推导了考虑桩周土体屈服的轴、横向荷载共同作用高桩的弹塑性解答方法；Zhu等[9]基于传递矩阵法和Laplace变换推导了轴、横向荷载同时作用单桩响应的统一解答方法，该方法适用于任何形式桩土相互作用弹簧模型；Zhang等[10]分别采用水平弹簧和竖向弹簧来模拟桩-土相互作用，并考虑桩周土体屈服，导得了轴、横向荷载同时作用单桩响应的半解析解.另一类为弹性连续体模型，即将土体视为均匀连续线弹性介质.如Liang等[11]和Zhang等[12]在均质弹性半无限空间中引用Mindlin基本方程，提出了轴、横向荷载共同作用单桩内力位移的边界有限元解法.随后，Liang等[13]在此基础上，采用最小势能原理和变分方法分析了轴向荷载对单桩水平响应的影响，并指出轴向荷载对基桩内力变形的影响与横向荷载水平及桩的长径比有关.

上述方法中，Winkler地基模型无法考虑土体连续性以及桩土之间复杂的三维相互作用，而弹性连续体模型虽然能较好地考虑土体连续性，但其求解过程过于复杂，求解耗时，需基于数值解析才能得到解答，不便于实际工程应用.基于此，本文充分考虑桩周土体连续性、桩-土三维相互作用以及P-Δ效应，引入能量法，基于最小势能原理导得倾斜偏心荷载作用单桩桩身响应的半解析解，并开展室内小模型试验进行验证与对比分析.最后，对影响组合荷载作用下基桩P-Δ效应的主要因素进行了探讨.

1 计算模型分析

1.1 问题描述

如图1（a）所示，基桩桩顶承受水平荷载Q0、竖向荷载P0和力偶M0.桩身总长度为L，直径为2R，桩顶自由段长度为L0.桩周土体为分为n层，每层土的厚度为Hi-Hi-1，其中H0=0，Hn=∞.桩身抗弯刚度为EpIp.在实际工程中，为了保证稳定的受力状态，基桩承受的荷载水平大都较低，桩周土体为小变形情况，接近于弹性受力状态，因此为了简化计算，本文假定桩周各层土体为弹性各向同性的连续介质，其弹性模量和泊松比分别为 Es，i，μs，i.桩土体系采用柱坐标系，如图1（b）所示.此外，假定受荷过程中桩土界面接触紧密，桩和桩周土体无相对滑动和分离.

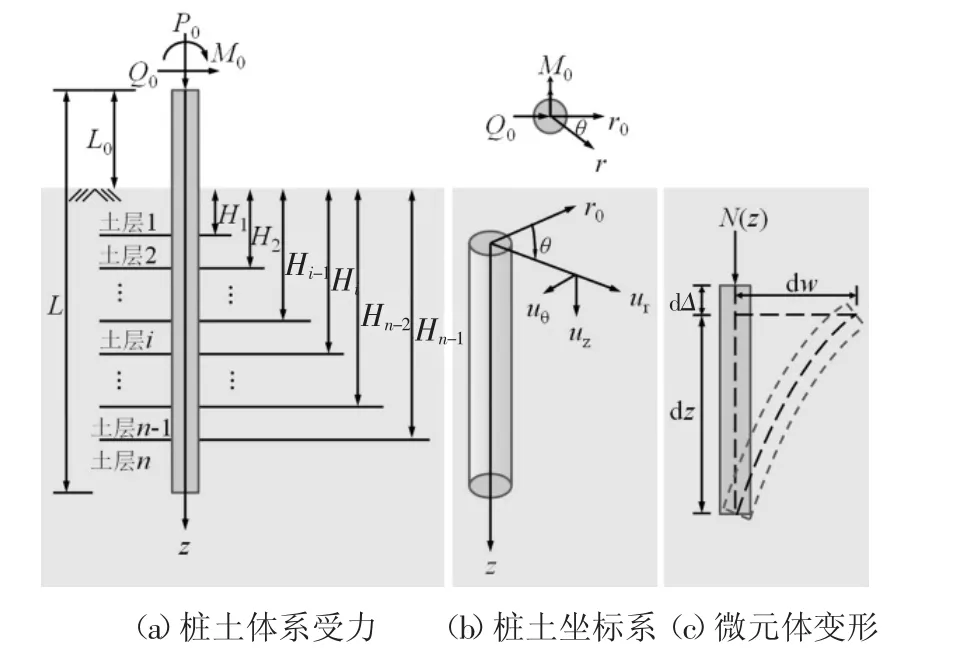
图1 桩土体系平面示意图Fig.1 Schematic diagram of pile-soil system

1.2 土体位移模式

基桩在桩顶荷载作用下发生位移，进而导致桩周土体变形.由于桩土相互作用的复杂性，桩周土体的位移形式也较为复杂.若能建立桩周土体位移和桩身位移之间的函数关系，那么问题将得到明显简化.为此，已有许多学者做了相关研究.Seo[14]在分析成层地基轴向受荷单桩时，提出了如下土体位移模式：

式中：uz表示桩周土体竖向位移；w（z）表示桩身竖向位移；φ（r）表示桩周土体位移沿径向的衰减函数.在此基础上，Seo推导了桩身位移和内力的解析解，并通过与原型试验、有限元等方法对比，验证了该位移模式的合理性.此外，Basu（2009）[15]在文献[16]基础上提出了水平受荷单桩桩周土体的位移模式：

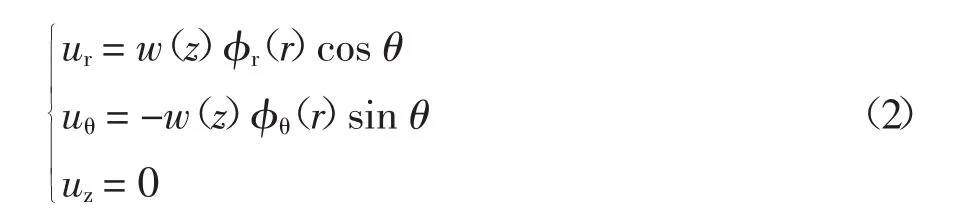
式中：ur和uθ分别表示桩周土体沿径向和切向的水平位移；w（z）表示桩身水平位移；φr（r）和φθ（r）分别表示桩周土体沿径向和切向的位移衰减函数.在此基础上，Basu进一步推导出成层地基中水平受荷单桩桩身内力与位移的半解析解.而本文研究的倾斜偏心受荷基桩中，桩土体系既有水平位移，也有竖向位移，二者均不能忽略.因此，结合式（1）和式（2），本文提出倾斜偏心荷载作用基桩桩周土体的位移模式：

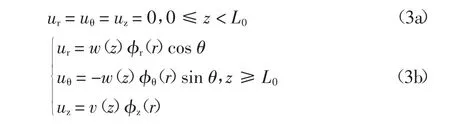
式中：ur、uθ和uz分别表示桩周土体沿径向、切向和竖向的位移.w（z）和v（z）分别表示桩身水平位移和竖向位移.φr、φθ和φz是描述桩周土体位移的无量纲衰减函数，满足边界条件：φr（r=R）=1，φr（r=∞）=0；φθ（r=R）=1，φθ（r=∞）=0；φz（r=R）=1，φz（r=∞）=0.φr（r）和φθ（r）描述了桩周土体水平向位移的衰减，而φz（r）则描述了桩周土体竖向位移的衰减.需要说明的是，上述位移模式忽略了水平位移和竖向位移的相互影响，即认为桩周土体水平位移和竖向位移可以分开计算.此外，基桩受组合荷载作用时，横截面上各点位移分布是不均匀的，为了使问题简化，以基桩中性轴处位移近似代替该截面位移.

1.3 桩土体系能量方程

由上述土体位移模式，可得到土体应变：

根据弹性力学理论，引入虚土桩法，可得桩土体系总势能方程：

式中：第1项和第2项为桩身弹性变形能；第3项和第4项为土体抗力做功产生的势能，其中应力张量σkl可由应变张量εkl通过胡克定律求得；最后3项表示系统外荷载做功产生的势能.而其中第5项，如图1（c）所示，当桩身发生挠曲时，桩顶自由端将产生向下的变位Δ，向下的轴向荷载会做正功，导致系统势能减少.而Δ值等于桩身挠曲线长与弦长之差，即在小变形的前提下，忽略高阶微分，dΔ=w′2dz/2，则轴向荷载所做的功可以表示为：可见，该项考虑了轴向荷载对桩身挠曲变形的影响，进而可合理解释轴向荷载所产生的P-Δ效应.

1.4 桩身水平位移分析

桩土体系势能是一个含有w（z）、v（z）、φr（r）、φθ（r）和φz（r）这5个未知函数的泛函数，由最小势能原理，该泛函的变分应等于0.对Π中与w有关的项进行变分，则可得桩身水平位移w的微分控制方程：

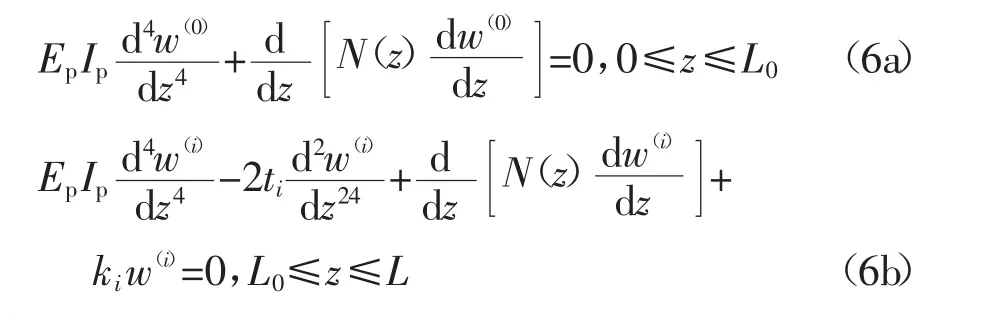
其中

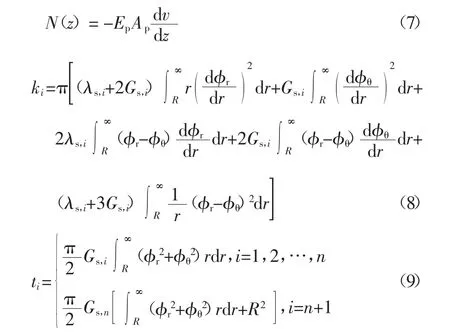
式中：w（0）为自由段桩身的水平位移；w（i）为第 i层土中桩段的水平位移；λs，i和 Gs，i分别为土体拉梅常数和剪切模量.可以看到，方程（6）含有与竖向位移v（z）相关的项，且其系数ki和ti又与φr（r）、φθ（r）有关，其求解较为困难.而Zhu[9]的研究已表明，桩身轴力分布形式对轴、横向荷载共同作用基桩内力和位移影响较小，可忽略不计.因此，为了便于求解上述方程，假定桩身轴力N（z）沿深度线性分布，即：

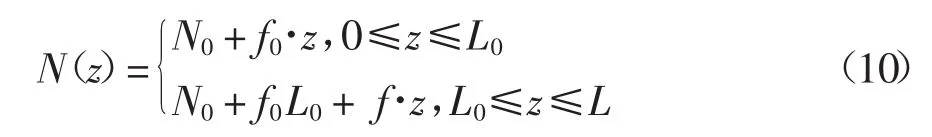
式中：f0= γAp；f= γAp- τu/2；γ 为桩身重度；Ap为桩截面面积；u为桩截面周长；τ为桩周土体极限侧阻力.基于式（10），式（6）可化简为：

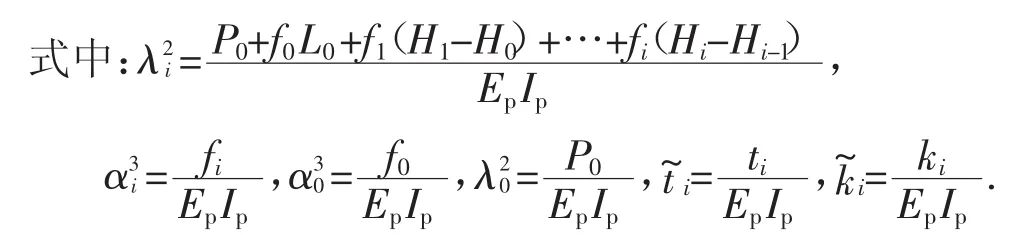
易知，上式满足边界条件：z=0时，

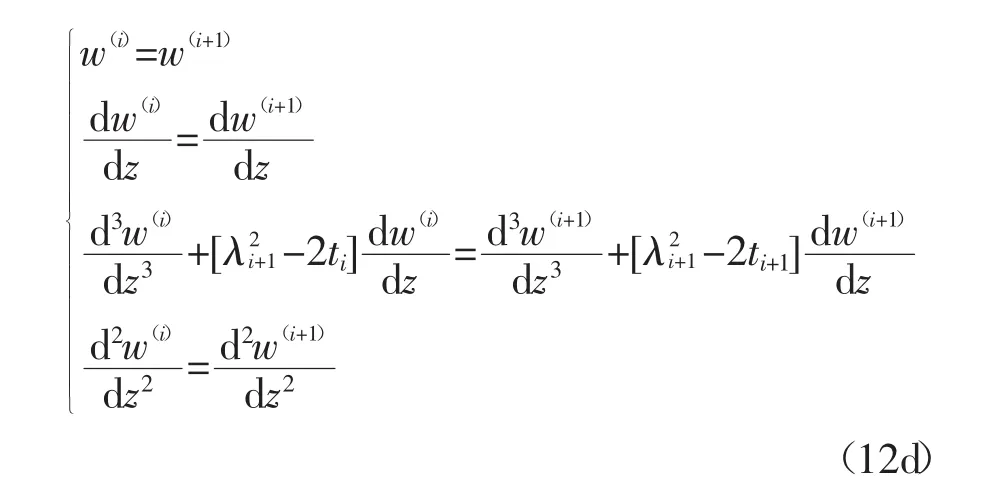
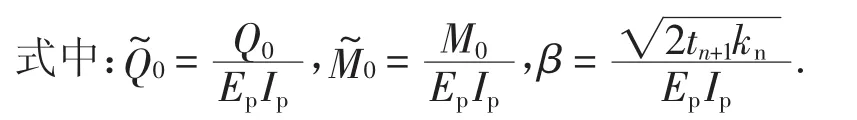
1.5 土体位移衰减函数分析

对Π中与φr（r）有关的项进行变分，则可得到φr（r）的微分控制方程：

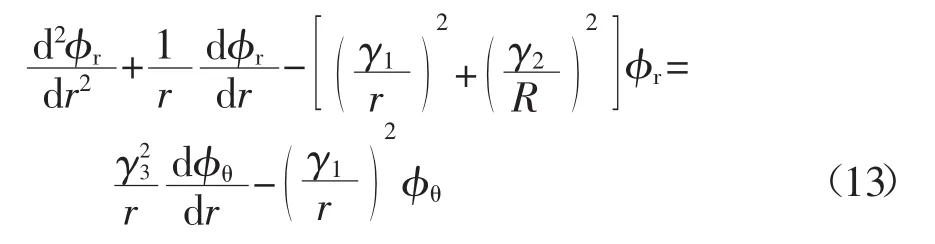
式中：

同理，可得φθ（r）的微分控制方程：

2 控制方程的求解

2.1 桩身水平位移的求解

桩身水平位移控制方程（11a）和（11b）式均为四阶线性变系数齐次微分方程，难以直接获得解析解，本文采用中心差分法求解.桩身差分网格划分如图2所示.将自由段桩划分为N0段，每段长度h0=L0/N0，在桩顶以上和地面下分别取虚拟点-2，-1，N0+1，N0+2.将地面下各土层中的桩段划分为Ni段，每段长度为 hi=（Hi-Hi-1）/Ni，在每段桩的上下取虚拟点-2，-1，Ni+1，Ni+2.则式（11）可以化为：

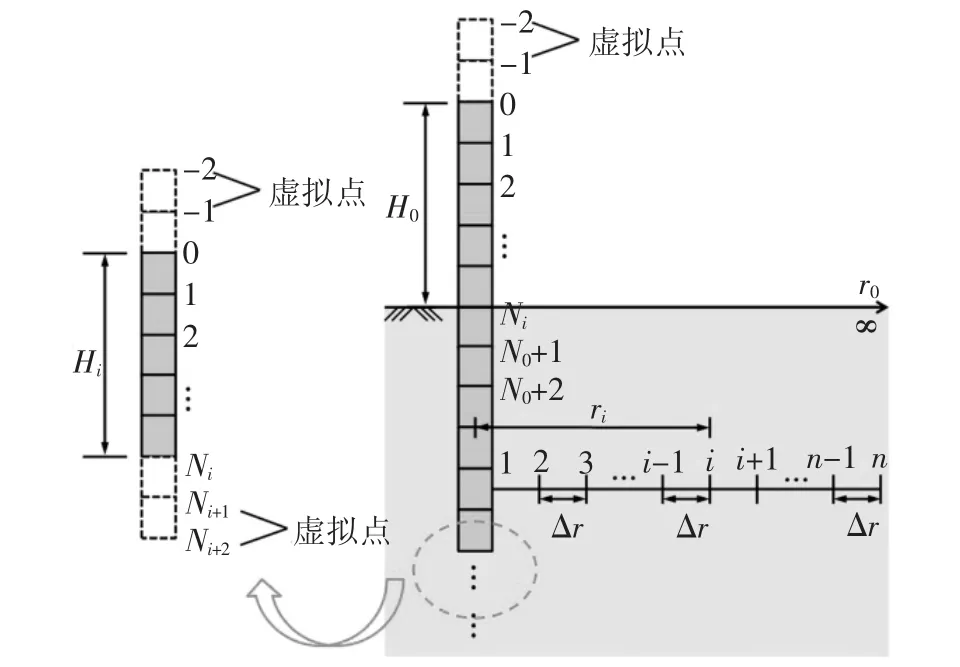
图2 桩及桩周土体的差分网格Fig.2 Difference grid of pile and soil

由式（15）形成的方程组，经边界条件式（16）修正后，即可求解桩身水平位移w（z）.由于篇幅限制，此处仅给出了桩顶自由、桩端固支时的差分解法，其他边界条件亦可按照上述方法求解.

2.2 土体水平位移衰减函数的求解

土体水平位移衰减函数φr（r）和φθ（r）由式（13）（14）控制，同样其解析解不易求，故仍采用有限差分进行求解.而由于式（13）和式（14）相互关联，必须同时求解，因此采用了迭代算法.桩周土体网格划分如图2所示，则式（13）和（14）可以化为：

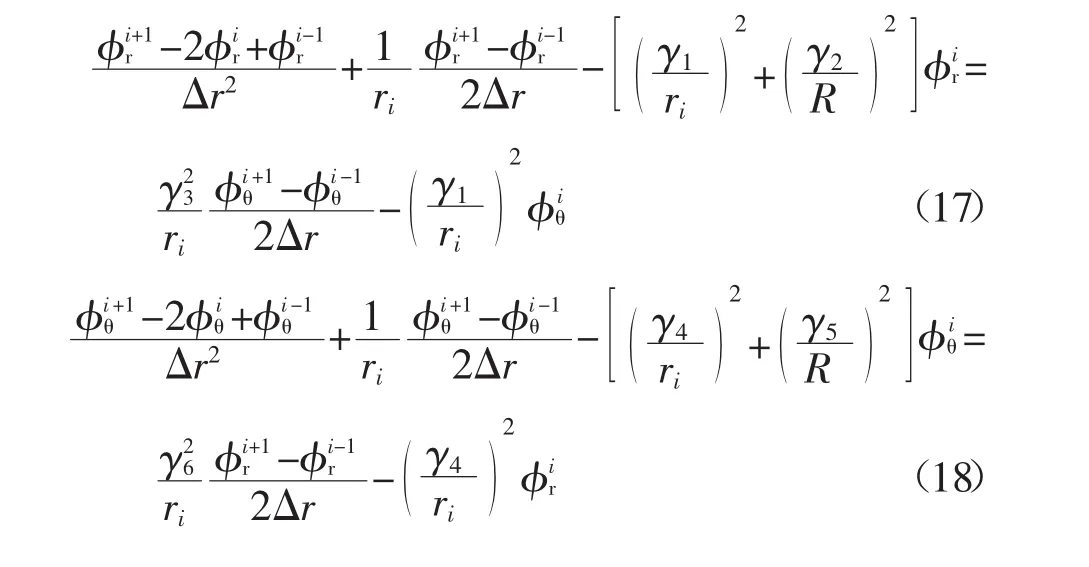
由式（17）和式（18）形成的方程组，再加上前述φr（r）和φθ（r）边界条件，采用迭代计算法即可求解φr和 φθ.对于 φr和 φθ具体的求解过程，Basu[15]已作了极为详细的说明，此处不再赘述.

2.3 算法步骤

为了求解桩身水平位移w（z），必须知道土体参数ki和ti，这些参数与未知函数φr和φθ有关；而要求解 φr和 φθ，其系数 γ1～ γ6又与 w（z）有关.因此，为了同时求解 w（z）、φr和 φθ，必须采用迭代的算法.具体求解过程如下：

1）假定 γ1～ γ6的初始值，例如都取 1；

2）由 γ1～ γ6的值求得 φr和 φθ的值;

3）由 r和 θ的值计算 ki、ti的值；

4）由 ki、ti的值计算得到 w（z）的值；

5）根据求得的 w（z）的值，重新计算 γ1～γ6的值，并记为重复上述计算过程，直到

6）最后一次迭代得到的w（z）值即为桩身各节点的水平位移值.根据上述求解过程，本文基于MATLAB编制了计算程序.

3 方法验证

与现场试验相比，小比例模型试验更容易把握与控制各主要影响因素及条件，因此在机理分析问题上已被众多学者采用并证明了其有效性[17].鉴于此，本文以小比例室内模型试验来探讨倾斜偏心荷载下桩基的受力性能.目前国内外对倾斜荷载下桩基受力性能试验研究主要针对于砂土地基单一地基，而对黏性土环境中或多层地基研究相对较少.为了进一步研究倾斜偏心荷载下单桩受力性能，参考Meyerhof[1-3]等人的小比例试验模拟方法及主要参数选取原则，本次试验分别采用黏土及砂性土模拟上覆软弱地基及下卧优良持力层，选用木桩模拟实际桩体.经过室内土工试验测量，可得桩和土体的相关参数如表1和表2所示.图3和图4分别为本次模型试验加载示意图和模型试验照片.为了消除试验箱中桩-桩之间的相互影响，将桩与桩之间的最小距离设为400 mm，即约为13倍的桩径，根据文献[18]基桩的最大影响范围为8倍桩径的结论，本试验可忽略桩与桩之间相互影响.

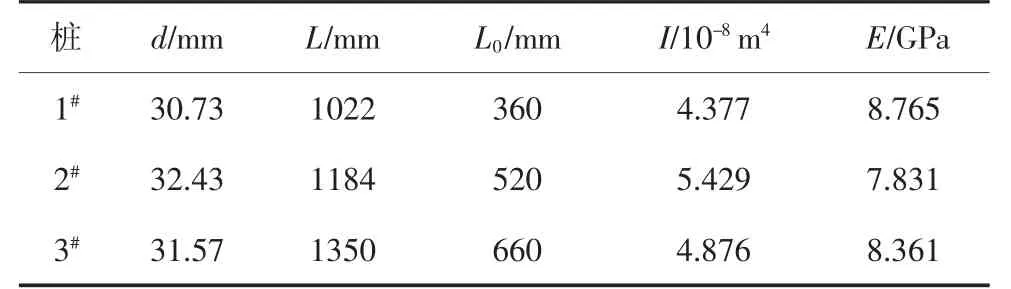
表1 桩的相关参数Tab.1 Pile parameters

表2 土体相关参数Tab.2 Soil parameters

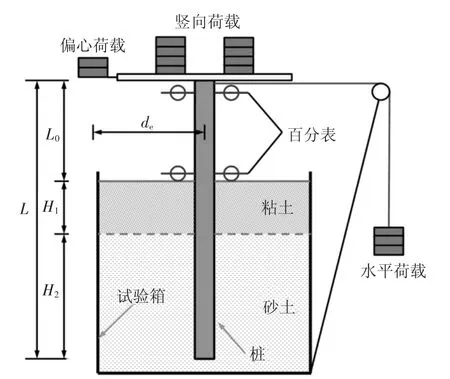
图3 试验加载示意图Fig.3 Schematic diagram of test loading

图4模型试验装置Fig.4 Model test device

图5 为当竖向荷载为757.632 N，偏心弯矩为22.491 N·m时，桩顶及地面处桩身水平位移的变化曲线.由图5可知，本文方法所得结果与模型试验结果较为接近，而由于本文主要考虑土体弹性小变形阶段，因此本文方法结果在加载后期略小于试验结果.同时，图5还给出了本文方法不考虑P-Δ效应时的计算结果，其与试验结果相差较大.图6为当水平荷载为29.4 N时，桩顶及地面处桩身位移的变化曲线.当竖向荷载小于400 N时，本文方法与模型试验结果吻合较好；而当竖向荷载大于400 N时，两者之间差值较大.这是由于当荷载较小时，桩周土体主要表现弹性，此时理论值与实测值较为接近；而随着荷载逐渐增大，上层黏土将表现明显的弹塑性和非线性，并且塑性变形所占的比例越来越大，理论值逐渐小于实测值.但由于实际工程中，基桩承受荷载时大都处于低荷载水平以保证结构的稳定受力状态，因此本文理论解答应用于工程实际是可行的.同时，作为对比，图5和图6也给出了规范推荐方法，即m法的计算结果.以图 5（b）和图 6（a）为例，竖向荷载757.632 N时，本文方法计算的地面处桩身位移与实测值最大相差6.9%，而m法计算结果与实测值最大相差14.6%；水平荷载29.4 N时，本文方法计算的桩顶水平位移与试验实测值最大相差9.6%，而m法计算结果与实测值最大相差19.5%.由此可见，与试验结果相比，m法计算误差约为本文方法计算误差的2倍，因此本文方法在考虑P-Δ效应对桩身受力影响时比m法更加精确合理.

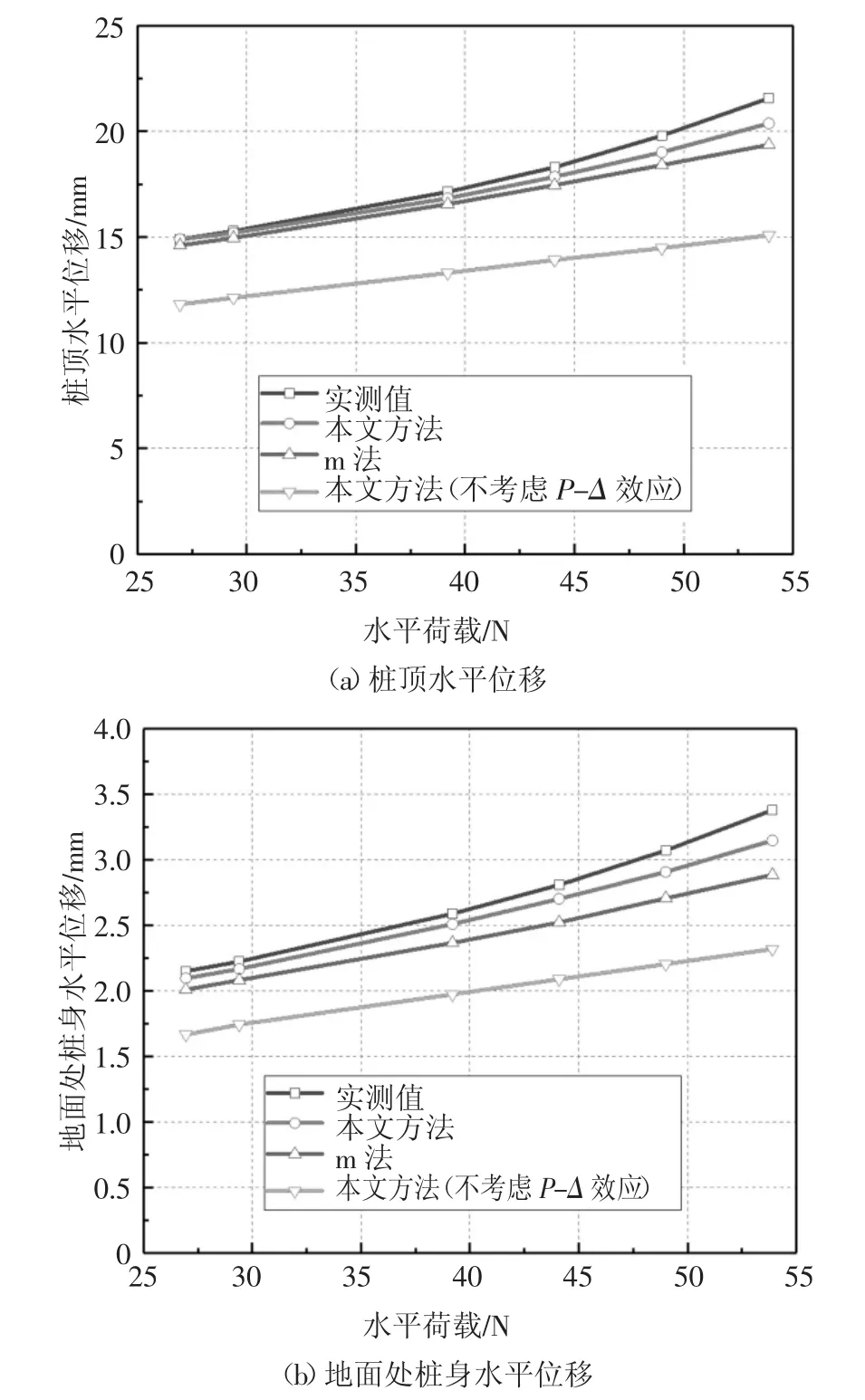
图5 竖向荷载757.632 N，偏心弯矩22.491 N·m时桩的水平荷载-位移曲线Fig.5 Horizontal load-displacement curve of pile under vertical load 757.632 N and bending moment 22.491 N·m

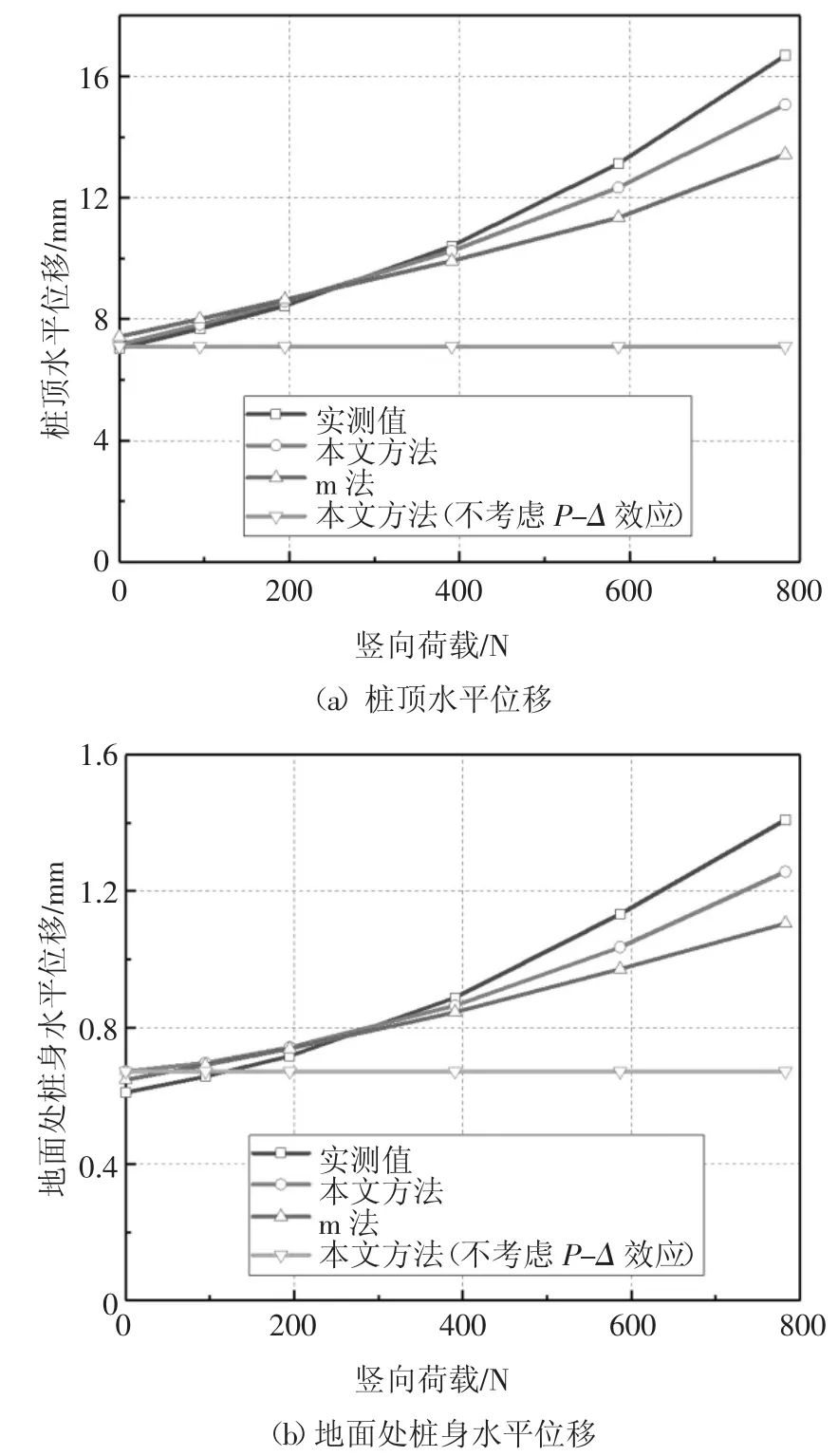
图6 水平荷载为29.4 N时桩的竖向荷载-水平位移曲线Fig.6 Vertical load-horizontal displacement curve of pile under horizontal load 29.4 N

为进一步验证本文方法，下面将本文方法与文献[11]方法进行对比.Liang等[11]引用Mindlin基本方程，提出了轴、横向荷载共同作用单桩内力位移的边界有限元解法，随后采用文献[18]模型试验的数据进行了验证.本文采用与文献[11]相同的参数进行了计算，结果如图7所示.由对比可知，本文方法与文献[11]方法计算结果极为接近.但与文献[11]的边界有限元方法相比，本文计算方法相对更加简单，求解效率更高，便于用于实际工程.

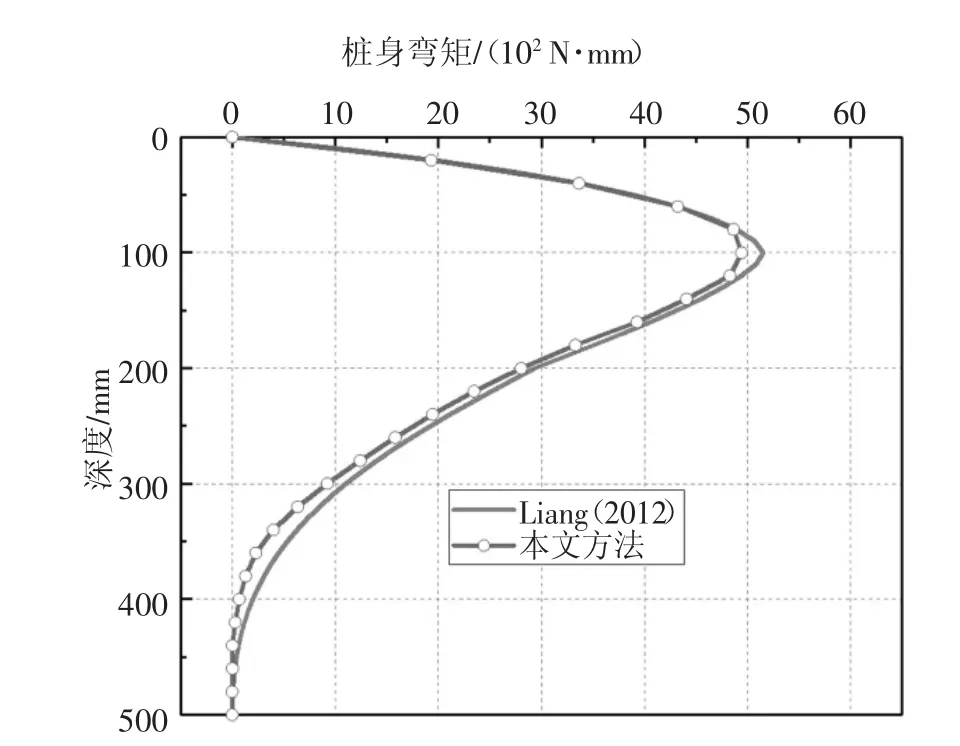
图7 与已有文献理论方法的结果对比Fig.7 Comparison with the results of existing methods

4 参数分析

参考实际工程，在本节的分析中，相关计算参数的取值如下：桩长L=60 m，自由段长度L0=20 m，直径d=1.8 m，桩弹性模量Ep=18 GPa.桩周土体分为2层，上层土体厚度H1=6 m，弹性模量Es1=10 MPa，泊松比μs1=0.3；下层土体弹性模量Es2=20 MPa，泊松比μs2=0.2.桩顶、桩端均自由.Q0=400 kN，P0=4 000 kN，M0=400 kN·m.

4.1 竖向荷载与水平荷载相对大小的影响

图6表明，随着竖向荷载的增加，桩身位移和弯矩都增加，并且竖向荷载越大，其增加速度越快.由此可见，竖向荷载和水平荷载的相对大小对基桩PΔ效应起着至关重要的作用.图8给出了不同竖向荷载和水平荷载下的桩身响应曲线.图9给出了当水平荷载为600 kN时，不同竖向荷载下的桩身水平位移和弯矩.由图分析可知，当水平荷载小于200 kN时，竖向荷载对桩身响应的影响较小，几乎可以忽略不计；而当水平荷载大于400 kN时，竖向荷载的PΔ增大效应较为明显.这是由于当水平荷载较小时，桩身发生的挠曲变形较小，竖向荷载产生的附加弯矩也较小；而当水平荷载较大时，桩身将发生较大的挠曲变形，导致竖向荷载也会产生较大的附加弯矩.此外，图8和图9亦可说明，当竖向荷载与水平荷载的比值小于5时，竖向荷载的P-Δ增大效应并不明显，且在本文的计算假定下，桩身最大位移和最大弯矩与水平荷载近似呈直线关系.而当竖向荷载和水平荷载的比值大于10时，竖向荷载对桩身响应的影响非常显著，并且桩身最大位移和最大弯矩随水平荷载增加而急剧增加.在实际工程中，作用在基桩顶部的竖向荷载通常是远远大于水平荷载的，可见，在进行桩基设计时，考虑竖向荷载的P-Δ增大效应是非常必要的.

图8 不同荷载比下桩身响应随水平荷载的变化曲线Fig.8 Curve of pile response with horizontal load under different load ratio

图9 水平荷载600 kN时桩身位移和弯矩图Fig.9 Diagram of pile displacement and bending moment under horizontal load of 600 kN

4.2 自由段长度L0的影响

自由段长度对桩身的变形起着重要控制作用.为了研究自由段长度的影响，分别考虑了水平荷载Q0=400 kN和Q0=600 kN时，桩身最大位移和最大弯矩随自由段长度变化曲线，同时作为比较，也给出了不考虑P-Δ效应时的情况，计算结果如图10所示.结果表明，随着L0增加，桩身最大位移和最大弯矩都增加，并且L0和Q0的值越大，其增加速度越快.从图10中还可看到，随着L0增加，不考虑P-Δ效应所得的桩身最大位移和最大弯矩的偏差越来越大，表明P-Δ效应对桩身响应的影响更加明显.

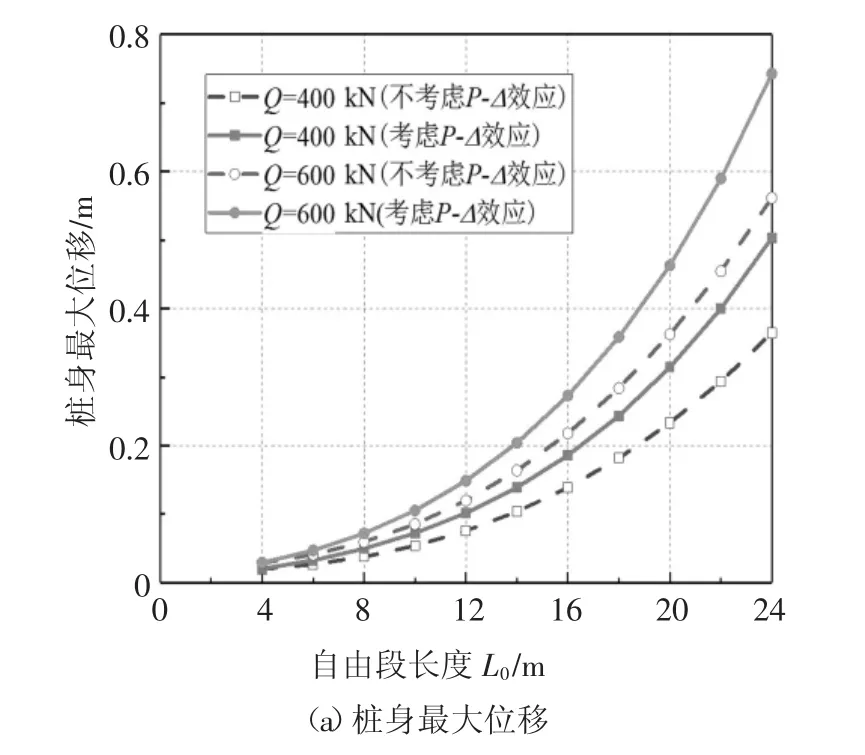
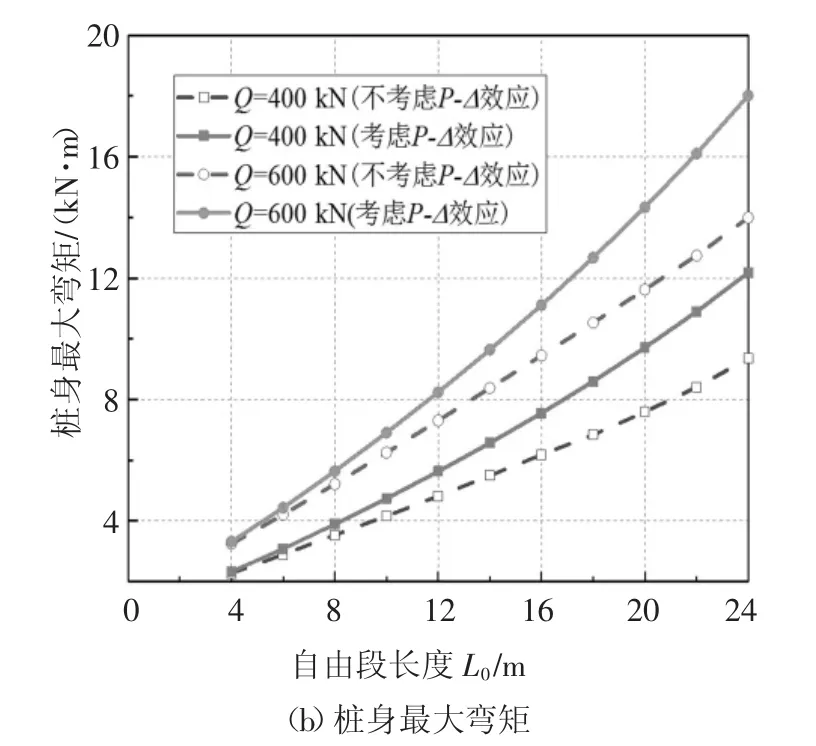
图10 桩身最大位移和弯矩随自由段长度L0的变化曲线Fig.10 Curve of maximum displacement and bending moment with free length L0

图11 桩身最大位移和弯矩随土体弹性模量的变化曲线Fig.11 Curve of maximum displacement and bending moment with elastic modulus of soil

4.3 土体弹性模量和桩身刚度的影响

Zhang[10]和Basu[15]等人的研究表明，倾斜受荷或水平受荷基桩的水平响应主要由桩周浅层土体控制.因此，这里重点研究上层土体弹性模量变化对桩顶位移和桩身最大弯矩的影响.同时，为研究桩身抗弯刚度的影响，考虑了2种不同的桩身抗弯刚度，计算结果如图11所示.由图11分析可知，随着上层土体弹性模量增加，桩顶位移和桩身最大弯矩逐渐减小，且减小幅度越来越小，同时竖向荷载的P-Δ增大效应也逐渐减小.此外，桩身响应受桩身抗弯刚度的影响较大，桩身刚度越大，桩顶位移和桩身最大弯矩越小，竖向荷载的P-Δ增大效应也越小.