基桩超声检测有限元数值模拟研究

戴松仁，李天博，高子俊

（1.江苏大学 电气信息工程学院，江苏 镇江 212013；2.厦门大学嘉庚学院 机电工程系，福建 厦门 363105）

0 引言

随着我国基建事业的发展，高速公路、港口码头、高层建筑等基础设施兴建，基桩得到了广泛应用［1］。按照成型工艺，基桩主要分为预制桩和灌注桩。灌注桩因工序简单、造价便宜、施工方便等优点被大规模采用，尤其是大直径基桩在建筑领域被广泛应用［2］。基桩的建造受地形条件、建造工艺等各种因素的制约，在建造的工程中可能存在空洞、水平间隙、夹泥、缩颈、沉渣等一系列缺陷。这些缺陷会对基桩的强度和耐久度造成安全隐患。因此，在工程实践中对基桩的完整性检测要求越来越高［3］。

基桩检测方法主要有钻芯法、高应变法、低应变法、超声基桩检测法等［4］。与超声检测法相比，钻芯法只能作为一种辅助手段弥补声波测试的盲区；高应变法所需的激荡能量巨大，且代价高昂，一般用来检测基桩的承载力，对于基桩的完整性检测，花费较高；低应变法有其独到的优点，操作简单，但是低应变的冲击波能量较低，应力波衰减十分迅速，对于小型基桩还行，但对于大型基桩，其底部缺陷的应力波较小、敏感性太低，难以满足完整性的检测要求［5］。基桩超声检测法主要对基桩桩身进行预埋声测管，将超声换能器放置于声测管内部，从下往上缓慢拉升，逐点逐步地发射和接受脉冲超声信号，通过分析穿过基桩桩身超声信号的首波声时信号、首波幅值、主频率等声学参数对基桩的完整性进行分析、判断［6-8］。

基桩的超声无损检测成为基桩检测的主流和未来发展方向。基桩超声检测主要判据为首波声时、波幅，辅助判据主要有主频、波形、PSD 等［9］。桩身的缺陷需要综合多种参数进行判断，越多的判据信息越能确定基桩的缺陷。但是这些声学参数受基桩硬化条件、声测管耦合状态、混凝土材料均匀性、测距变化、误读首波等一系列因素干扰，影响着检测结果的准确性［10-11］。

为了更准确地探究声学信号变化和基桩缺陷之间的关系，本文通过COMSOL Multiphysics 软件对基桩进行有限元数值模拟研究。有限元法是工程领域常用的数值计算方法，通过分割和能量原理对工程进行计算。Lysmer 和Drake 于1972 最早提出有限元法并将其运用于地震波的数值模拟，超声波的本质与地震波类似。邵秀民等［12］于1998年讨论了非均匀各项同性介质中地震波的数值模拟方法。对于基桩的数值模拟研究，成联柄［13］通过COMSOL 建立基桩二维模型，张殿群［14］通过ANSYS 建立基桩模型。本文通过COMSOL 建立基桩的三维模型。在基桩缺陷中最具代表性的是空洞缺陷基桩模型和水平间隙缺陷基桩模型，模拟超声波在缺陷和完整基桩内的传播，得到在各类型基桩中传播的声学信号。分析和对比穿过完整桩模型和缺陷桩模型超声信号的首波幅值、声时等声学参数，找出其中的异常点，提出缺陷位置对声压波幅具有很大影响的观点，对于水平间隙缺陷在基桩中难以发现的问题，应对其进行斜侧和PSD 检测。总结相应规律，规避这些影响因素对基桩完整性检测的误判，有助于基桩实际检测。

1 原理分析

超声基桩检测法中，在基桩中传播的超声声波本质为应力波［15］。发射换能器受激励发出超声波，声波在基桩中传播引起基桩内部介质震动，在基桩的内部形成应力波，应力波在基桩内传播，最终被接收换能器接收［16］。

基桩中的混凝土材料主要是由砂、石、水泥、钢筋等组成的一种非均匀介质的复合型材质，内部有大量的非同向界面，超声声波传播过程中的应力波会在各界面发生反射、折射等一系列变化，因此超声波在基桩内的传播过程十分复杂。基于目前研究限制，对于在基桩中传播超声波信号，将基桩模型材料设为各项同性，只研究信号波形首波的波幅、声时、主频等参数，对结果没有影响［17］。因此，将基桩混凝土模型设为各向同性弹性材料，利用软件对超声检测基桩的模拟主要是检测应力波通过低反射在无限均匀基桩混凝土介质中的传播效果。

有限元数值模拟（FEM）是工程领域常用的数值分析方法，主要通过分割和能量原理对工程进行分析。有限元数值模拟主要是将介质离散成三角或矩形网格单元，再选择位移差值函数，将节点的位移分解为网格单元内点的位移、应力和应变，然后建立有限元平衡方程，最后设置边界条件，求解整个平衡方程，得出节点的位移并计算出单元的应力应变等量［18］。

2 平衡方程

将基桩混凝土材料类设为密度均匀的各向同性弹性材料，超声波在基桩中传播时会产生应力，外力作用弹性材料发生弹性形变又叫作弹性应变［19］。各点之间的应变εij和位移量u、v、w之间的关系如下：

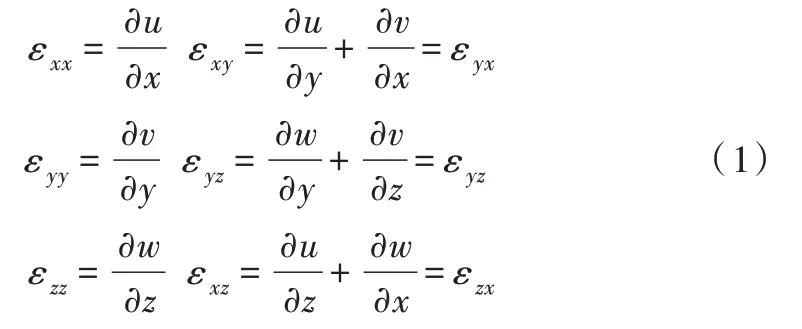
此方程为各点应变和位移关系的柯西方程。其中,εxx、εyy、εzz是x、y、z方向正应变，εxy、εyz、εxz为切应变。

弹性材料中应力εij和应变τij的关系方程为：

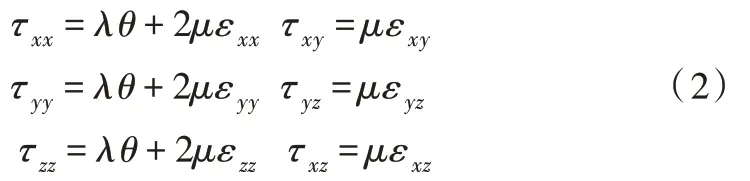
其中，θ=εxx+εyy+εzz（θ）为体应变；τxx、τyy、τzz是x、y、z方向上的正应力τxy、τyz、τxz是切应力；λ、μ是弹性系数。

根据惯性定律表示应力运动的微分方程为：

其中，ρ为密度，Fx、Fy、Fz是x、y、z方向的力，t为时间分量。

方程（3）中未知函数用统一位移表示，将方程（1）、（2）代入，推出弹性波的波动方程：

忽略Fx、Fy、Fz，用矢量表示波动方程为：

3 有限元数值解法

有限元法求解是指将求解空间离散为各子域单元，根据设定的边界相互组合形成结合体，用近似函数表示整个域内要求的未知量，用对应的插值函数表示未知函数的部分特征。将起初待求的无数多自由度的值问题变成求解有限元自由度问题。只要在子域单元内的位移满足稳定性、协调性和完全性要求，有限元的方程即为收敛。建立简单的运动方程，将各单元块组合叠加得到整体运动方程，求解计算运动方程［20-21］。

求解步骤一般为：划分求解子域内的单元节点，构建对应插值函数，通过节点位移和插值位移函数求解任意域内的位移。通过式（5）并利用伽辽金法，结合节点位移变分任意性，推导出系统的运动方程：

其中，A 为质量矩阵，B 为阻尼矩阵，C 为刚度矩阵，R(t)为节点外荷载向量和，a″(t)、a′(t)、a(t)分别是有限元分割体的加速度、速度和位移向量，A、B、C、R(t)分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和节点载荷向量。

将基桩混凝土简化为各向同性弹性材料，去掉阻尼作用的影响，将式（6）简化为：

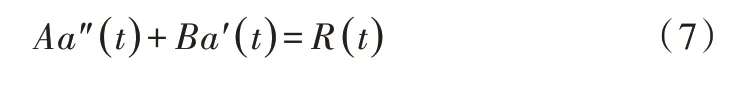
4 仿真模拟

4.1 基桩模型设置

声波在完整基桩中的数值模拟，通过COMSOL Multi⁃physics 建立基桩的三维模型。将基桩混凝土材料参数设为各向同性材料，密度设为2 300kg/m3，泊松比为0.31，杨式模量为30GPa，半径100mm，高150mm，最外层设为完美匹配层，建立如图1 所示三维完整基桩模型。本文彩图扫OSID 码可见。

Fig.1 Three-dimensional model of a complete foundation pile图1 完整基桩三维模型

网格剖分尺寸的选择对于模型计算的精度、耗时、收敛、空间占比都起着绝对性作用。网格尺寸还与声源信号密切相关。研究表明，当单元格尺寸小到一定界限后对精度的影响已经不会很明显。经验显示，只要波长内包含5～9 个空间步长就能满足精度要求。本实验取超声波在基桩中的传播速度为4 000m/s，超声换能器频率为=200kHz。波长为：

因此，本文最大网格设为4mm。

4.2 声波传播特性验证

模拟200kHz 超声波在基桩内传播，选取超声换能器中心为接收换能器接收点。波形如图2 所示，点A 距离发射点为30mm，点B 距离发射点50mm，点C 距离中心发射点80mm，声波起始难以捕捉，对于声时主要是通过首波声时差读取，此时A 点时刻为1.80×10-5S，B 点时刻为2.31×10-5S，C 点时刻为3.06×10-5S，则有V1=4 127m/s，V2=4 054m/s。纵波在无限大固体介质中的传播速度为：

其中，E 为杨式模量，v为泊松比，ρ为基桩密度。将先前设定好的数据代入公式得到Vs=4 252m/s，两者相差不大，因此可以得出COMSOL 模拟超声波在基桩中传播是可行的。

Fig.2 Waveform diagram of points A，B and C图2 A、B、C 点

4.3 模拟缺陷基桩

模拟超声波在具有缺陷基桩内的波形变化情况，当基桩存在缺陷时，缺陷和超声换能器的相对位置是否对超声信号有所影响。这次模拟实验主要探究基桩空洞缺陷和超声换能器的相对位置对超声波信号波形的影响。选取空洞主要是因为空洞缺陷在基桩缺陷中最常见且最具有代表性，并且较为容易建模。

选择声源为正弦波，建立基桩模型，最大网格设为5mm。由于加入了基桩换能器陶瓷振子模型，将最小网格设为0.003 1mm。图3 为完整桩模型，图4 为模拟超声换能器的氧化锆陶瓷，模型半径为10mm，高为5mm。其主要作用为超声波在基桩中传播所产生的应力。

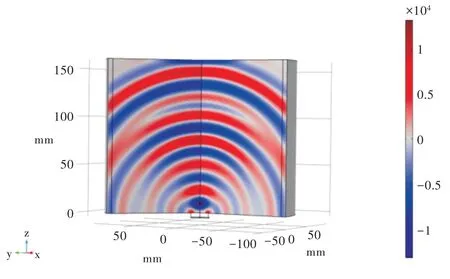
Fig.3 Non-defective pile model图3 无缺陷桩模型

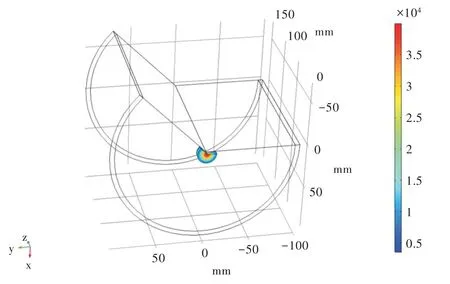
Fig.4 Simulated ultrasonic transducer图4 模拟超声换能器

将D（0，0，0）设为采样点模拟超声波发射换能器，E（0，0，150）设为采样点模拟超声接收换能器。分别在（0，0，20）、（0，0，30）、（0，0，40）、（0，0，50）、（0，0，60）、（0，0，70）、（0，0，80）（0，0，90）、（0，0，100）、（0，0，110）、（0，0，120）、（0，0，130）点处设置空洞缺陷，根据超声检测的灵敏度不大于波长的理论，本实验采用200kHz 超声信号，20mm 波长，因此设立接近极限的缺陷直径为22mm 的球体空洞缺陷（见图5），探究极限情况下缺陷位置和超声换能器位置的相对变化对接收到的超声信号的影响。缺陷处波形比较如图6 所示，首波幅值、声时比较如图7 所示。

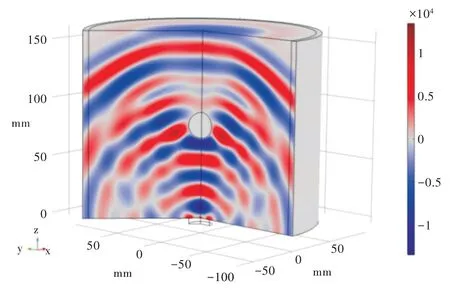
Fig.5 Simulation of empty and defective piles图5 空洞缺陷桩模拟

Fig.6 Waveform comparison of defects图6 缺陷处波形比较

Fig.7 Comparison of amplitude and sound time of first wave图7 首波幅值、声时比较

当基桩存在缺陷时，由于波形的初始时刻难以读到，而波形信号的首波没有叠加其他波形，因此在对仿真超声信号现阶段只研究首波时间和波幅。可以看出，完整桩模型首波的声压幅值为1 197Pa，随着22mm 空洞缺陷出现并且随着位置的改变，声压幅值变化从155Pa 变化到759Pa，通过图7可以明显看出不存在缺陷首波声时小于存在空洞缺陷时的首波声时。当模型中存在直径为20mm 的空洞缺陷，并且空洞缺陷的位置改变时，虽然声时变化十分微小，但是首波的幅值变化很大，并且空洞缺陷越靠近发射或接收点，首波幅值变化越大，幅值越小。幅值声时变化如表1所示。

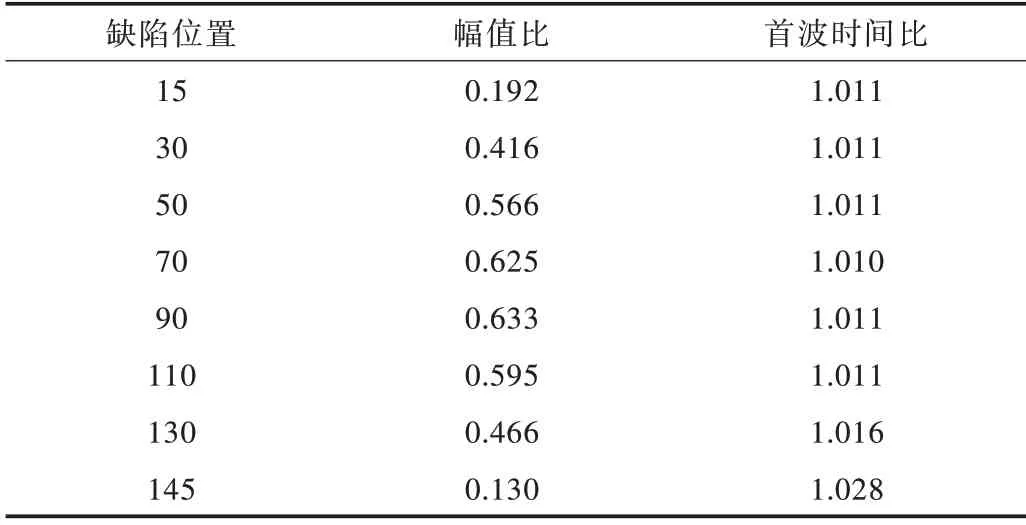
Table 1 Amplitude sound time change表1 幅值声时变化

其中，幅值比为缺陷桩首波幅值和无缺陷桩的比值，首波时间比为缺陷桩首波时间和无缺陷桩首波时间比值。可以看出，缺陷位置越接近超声换能器并且越接近接收换能器，首波波幅变化越大，与波幅变化相比首波时间变化很小。在工程实践中通过幅值判断基桩完整性，不仅需要考虑幅值变化程度，还需确定缺陷位置和超声换能器的相对位置，避免误判。

4.4 水平间隙缺陷及模拟

基桩中的水平间隙缺陷对其完整性的影响巨大，会破坏基桩的受力面积从而对整个基桩造成损伤。将水平间隙缺陷简化为规整的直径，为2mm，将高的范围定为30～70mm，填充材料设为空气。基桩混凝土材料设为各向同性，密度设为2 300，泊松比为0.31，杨式模量为30GPa，将基桩半径设为100mm，高150mm，最大网格设为4mm，建立相应模型（见图8）。

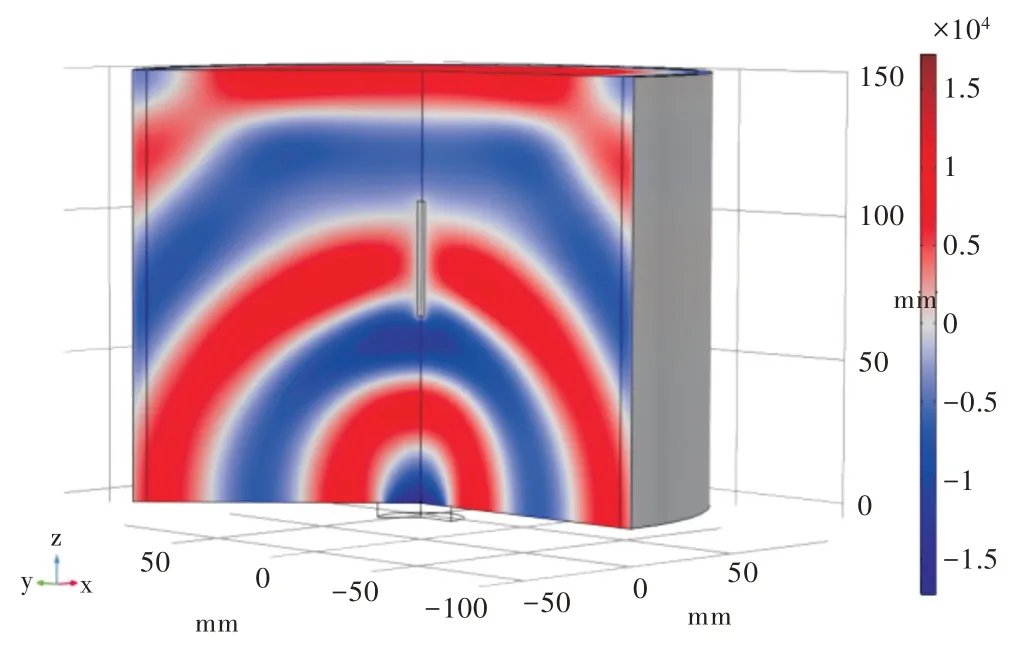
Fig.8 Model of horizontal defect foundation pile图8 水平间隙缺陷基桩模型

将水平间隙缺陷设为圆柱体，填充为空气，底部直径设为4mm，高分别取30mm、50mm、70mm，并且保证高度一直在发出和采集点的中间位置，比较幅值和声时变化如图9 水平缺陷处波形和图10 水平缺陷处首波波形所示，随着水平缺陷的变大，首波声时变化为S，变化很小，从波形图上看几乎无变化，声压变化了12.5%，属于易忽视的微小变化，不容易观察出来。

Fig.9 Waveform comparison of horizontal gap defects图9 缺陷处波形比较

Fig.10 Comparison of first wave waveform at horizontal defect图10 缺陷处首波波形比较

面对此类缺陷，首波声时和首波幅值变化都很小，不易发觉，但此类缺陷对基桩完整性伤害很大，应重视这类基桩缺陷，尽量避免误判漏判。针对这一类缺陷，在一般性基础检测中容易忽略，在基础检测的同时增加扇形扫测和斜侧，找到声学信号异常点，减少误判。

5 结语

在基桩的无损检测方面，超声无损检测凭借其特有优势成为未来发展主流方向。传统超声无损检测受限于检测环境而无法准确全面地对声时信号进行分析，鉴于此，本文提出通过COMSOL 对基桩进行数值仿真，对缺陷和声时信号进行分析，研究声学参数和基桩缺陷之间的相对关系。建立完整基桩模型、具有代表性的空洞缺陷基桩模型和在实际检测中容易被忽略的水平间隙缺陷基桩模型。通过对比完整基桩和空洞缺陷基桩模型得到缺陷随位置变化规律：超声波发射和接收换能器的位置与缺陷的位置对采集到基桩的超声信号有一定影响，主要是对声波信号中的幅值影响较大，换能器位置固定时缺陷位置越靠近检测的超声换能器，对首波幅值影响越大，尤其是靠近接收换能器，幅值衰减巨大，因此在通过幅值对基桩完整性进行判断时还应该对缺陷位置进行定位分析。建立水平间隙缺陷模型，与完整基桩模型声波信号对比，水平间隙缺陷首波声时和幅值均变化很小，在检测过程中不易被发觉，容易被忽略，在工程应用中应当重视这类基桩缺陷，在基础平测的同时增加斜侧和扇形扫描以避免误判漏判。

本文将数值模拟基桩材料设为各项同性弹性材料，实际完整的基桩材料包括粗骨料、水泥、沙等复合材料，而不仅仅是各项同性材料，因此存在一定误差。后续研究中，在建立三维基桩模型的同时，还应模拟基桩检测所需声测管和超声耦合剂，使模拟结果更加贴近实际。