孕育型土洞地陷判据研究

2020-06-03苏永华周乾蹇宜霖

湖南大学学报（自然科学版） 2020年5期

苏永华，周乾，蹇宜霖

（湖南大学土木工程学院，湖南长沙 410082）

地面塌陷是指土中物质移动导致的地表渐进下陷或者突然坍塌，其表现形式以场陷为主，事故现场塌坑多呈圆锥形、圆柱形、球形塌坑.地面塌陷通常与地下孔洞存在密切关系.

蒋小珍等[1]根据试验提出将发育过程应分成土洞的形成、土洞的扩展、近地表土洞的扩展3个阶段；Ouyang[2]认为地陷过程分为地下水位下降阶段、地层孔洞产生阶段、孔洞扩张阶段、地陷形成阶段；Fehdi等[3]认为在地下水溶蚀作用下，石灰岩会溶解形成空洞，空洞到达一定规模后，上覆土层突然失稳，引发地陷；Sagaseta[4]采用极限分析法研究了无摩擦角的理想土地下球形孔洞的临界覆土厚度；陈国亮等[5]做了“自模拟”的岩溶塌陷土工模型试验，研究表明，土洞顶部的剥落是由里而外缓慢地发展，是一个渐变连续的过程，但当土洞扩展至近地面时，开始产生突发性破坏发生地面塌陷；贺可强等[6]将土洞顶部覆盖层土视为压力拱，以此分析其力学机理，从而确定临界土洞厚度；万志清等[7]推导出基于临界水位降幅、临界地下水流速以及临界抽水涌水量的表达式并分析了土洞的形成机理及土洞发育的影响因素；肖武权[8]通过有限元软件模拟土洞，以塑性区贯通至地表作为地面塌陷的判据，并以此计算临界深度；李涛等[9]采用土体塑形极限平衡理论导出了计算地陷的安全系数公式，提出了基于土层厚度和地陷漏斗最大沉降的地陷预测与评估方法.

上述研究基于二维平面研究地陷机理，由于地表失稳判据如塑性区贯通判据、数值计算收敛判据等具有不确定性，因而其有效性有限.而地陷安全系数公式假定路面塌陷的覆盖层塌落体是圆柱体，现实中软土塌落体形状一般有圆柱体、漏斗体，故本文以突变理论为基础，建立三维数值模型模拟地下孔洞的发育，将孔洞发育的连续过程离散化，通过离散的位移序列拟合得到孔洞发育过程引起的地表沉降过程；根据沉降序列与孔洞半径建立突变模型，推导出地表失稳判据；通过覆盖层土体失稳的一致性、同时性、塑性区判据及工程实例初步验证判据的合理性；基于判据得到地表塌陷范围及覆盖层厚度，并探讨临界孔洞半径对土体各参数的敏感性.

1 城区地表塌陷特征

地表沉降过程是一个缓慢渐变、连续的过程，地表被迫从稳定态转变到新稳定态，以此往复.当孔洞发育至地表塌陷阶段，地表稳定态再次破坏，无法到达另一稳定态时，整个系统失稳彻底破坏，地表剧烈下沉.该类地陷的发生多无明显预兆，位置隐蔽，因此有必要开展土质地层地陷研究，分析地陷产生原因和规律，识别土质类地陷濒危状态.

地下孔洞发育过程中，地表状态从沉降、下陷到突塌，是一个渐变下陷到突变破坏失稳的过程，地表的动力学行为具有多重性，演化路径也具有典型的非线性特征，即分叉行为.该现象在数学上可用一个分叉集来描述，地表状态的突变正是受这些突变集中奇点性质控制的，因此考虑引入突变理论.为此，本文利用突变理论建立三维土洞发育过程地表失稳判定数学模型，进而量化判定过程，并以此获得地表塌陷临界覆盖层厚度及地表塌陷范围.研究成果不仅有利于加深对土质地层地陷机理的了解，而且对城区地陷的预测和防治具有参考价值，能够为工程实践提供参考.

2 地表塌陷的突变分析模型

2.1 地表失稳判据及临界孔洞半径确定

初期孔洞，其覆盖层厚度较厚，孔洞半径较小，由于平衡拱存在，孔洞上方地表处于稳定态.在渗流作用下，洞壁逐渐剥落，使得半径扩大，原稳定态遭到破坏，到达新稳定态，此时覆盖层厚度变薄.由于各种因素对孔洞的影响，系统远离稳定无法达到新稳定态时，地面会给人突然下陷的视觉感，即地面突塌，此时导致地陷时的孔洞半径称之为塌陷半径.地表沉降变形会随孔洞发育而逐渐增大，监测地表失稳敏感点，分析地表濒危状态，以此分析地陷是可行的.因此，本文建立地下孔洞球心竖直对应的地面点A的沉降序列和地下孔洞扩展半径R的数学关系表达式，再将其转变为突变理论中的突变尖点理论模型势函数，通过计算其交叉集值来判断地表稳定状态.

利用FLAC3D的NULL命令，监测模型孔洞半径以0.1 m为间隔离散发育时A点的竖向沉降值，可得到孔洞发育过程中一系列半径下的地表沉降值，将两者拟合为泰勒级数形式的关系曲线.为获得尖点突变势函数的标准形式，将其截取至函数4次项如下：

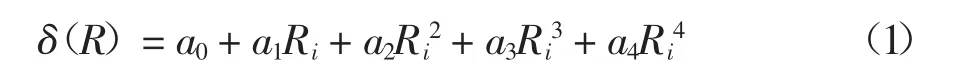
式中：a0、a1、a2、a3、a4为待定常数项；R 为地下孔洞的发育半径.令

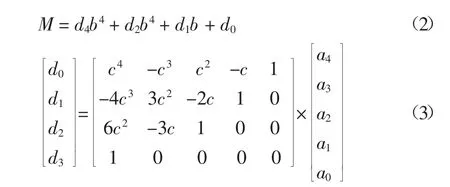
进一步研究式（2），可将其化为

式中：

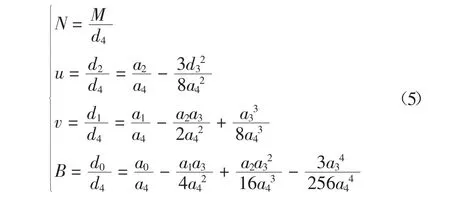
由尖点突变模型知，对式（4）分别求一阶、二阶导数得：

式（6）是突变理论中尖点突变的A3类标准开折，式（6）（7）均与常数项B无关，根据以上各式的推导，孔洞发育极限半径的尖点突变理论标准势函数模型可确定为：

在地下孔洞扩展的过程中，该过程的状态是由控制变量u和v以及状态变量b确定.在由（b，u，v）所构成的三维状态空间中，突变流形即平衡曲面为所有平衡点的集合，平衡点应满足

对于突变点，不仅要满足式（9），还要满足

联合求解方程（9）（10），可得到突变点应服从的控制参数曲面为

图1的突变流形是皱折曲面.在流形上，任何相位点（b，u，v）的b值总是随控制参数u-v连续变化而平滑变化，而控制参数u-v的取值越过曲线8u3+27v2=0时，b值将发生突变，即当相点在曲面边缘上时，它必定回跳到另一叶上.所以，当系统控制变量u和v位于交叉集外区域Δ＞0时，相应的突变流形空间点在流形上叶或下叶会平衡变化，地表稳定；Δ=0时，流形点位于中叶或上叶边缘，即将发生突变，此时系统处于临界状态，也就是极限平衡状态，此时的孔洞半径即临界半径；而Δ＜0时，流形点位于不稳定的中叶，所以系统处于不稳定状态，地面发生塌陷.

图1 尖点突变模型的平衡曲面和分叉集Fig.1 Balance curved surface and bifurcation set of cusp catastrophe model

2.2 地下孔洞发育下地面稳定性判定的实现过程

地下孔洞发育过程中，土体的破坏方式主要是拉破坏与剪破坏.采用FLAC3D中既能考虑剪切破坏又能考虑拉伸破坏的Mohr-Coulomb准则进行计算，比较符合实际情况，且FLAC3D能考虑大变形.其破坏准则的剪切破坏判据为：

拉破坏判据：

其中：

φ是土体内摩擦角，c是黏聚力，σt为抗拉强度.

基于尖点突变模型理论的地下孔洞发育极限半径稳定性判定过程如下：

1）FLAC3D软件建立地下孔洞几何模型并合理划分网格，进行初始地应力平衡.

2）采用Mohr-Coulomb模型，使用FLAC3DNULL 0.1 m，进行弹塑性求解，计算直至收敛，并记录监测点竖向位移；然后向外NULL 0.1 m以模拟地下孔洞发育，再次记录监测点竖向位移；依此类推，记录孔洞发育过程中地面监测点的竖向位移.

3）地下孔洞逐层发育过程中，对记录好的竖向位移和孔洞半径进行泰勒级数拟合，并截断至4次项，得到孔洞发育过程中，地面监测点的竖向位移和孔洞发育半径R的拟合函数δ（Ri）.

4）采用地下孔洞发育过程地面位移变化的尖点突变模型，根据判据确定地下孔洞的极限半径.需要说明的是，本文对地下孔洞的模拟，每次孔洞半径发育长度相等，因此，在计算过程中，只有在确定此半径下，系统稳定，才进行下一次发育，如果下一次发育后系统状态判定为不稳定，则视上一次半径为极限半径.地下孔洞模拟流程见图2.

图2 判定过程流程图Fig.2 Flow chart of determination process

3 骤发型塌陷机制分析

3.1 模型建立

地下孔洞的形状各异，为研究方便，不少学者对地下孔洞进行合理简化[1-2，7-9].本文利用FLAC3D软件建立三维模型，将地下孔洞的形状简化为球形，利用地表失稳判据来分析一定埋深下孔洞发育的极限半径.鉴于宋谷长等[10]统计的北京路面塌陷，其80%发生在深度约5 m内的塌坑，故采取孔洞埋深5 m，模型长30 m，宽15 m，高13 m，共110 000个单元.计算模型的边界条件设置为：设球心坐标（0，0，0），监测点1坐标（0，0，5），模型的两侧均为x方向位移约束，模型底部为水平和竖直方向位移约束，模型顶部为自由边界，模型前后是y方向约束.地下孔洞模型见图3，岩土参数见表1.

图3 计算模型Fig.3 The numerical mode

表1 岩土体物理参数表Tab.1 Mechanical parameters of geotechnical

随着地下孔洞的发育，地表沉降值逐渐增大，其沉降发展趋势如图4（a）所示.

当孔洞半径超过2.0 m时，沉降趋势明显，其下沉趋势越来越大，利用判据计算可定量判定地表稳定性.首先将各监测点之前所有数据点进行泰勒级数拟合，表2为模拟孔洞半径从2.2 m发育到2.35 m的过程判定计算结果.根据地表失稳判据，当孔洞发育到2.3 m时，Δ值大于0，故稳定；当地下孔洞半径发育到2.35 m时，Δ值小于0，地面失稳；那么孔洞发育临界半径处于2.3～2.35 m之间，两者相差不大，基于安全角度考虑，视2.3 m为孔洞极限半径，将2.35 m视为地面失稳的塌陷半径.

孔洞发展到2.35 m时，由图4（b）可知，孔洞上方塑性区已贯通，且地表深色剪切破坏区大致呈现圆形，地表塌陷区的边界是白色拉破坏区，同时孔洞发育过程中，尽管上部地表发生塌陷，但塌陷体内部存在稳定区域.

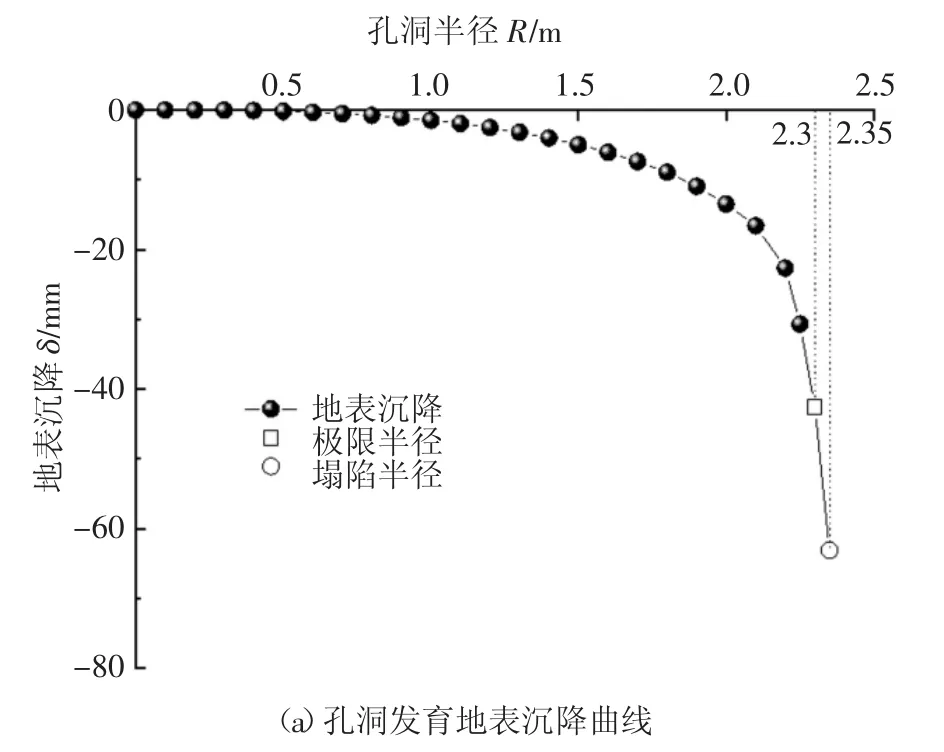
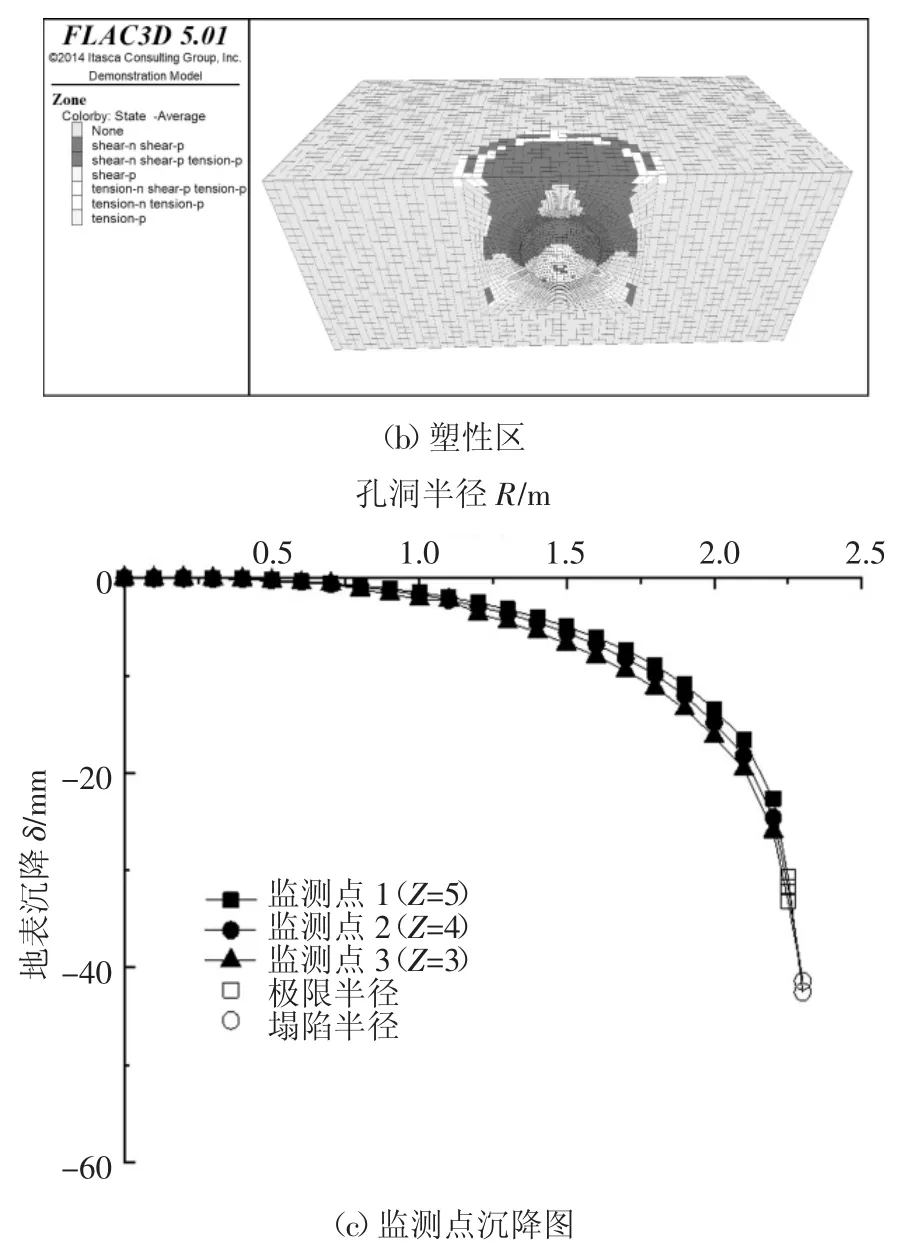
图4 模拟结果Fig.4 The result of simulation

表2 各半径下突变模型控制变量及ΔTab.2 Control variables of cusp catastrophe models and Δ

图 4（c）中，监测点 1 位于模型 3 上表面（0，0，5）处，监测点2、3位于监测点1竖直往下1 m、2 m处，监测内容为竖向位移.通过比较可知，孔洞发育的过程中，三点位移趋势一致，故而上部土体位移趋势一致；表3中，Z表示孔洞球心距离A点的竖向距离.由表3知，球心位置分别位于Z=3、Z=4、Z=5的3种孔洞，其极限半径均为2.3 m，即当孔洞半径为2.35 m时，其Δ均小于0，而孔洞半径为2.3 m时，三者Δ均大于0，因此孔洞上方土体沉降趋势是一致和同时的，所以当地下孔洞半径发育到塌陷半径时，整个上部土体一同塌落，造成地面塌陷.

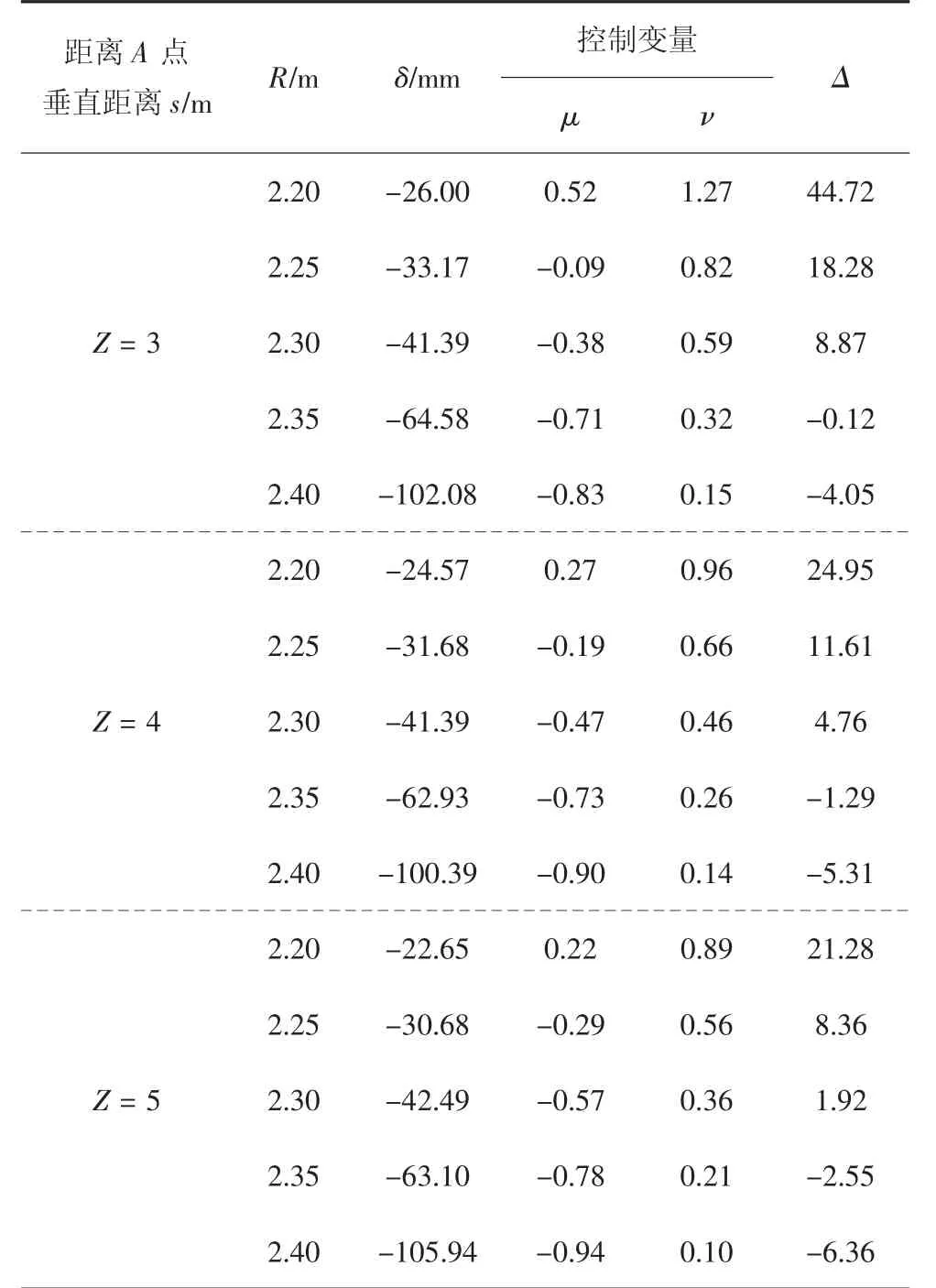
表3 监测点Δ计算结果Tab.3 Calculation results of the monitoring point about Δ

3.2 粘聚力、摩擦角对临界覆盖层厚度的影响律

粘聚力分别为 6 kPa、8 kPa、10 kPa、12 kPa、15 kPa时，其地下孔洞的极限半径分别为1.4 m、1.8 m、2.3m、2.7 m、3.6 m.故其临界覆土厚度分别为3.6 m、3.2m、2.7 m、2.3 m、1.4 m，粘聚力与临界覆盖层厚度的关系如图6（b）所示.

由判据得到的临界覆盖层厚度标注在图5（a）上，从图5（b）可以看出：随着粘聚力降低，地下孔洞临界覆盖层厚度在不断变大，粘聚力越大，土体抗剪强度越高，相同尺寸孔洞上的临界覆土厚度应该越大，这与一般事实相符.两者可以较好地拟合线性函数.

摩擦角分别为 12°、14°、17°、20°、22°时，其地下孔洞的极限半径分别为 1.5 m、1.7 m、1.9 m、2.1 m、2.3 m.故其临界覆盖层厚度分别为3.5 m、3.3 m、3.1 m、2.9 m、2.7 m.内摩擦角与临界覆盖层厚度的关系如图 6（d）所示.

对比粘聚力和内摩擦角与临界覆盖层厚度的两个函数关系式，临界覆盖层厚度显然对粘聚力更敏感.但是土体粘聚力、内摩擦角降低时，临界覆盖层厚度无疑是增大的，所以当孔洞覆盖土体厚度处于临界覆盖层厚度时，土体粘聚力、内摩擦角分别或同时减小，地表会失稳造成塌陷事故.当遇见暴雨天气，土体遇水变软，地表相比平时更容易失稳，覆盖层厚度在原有自重下又新增一部分雨水重量，使地表更加危险.因此部分塌陷发生在降雨过后.

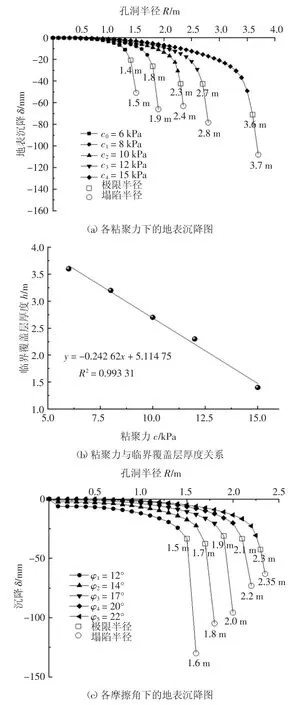
图5 抗剪强度指标与临界覆盖层厚度关系Fig.5 The relationship between the shear strength index and critical soil thickness

3.3 土体弹模、泊松比对临界覆盖层厚度的影响

弹性模量值分别为5 MPa、15 MPa、25 MPa时，其地表沉降曲线图如图6（a）所示.从图上可以看出，弹性模量越大，地表沉降越小，曲线彼此不相交，由地面稳定性判据得到的计算结果表4可知，不同弹性模量的塌陷半径均为2.35 m，临界覆盖层厚度对弹性模量的变化不敏感.在地表沉降图6（a）中，尽管极限半径为2.3 m，对于弹性模量较小的土体，孔洞发育到极限半径时，地表沉降已达到12.7 cm，容易引起警示从而采取措施避免事故.但对于弹性模量较大的土体，孔洞发育到极限半径时，其沉降仅为2.3 cm，此时地表已临近失稳.所以，对于弹性模量较大的土体而言地表易发生突发性塌陷，因为地表失稳前的沉降不易察觉；而弹性模量相对较小的土体，其发生塌陷前地表会发生较大位移变化.因此对于地表沉降失稳判据不应以绝对位移作为地面稳定性与否的判据，不同弹性模量下，地面塌陷前的地表沉降是不一样的，不妨将极限半径下的地表沉降称为安全沉降值，则25 MPa、15 MPa和5 MPa下的安全沉降值分别为2.3 cm、4.3 cm和12.7 cm.而泊松比分别0.2、0.3、0.4时，根据判据的结算结果，其临界覆盖层厚度均为2.7 m，其安全允许沉降变化也不大，分别为4.1 cm、4.2 cm、4.3 cm.所以安全沉降值和临界半径对泊松比的变化并不敏感.

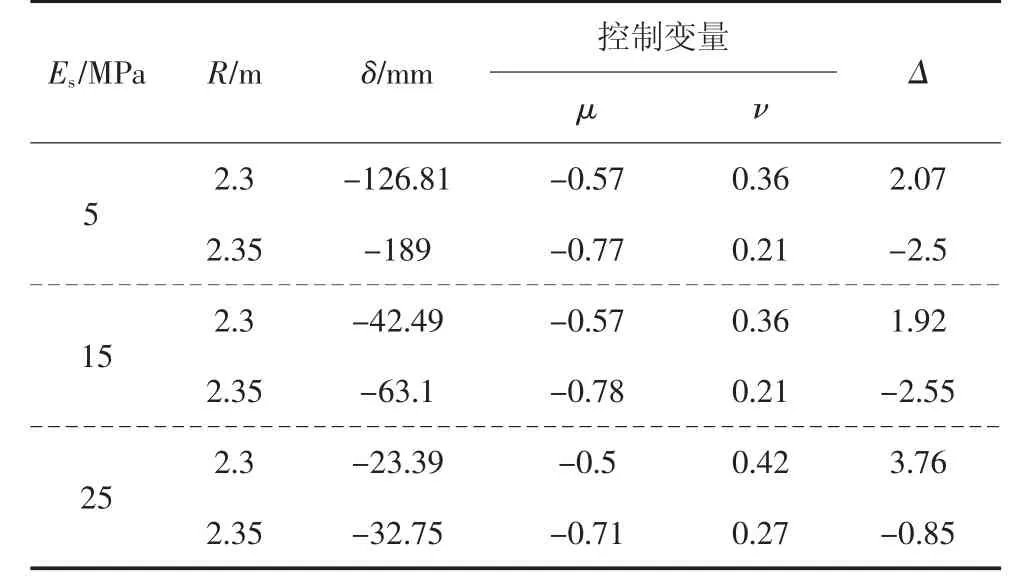
表4 不同弹性模量下的Δ计算结果Tab.4 Calculation results of Δ under different elastic moduli

图6 变形参数下的地表沉降曲线Fig.6 Ground settlement curve under deformation parameters

4 工程实例

4.1 项目背景

珠三角城际轨道交通广佛环线广州南站至白云机场段广佛东环隧道大源站-太和站区间工程位于广州市白云区太和镇.场地地下水主要以第四系孔隙水及基岩裂隙水、岩溶裂隙水为主，地下水丰富.根据钻探揭示了太和站属覆盖型岩溶区，存在隐伏溶洞和土洞，除土洞发育外，还分布大量的冲洪积物，上覆地层多为黏土、粉质黏土、粗砾砂、圆砾土等，由于地下水位较高，第四系地层多受地下水影响，强度较低，易引起地面塌陷，其埋深在2～15 m范围内，项目勘测前期现场发现一处塌坑，塌坑底部为椭球状，半径约2.5 m，坑深约7.6 m，塌区平面范围类似圆形，尺寸约为2.0 m×2.1 m，塌陷周边出现明显的裂缝.由于塌坑临近勘测钻孔区域，其土层由上至下依次为人工填土层，主要为杂填土和素填土，颜色较杂，厚度为1.86 m；可塑状冲洪积黏性土层，呈褐黄色、浅黄色、褐红色等，主要由粉质黏土、黏土组成，含砂粒和粉粒，层厚0.57 m；硬塑状残积-坡积粉质黏土层，呈褐红、褐黄、灰褐色、灰白等色，组织结构已全部破坏，层厚5.82 m；全风化粉砂岩带，呈灰黄色、褐红色，原岩矿物基本风化，层厚12.67 m.由于坑深7.6 m，塌坑底部半径近似为2.5 m，可认为其初期孔洞处于地下5 m左右，并由此逐渐发育从而导致地表突塌，接下来分析此次塌陷.土体参数见表5.

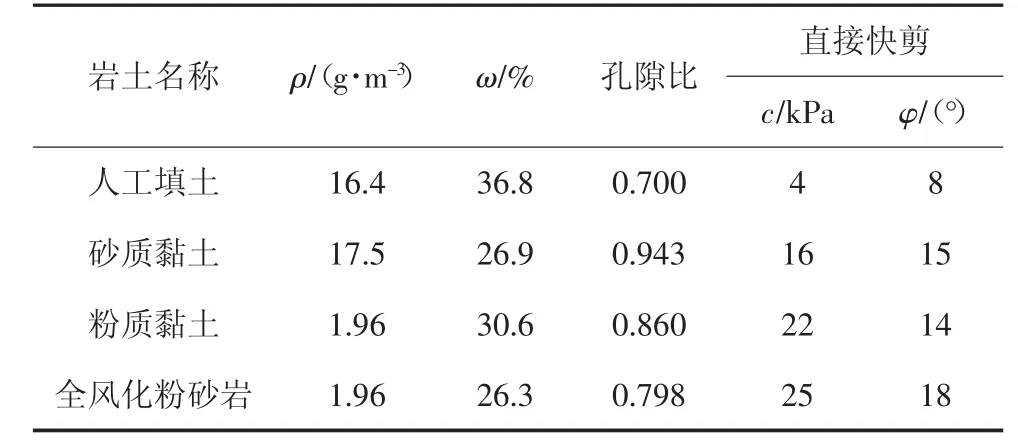
表5 土体参数表Tab.5 The table of soil parameter

4.2 模拟结果及对比

地表沉降如图7所示.地表沉降等值线从A点向外呈圆形分布，且等值线上的数值不断减小.因为地表沉降等值线呈圆形分布，那么地表塌陷范围也应呈圆形分布，即塌陷区是圆形的.

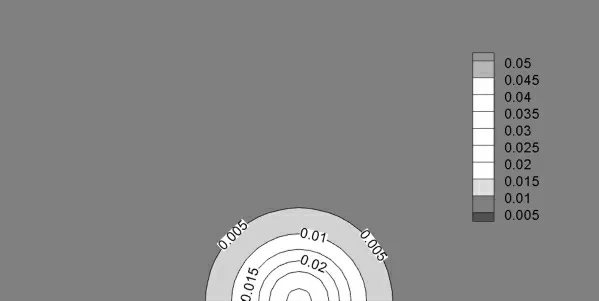
图7 地表沉降图Fig.7 Surface settlement map

根据地表失稳判据，地表塌陷范围的计算结果如表6所示.地表半径为0时即孔洞对应的上方地表点的判别如下.当孔洞半径发育到2.5 m时其判据计算值大于0，此时地表稳定，地表沉降值为3.0 cm；当孔洞半径进一步发育到2.6 m时，地表失稳，其塌陷半径为2.6 m，孔洞极限半径为2.5 m.由于球形孔洞引起的地表沉降呈圆形分布，故可用地表塌陷半径Rc来描述地表塌陷范围.孔洞半径发育至塌陷半径时，临塌边界处的Δ＜0；而孔洞半径发育至临界半径时，Δ＞0.满足这一条件的位置即临塌边界，以Rc为半径，塌陷中心为圆心，可绘出塌陷范围.而通过计算可以得知其地表塌陷区呈明显圆形分布，该圆形塌陷区半径Rc可反映塌陷区范围.计算得到地表塌陷范围半径Rc值为2.0 m＜Rc＜2.5 m.

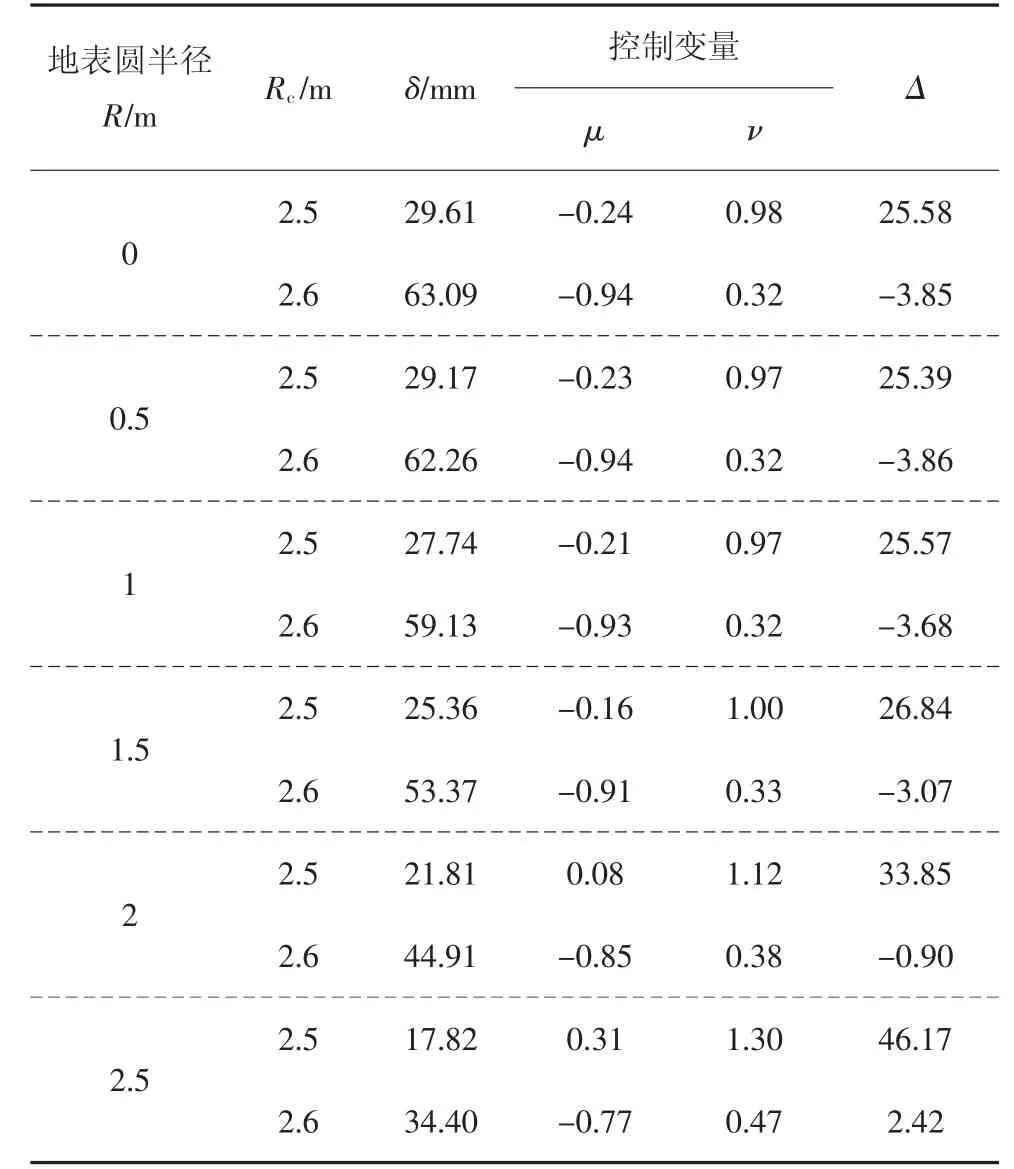
表6 路面塌陷范围Δ计算结果Tab.6 Calculation results of surface area cover the hole about Δ

由塌陷半径时的地表沉降值，可绘制出塌陷后塌坑平面形状.由于交叉集值-0.9相比于2.42更接近0，同时出于安全角度考虑，本文认定塌陷范围半径为2.0 m.数值模拟塌坑深度为球心深度与临界半径之和，其值为7.5 m，而现场塌坑深度为7.6 m；现场塌坑范围为2.0 m×2.1 m，地表塌陷范围模拟为2.0 m，故地表塌陷区范围与塌陷深度与现场情况较为接近；现场底部近球状孔洞尺寸为2.3 m左右，模拟结果显示为2.5 m，数值模拟的孔洞半径比现场塌坑底部的半径大，实际塌陷时由于覆盖层土体掉入坑洞，这会造成现场塌坑孔洞半径比孔洞临界半径小，故模拟结果较好地反应了现场情况.