不同截面形状下弹性支撑多跨梁振动特性分析

2020-06-03鲍四元周静

中国舰船研究 2020年1期

鲍四元，周静

苏州科技大学土木工程学院，江苏苏州 215011

0 引言

梁结构被广泛应用于各种工程，例如建筑、航空航天、船舶领域等。船舶由板和梁构成，在船舶的振动分析中，需要用到梁的振动特性。黄强等[1]将船体简化成了一根两端完全自由、质量和刚度沿长度分布不均匀的变截面梁，并针对其振动时的弹性变形进行了研究。

许多学者都对梁结构的振动问题进行过研究和分析。Abbas[2]使用有限元法对含弹性边界的Timoshenko 梁的自由振动问题进行了求解。Chung[3]综合利用傅里叶级数和拉格朗日乘子，提出了一种在经典边界条件下梁固有频率和模态的计算方法。邹佩等[4]通过拟小波-精细时程积分方法，针对结构离散后将单跨梁振动问题转化为常微分方程组的问题进行了求解。曾文平等[5]提出采用多辛Hamilton 形式分析梁的振动方程，最后运用数值例子说明了理论分析的正确性。王其申等[6]采用差分法对多跨梁差分离散系统固有振动的基本振荡特性予以了推导。刘向尧等[7]建立了3 种常见梁（欧拉梁、瑞利梁和Timoshenko 梁）的自由振动模型，并应用参数变易法进行分析，推导出了自由振动的频率方程。Zhang 等[8]基于有限差分模型建立了Hencky 链杆模型（Hencky Bar-chain Model，HBM）并推导出了HBM 法的频率公式，首次提出采用HBM 法和有限差分法（Finite Difference Mthod，FDM）分析带有内部弹性弹簧的屈曲载荷和振动频率。张振果等[9]采用变量分离结合传递矩阵的方法导出了梁的特征方程，阐述了具有不等跨度、可变横截面以及不连续性任意性梁的几何特征。陈小超等[10]建立了广义函数空间内轴向力作用弹性基础下不连续欧拉梁的振动微分方程，研究了附加质量块的转动惯量对梁—质量块系统的影响。

然而，以上所研究的有关自由振动问题的方法大多具有一定的局限性，例如有些只能作定性研究，有些只能求解特定的边界条件等。Li[11]提出了一种函数的改进傅立叶级数形式，即在传统的傅里叶级数形式中添加4 项正弦函数，该形式的优势在于能够完全消除函数及其各阶导数在端点的不连续问题。周渤等[12]基于改进傅里叶级数方法(IFSM)进行了连续多跨梁结构的振动特性分析。周海军等[13]运用IFSM 方法对轴系的横向振动特性进行了研究。史冬岩等[14]基于IFSM方法，研究了正交各向异性薄板的横向自由振动问题。Bao 等[15-16]基于IFSM 方法，对环扇形板和矩形板的面内自由振动问题予以了研究。

为了研究多跨梁的自由振动问题，本文拟采用一种异于文献[12]的新型IFSM 方法来表示梁位移函数，以避免弹性边界下多跨梁端部不连续的问题。首先，将位移函数代入拉格朗日方程，结合瑞利—里兹方法，将自由振动问题化为标准矩阵特征值形式；然后，利用Mathematica 软件进行编程，求得各阶的频率和振型。

1 含弹性支撑多跨梁振动的计算模型

1.1 几何模型

图1 所示为跨内含弹性支撑多跨梁振动的计算模型图。梁总长度为L，跨数为p。在梁的左、右两端分别设置了横向弹簧和旋转弹簧用来模拟边界条件，并通过设定横向弹簧的刚度系数来模拟中间弹性支撑条件。左端边界的横向弹簧和旋转弹簧分别为k1和K1，右端边界的横向弹簧和旋转弹簧分别为kp+1和Kp+1，从左至右中间弹性支撑的横向弹簧的刚度系数分别为k2，k3，…，kp。当边界条件为固支边界时，需将横向弹簧和旋转弹簧的刚度值同时设为无穷大（例如，取1014EI，其中EI为截面的弯曲刚度）；当边界条件为自由边界时，将横向弹簧和旋转弹簧的刚度值取0 即可；当横向弹簧和旋转弹簧的刚度系数取有限值时，即可模拟弹性约束边界条件。

图 1 含弹性支撑的多跨梁模型Fig. 1 Multi-span beam model with elastic supports

1.2 位移函数的表示

对于含弹性支撑的梁结构，因为梁的振动方程为四阶微分方程，所以采用传统傅里叶级数表示的位移函数在边界处会出现不连续的问题。为了消除梁端各力学变量的不连续性，文献[12]基于无穷项余弦函数叠加4 项正弦函数，采用改进傅里叶级数来表示弯曲位移函数。

不同于文献[12]，本文将采用无穷项正弦函数叠加4 项余弦函数的形式，即适用于任意弹性支撑条件梁挠度的新型改进傅里叶级数为

式中：x∈[0,L]；an为待定常数； λn=nπ/L。

式（1）可称为改进的傅里叶正弦级数，现有的文献在改进傅里叶正弦级数方面研究较少。文献[11]指出，用傅里叶正弦级数或傅里叶余弦级数展开位移函数时均收敛，故本文基于改进傅里叶正弦级数来研究多跨梁的振动问题。

对于图1 所示含有p段的多跨梁，一般应将各段梁挠度假设成不同的挠度函数[7-9,12-13]，但为简便起见，本文采用适合于整段梁的挠度函数。经分析可知，当采用式（1）时，中间弹性支撑处的位移和转角都是连续的；且当中间弹性支撑两侧的刚度EI相同时，弯矩和剪力也是连续的。

在物理意义上，由于横向弹簧的存在会导致中间弹性支撑处的梁剪力出现不连续的情况，因此本文模型引入了整段梁的弯曲位移函数w（x），而未采用分段函数，这是一种近似处理。如果w（x）在整段梁上处处连续，则其一阶导数（对应于截面转角）和二阶导数（对应于截面弯矩）均能在整段梁上处处连续，这与实际情况是一致的。实际上，模型中w（x）的三阶导数（对应于截面剪力）也是处处连续的，但中间弹性支撑处的梁剪力有突变，这种与实际情况不一致所导致的频率值误差较小。后文的算例结果也能反映出，采用适合整段梁的挠度函数能够较好地求解多跨梁的自由振动问题。

对于图1 所示的弹性支撑多跨梁结构，存在如下3 部分势能：

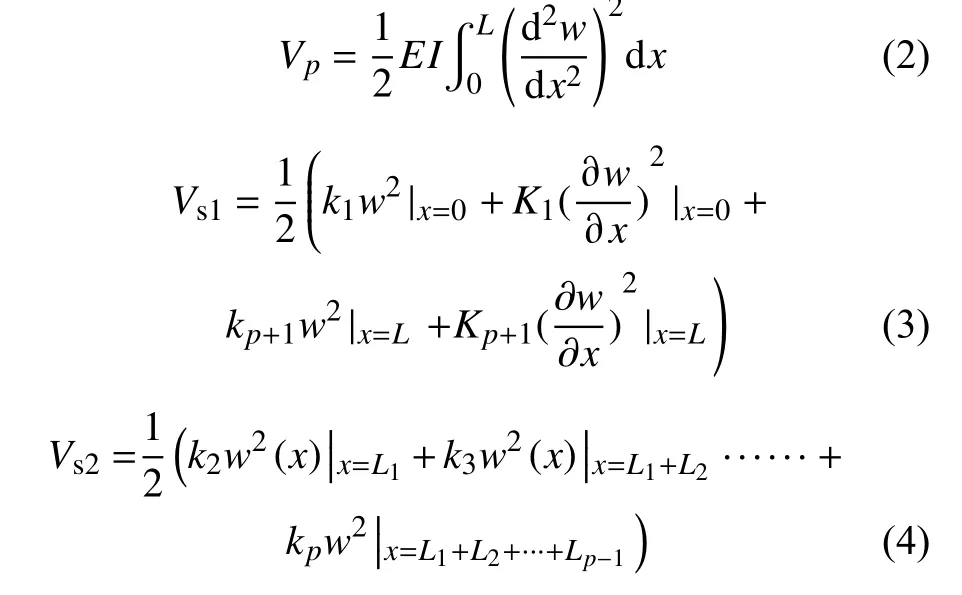
式中：Vp为多跨梁结构的应变能；Vs1为多跨梁结构边界处模拟弹簧的弹性势能；Vs2为多跨梁结构中间弹性支撑处支撑弹簧的弹性势能；E为弹性模量；I为截面惯性矩。

不考虑约束弹簧的质量，含弹性支撑的多跨梁的动能最大值为

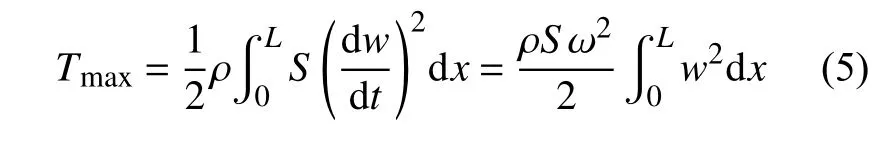
式中：S为梁的横截面面积；ρ为梁的质量密度；ω为圆频率。

多跨梁结构的拉格朗日函数[17]定义为

式中：Vmax为多跨梁结构的总势能最大值；Tmax为多跨梁结构的总动能最大值。

将式（1）～式（5）代入拉格朗日函数中，由瑞利—里兹法，拉格朗日函数应对式（1）中的各待定系数取极值，即

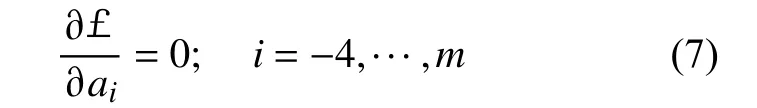
在实际计算中，式（1）中的位移级数不可能取无穷大，现将式（1）中n的最大值取为m。由式（7）可得到m+5 个线性方程组，矩阵化得

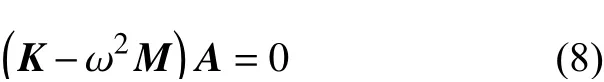
式中：K为刚度矩阵；M为质量阵；A为式（1）所示新型改进傅里叶级数中由未知系数组成的列向量，即

式（8）非零解的条件为

求解该矩阵特征值问题，即可得到任意边界约束条件下带有弹簧支撑的多跨梁结构的固有频率。将每个固有频率所对应的特征向量代入式（1），即可得多跨梁的模态。

2 数值计算与分析

采用Mathematica 软件进行编程求解。在以下叙述中，将简支边界记为S，自由边界记为F，固支边界记为C。

2.1 新型改进傅里叶级数下单跨梁收敛性

算例1。由于在新型改进傅里叶级数中，位移级数在计算过程中不可能取无穷大，因此截断数m的取值大小关系到本文结果的收敛性。为保证收敛性，选取S-S 边界下单跨梁结构进行收敛性分析。其中，无量纲固有频率定义如下：

表1 给出了单跨梁随截断数m变化时的前6 阶无量纲频率。根据表1，图2 示出了截断数与频率之间的折线图。

由图2 可知，为保证本文方法的收敛性，单跨梁的截断数一般取m=8 即可。由下文的算例可知，截断数的合理值与跨数p和频率阶数有关，其取值随跨数和阶数频率的增加而增大。在下文的算例中，3 跨梁时取m=10，5 跨梁时取m=12，8 跨梁时取m=18，10 跨梁时取m=22。

表 1 S-S 边界不同截断数时的前6 阶频率Table 1 The first six frequencies for different truncation numbers under the S-S boundary

图 2 截断数与频率之间的折线图Fig. 2 Line chart between truncation numbers and frequencies

2.2 不同截面下双跨梁的振动特性分析

算例2。考虑在中点处设置支撑的双跨悬臂梁，此时p=2，模型图如图3 所示。梁的长度为1 m，梁的截面为实心矩形截面，截面的宽和高为b×h=0.1 m×0.1 m，材料密度为7 850 kg /m3，弹性模量E=2.06 ×1011Pa。为模拟链杆，式（4）中，支撑横向弹簧的刚度值取为1014。计算得到含中间链杆支撑的前9 阶固有频率如表2 所示，并与文献[7]中的数值解进行了比较。结果显示，误差在1.5%之内，验证了本文方法的正确性。图4所示为中点链杆支撑的双跨悬臂梁的前2 阶模态图。

另外，为考察其他形状截面梁的振动特性，选取了工字形和T 形2 种截面，分别如图5 和图6所示。当工字形截面的B×H=0.05 m×0.12 m，b×h=0.04 m×0.08 m，T 形截面的B=0.05 m，H=0.12 m，b/2=0.02 m，h=0.02 m 时，其前9 阶频率也列于表2 中。由式（10）可知，对同种材料组成的多跨梁结构，如果改变截面形状，则其振动的固有频率与成正比。

图 3 矩形截面双跨梁模型Fig. 3 Double-span beam model of rectangular section

表 2 C-F 边界梁含中间链杆支撑前9 阶固有频率Table 2 The first nine natural frequencies of C-F boundary beam with intermediate chain support

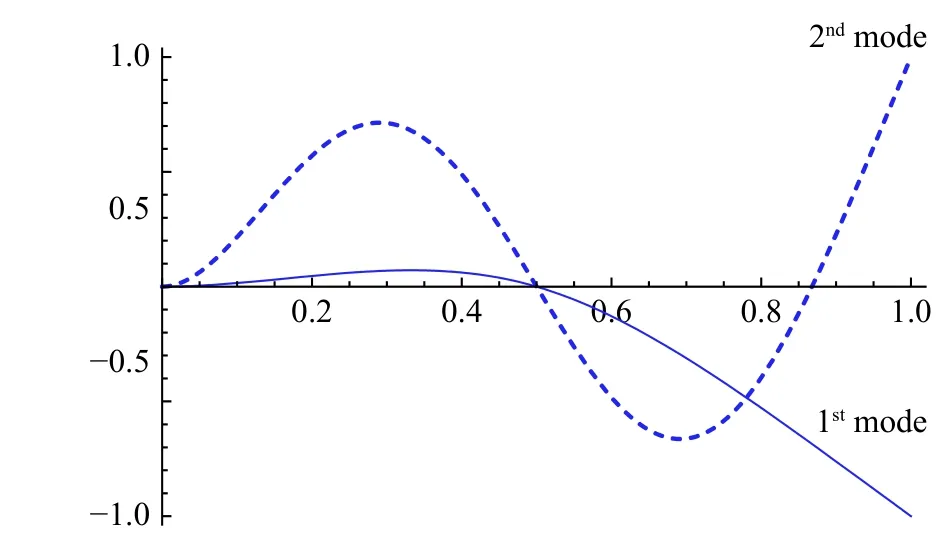
图 4 双跨悬臂梁模态Fig. 4 The modal of double-span cantilever beam

图 5 工字形截面Fig. 5 I-shaped sectionn

图 6 T 形截面Fig. 6 T-shaped section

当双跨悬臂梁的中间链杆支撑从最左端移动到最右端，即链杆支撑离最左端边界的距离a从0 m 变化到1 m 时，其前2 阶固有频率的变化情况如表3 所示，并与已有结果（根据文献[7]提供的解析频率方程计算）进行了比较，误差在允许范围内。由表3 可以看出：随着a的不断增大，悬臂梁的第1 阶固有频率不断增大，当a增大至接近右端边界时，固有频率开始逐渐减小；第2 阶固有频率在到达中间位置前不断增大，过了中间位置以后，开始逐渐减小。

表4 给出了两端简支和两端固支边界条件下，含中间链杆的支撑梁随链杆位置a变化时其前2 阶固有频率变化情况。图7 所示为以上2 种边界双跨梁自由振动的前2 阶固有频率随链的支撑位置变化的折线。

从图7 可以看出：对于两端简支和两端固支的梁，同悬臂梁类似，其第1 阶固有频率也是随着a的增加而不断增大，但当a＞0.5 m 时，随着a的增加，第1 阶固有频率逐渐减小；而第2 阶固有频率在链杆位于左半侧时，是随着a的增加先增大后减小，当链杆位于梁的右半侧时则是随着a的增加呈现先增大后减小的趋势。

表 3 C-F 边界双跨梁的前2 阶固有频率随链杆位置的变化Table 3 Variation of the first two natural frequencies of C-F boundary double-span beam with the location of chain bar

表 4 S-S 和C-C 边界双跨梁前2 阶固有频率随链杆位置的变化Table 4 Variation of the first two natural frequencies of S-S and C-C boundaries double-span beam with location of chain bar

图 7 双跨梁前2 阶固有频率随支撑位置变化图Fig. 7 Variation of the first two natural frequencies of double-span beam with location of chain support

2.3 不同截面下多跨梁的振动特性分析

算例3。研究含中间弹性支撑多跨梁的固有频率。选取边界条件为简支边界，梁的总长度L=1 m，等截面直径d=0.01 m，质量密度ρ=0.5 kg/m3，弹性模量E=2.02×1011Pa；弹性支撑弹簧分别取2，4，7，9 个，并恰好把梁分为若干相等段。图8 所示为10 跨梁示意图。表5 给出S-S 边界梁的若干固有频率，其中弹性支撑的横向弹簧刚度值均取107。同时，表5 还给出了当p=3 或5 时其前6 阶固有频率，以及当p=8 或10 时其前10 阶固有频率。经对比，可知表5 所示结果与文献[18]中的频率结果一致。工字形和T 形截面选取算例2 的截面尺寸。图9 和图10 分别为3 跨与5 跨圆形截面前2 阶模态示意图。

图 8 圆形截面10 跨梁模型图Fig. 8 The model of a ten-span beam with circular section

表 5 S-S 边界多跨梁的前10 阶固有频率Table 5 The first ten natural frequencies of S-S boundary multi-span beam

图 9 3 跨梁模态图Fig. 9 The modal of a three-span beam

采用算例3 中梁的数据。在C-C 边界多跨梁下，p=3，5，8，10 时其前2 阶频率随弹性支撑刚度值变化的固有频率如表6 所示。由表6 可知，任意p跨梁的前2 阶频率都是随着中间弹性支撑刚度值的增大而不断增加的，当增大达到一定限值（即链杆支撑）后，频率基本保持不变；随着跨数p的增加，弹性支撑梁的前2 阶固有频率逐渐减小。

图 10 5 跨梁模态Fig. 10 The modal of a five-span beam

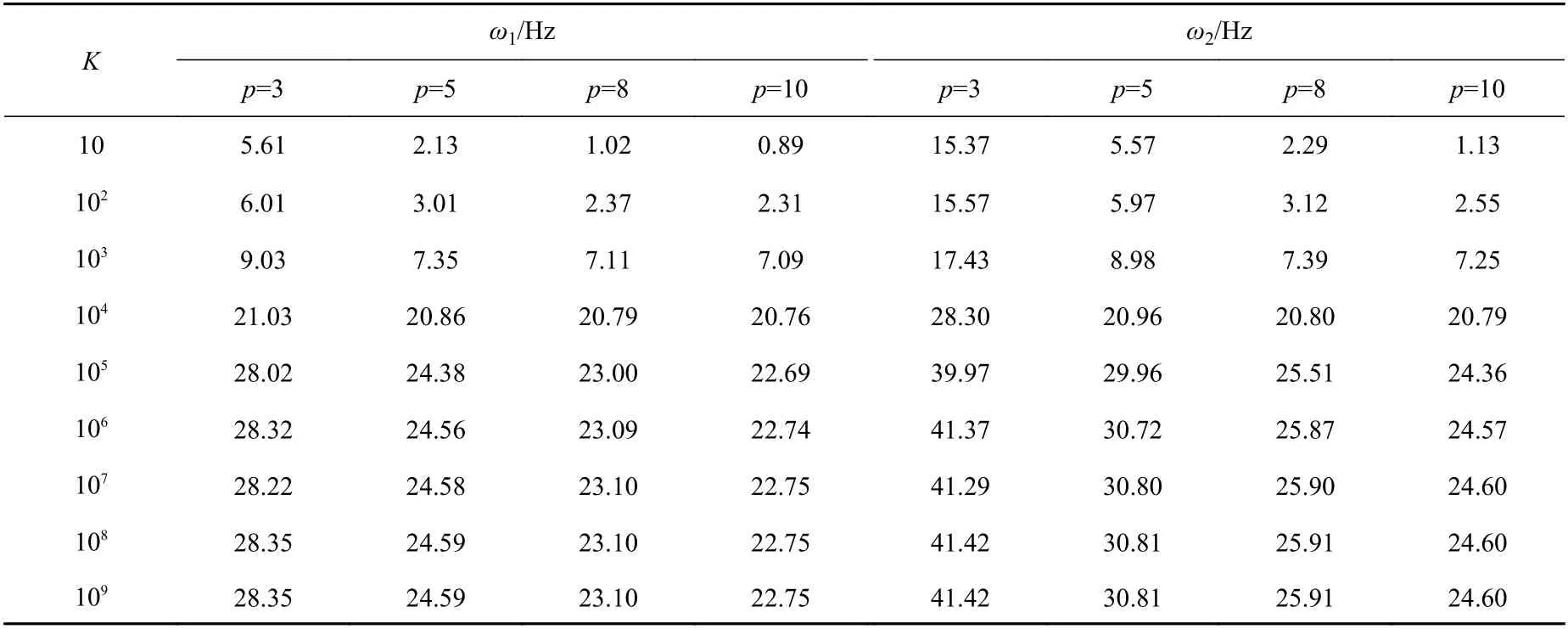
表 6 不同弹性支撑刚度值时C-C 边界多跨梁的前2 阶固有频率Table 6 The first two natural frequencies of C-C boundary multi-span beam with different elastic support stiffness values