碟旋体高速小角度入水稳定性仿真分析

张晓乐，彭松江，潘菲菲，杨兴林

1 郑州机电工程研究所，河南 郑州 450015

2 河南省水下智能装备重点实验室，河南 郑州 450015

3 江苏科技大学 能源与动力学院，江苏 镇江 212003

0 引 言

高速航行体以一定速度从空气介质中冲击入水水面，首先是其头部与水接触，此时流体质点随即向周边排开，并与高速航行体产生分离，随着入水深度的增加，在其运动轨迹上形成一个由空气和空化水蒸气构成的环体空泡，最后运动体完全进入水面以下形成完整的入水过程。该过程具有强瞬时、非定常及高载荷等特性。该过程的研究对于鱼雷、深水炸弹、反潜导弹投放，超空泡射弹打击水下目标和宇宙飞船的回收[1]等工程开发具有重要意义。

早期针对入水弹道的研究始于不自旋的鱼雷。国外学者，Waugh[2]和May[3]对弹体入水特点和试验结果进行了总结；矶部孝[4]研究了常规兵器水下弹道的运动规律，做了大量的试验，深入分析了弹丸入水的跳弹现象，并简要探讨了弹丸的稳定机理。在上述学者的研究基础上，国内也展开了试验研究。顾建农等[5]研究了球形与普通两种手枪弹丸倾斜入水的轨迹，发现高速旋转的普通制式弹丸的入水弹道存在不稳定的现象，且容易发生失稳翻转。张伟等[6]通过试验发现截卵形弹体由于受力不均衡，一般会在入水后发生偏转，而卵形弹体则在入水前期即发生了偏转。王云等[7]对4 种头型的非自旋的弹体在以60～140 m/s速度斜切入水时的弹道进行了研究，发现椭圆斜截头弹体容易产生偏向水面的弯曲弹道，入水角对弹道影响较为显著。从大量试验研究可以发现，高速航行体入水问题非常复杂，除了会在水面出现跳弹外，入水结构的水弹道也容易发散或失稳。

随着研究的深入，数值分析方法也广泛应用于高速航行体入水的研究领域。马庆鹏等[8]针对小型锥头圆柱体高速自由垂直入水问题，基于有限体积法（FVM）和流体体积（VOF）法开展数值模拟，得到了入水空泡演化过程和深闭合过程中的空泡流场流动特性及压力分布特性。方城林等[9]利用动网格技术，对5 种不同头型的轴对称高速射弹垂直入水过程进行了数值模拟，得到了射弹头部线型与入水速度衰减及入水阻力系数峰值变化的关系。张岳青等[10]以楔形和弧形体为研究对象，使用自行设计的装置进行了入水冲击试验，采用ALE 方法对不同入水工况下的加速度和压力相应进行了仿真分析。

以上研究多是基于圆柱体改进结构或宽面密闭腔体结构的入水特性，很少有碟形结构入水的研究。为解决较大尺度结构入水稳定性问题，设计了一种新型碟形体弹丸，并开展该结构小角度入水的稳定性仿真研究。本文将采用刚体拉格朗日结构网格和欧拉流场网格（L/E）耦合的数值仿真方法，首先，与典型圆柱体入水试验进行校对，校验仿真计算方法的准确性；然后，建立碟旋体和常见制式的尖头回转体仿真模型，模拟二者在以7°斜角入水时的初始弹道轨迹并对比计算结果；最后，模拟不同入水角度的碟旋体入水时的初始弹道，研究入水角度对碟旋体入水弹道稳定性的影响。

1 控制方程及计算方法

1.1 控制方程

采用Euler 方法模拟流体运动，建立流体域，并采用如下质量、动量和能量守恒控制方程。

质量守恒方程：

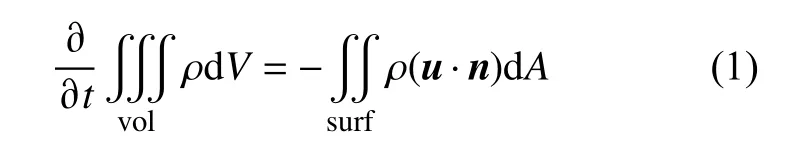
动量守恒方程：

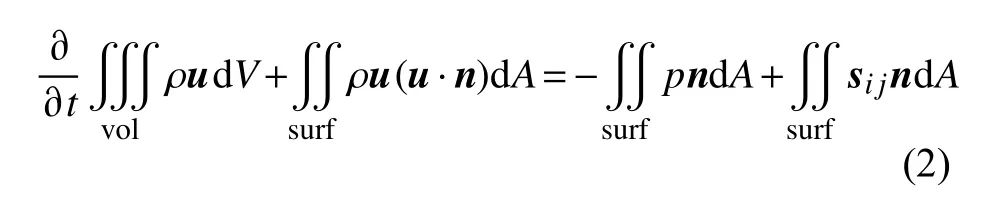
能量守恒方程：

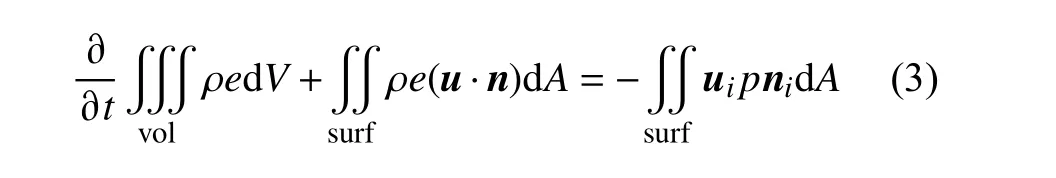
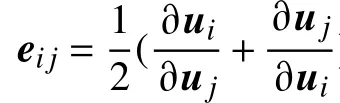
1.2 状态方程

状态方程定义了海水各种不同状态下的压力和密度以及比内能之间的函数关系，采用多项式方程的形式。

压缩状态（ µ＞0）：

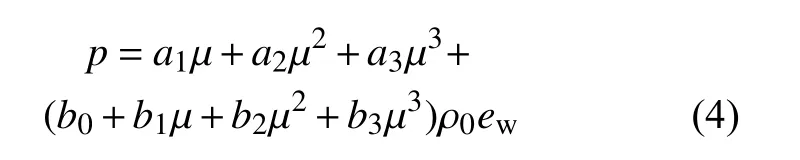
拉伸状态（ µ＜0）：

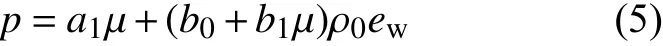
计算域中的空气，采用Gamma 状态方程：

式中：eg为 空气比内能； ρg为空气密度；γ为比热比，γ=1.4。

1.3 耦合算法

本文计算模型包括固体域和流体域。其中，固体域主要模拟碟旋体，采用Lagrange 方法设置为刚体网格来模拟；流体域包括海水和空气所填充的Euler 网格区域，采用Euler 方法模拟。两个计算域相互重叠。Lagrange 网格结构外部定义了一个封闭耦合面，用于传递两种计算域间的作用力。对于结构冲击动力分析，在每个时间步都对结构与流体间的接触状态进行判断，在接触冲击力的作用下，接触面的边界会发生变化。在航行体整个入水过程中，包含了材料非线性和接触非线性等一系列强非线性迭代计算。

2 计算模型

2.1 碟旋体模型

图1 所示为本文建立的碟旋体模型，从侧面看为圆盘状，从正面看为橄榄状。碟旋体轴线位于x-z平面内几何中心，其直径为0.4 m，轴向最大厚度为0.14 m。在建立碟旋体全三维模型时，采用了Lagrange 网格离散，并设置为刚体。为描述碟旋体三维弹道，其六个自由度不固定。相对于坐标系，碟旋体入水速度在x，z方向分别为−402 和−49.3 m/s，可实现7°角入水。碟旋体入水的初始水速度为405 m/s，入水前先以6 000 r/min转速绕回转轴线自旋。

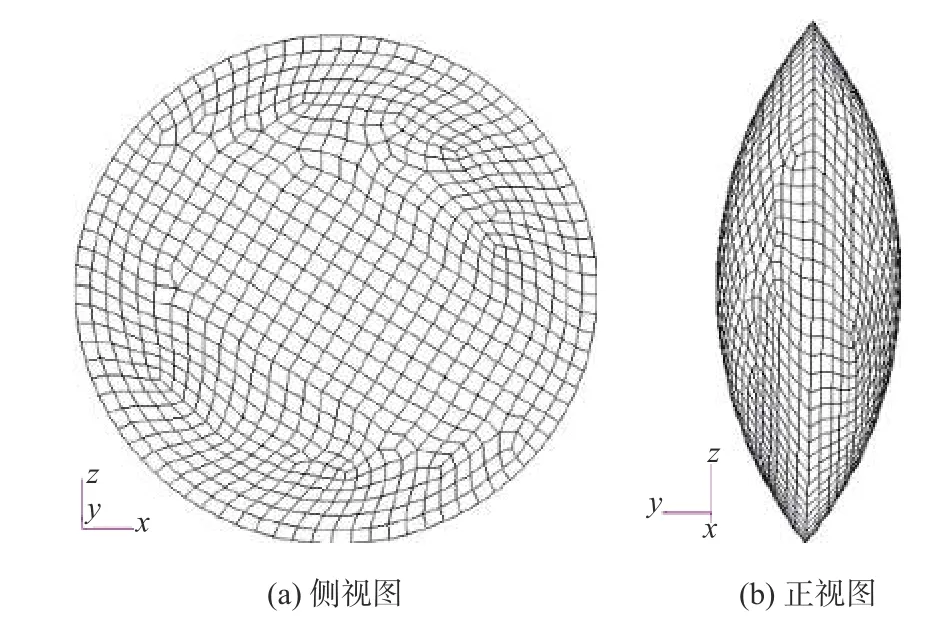
图 1 碟旋体模型Fig. 1 Model of the disc-spinning body

2.2 尖头回转体模型

图2 所示为建立的尖头回转体全三维模型，其轴线位于x-z平面内几何中心，直径为0.15 m，长为0.78 m。模型采用Lagrange 网格离散，并设置为刚体。为描述尖头回转体三维弹道，其6 个自由度不固定。尖头回转体轴线相对于水面呈7°角。尖头回转体初始速度在x，z方向分别为−402 和−49.3 m/s，入水初始速度为405 m/s，入水前回转体以6 000 r/min 转速绕轴线自旋。

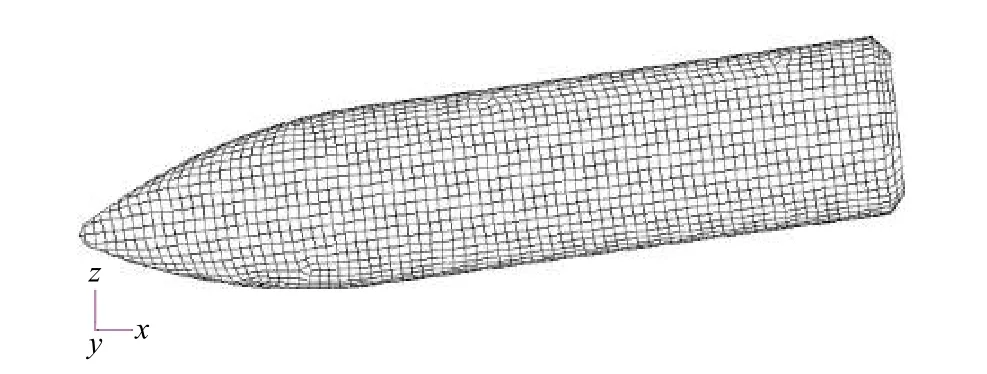
图 2 尖头回转体模型Fig. 2 Model of the cusp revolution body

2.3 流场模型

图3 所示流场计算域为一个长20 m、宽1.6 m、高3.2 m 的区域。其中，上部（0.3 m 高）为1 个大气压的空气介质区域，下部（2.9 m 深）为水介质区域。流场计算域边界均为压力边界，水介质压力边界随水深进行赋值。碟旋体初始位置在空气中，底部接近于水面。为保证计算精度，在碟旋体运行轨迹区域进行了网格加密。

图 3 流场计算域及边界条件Fig. 3 The fluid computational domain and boundary conditions

3 计算方法验证

将本文所用算法的计算结果与文献[12]柱形结构高速入水试验结果进行了对比，以校核算法的准确性。试验选用的平头圆柱体弹丸直径6 mm、长24 mm，通过高速垂直入水试验，测得的入水初始速度为141 m/s。本文根据此试验参数建立了如图4 所示仿真模型。仿真模型考虑了入水时的气—液界面上的惯性力、重力、流体阻力及空化效应等影响入水过程的各项因素。图5 所示为仿真计算获得的位移与试验结果对比。由图可见，在入水时刻t=2.4 ms 时，仿真结果相对于试验入水结果（深度）相差约10.1%，这说明仿真与试验入水结果值吻合较好，所用算法合理可信。

图 4 平头圆柱体90° 角垂直入水仿真(t = 2.4 ms)Fig. 4 The simulation of a flat-head cylinder at 90° angle of water entry (t = 2.4 ms)

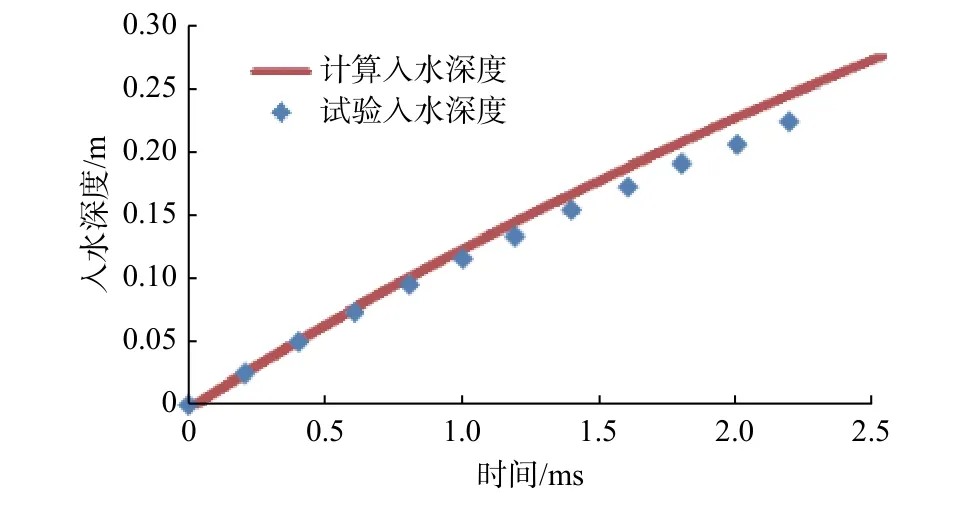
图 5 仿真计算得到的位移结果与试验入水结果对比Fig. 5 Comparison between simulation and displacement obtained by water entry experiment

4 入水仿真计算结果对比

4.1 尖头回转体7°角入水过程仿真结果

图6 和图7 分别给出了高速自旋尖头回转体以7°角高速斜切入水过程的仿真结果。从计算结果可以看出，尖头回转体入水过程中头部姿态先上扬至水平，随后逐渐上翘且弹体在水面弹起，进而在空中翻转，姿态失稳严重，这说明了采取小角度入水时的稳定性差。

图8 所示为尖头回转体以7°角高速斜切入水仿真过程质心运动轨迹，可见尖头回转体触水后很快出现明显的弹起现象，导致其无法稳定入水。

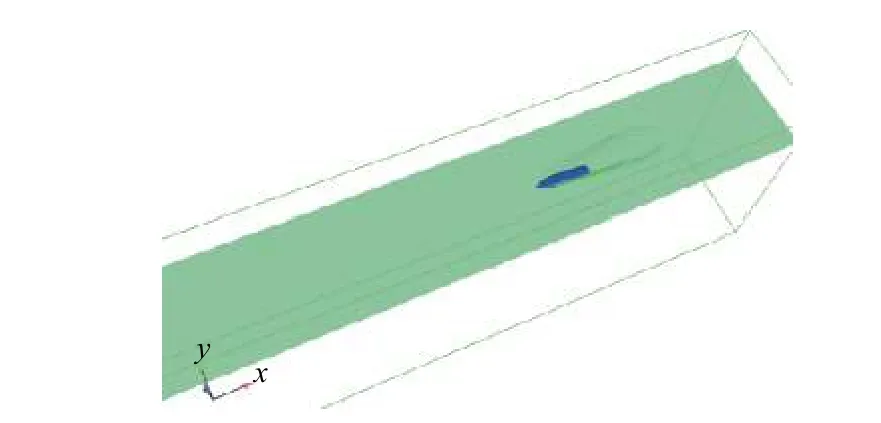
图 6 t = 8 ms 时尖头回转体的入水斜视图Fig. 6 Oblique view of cusp revolution body as entering water at t = 8 ms

图 7 t = 19.5 ms 尖头回转体姿态斜视图Fig. 7 Oblique view of attitude of cusp revolution body as entering water at t = 19.5 ms

图 8 尖头回转体以7°角入水时的初始弹道轨迹Fig. 8 Initial trajectory of cusp revolution body at 7° angle of water entry

4.2 碟旋体7°入水过程仿真结果

图9～图10 给出了碟旋体以7°角高速斜切入水过程的仿真结果。当碟旋体沿水平x方向运动20 m、入水深度1.63 m 时，发现速度方向的碟旋体后半部发生局部空化，但在整个入水过程中姿态未发生失稳，在水中后仍沿直线弹道前进，未发生跳弹、翻转和偏转等现象。图11 给出了碟旋体以7°角高速斜切入水过程中的质心运动轨迹。从图中可以看出，碟旋体入水后直到出计算域（长达20 m）的这段距离内，其在x-z平面内水中的弹道没有弯曲。弹道计算入水深1.63 m时，侧向偏斜不到0.03 m，弹道稳定性好。对照本文4.1 节的计算结果可见，相比于常见的制式尖头回转体，碟旋体的入水稳定性较好。根据文献[4]的研究，尖头弹体入水时，因冲击而产生升力作用，使得沿弹轴线运动的弹道不稳定。本文所设计的碟旋体头部入水冲击面积小，入水冲击产生的升力也较小；另一方面在入水过程中，碟旋体绕轴线高速自旋，根据陀螺稳定原理，此时具有较好的姿态稳定性。

图 9 碟旋体以7°角入水时的侧视图(t = 40 ms)Fig. 9 Side view of disc-spinning body at 7° angle of water entry(t = 40 ms)

图 10 碟旋体以7°角入水弹道末时刻侧视图（t = 100 ms）Fig. 10 Side view of 7° angle water entry of disc-spinning body at the end of the trajectory（t = 100 ms）

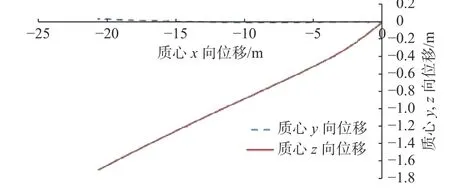
图 11 碟旋体以7°角入水的初始弹道轨迹Fig. 11 Initial trajectory of disc-spinning body at 7° angle of water entry

5 入水角度对入水稳定性的影响

为验证碟旋体多种角度入水的稳定性，本文开展了碟旋体以多个角度（16°，26°，36°和45°）入水初始弹道的仿真。图12 给出了碟旋体以45°角高速斜切入水过程的仿真结果。当碟旋体沿水平x方向运动14 m、入水深度13.95 m 时，发现整个入水过程中碟旋体未发生失稳，在水中仍沿直线弹道前进，未发生跳弹、翻转和偏转等现象。

图13 给出了碟旋体以45°角高速斜切入水过程中的质心运动轨迹。从图可以看出，在碟旋体入水后直到出计算域（长达20 m）的这段距离内，碟旋体在x-z平面内水中的弹道没有弯曲。这说明碟旋体以45°这种较大角度入水时仍具有很好的弹道稳定性。

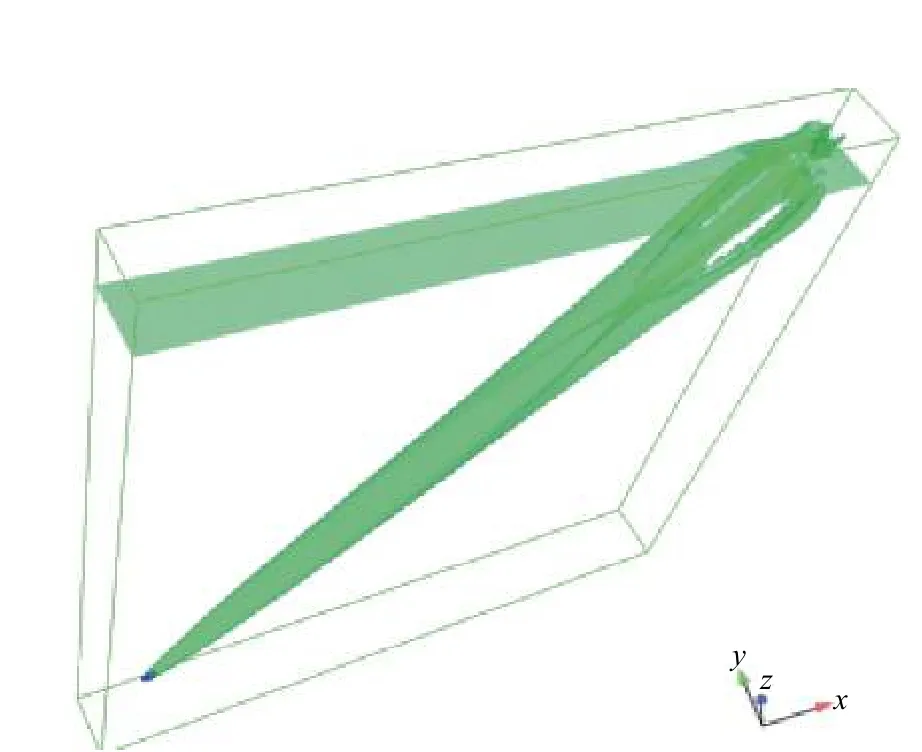
图 12 碟旋体以45°角入水弹道末时刻斜视图（t = 101 ms）Fig. 12 Side view of disc-spinning body 45°water entry at the end of the trajectory（t = 101 ms）

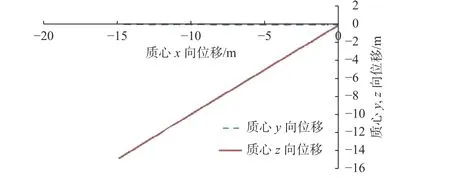
图 13 碟旋体以45°角入水的初始弹道轨迹Fig. 13 Initial trajectory of disc-spinning body at 45°of water entry

基于上文对7°和45°入水计算，图14 给出了碟旋体以16°，26°和36°角高速斜切入水过程质心运动轨迹。从图可以看出，碟旋体入水后在x-z平面内水中的弹道仍呈直线，没有弯曲。在入水轨迹长达15 m 时，碟旋体侧向偏斜均小于0.12 m，弹道偏斜也较小，这说明碟旋体以多个角度斜切入水时弹道稳定性均较好。

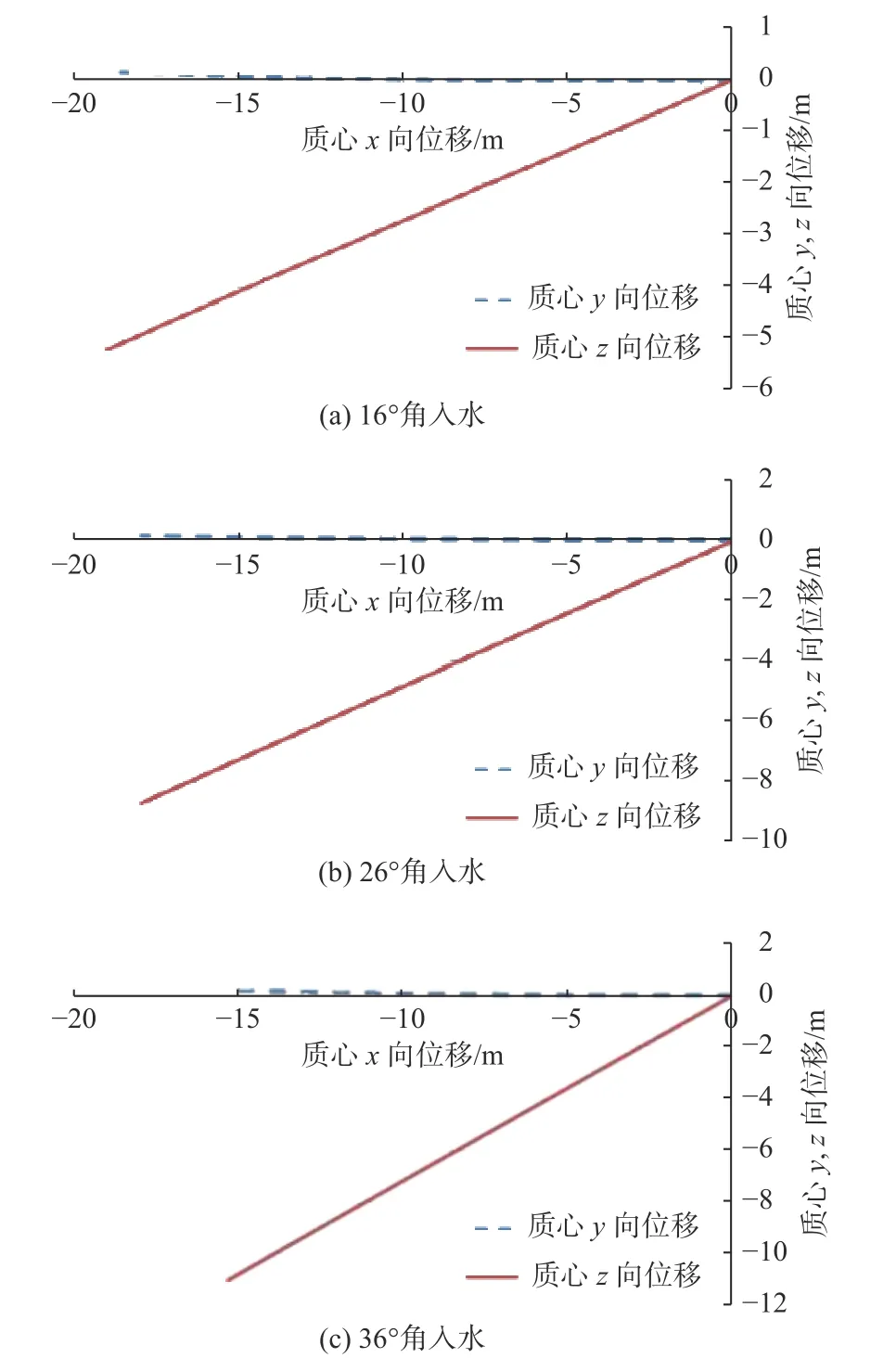
图 14 碟旋体以不同角度入水时的初始弹道轨迹Fig. 14 Initial trajectories of disc-spinning body at different angles of water entry

6 结 语

本文采用Lagrange 结构网格和Euler 流场网格耦合的方法，开展了碟旋体和尖头回转体弹丸以7°小角度入水时的弹道稳定性对比分析，结果表明，尖头回转体弹丸入水时发生了跳弹现象，碟旋体弹丸在此小角度下不但能够入水，而且弹道稳定。通过对碟旋体以不同角度（16°，26°，36°和45°）入水时的初始弹道仿真，发现了上述角度下入水的弹道侧向偏斜较小且稳定。本文研究结果可以为水面平台向水下靶标精确、稳定和高速投放有效载荷提供新的方法和思路。