多液舱晃荡与养殖工船时域耦合运动的数值模拟
2020-06-03肖凯隆陈作钢
肖凯隆,陈作钢
1 上海交通大学 海洋工程国家重点实验室,上海 200240
2 高新船舶与深海开发装备协同创新中心,上海 200240
3 上海交通大学 船舶海洋与建筑工程学院,上海 200240
0 引 言
我国是海水养殖发达国家之一,养殖面积和产量均居世界首位[1]。现阶段,我国海水养殖方式还比较粗放,且内陆和沿海的养殖空间受到挤压,导致养殖密度过大、病害频发、水产品品质下降和环境恶化等问题日益突出[2]。因此,走向深远海、发展绿色养殖生产新方式已成必然趋势。
深远海养殖工船作为深远海养殖的一个发展方向,集成了繁育、养殖、加工、冷冻冷藏等鱼货物供给的一条龙功能,可为阶段性的分舱养殖、自动化投喂、自动排污、机械化起捕等提供先进的养殖和生产手段。依托养殖工船进行深远海养殖,可以实现高度集约化、生态化、规模化的健康养殖,同时将鱼类养殖区域推向深远海,能拓展养殖空间,有效地推进海洋渔业的转型发展[3]。养殖工船通常系泊工作于水质和风浪条件合适的深远海海域,并汲取海水至养殖液舱。但液舱晃荡产生的晃荡力作用于船体,可能会加剧船体运动,使船舶安全性面临更大的挑战。因此,在设计阶段对液舱晃荡与船体运动的耦合作用进行充分论证,是确保养殖工船安全性的关键。
目前,国内外许多学者针对液舱晃荡与船体时域耦合运动展开了研究。其中,液舱晃荡的模拟方法主要有2 类:非线性势流方法[4]和黏流方法[5]。船体运动预报主要基于势流理论,采用脉冲响应函数(IRF)法。船体运动预报和液舱晃荡模拟分别采用势流和黏流的方法,简称为势流—黏流耦合法;如果都采用势流方法,则简称为全势流法。全势流法假设舱内液体无黏无旋,但当晃荡剧烈时,该假设就会出现局限性。势流—黏流耦合法是基于CFD 理论模拟液舱晃荡,以牺牲计算效率为代价来提高计算精度。势流—黏流耦合法兼顾了势流方法计算速度快以及CFD 方法相对准确的优点,基于此,李裕龙等[6]和操戈等[7]将计算结果与试验结果进行对比,验证了该方法的可靠性。
本文将采用势流—黏流耦合法计算液舱晃荡与船体运动耦合的问题。首先,通过SESAM 软件计算船体水动力系数及波浪力,基于IRF 法计算时延函数,建立船体运动预报方程。接着,通过FLUENT 软件数值模拟液舱晃荡,采用流体体积(VOF)法捕捉自由面,并将液舱晃荡力实时添加至船体运动方程,让船体运动方程求解与液舱晃荡模拟交替进行,以随着时间的步进,重复解耦工作,然后在自由横摇衰减试验的基础上验证该方法的有效性。最后,计算得到船体运动幅值响应算子(RAO),对比分析考虑液舱晃荡力与不考虑液舱晃荡力下的计算结果,探究液舱晃荡力对船体运动的影响。同时,还将研究壁面剪切力对数值模拟液舱晃荡准确度的影响,并针对多液舱模型,探索一种二维计算方法,以极大地减小计算规模。
1 载液船舶在波浪上的运动预报理论
1.1 速度势叠加理论
势流理论假设流体无黏无旋,并引入速度势φ描述流场。φ满足

式中, ∇为拉普拉斯算子。
根据叠加原理,可以把速度势分解为入射势φI、绕射势φD、辐射势φR,如果只保留一阶项,则得到

各项速度势沿船体表面积分可得到流体对船体的各项作用力。其中,入射力FI是假设船体不存在时入射波在船体本该存在的位置产生的力;绕射力FD是假设船体固定时入射波绕射过船体所产生的力;辐射力FR是假设水面静止时船体运动所产生的力。因此,一阶波浪力为
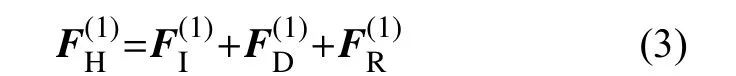
1.2 船舶频域运动方程
根据牛顿第二定理,刚性船体的运动方程为

式中:M为船体质量矩阵; ξ¨为船体加速度;FS=−Kξ ,为船体回复力,其中K为回复系数矩阵, ξ为船体位移;FL为船体受到的其他外力,如液舱晃荡力。
根据辐射力的相关理论,FR为

将式(3)和式(5)代入式(4),得到船体频域运动响应方程
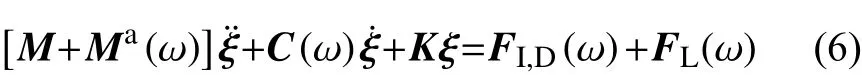
式中: ω为波浪频率;FI,D为Froude-Kriloff 力,为入射力与绕射力之和,表示船体在规则波中受到的波浪激励力[8]。
流体黏性对船体运动,特别是横摇运动影响很大,通常是对横摇阻尼添加线性项来弥补势流理论中黏性的缺失。

式中, γ为临界阻尼系数,其取值与船型有关,无舭龙骨时,其取值范围为2%~4%[9]。
1.3 基于脉冲响应函数法的载液船舶时域运动方程
将船体在波浪中的响应看作线性系统,通过IRF 法可以将一阶波浪辐射力表示成时延函数R(t)与速度时历 ξ˙(t)的卷积形式[10]。

式中:R为时延函数;t为时间;τ为时间积分量;ij为矩阵角标。无穷大遭遇频率的附加质量和Rij(t)为

将式(6)中的波浪激励力FI,D和液舱晃荡力FL用时历的形式表示,同时将波浪辐射力用式(8)表示,得到液舱晃荡与船体运动时域耦合方程为
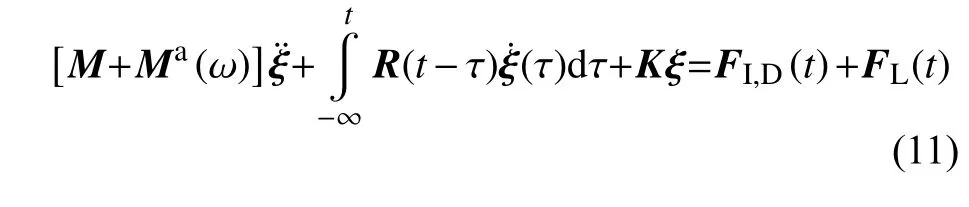
2 时域耦合方程的数值计算方法
本文将基于水动力学软件SESAM 计算船体质量、附加质量、阻尼系数和波浪载荷等水动力系数,基于CFD 软件FLUENT 数值模拟液舱晃荡,并在用户自定义函数(UDF)中实时将晃荡力添加至船体运动方程。具体运算步骤为:
1) 采用SESAM 软件计算船体水动力系数,直接输入或等待UDF 读取;
2) 给液舱设置微小的初始速度作为第1 个时间步的边界条件;
3) 采用软件FLUENT 计算当前时间步的液舱晃荡力,并添加至船体运动方程;
4) 求解船体运动方程,给出下一时间步的船体运动速度,并将其作为液舱新时间步下的运动边界条件;
5) 步骤3)和步骤4)交替进行,随着时间的步进,重复解耦工作,直至计算结束。
本次参观交流活动,为双方在战略层面上达成了共识,作为国内钟表行业唯一的研究所与目前国际上顶级的机心制造商来说,不断的加强交流与合作,不仅是达成双方共赢的商业目的,更多是企业发展理念的契合,乃至为钟表行业发展尽一份力量。
UDF 的编制及计算过程需考虑以下细节:
1) UDF 在软件FLUENT 中运行时,新时间步下自定义物理量会被重新定义,而求解船体运动方程需要参考历史物理量,因此要将有关物理量定义成静态变量,以避免在新时间步被清空。
2) 为避免每一时间步都要重新计算时延函数,可编写外部程序预先计算,并在UDF 运行的初始时刻读取。
3) 船体水动力是基于船体运动重心位置确定的,转换液舱晃荡力至船体运动方程或将船体运动响应转换至液舱晃荡边界条件时,需要根据实际情况确定。
3 不规则多液舱简谐晃荡的数值模拟
3.1 养殖工船物理模型
养殖工船垂线间长241 m、型宽48 m、型深18.5 m,经快速性多目标数值优化[11],得到型线图如图1 所示。在主甲板下设置了关于船舯对称的6 对养殖水舱,其中艏、艉2 对为不规则液舱,船舯4 对为尺寸一致的矩形规则液舱,各液舱高度均为16.1 m,载液率为75%。图2 所示为液舱简化俯视图,图中仅绘制了1 对规则液舱来代替4 对规则液舱。

图 1 养殖工船型线图Fig. 1 Lines plan of the aquaculture ship

图 2 液舱俯视图Fig. 2 Top view of the multi-tank
3.2 壁面剪切力对液舱晃荡数值模拟的影响
正确处理壁面黏性效应,是CFD 数值模拟的关键。壁面函数法是常用的壁面处理方法,其本质是在黏性子层及过渡层使用称为壁面函数的半经验公式计算壁面与充分发展湍流区域之间的黏性影响区域。壁面函数的使用依赖于壁单位(Wall unit)y+的正确选取,y+表示第一层网格与壁面间的无量纲距离,其计算公式可参考文献[13]。当壁面函数选取增强壁面处理(Enheanced wall treatment)时,要求y+保持在5 以下。
壁面函数法对y+的要求导致壁面附近的网格量剧增、计算时间变长。若壁面黏性效应对液舱晃荡影响极小,不妨将壁面设置为滑移壁面,此时壁面附近没有强剪切,离壁第1 层网格的高度也不再受壁面函数的约束。本文设置了3 组案例(Case1, Case2, Case3)来对比验证壁面剪切力对液舱晃荡数值模拟的影响。
3 组案例均采用30 m×16 m 的二维矩形液舱,载液率均为50%,液舱绕其中的点作频率为0.085cos0.6trad/s 的横摇运动。其壁面函数的选择与网格划分情况如表1 所示。

表 1 计算案例的网格及壁面处理模型Table 1 Mesh and wall treatment model for calculating cases
Case1 与Case2 均采用壁面加密结构网格,如图3 所示。要满足y+小于5,Case1 采用增强壁面处理的壁面函数法;Case2 选择滑移壁面作为边界条件,忽略壁面剪切力;Case3 采用均匀的结构网格,同样忽略壁面剪切力。

图 3 Case1,Case2 采用的精细化网格及其边界层Fig. 3 Refined mesh and boundary layer used in Case1 and Case2
图4 为3 组案例相对回转中心的晃荡力矩系数d的计算结果。由图可见,3 条曲线基本重合,但由于网格单元数减少了90%以上,导致Case3的计算时间减少了约80%。因此,可以认为壁面剪切力对液舱晃荡的数值模拟影响不大,可以选择滑移壁面作为壁面条件,同时采用均匀的结构网格,降低网格数量,提高计算效率。

图 4 相对回转中心的壁面力矩系数Fig. 4 Moment coefficients relative to the center of rotation
4 数值求解方法的有效性验证
为了验证本文数值方法的有效性,本节对养殖工船模型在载液率为62.5%时的静水横摇自由衰减试验进行了数值模拟。
4.1 横摇自由衰减运动的模型试验
试验在上海交通大学循环水槽中进行,该水槽试验段长8 m,宽3 m。根据水槽尺寸,试验模型缩尺比选为1∶100。试验开始前,利用惯量架测量船模转动惯量及重心位置。安装、调整压载铁,使吃水位于设计水线处,并记录压载铁的数量和位置。
试验时,人工施加恒力于一侧船舷,使船体产生稳定的初始横倾角,当船体内、外水静止后释放船体,船体开始做自由横摇衰减运动,同时用陀螺仪记录横摇角时历。图5 所示为载液及压载铁安装示意图。

图 5 载液及压载铁安装示意图Fig. 5 Water in tanks and ballast iron installation
4.2 数值模拟结果与试验结果对比
在已知船模、压载铁、液舱水体的重心位置和质量的情况下,根据初稳性理论可以求出横摇回复力系数K。假设船体绕着重心所在轴线做自由横摇,可以求出转动惯量。采用SESAM 软件计算横摇阻尼系数及附加转动惯量。
FLUENT 数值模拟液舱晃荡中,经网格无关性验证,设置液舱模型网格尺寸为6 mm,时间步长为0.005 s,迭代步数为60。
图6 所示为试验与数值模拟得到的横摇角时历对比图,图中同时还绘制了不考虑液舱晃荡的模拟结果。可以发现,考虑液舱晃荡的数值模拟结果与试验结果吻合良好,证明本文数值方法对液舱晃荡与船体运动耦合方程的求解有效。

图 6 试验与数值模拟的横摇角时历对比Fig. 6 Comparison of roll angle between test and numerical simulation
5 实船计算结果与分析
5.1 船体水动力系数、时延函数及CFD 参数设置
横摇临界阻尼系数λ取3%时,SESAM 软件计算得到的横摇阻尼系数C44如图7(a)所示;由式(10)计算出的时延函数R44如图7(b)所示;波高2 m时的一阶波浪横摇力矩F44如图7(c)所示。
液舱晃荡的数值模拟中,经网格无关性验证,网格模型尺寸取为0.6 m,时间步长为0.005 s,每一时间步的迭代步数为20。初始时刻液舱自由面示意图如图8 所示。
5.2 RAO 时域计算结果
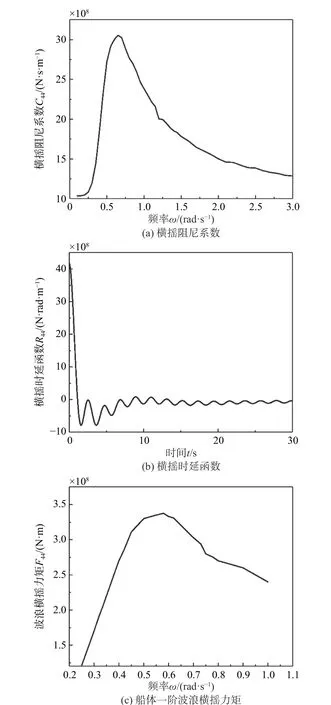
图 7 横摇阻尼系数、时延函数以及一阶波浪横摇力矩Fig. 7 Damping coefficient and retardation functions of rolling and First-order wave rolling moment

图 8 初始时刻液舱自由面示意图Fig. 8 The free surface of tanks in the initial moment
图9 所示为横向规则波激励下,考虑液舱晃荡力和不考虑液舱晃荡力情况下计算得到的横摇RAO4及升沉RAO3。如图9(a)所示,当波浪频率较低时,液舱晃荡力会加大船舶横摇运动幅值;而在波浪频率较高时,横摇幅值有所降低,液舱起到了减摇水舱的作用。同时,考虑液舱晃荡力时,RAO4的峰值较不考虑液舱晃荡力时的情况增大了43%,且峰值对应的波浪频率有所降低。如图9(b)所示,当波浪频率较低时,液舱晃荡力会加大船舶升沉运动幅值;而在波浪频率较高时,船舶运动幅值有所降低。考虑液舱晃荡力后,RAO3在频率更低的位置达到了峰值,且峰值略大于不考虑液舱晃荡力的情况。
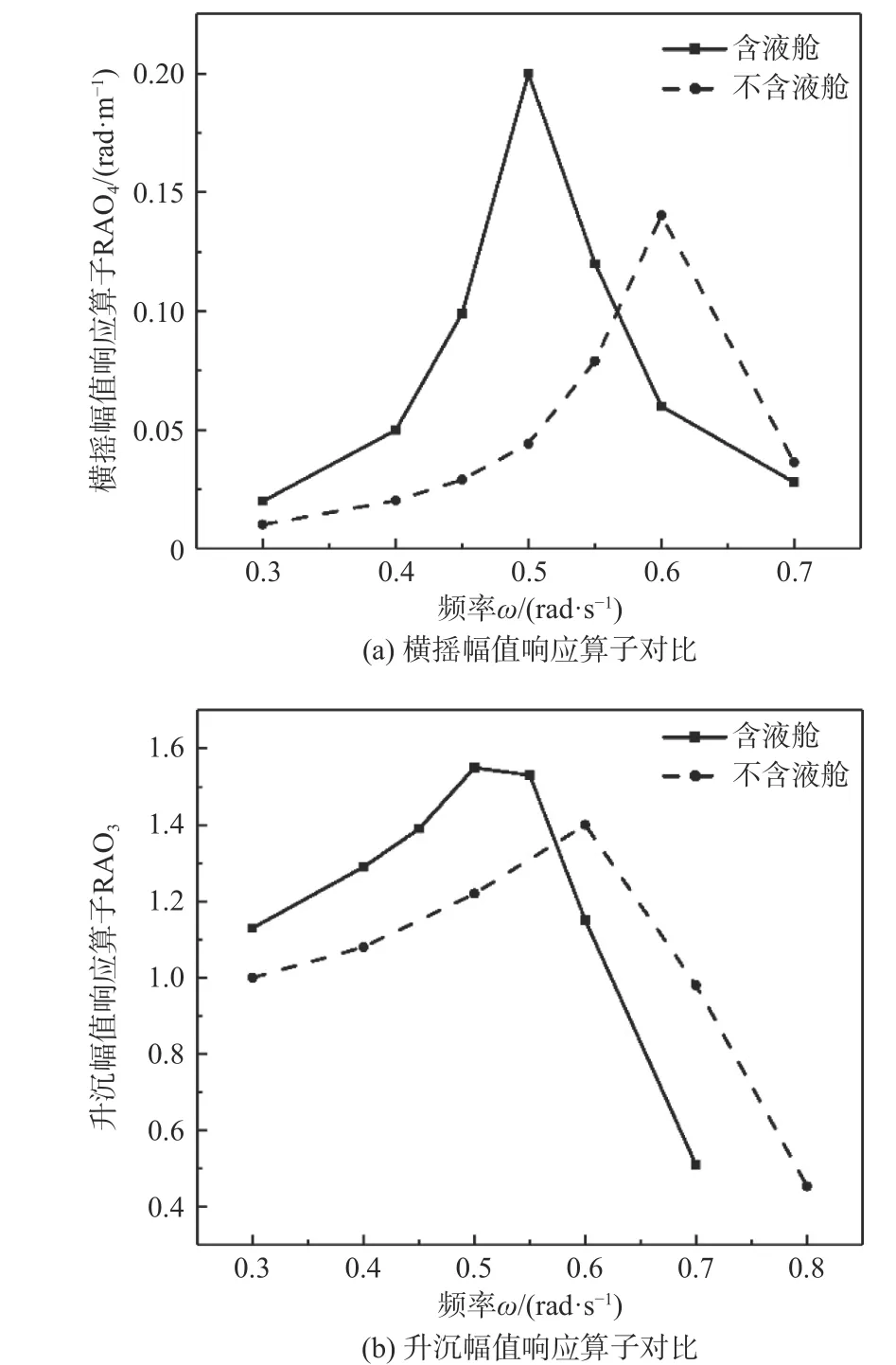
图 9 横摇、升沉幅值响应算子对比Fig. 9 Comparison of roll and heave response amplitude operator
5.3 液舱晃荡力对养殖工船运动的影响
如图9(a)所示,在波浪频率ω=0.4,0.6 rad/s的激励情况下,液舱晃荡力会分别增大、减小船体横摇运动幅度。本节将对比分析横摇运动时历及有关力矩,以说明液舱晃荡力对船体运动的影响机制。
图10(a)所示为在波浪频率ω=0.4 rad/s 的横向规则波激励下,考虑液舱晃荡力和不考虑液舱晃荡力的船体横摇运动时历ξ4(t)对比,图10(b)所示为晃荡横摇力矩与波浪横摇力矩时历F4(t)的对比。从中可以看出,运动稳定后,晃荡横摇力矩与波浪横摇力矩的相位十分接近,此时,液舱晃荡力将增大船体横摇运动幅度。
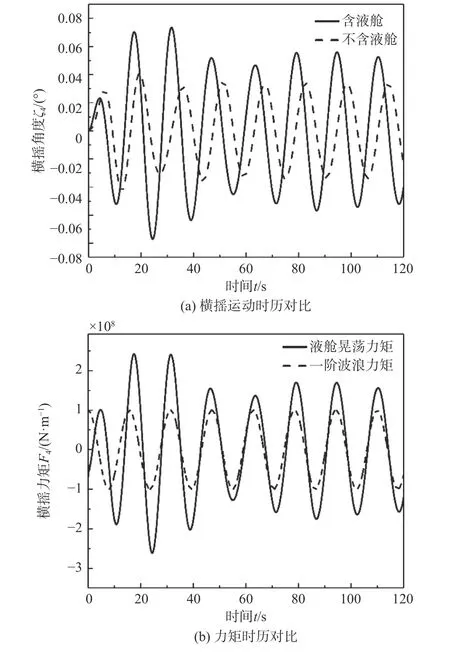
图 10 船体运动及相关力矩的对比(ω=0.4 rad/s)Fig. 10 Comparison of hull motion and moment(ω=0.4 rad/s)
图11(a)所示为在波浪频率ω=0.6 rad/s 的横向规则波激励下,考虑液舱晃荡力和不考虑液舱晃荡力的船体横摇运动时历对比,图11(b)所示为晃荡横摇力矩与波浪横摇力矩的时历对比。从中可以看出,运动稳定后,晃荡横摇力矩与波浪横摇力矩相位相差较大,此时,液舱晃荡力将降低船体横摇运动幅度。
6 多液舱晃荡的二维简化计算
本文虽然用1 对规则液舱代替了4 对规则液舱,但受限于计算规模,仍有必要进一步简化计算模型。图12 所示为波浪频率ω=0.5 rad/s 时,艏、艉液舱横摇力矩与4 对规则液舱横摇力矩的对比,从中可以看出,前者数值较小,因而对船体运动的影响有限。
图13 所示为液舱总横摇力矩与规则液舱横摇力矩的比值k随频率ω的变化示意图。如图所示,k的变化范围很小,可近似认为总力矩与规则液舱力矩间的比值恒定。因此,可选取某一波浪频率下的k作为所有频率下的定值,并将k倍的规则液舱力矩近似看作总力矩,以避免计算艏、艉不规则舱。波浪频率ω=0.5 rad/s 对应的k值为1.131,选其为本文定值k。

图 11 船体运动及相关力矩对比 (ω=0.6 rad/s)Fig. 11 Comparison of hull motion and moment (ω=0.6 rad/s)

图 12 规则舱与不规则舱横摇力矩对比(ω=0.5 rad/s)Fig. 12 Comparison of rolling moment between regular tank and irregular tank (ω=0.5 rad/s)
矩形液舱长、宽比大于1 时,三维液舱晃荡与二维液舱晃荡的数值模拟结果经过长度换算后吻合良好[14]。养殖工船规则液舱的长宽比约为1.6,可数值模拟其二维横截面液舱晃荡,并将晃荡力乘以液舱长度代替三维液舱的晃荡力,以进一步简化模型。
通过引入参数k替代艏、艉不规则舱的晃荡模拟以及采用二维模型代替三维液舱模型的策略,可将计算效率提升90%以上。

图 13 k 随频率ω 的变化Fig. 13 Variation of k with respect to frequency ω
图14 所示为在波浪频率ω=0.3,0.7 rad/s 的激励下,通过二维方法计算的与包含不规则液舱的三维方法计算得到的船体横摇运动时历对比。虽然k取波浪频率ω=0.5 rad/s 对应的值,但在波浪频率ω=0.3,0.7 rad/s 情况下的横摇运动模拟中,二维计算结果与三维计算结果吻合良好,表明用单一波浪频率下的k近似代替其他频率下的k是可行的。同时也表明,用二维液舱模型代替三维规则液舱模型来计算液舱晃荡是可行的。
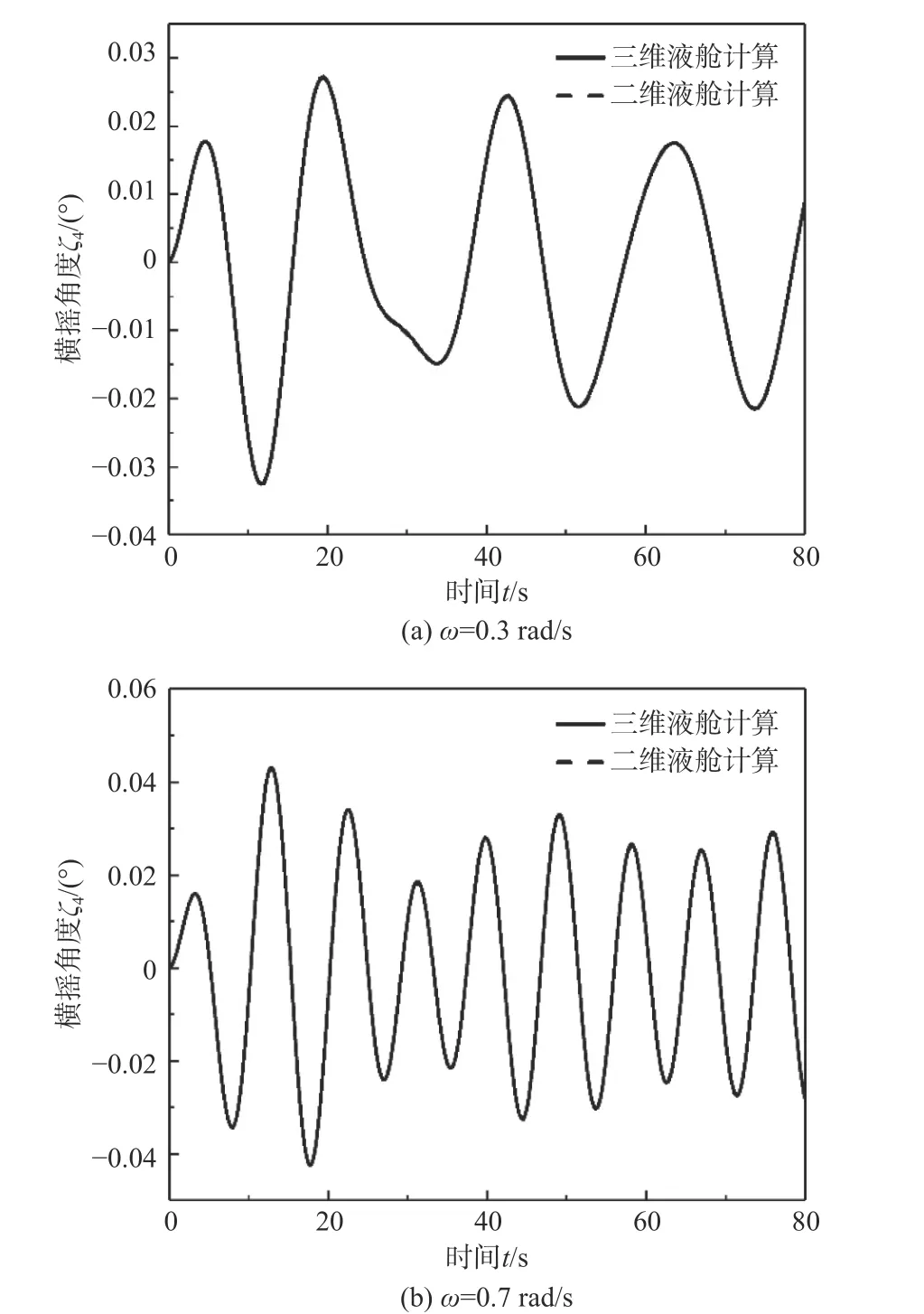
图 14 二维和三维液舱晃荡船体横摇运动时历对比Fig. 14 Comparison of ship rolling between 2D and 3D mutli-tank
如图9(a)所示,在波浪频率ω=0.5 rad/s 时RAO4达到峰值,该频率下,波幅为1 m 的横向波浪可使船体横倾角最大达到11.5°。图15 所示为在该波浪激励下,船体运动稳定后左倾、右倾达到最大位置以及在中间位置处(从左到右)的液舱晃荡云图。从中可以看出,由于周期较大,横摇角度较小,即使在RAO4峰值对应的波浪条件下,舱内水体的晃荡依然比较平稳,自由液面也未发生明显形变。

图 15 不同时刻的液舱晃荡云图(ω=0.5 rad/s)Fig. 15 The contours of tank sloshing at different times
7 结 论
本文求解了多液舱养殖工船在横向规则波激励下的时域响应,得出如下主要结论:
1) 考虑壁面剪切力与否对液舱晃荡的数值模拟影响不大,壁面条件可选择滑移壁面,同时采用均匀结构网格代替边界加密网格,提高计算效率。
2) 载液量较大时,液舱晃荡力会对船体运动产生明显影响。液舱晃荡力与波浪力相位接近时,将增大船体运动幅度;反之,将减小。对于养殖工船,液舱晃荡力对船体横摇运动影响较大。不考虑液舱晃荡力时,横摇RAO 在波浪频率ω=0.6 rad/s 达到峰值,为0.14 rad/m;考虑液舱晃荡力时,在波浪频率ω=0.5 rad/s 达到最大,为0.20 rad/m,增大了43%。
3) 养殖工船艏、艉不规则舱液量较少,对船体运动影响有限,可将某一波浪频率下,液舱总晃荡力与规则液舱晃荡力的比值视作该比值在所有波浪频率下的值,从而避免计算艏、艉不规则液舱的晃荡。对于规则舱,可用其二维横截面模型代替三维液舱模型,进一步简化计算。
