城轨新线客流成长期进出站量短时预测研究
2020-05-29卢天伟姚恩建刘莎莎周文华
卢天伟, 姚恩建,2, 刘莎莎, 周文华
(1.北京交通大学 交通运输学院,北京 100044;2.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室,北京 100044)
城市轨道交通具有准时、速达、大运量等特性,目前已成为缓解城市交通拥堵的重要方式之一。随着城市轨道交通网络规模的持续扩大,新线不断建设并投入运营,客流变化特征愈加复杂。在此过程中,准确把握新线开通后的进出站客流态势和演变规律,是确保相关部门制定有效运营管理措施、保障新线正常运营的关键。然而,在轨道交通成网运营背景下,新线开通后存在一定时间的客流成长期,在此期间由于乘客对新线的使用习惯尚未固定,新线站点的客流吸引范围和吸引对象尚未稳定,客流处于成长阶段,其变化趋势具有较为明显的增长性和波动性,导致原有针对既有线网的预测模式并不适用,预测结果与实际情况相差甚远。因此,新线客流预测是当前城轨运营管理中亟待研究的问题之一。
目前已有许多城轨新线客流预测相关研究。在全天日客流预测方面,赵路敏等[1]结合线网客流变化的关键因素,提出了利用新线可研和现有站间客流数据来预测新线客流的方法。光志瑞[2]基于站点的土地利用和可达性分析,建立了新线开通初期新站和既有站进出站量预测模型。程涛等[3]基于既有客流的变化规律,根据标定车站客流与土地利用、到离站交通距离与地铁车站选择、合理轨道乘距等数学模型,提出了新线开通初期客运量、断面客流量的预测方法。蔡昌俊等[4]基于刷卡数据统计获得的集计客流数据,依据行为分析理论,建立了新线开通初期城轨站间客流量分布预测模型。姚恩建等[5]使用站点可达性指标定量分析了新线进出站客流的诱增效果,对新线的潜在客流进行了评估。以上研究对象均为日客流,不能够对日内的短时客流变化进行预测。在短时客流预测方面,国内外已有大量针对既有线网客流的预测方法,包括时间序列[6-8]、卡尔曼滤波[9-10]、支持向量机[11-12]、神经网络[13]等方法,但其预测原理均基于历史数据,无法应用于新线短时客流预测。在新线短时客流预测方面,姚恩建等[14]针对新站缺乏历史数据的问题,提出了基于同类既有站匹配的新站历史数据库构建方法,并实现了对新站实时进出站量的预测,但其中并未充分考虑客流变化趋势和预测效率,难以保证预测的有效性和实时性。
综上,现有新线客流预测相关研究主要为全天日客流预测,或新线开通影响下既有站点的客流预测,较少有研究针对新线开通后自身的短时客流进行深入分析,缺少新线客流成长期小粒度、高精度、高效率的进出站量预测方法。然而,新线站点在客流成长期内的进出站量变化不稳定,且缺少历史客流数据,既有的短时客流预测方法无法满足其预测精度和实时计算效率要求,直接影响新线开通后的实时监测与客流评估,导致城轨运营组织不合理的后果。基于此,本文针对新线客流预测缺乏历史数据方面的问题,通过对新线站点进出站客流变化规律的分析,提出基于改进模糊C均值聚类(Fuzzy C-Means,FCM)算法的站点类型划分方法,通过匹配同类既有站点历史数据来对新线站点的历史数据库进行构建;针对预测算法实时性和预测精度方面的问题,基于趋势距离和多元统计回归对K近邻(K-Nearest Neighbor,KNN)算法进行改进,提出新线客流成长期进出站量短时预测方法,以期提高新线进出站量短时预测的计算效率和预测精度,为新线精细化运营管理的强化和改善提供决策支持。
1 新线站点客流成长期进出站量变化规律分析
1.1 新线站点客流成长特征
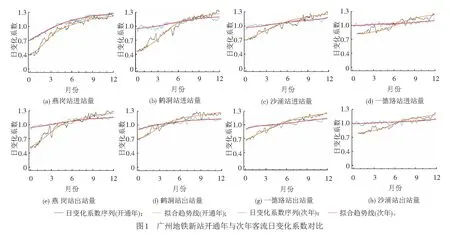
新线站点客流成长期与稳定期的客流变化规律存在较大差异,为探究新线站点的客流成长特征,挑选广州地铁2015年12月28日开通的燕岗、鹤洞、沙涌站以及2015年1月28日初开通的一德路站为例,对新线开通年和次年的进出站客流变化趋势进行对比,各站进出站开通年、次年的客流日变化系数(其值为日客流量与年平均日客流量的比值)及拟合得到的趋势线见图1。由图1可以看出,与次年相比,开通年的客流增长率相对较高、波动性相对较强,该特性也同样存在于其他客流成长期的新线站点,因此新站客流成长期与稳定期客流特征差异性较为明显。
1.2 基于土地利用性质的新线站点客流趋势相似性分析
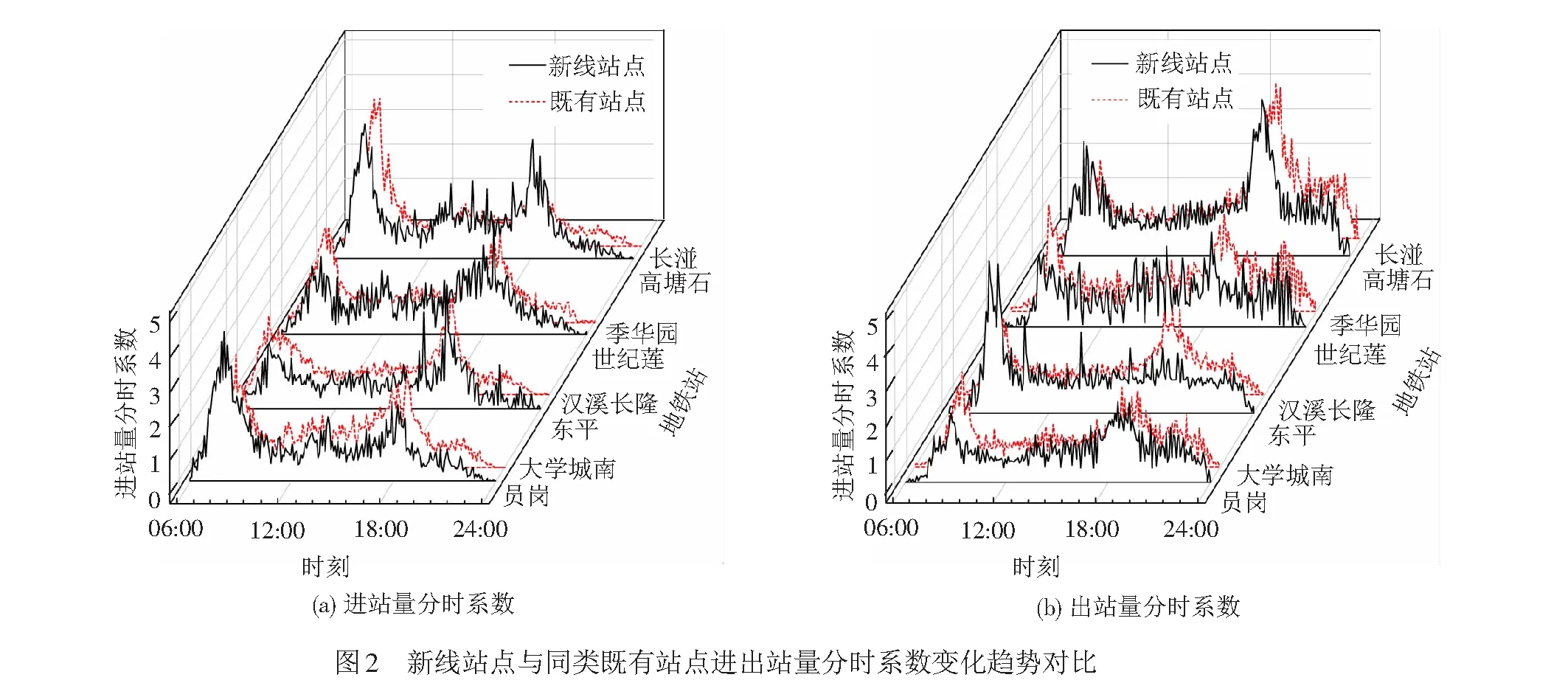
对于土地利用性质相似的站点,其客流变化趋势也具有相似性[15]。以广州地铁进出站客流为例,挑选2017年3月15日(周三)新线站点员岗、东平、世纪莲、高塘石的进出站量数据,与土地利用性质分别匹配的2017年3月8日(周三)既有站点大学城南、汉溪长隆、季华园、长湴的进出站量数据进行比较,二者的进出站量分时系数(各时段实际客流量与是日平均客流量比值)变化趋势对比见图2,可以看出各新站与其匹配的既有站客流变化趋势之间具有较强的相似性。该相似性在图中以外的其他各新站站点与既有站之间也同样存在,因此,针对新线站点客流预测中缺少历史数据的问题,可通过基于趋势相似性的站点类型划分、匹配同类既有站点数据解决。
2 基于站点聚类的新线站点历史数据库构建方法
城轨新线站点客流成长期缺乏历史客流数据作为未来短时进出站量预测的参考依据,使得相关预测方法难以直接应用。基于前文对新线站点与既有站点间客流变化趋势的相似性分析,通过站点类别的划分来分析新线站点与既有站点客流之间的关系,并基于同类既有站点进出站量历史数据来构建新线站点客流预测过程中所需的历史数据库。
2.1 基于改进模糊C均值聚类的站点类型划分方法
基于改进FCM算法对站点类型进行划分,站点短时进出站客流趋势变化特征主要由早高峰、晚高峰、平峰3个时段的进出站量大小决定,因此在聚类指标方面,使用3个时段的进出站量小时系数(其值为小时内客流量与日平均小时客流量的比值)作为趋势变化指标。在聚类算法方面,已有相关研究使用传统FCM算法作为站点分类方法[14]。传统FCM算法能够基于聚类指标的相似度对站点类型进行合理的划分,但其对初始聚类中心敏感,迭代计算目标函数值时容易陷入局部最优解[16],而由于城轨站点分类数、各类别客流特征的不确定性,难以在算法初始确定出较为合理的聚类中心,使用传统FCM算法无法保证最终结果的最优性。因此本文使用一种将启发式思想融入传统FCM的改进算法,该改进算法在传统FCM算法的寻优过程中,每次迭代时使用遗传算法和模拟退火算法中的启发式思想随机更新解集[17],该算法的相关应用研究表明该算法能够使迭代过程跳出局部最优并且加快速度向全局最优解靠近[18-19]。站点类型划分操作流程如下:首先,准备聚类指标数据,并对目标分类数的范围进行确定;其次,使用改进FCM算法对取值范围内的所有分类数进行循环计算,得出所有分类数的站点分类方案;最后,对各分类方案的有效性指标进行计算并比较,确定最优的站点分类方案。
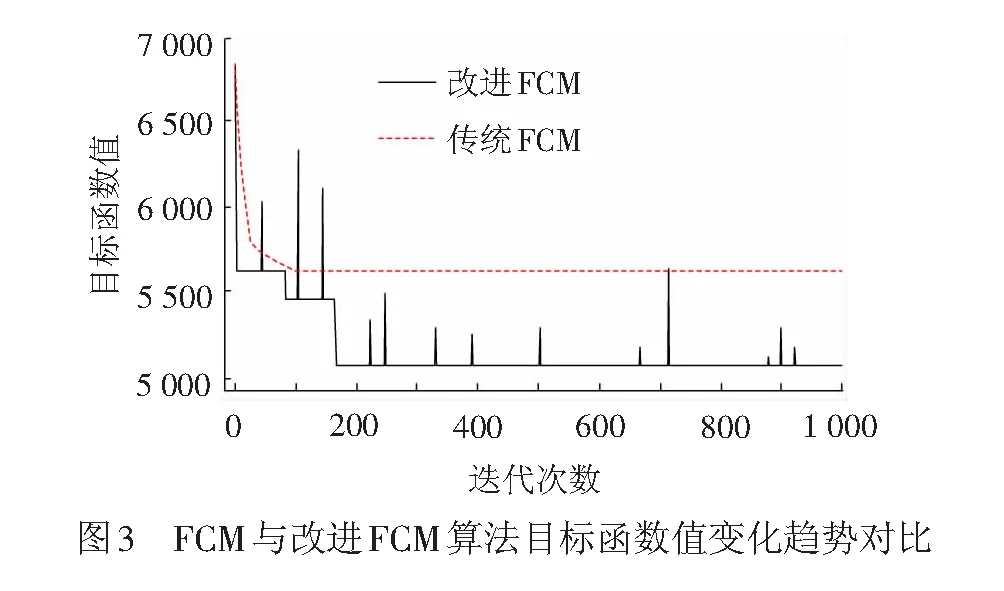
为对站点类型划分方法的改进效果进行分析,以广州地铁为例分别使用传统FCM算法和改进FCM算法进行站点分类,对二者目标函数值的变化进行对比。以2016年10月17日至2016年12月25日期间10个周的工作日历史数据作为数据源、对所有郊区站点进行分类数为4的类型划分为例,其算法寻优过程见图3。其中传统FCM算法在第101次迭代得到了最优目标函数值5 652,之后便一直维持在该数值上;而改进FCM算法通过启发式思想,不断探寻可能存在最优解,在第92、167次迭代时摆脱了局部最优解,最终得到的目标函数值为5 034,提高了最终站点分类方案的最优性。
站点分类方案作为新站历史数据库构建的重要依据,对预测精度有着直接的影响,因此需针对不同分类方案的有效性进行检验和比较,选取最优方案。目前已有的聚类有效性指标(Cluster Validity Index,CVI)中,按其各自特征可分为以下3类:基于数据几何结构的有效性指标、基于隶属度的有效性指标、综合有效性指标[17]。在本文中,由于客流的趋势性因素符合聚类算法中的几何判别特征,而隶属度则能够对不同站点与聚类中心的差异定量化描述,因此为对各分类有效性特征进行较为全面地评判,所选取的有效性指标将涵盖以上3类指标。本文选取的聚类有效性判别指标情况见表1,通过不同站点分类方案之间各指标的比较可对其优劣性进行评判,表中相关性表示有效性指标与聚类有效性的相关性。
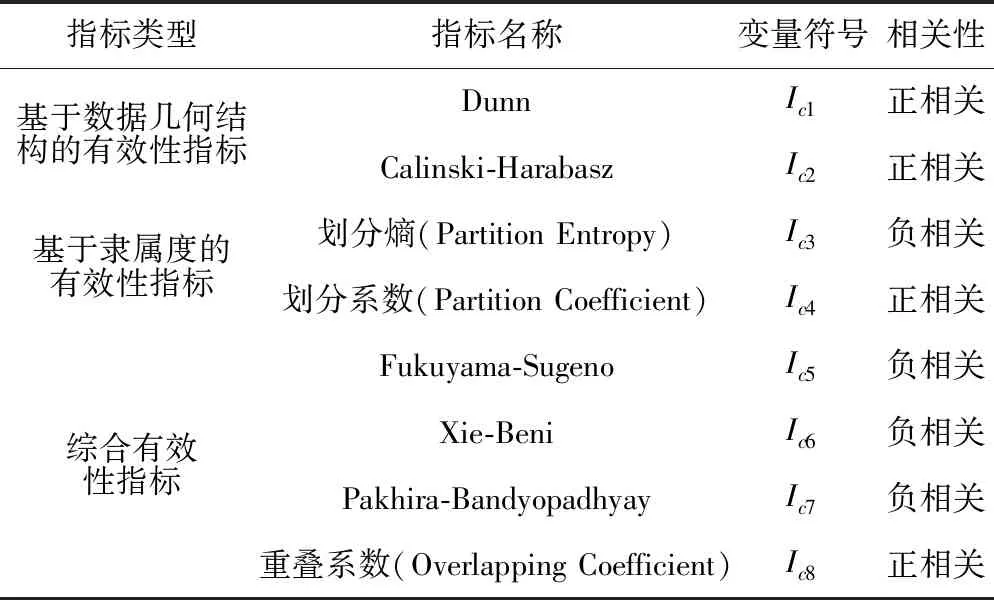
表1 站点分类方案有效性判别指标
上述指标中包含正相关和负相关指标,为直观对比各分类方案的有效性,通过式(1)对各有效性指标进行调整统一和标准化,将所有指标均调整为范围为[0,1]内的负相关指标。
(1)
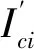
若各指标结果对最优分类方案的判别结果总体一致,则判定该方案为最优方案;否则,对判别结果出现差异的原因进行分析,若分类不合理,则重新选取数据集进行聚类,若差异产生原因合理,则通过计算其加权有效性指标(Weighted Summation type Cluster Validity Index,WSCVI)进一步比较,加权有效性指标为
(2)
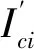
对于新线站点而言,由于其客流成长期间历史数据较少,对其站点类型进行确定时需要首先对其站点周边土地利用情况、可行性研究报告进行评估,从而将该新线站点归到土地利用性质相近的站点类别中,实现对新线站点类型的确定。
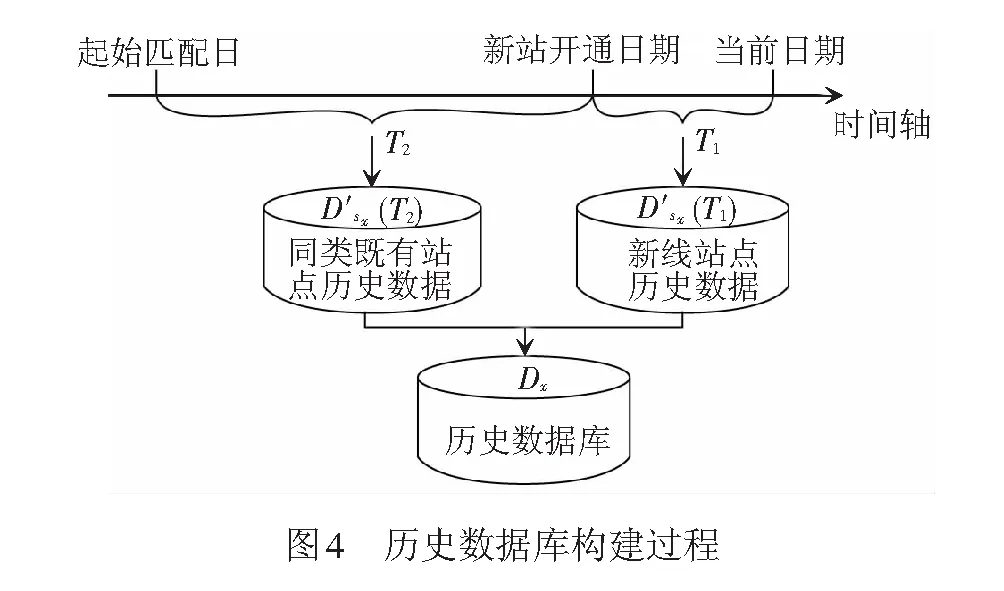
2.2 历史数据库的构建
由于新线站点的历史数据较少,无法构建其进出站客流短时预测过程中所需完整的历史数据库,难以保证预测结果的精度。针对这一问题,提出新线站点的历史数据库构建方法,一方面,将既有的少量新线站点历史数据加入历史数据库;另一方面,基于前文所得的站点分类方案,根据新线站点和同类既有站点的站点类型进行匹配,将同类站点的历史数据作为新站的历史数据,构建新线站点进出站量预测所需的历史数据库。具体构建方法如下。
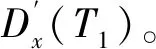
其次,建立新线站点与既有站点之间的匹配关系,以描述新线站点的预测日期类型、位置类型、站点类型与既有站点的映射关系。对于新线站点x,有
Sx=f(U,Lx,Cx)
(3)
式中:Sx为新线站点x匹配得到的相似既有站点集;U为预测日期类型(周次);Lx为新线站点x的位置类型(市区、郊区);Cx为新线站点x的站点类型。
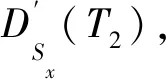
(4)
3 基于改进K近邻算法的新线站点客流成长期进出站量短时预测方法
城轨新线站点客流成长期内短时进出站量存在不同幅度的波动,且缺乏历史数据的支撑,即使可参考同类既有站点的历史数据,但若没有合理的匹配机制和预测算法,则无法保证预测效率和精度。
KNN算法作为一种非参数回归方法,能够针对给定测试实例,基于距离度量找出训练集中与其最靠近的K个实例点,并基于K个最近邻的信息来进行预测。目前,已有研究提出基于KNN算法的短时交通流预测方法[14],该算法能够基于当日实际发生的时段客流数据特征来确定状态向量,寻找与预测目标相匹配的K个历史日客流数据作为K近邻数据,并将其作为预测算法的输入,实现对目标时段客流的预测。但由于其历史数据库中数据量庞大,既有算法中近邻匹配步骤耗时较长,计算效率有待提高;在预测原理方面完全基于历史数据,没有充分考虑历史数据与预测目标之间的差异性,且没有考虑未知因素对短时客流的影响,其预测精度有待增加。
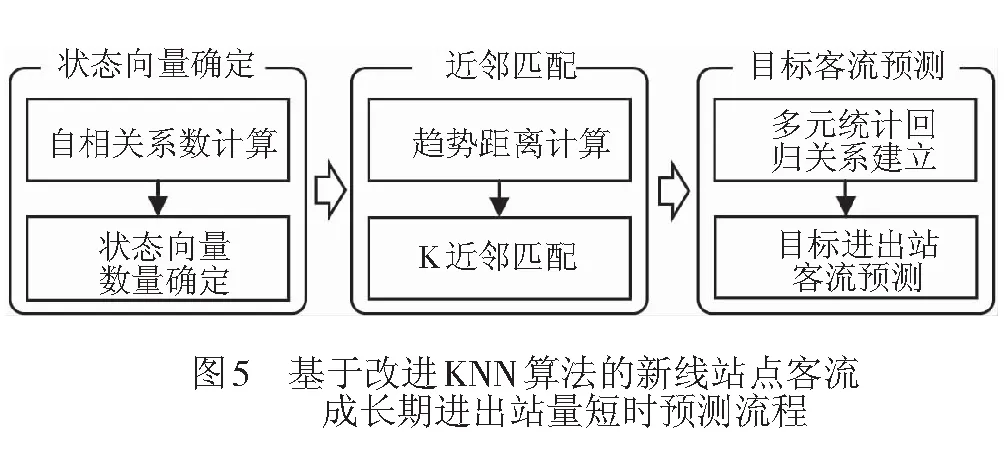
本部分预测方法主要分为状态向量确定、近邻匹配、目标客流预测3个步骤,见图5。其中,在近邻匹配机制中,提出趋势距离的概念和计算方法,用以提高既有机制的匹配效率;在目标客流预测过程中,结合多元统计回归原理,消除预测目标与近邻数据之间的差异性,改进传统KNN算法,以期进一步提高预测精度。
3.1 状态向量的确定
各时段的短时客流均可看作独立的时间序列,在各序列中连续若干时段的客流数据间具有较强的相关性,因此选取与目标预测时段客流相关性最强的若干相邻时段客流作为状态向量。时段个数m可通过计算q阶自相关系数rq来确定,计算式为
(5)
(6)
对于给定的自相关系数阈值M,当rq≥M时,可认为时间序列中间隔q个时段的2个值相关性较强。为使状态向量中尽多地包含与预测时段相关的客流时段,取m=max{q|rq≥M},并由预测时段前m个时段客流构成状态向量。
3.2 基于趋势距离的近邻匹配机制
目前大多数研究通常使用欧式距离来衡量预测目标与历史数据之间的匹配度,但由于历史数据库中数据量较为庞大,在实际短时客流预测中的近邻匹配计算过程会耗费大部分时间,难以保证预测结果的时效性。而本文中对于近邻的确定仅需对各近邻与预测目标的距离进行比较,不需其具体距离值具有很高的精确度。因此,为了节约近邻匹配的搜索时间,本文提出趋势距离的概念和计算方法,用以替代欧式距离作为近邻匹配机制的判定指标。趋势距离的计算方法为
(7)
Suv=|P0v-Puv|
(8)
式中:Su为预测目标与第u个近邻数据之间的趋势距离;Suv为预测目标与第u个近邻历史数据之间第v时段进出站量的趋势差;P0v、Puv分别为预测目标、历史数据的进出站量分时系数。
在计算效率方面,趋势距离的乘除法计算量仅为1,而欧式距离的乘除法计算量为m+1,对于每次预测流程中的近邻匹配步骤而言,需计算的近邻数量为m(T1+T2)。因此,与欧式距离相比,趋势距离的使用够在保证匹配精度的前提下,减少m2(T1+T2)的乘除法计算量,大幅度提高计算效率。
对于近邻数K的确定,目前大多数研究通过对不同K值下的样本测试结果进行误差比较,取最优作为K的固定值。为消除不同变化特征的进出站客流匹配偏差,本文在预测过程中将实时动态计算不同时段对应K值,并采用交叉验证法来确定最优K值。
3.3 基于多元统计回归的改进算法
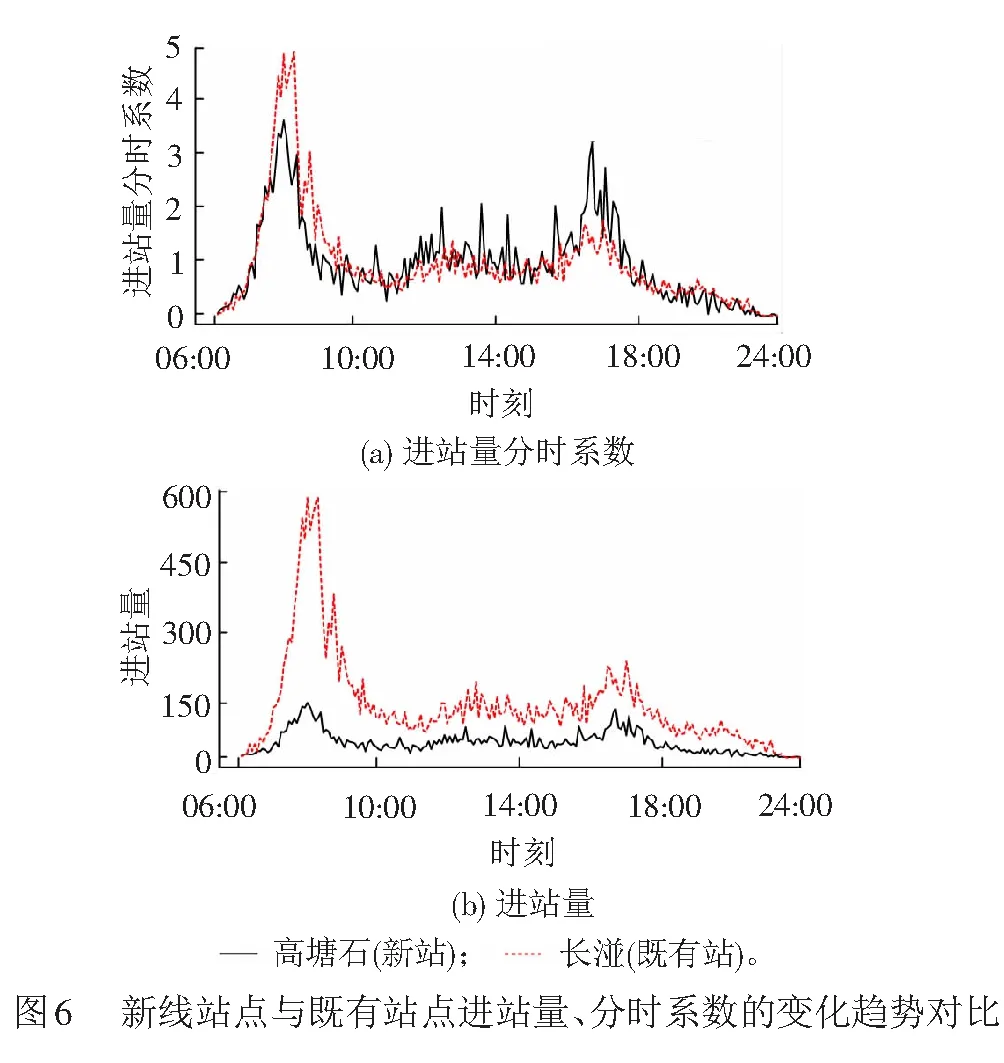
针对基于K近邻的预测算法,目前通常的方式为对近邻数据依据时间序列加权平均来计算预测值[20]。然而,本文站点类型划分时采用的指标为客流分时系数而非客流量,对于新线站点而言,虽与同类站点在客流变化趋势上具有相似性,但无法保证具体客流大小一致。以2017年3月15日(周三)的新线站点长湴站以及其2017年3月8日(周三)同类既有站点高塘石的进站客流为例,新线站点与既有站点进站量分时系数的变化趋势对比见图6,由图6可见,二者的进站量分时系数虽一致性较强,但进站量之间的差异却很大。因此若直接使用同类既有站点的数据进行简单平均计算进行预测,会造成较大的预测偏差。
针对上述问题,本部分将多元统计回归应用于KNN算法中,定量刻画预测目标与近邻数据之间关系。在预测效率方面,多元统计回归对比其他预测方法具有较高的计算效率,对短时客流预测的时效性影响较小;在预测原理方面,多元统计回归能够通过回归参数的估计来确定不同近邻的权重系数,建立预测目标与近邻数据之间的关系,消除二者之间的差异性。因此,本部分在传统KNN算法的基础上结合多元统计回归的特点提出改进预测算法。具体改进方法为:针对状态向量中的元素,以K个近邻对应的数据作为自变量,目标预测日对应的数据作为因变量,建立多元统计回归关系,并进行参数估计。多元统计回归关系为
Q(i)=Q·a+b+ε
(9)
Q=[Q1(i),Q2(i),…,QK(i)]
(10)
a=(a1,a2,…,aK)T
(11)
式中:Q(i)为预测日第i时段的进、出站量;Q为各近邻第i时段进出站量组成的向量;a为各近邻回归参数组成的向量;b为常数项;ε为随机误差项。
4 案例分析
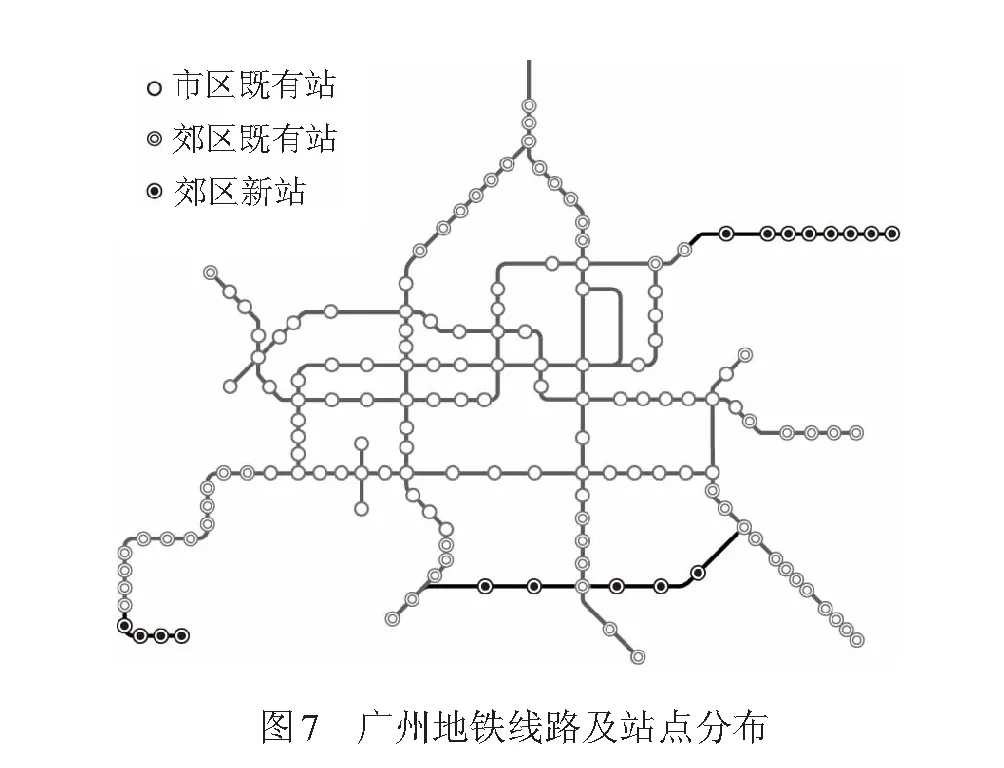
以广州地铁2017年开通新线站点的5 min粒度进出站客流为例,对预测方法的有效性进行检验。广州地铁于2016年12月28日开通了6号线二期、7号线一期和广佛线二期共17个新站,截至2017年6月27日,全网共157个站点,具体线路和站点分布见图7。根据预测日期类型和站点位置类型,可将站点客流为工作日市区、周六日市区、工作日郊区、周六日郊区4类。由于此次新开通站点均为郊区站点,本部分将以工作日郊区为例进行分析,其中包括既有站点59个,新线站点17个。根据相关方法对本例中各新线站点客流成长期的界定,其客流成长期跨度均在3个月以内,因此,将2016年12月28日至2017年3月31日之间的日期作为目标预测日期,并将预测结果与实际数据进行对比,来对预测方法的精度进行检验。
4.1 站点类型的确定
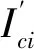
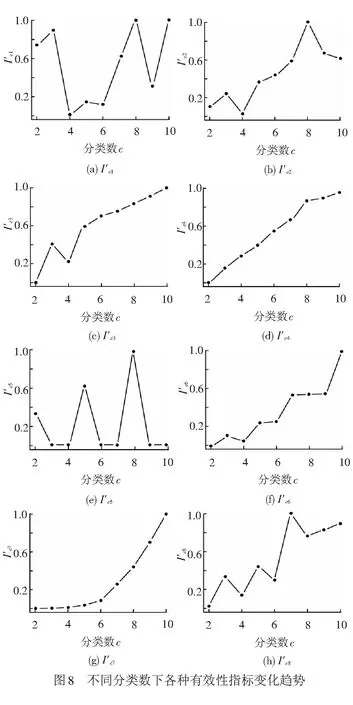
为进一步对最佳分类方案进行判定,接下来对各分类方案的加权有效性指标Ic进行计算,取所有权重系数均相等、判别阈值IT=0.2,各分类方案的Ir计算结果见表2。可以看出,I4=0.09为最小值,因此c=4为最佳分类数。
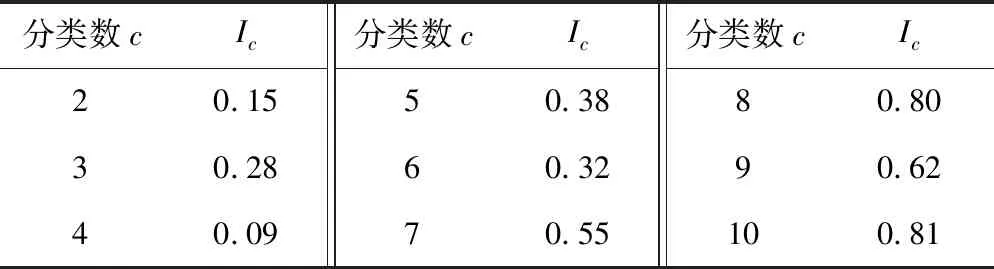
表2 各站点分类方案的加权有效性指标Ic
该分类方案的聚类中心见表3,依据聚类中心中的各指标特点可将各类型依次定义为居住类、办公类、枢纽类、综合类。其中,居住类早高峰进站、晚高峰出站系数较大,办公类早高峰出站、晚高峰进站系数较大,枢纽类各系数均处于较高水平,综合类系数无明显特征。
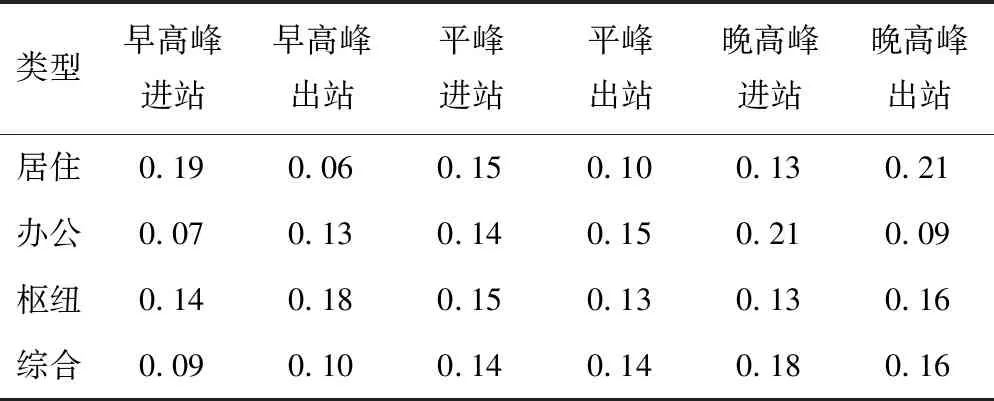
表3 工作日郊区站点聚类中心(小时系数)
对于本例中的新线站点,根据周边土地利用情况、可行性研究报告确定其工作日的站点类型,见表4。

表4 工作日郊区新线站点分类情况
4.2 客流预测及精度分析
选取2016年12月28日至2017年3月31日期间所有工作日作为目标预测日,对预测方法的各个步骤进行实现。首先对17个新线站点的工作日历史数据库进行构建,由于本案例中既有站点数据量充足,且站点的同周次进出站客流变化规律相似,本部分将对每个新站周一至周五5个周次分别构建历史数据库。
通过对所有目标预测过程的执行,统计结果显示,进、出站客流短时预测的平均执行时间分别为29.12、26.84 s,同等计算机配置下的传统KNN方法平均执行时间为45.28、39.61 s,计算效率较传统KNN方法分别增加了35.68%、32.23%。
对于预测方法精度,本文采用平均绝对误差EMAE和平均绝对百分比误差EMAPE对其进行检验,定义为
(12)
EMAPE=1/T×
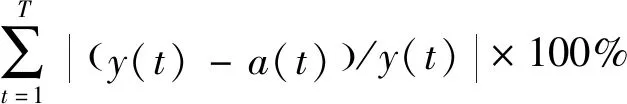
(13)
式中:t为5 min粒度预测时段;T为总预测时段个数;y(t)为时段t进(出)站量真实值;a(t)为时段t进(出)站量预测值。
预测结果见表5。
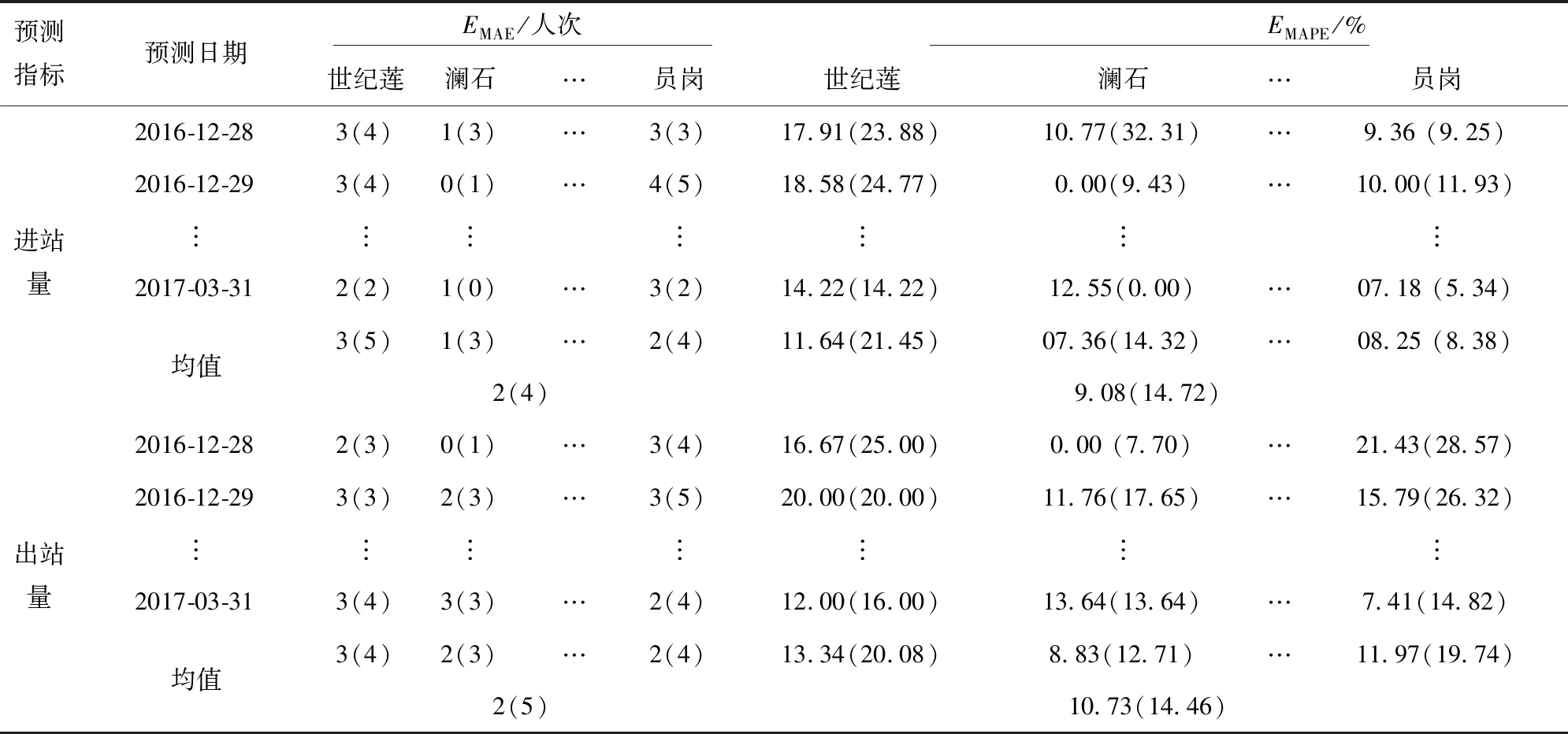
表5 广州地铁2016年12月28日至2017年3月31日期间新线站点工作日5 min粒度进出站客流平均预测误差
注:括号外数值为使用本文方法进行预测的误差结果;括号内数值为使用传统KNN方法进行预测的误差结果。
根据误差统计结果可知,绝大部分EMAPE均在20%以下,少数在20%以上,这是由于郊区新线站点的5 min进出站客流较小,较小的EMAE变动就会带来较大的EMAPE变化。EMAE均值仅为2人次说明预测误差较小,属于可接受范围。通过与传统KNN方法预测误差的对比可以发现,绝大部分的MAE和MAPE均有所降低。改进方法的进、出站量EMAPE均值分别为9.08%、10.73%,传统方法的进、出站量EMAPE均值分别为14.72%、14.46%,改进算法对于进、出站量的预测精度较传统算法分别增加了38.32%、25.80%。
不同类型站点客流平均预测误差的统计结果见表6,对比传统算法EMAE和EMAPE的平均值,改进算法中不同站点类型的预测误差均有所降低且处于较低水平,表明改进算法针对不同类型的站点均有较好的预测精度。
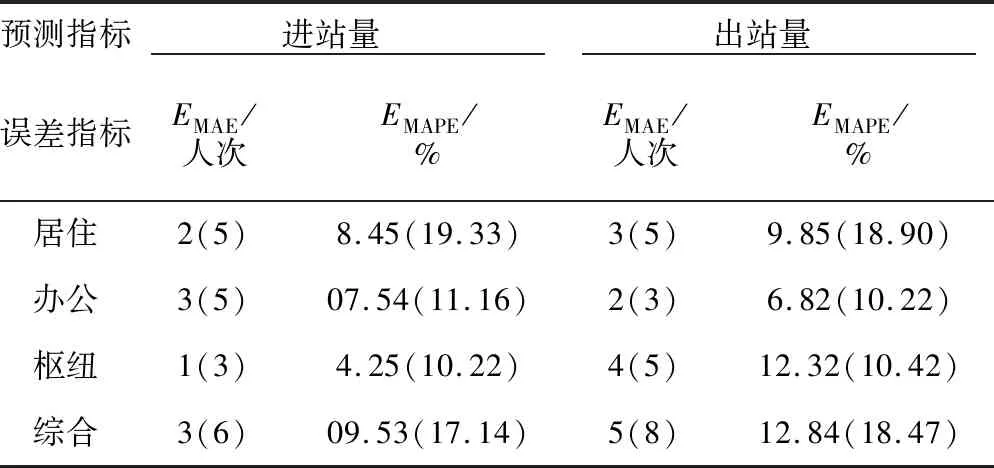
表6 广州地铁2016年12月28日至2017年3月31日期间不同类型新线站点5 min粒度进出站客流平均预测误差
注:括号外数值为使用本文方法进行预测的误差结果,括号内数值为使用传统KNN方法进行预测的误差结果。
5 结论
本文基于改进FCM算法和改进KNN算法提出了城轨新线客流成长期进出站量短时预测方法,并以广州地铁为例对方法的有效性进行了评价,得出以下结论:
(1) 结合城轨站点短时进出站客流变化的趋势相似性,基于改进FCM算法对站点类型进行了划分,并提出了新线站点的历史数据库构建方法。对比传统FCM算法,该方法能够有效解决算法陷入局部最优的问题,得出更优的站点分类方案和新线站点历史数据库。
(2) 基于趋势距离对新线站点与既有站点之间的数据匹配机制进行了优化。对比传统匹配机制,该匹配机制能够显著减少近邻匹配过程的计算量,增加算法的总体计算效率,提高实际运营过程管理中新线进出量短时预测的时效性。
(3) 基于多元统计回归对KNN算法进行了改进,提出了城轨新线客流成长期进出站量短时预测方法。改进KNN算法能够量化预测过程中的预测目标与近邻数据二者之间的局部线性关系,消除二者之间的差异性,提高新线进出站量的短时预测精度。
