节流孔出气模式对静压干气密封稳态性能影响
2020-05-28车健江锦波李纪云彭旭东马艺王玉明
车健,江锦波,李纪云,彭旭东,马艺,王玉明
(浙江工业大学过程装备及其再制造教育部工程研究中心,浙江杭州310014)
引 言
小孔节流静压干气密封是一种新型的非接触式轴端密封,通过外部供气或密封腔引气等方式将一定的带压气体通过节流结构进入密封端面,从而形成可观的流体静压承载力,使干气密封在静压或低速条件下形成稳定气膜。相较于经典螺旋槽干气密封,其在低速条件下具有更大承载力和气膜稳定性,因而在制药釜、搅拌器等低速旋转设备中得到应用[1-2]。
自加压式静压干气密封由Cheng 等[3]在1967 年所提出,并对比分析了小孔节流静压密封、雷列台阶静压密封和螺旋槽端面密封的压力分布和静态稳定性;Stolarski 等[4]考虑粗糙度的影响,分析了密封环变形、压力和速度对静压干气密封稳态性能的影响。不过近几十年来国外关于静压干气密封的研究较少,国内关于静压型和动静压干气密封的研究主要集中于采用不同数值方法求解雷诺方程或N-S 方程以获得静压干气密封膜压分布,进而分析节流结构参数和工况参数对静压干气密封稳动态特性的影响。许恒杰等[5-6]和管羽刚等[7]采用解析法求解静压干气密封的稳态性能,并分析了节流孔直径、个数、介质压力和节流气压力等参数对其稳态性能的影响规律;李双喜等[8-9]采用Fluent 软件对动静压型干气密封的端面流场和压力场开展数值模拟,探讨了不同工作状态下动静压干气密封的密封性能;李双喜等[10-11]和刘雨川等[12]基于有限元法求解雷诺方程或N-S 方程以获得静压或动静压型干气密封端面膜压分布和稳态性能,进而探讨了结构和工况参数的影响;赵艳凤等[13]采用有限差分法求解雷诺方程以获得膜压分布,并探讨了均压槽形状对静压干气密封稳态性能影响。基于小扰动法,许恒杰等[14]和张树强等[15]、尹源等[16]分别采用有限差分法和有限元法求解微扰雷诺方程,分析了多自由度扰动下静压干气密封的动态特性。
值得注意的是,小孔节流静压气体轴承中的实验研究发现[17-18]节流气进入密封间隙后,会在节流孔出口附近形成明显涡流和压力波动,进而引起气膜压力的迅速下降和逐渐回升现象,而这种压力的突降和回升会对气体轴承的承载力和耗气量产生影响,目前在静压干气密封研究中所用的解析法或基于有限差分法和有限元法求解雷诺方程的方法无法准确描述这一现象,故有待从静压气体轴承研究中借鉴对静压气体润滑压力分布描述更准确的分析方法。另一方面,目前关注较多的是通过节流孔、均压槽形状及尺寸参数优化或气膜厚度调控以提高静压干气密封的气膜承载力和气膜刚度,而关于节流孔分布及出气模式对静压干气密封性能的影响及提升机制则未见探讨。
本文首先采用湍流大涡模拟方法,分析了节流孔位置和气膜厚度对单列孔节流静压干气密封稳态性能的影响规律,探讨了径向单列节流静压干气密封的性能局限性;随后对比分析了不同出气模式的径向多列节流静压干气密封稳态性能,在不同运行膜厚下获得了最佳的出气模式匹配。在此基础上,提出了一种出气模式可调的静压干气密封结构,并通过外部调控出气模式以实现静压干气密封的高气膜承载、低泄漏率和低耗气量的目标。
1 分析模型
1.1 几何模型
节流孔和均压槽是小孔节流静压干气密封中关键的节流结构。图1所示为经典小孔节流静压干气密封及其开孔端面几何结构示意图。静压干气密封的主要结构为由静环和动环组成的一对密封副,在静环端面径向中部开设有径向宽度为w、深度为hd的环形均压槽,在均压槽内周向均匀分布有数量为N、直径为d、轴向长度为l的节流孔。密封端面的外半径、内半径和均压槽中心半径分别为ro、ri和re。在静压干气密封运行时,压力为ps的缓冲气经节流孔节流降压后进入到环形均压槽内,随后一部分气体通过厚度为h的密封间隙进入到密封端面内径侧而形成内泄漏qi;因节流气压力高于外径压力,另一部分气体进入到密封端面外径侧而形成外泄漏qo,内、外泄漏量之和为耗气量q。
1.2 控制模型
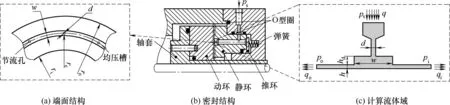
图1 静压干气密封几何结构图Fig.1 Geometric structure of hydrostatic dry gas seal
由于静压DGS 气膜厚度仅仅为几微米,从实验角度得到流场内部气体流动较为困难,目前经常使用流体计算力学(CFD)数值模拟方法,对密封端面开启力和泄漏率等性能参数进行分析和计算。在节流孔出口区域,高速的缓冲气进入到密封端面会形成复杂的湍流流场,这时就需要求解完整的N-S方程来解析流场中微小的流动情况[19-20]。大涡模拟(LES)数值计算目前已广泛应用于瞬态流场计算,该方法通过湍流运动的过滤将湍流分解为大尺度脉动和小尺度脉动,大尺度量通过数值求解滤波后的Navier-Stokes 方程获得,小尺度的脉动可采用亚格子模型求解[21]。由于大尺度脉动是直接数值求解,而边界条件又对小尺度脉动影响较小,故大涡模拟方法可适用于复杂湍流流动的模拟。利用密度加权滤波器(Favre 方法)对可压缩Navier-Stokes 方程滤波得到连续性方程、动量方程和能量方程,对其联立求解。需要注意的是,其中的亚格子应力项不能通过微分方程求解,可采用Smagorinsky-Lilly 亚格子雷诺应力模型对其求解,使方程组封闭。
采用大涡模拟求得静压干气密封气膜压力分布后,对其在密封端面上积分可获得密封开启力F,进一步可获得气膜刚度kz。内、外径泄漏率为计算域气膜内、外径过流面积的体积流量;耗气量为内外泄漏率之和,具体表达式如下
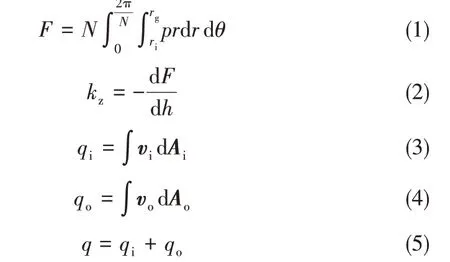
式中,p 为密封端面任意点的压力分布,vi和vo分别为密封端面内径ri和外径ro处的气体流速,规定流出计算域的流速为正。Ai和Ao分别为密封端面内径ri和外径ro处的环形泄漏面积,其中Ai=2πrih,Ao=2πroh。规定指向流体流出计算域的方向为正,不考虑温度对密封端面影响。需要指出的是,上述公式中q、qi和qo为标准大气压且温度为293 K 条件下的体积流量。
1.3 建模及仿真设置
图2 所示为静压干气密封计算流体域ICEM 网格划分。为缩短计算时间,考虑到密封端面节流结构的周向对称性,可取全周期的1/N 作为计算流体域。先利用Fluent 前处理器ICEM 对静压干气密封中包括节流孔、均压槽和密封气膜三部分在内的流体域进行网格划分,采用高精度的结构化网格,其中节流孔和均压槽、均压槽和气膜两处交界区域进行局部网格加密。

图2 静压干气密封计算流体域网格划分Fig.2 Grid meshing of computing domain of hydrostatic dry gas seal
采用Fluent湍流大涡模拟来计算静压干气密封的膜压分布和稳态性能。具体计算过程为:首先选用以单个节流孔为中心且左右径向边界呈30°夹角的流体计算域为计算模型,给定工况和密封环几何参数,采用三维双精度求解器,选择基于压力求解的湍流大涡模拟模型进行瞬态计算,其中亚格子模型选择Smagorinsky-Lilly[22];在气体的物性参数方面选择可压缩理想气体,动力黏度µ满足Sutherland方程
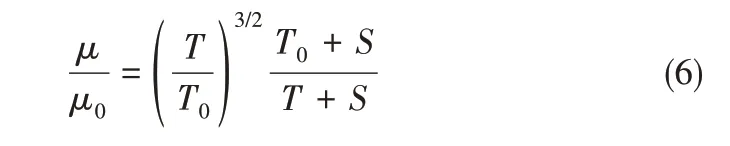
其 中,µ0=1.716×10-5Pa·s,S=110.55 K,T0=273.11 K。
采用强制性压力边界条件,包括内径压力pi,外径侧压力po,节流气压力ps,以及左右两边的周期边界;压力速度耦合采用SIMPLE 算法,利用二阶迎风插值格式来减小密度、湍流动能和耗散等,动量采用边界中心差分格式;监测密封端面膜压平均值p,根据收敛条件,调整松弛因子,计算时间步长为0.01 ms,单个时间步长内迭代500次。
2 结果讨论与分析
借鉴静压轴承领域[23-27]对于节流结构参数的选择,给定本文计算模型的几何参数,如表1所示。未做特别说明,下文的数值计算中均采用表1 中所示的计算参数。本次计算模型中基于以下假设:(1)假设流体为可压缩理想气体;(2)流体在界面上无相对滑动,即贴于表面的流体流速与表面速度相同;(3)忽略密封端面变形及介质温度变化的影响。

表1 静压干气密封初始计算参数Table 1 Initial calculation parameters of hydrostatic dry gas seal
2.1 网格无关性与程序正确性验证
为验证所选用湍流大涡模拟计算模型和方法的正确性,将其与静压气体轴承径向压力分布的雷诺方程数值计算结果和实验测试结果进行对比[28],如图3 所示。从图中可看出,高速缓冲气流出节流孔后,压力迅速降低,在节流孔出口附近会形成局部压降现象,随后压力逐渐回升至某一稳定值。基于层流假设的经典雷诺方程计算所得的气膜压力在节流孔出口附近并不会出现明显的压力下降和回升区域,且压力明显高于试验测试结果;而在整个径向范围内,基于湍流大涡模拟方法计算所得的气膜压力分布与试验测试结果基本吻合,从而证明该方法在求解静压气体润滑问题的可行性和正确性。

图3 不同数值模拟方法所得气膜压力分布与实测值对比Fig.3 Film pressure obtained by different numerical simulation methods and measured values
由此可见,与以往基于解析法或采用有限元法、有限差分法求解基于层流假设的雷诺方程以获得静压干气密封稳态性能相比,采用湍流大涡模拟方法能更准确地求解出静压干气密封节流孔出口附近的气膜压力分布,从而使密封开启力、气膜刚度和泄漏率等稳态性能参数数值预测精度更高。
为选取合适的网格数量,以兼顾计算精度和计算时间,本文计算了密封开启力随网格数量的变化规律,如图4 所示。从图中可看出,随着网格数从48.6 万增加至149.8 万,密封开启力先迅速减小,当网格数超过100 万后趋于平缓,故下文数值计算时选取的网格数量为100万。

图4 网格无关性验证Fig.4 Grid independence verification
2.2 径向单列节流孔静压干气密封的性能分析
在小孔节流静压气体轴承的研究中发现[29-31],节流气压力的适当提高有助于使静压润滑气膜的承载力和气膜刚度得到提升,但过大的节流气压力容易造成静压气体轴承或密封气膜的气锤自振,从而使其动力失稳而失效,故本节主要探讨气膜厚度和节流孔径向位置对单列节流静压干气密封稳态性能的影响。
图5所示为经典小孔节流静压干气密封的开启力F、气膜刚度kz、内泄漏率qi、外泄漏率qo和耗气量q 等稳态性能参数随气膜厚度的变化规律。从图中可看出,随着气膜厚度的增大,静压干气密封的开启力单调递减,而气膜刚度呈现出先增大后减小的变化规律,当膜厚为8 μm 时达到最大值,这与常规螺旋槽干气密封的气膜刚度随膜厚增加而单调递减的规律有明显区别,说明静压干气密封只有在合适的运行膜厚下才能获得最大的气膜刚度;密封内泄漏率呈增速递增的变化规律,外泄漏率则先增大后减小,而耗气量则先迅速增加后趋于稳定值。这是因为随着气膜厚度的增大,节流孔处的压力峰值迅速减小,一方面膜厚的增大会引起内、外泄漏的迅速增加,另一方面因节流孔处压力与内、外径压力之间的压差减小则会使得内、外泄漏减小,因节流孔处压力与外径压力之间的压差更小,这种对气体泄漏的削弱作用在节流孔与端面外径之间的上游区尤为明显,这两种作用共同决定了干气密封的内、外泄漏率及供气量。特别地,当节流孔处的压力低于外径侧压力时,静压干气密封的外泄漏率呈现为负值,也即介质由外径侧向内径侧流动。
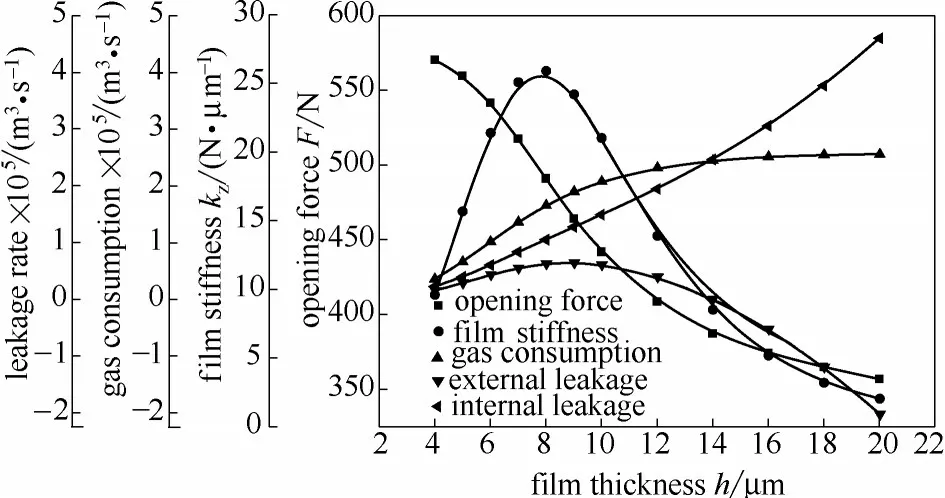
图5 经典小孔节流静压干气密封稳态性能参数随气膜厚度变化规律Fig.5 Influence of film thickness on steady-state performance of hydrostatic dry gas seal with normal orifice-type restrictor
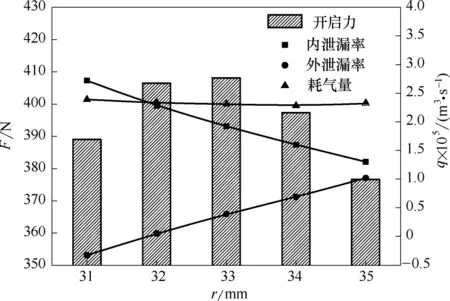
图6 节流孔径向位置对静压干气密封稳态性能影响Fig.6 Influence of orifice radial position on steady-state performance of hydrostatic dry gas seal
图6所示为节流孔径向位置对静压干气密封开启力、泄漏率和耗气量的影响。随着节流孔中心所在半径的增大,也即节流孔逐渐从内径侧向外径侧移动,静压干气密封的开启力呈现出先增大后减小的变化规律,其中在r=33 mm时达到最大值,也即当节流孔开设在密封端面径向中部时具有最大的气膜承载力;内泄漏率呈线性递减,外泄漏率呈线性递增,而耗气量则基本不变,这是因为随着节流孔逐渐向外径侧靠近而远离内径侧,节流缓冲气向内径泄漏的流阻增加,而向外径侧泄漏的流阻减小,不过总的流阻基本不变,故耗气量基本不受节流孔径向位置影响。值得注意的是,当节流孔非常靠近内径侧时,节流缓冲气的外泄漏率为负值,也即上游区的密封气体由外径侧向内径侧流动。
2.3 径向多列节流孔静压干气密封稳态性能
从上述的分析中可以看出,相对于径向单列节流孔静压干气密封而言,单纯依靠选择合适的运行膜厚和优化节流孔径向位置虽然能在一定程度上提高静压干气密封的气膜承载力和刚度,但是效果有限。研究采用径向多列节流孔同时供气静压干气密封结构的气膜润滑性和密封性,并通过出气模式匹配和径向各列节流孔周向位置的优化以更好地平衡静压干气密封的气膜承载力、刚度和密封性。
图7所示为径向多列节流孔静压干气密封的端面结构和计算域示意图。对于径向各列节流结构,其都由宽度为w的环形均压槽和数量为N 的节流孔组成,且各节流结构沿径向均匀布置。从外径至内径侧,节流孔中心处的半径r1、r2和r3分别为34.75、33和31.25 mm,各列节流孔直径和均压槽宽度相等,分别为d=0.2 mm 和w=1 mm。引入逻辑变量——出气模式I 以表示径向各列节流孔的供气模式,I 的位数与节流孔径向列数相等,某位上的数值0 表示给定径向位置未开设节流结构,1 则表示给定径向位置开设周向12 个节流孔以及环形均压槽,I 的第1、第2和第3位分别对应靠近外径侧、径向中间位置和靠近内径侧的节流结构供气情况,如I=010 表示仅有径向中间位置供气的供气模式,I=101 则表示靠近外径侧和靠近内径侧的两列节流孔同时供气的供气模式。

图7 径向多列节流孔静压干气密封端面结构示意图Fig.7 Geometric structure of hydrostatic dry gas seal surface with multi-row orifices
图8所示为四种不同出气模式的多列节流孔静压DGS 与经典单列节流静压DGS 的开启力、泄漏率和耗气量。从图中可看出,与单列节流静压DGS(I=010)相比,多列节流静压DGS 的开启力、泄漏率和耗气量都有所增加。开启力和耗气量主要受节流孔列数影响,相较于经典单列节流静压DGS,双列节流静压DGS 的开启力和耗气量增幅分别约为10%和85%,三列节流静压DGS 的开启力和耗气量增幅分别约为20%和150%。从最关键的开启力和内泄漏率两个指标来看,相较于I=010 出气模式,I=110 出气模式在使开启力增幅达到10%的前提下内泄漏率增幅控制在15%,而其他出气模式的内泄漏率增幅都在50%以上。

图8 不同出气模式静压干气密封开启力与泄漏率Fig.8 Effect of exhaust mode on opening force and leakage rate of hydrostatic dry gas seal

图9 不同出气模式下静压干气密封径向压力分布Fig.9 Radial pressure distribution of hydrostatic dry gas seal with different exhaust mode
图9所示为四种径向多列节流静压DGS与经典单列节流静压DGS(I=010)的径向膜压分布。从图中可看出,I=111 出气模式在整个密封端面径向范围内具有最大的膜压值,故而形成最大的气膜承载力和耗气量。出气模式I=110 和I=011 分别在经典出气模式I=010 结构基础上增加了靠近外径侧节流供气和靠近内径侧节流供气,故其分别能在靠近外径侧和靠近内径侧区域形成明显的压力峰值,从而引起开启力和耗气量增加,不过I=110 对外泄漏率影响较大,而I=011对内泄漏率影响较大。

图10 不同出气模式静压干气密封稳态性能参数随膜厚变化规律Fig.10 Effect of exhaust mode on steady-state performance of hydrostatic dry gas seal under different film thickness
上述分析是在给定气膜厚度h=12 μm条件下获得的。实际上,静压干气密封可能会在不同的气膜厚度下运行,且气膜厚度可通过改变节流气压力或闭合力的方式以调控,故有必要获得不同气膜厚度下各径向多列节流出气模式静压干气密封的运行性能。图10所示为四种多列节流出气模式与I=010的经典单列节流出气模式静压DGS 的开启力、气膜刚度、内泄漏率和耗气量。在各给定膜厚条件下,I=111 出气模式静压DGS 的开启力、内泄漏率和耗气量最大,而I=010 出气模式静压DGS 最小。当气膜厚度h<10 μm 时,I=101 出气模式静压DGS 具有最大的气膜刚度,且较其他几种出气模式静压DGS 高出25%以上;而其他三种径向多列节流静压DGS 的气膜刚度最大值与I=010 出气模式相比并无明显优势,可见I=101 出气模式适用于膜厚较小的场合。当h>10 μm 时,I=111 出气模式具有最大的气膜刚度,而其他三种径向双列节流静压DGS 的气膜刚度差异不大。考虑到I=110 出气模式仅比I=010 出气模式的内泄漏率高出10%,而较其他三种径向多列节流静压DGS要低20%~50%,故在膜厚较大时宜选用I=110 出气模式的静压DGS。耗气量主要受节流孔径向列数影响,而与出气模式关联较弱,相较于经典的I=010 出气模式静压DGS,径向双列节流静压DGS 的耗气量增幅为60%~100%,而径向三列节流静压DGS的增幅为120%~180%。由此可见,不同出气模式的静压DGS 在不同运行膜厚下的性能各异,有望通过出气模式的合理选择以满足不同运行膜厚和工况条件下静压干气密封的低泄漏、高承载和高刚度的性能需求。
2.4 新型出气模式可调静压干气密封性能分析
鉴于径向多列节流静压干气密封对不同运行工况更强的适应能力,并借鉴淋浴喷头出水模式可调原理,提出一种新型出气模式可调静压干气密封结构,以期通过调控出气模式以使静压干气密封适应不同的运行膜厚和工况条件。图11 所示为出气模式可调静压干气密封的静环组件结构示意图。出气模式可调静压干气密封的静环组件主要包括静环及置于静环背腔内的调节环,静环端面上沿径向均匀开设有多列环形均压槽和节流孔,相邻列节流孔周向错排,且节流孔是连通密封端面均压槽和静环背腔的通道;调节环上与静环背部端面贴合的端面上沿径向均匀开设有集气槽,各集气槽的径向位置与节流孔一一对应,相邻列集气槽周向直排,每个集气槽通过开设于其内的通气孔与节流气腔连通,节流气腔通过静环侧面的供气孔与供气管路相通。当某一节流孔位于对应的集气槽范围内时,带压节流气方可通过通气孔、集气槽、节流孔而进入到均压槽和密封间隙内。在运行过程中,调节环可在外部机构的控制下旋转不同的周向角度,进而实现集气槽与节流孔的不同匹配,达到调控出气模式的目的。
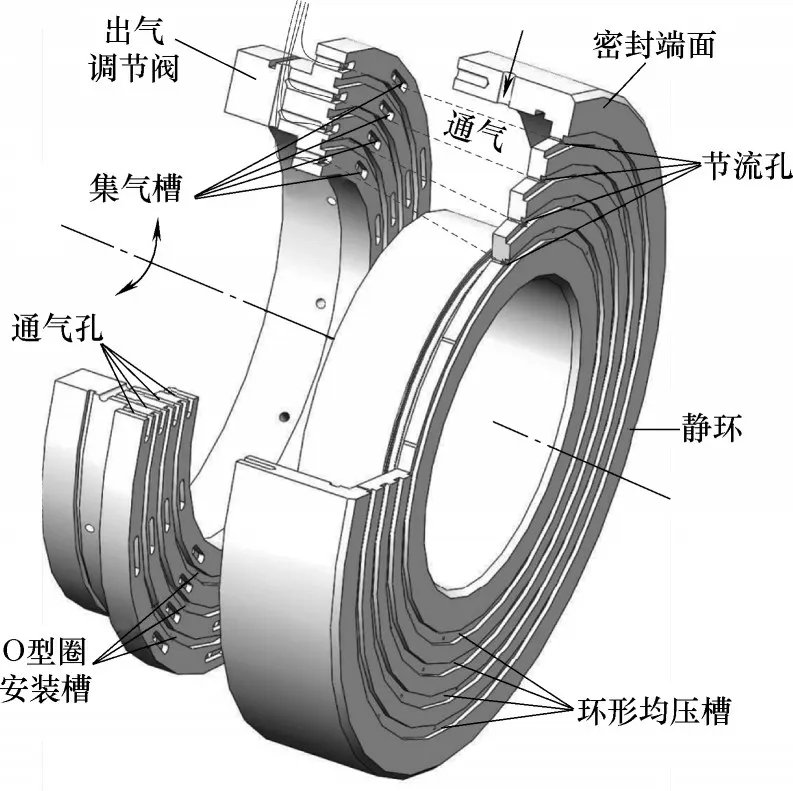
图11 一种出气模式可调静压干气密封静环及调节环结构示意图Fig.11 Geometric structure of stator ring and adjust ring of a hydrostatic dry gas seal with adjustable exhaust mode
以径向四列节流静压干气密封为例,图12示出了随着调节环周向夹角变化时所呈现的出气模式,图中阴影部分区域表示集气槽和对应的节流孔重合。在调节过程中,静环和设于其上的节流孔始终不发生周向转动,而调节环和设于其上集气槽发生周向偏转。从图中可看出,随着调节环的周向旋转,出气模式可调静压干气密封先后呈现出8 种出气模式,分别对应出气模式I=1000、1100、0100、0110、0010、0011、0001 和1001,其中模式1、3、5、7属于径向单列节流供气,模式2、4、6 和8 属于径向双列节流供气。

图12 不同调节环周向夹角对应的静压干气密封出气模式Fig.12 Exhaust modes of hydrostatic dry gas seal with different circumferential angle of adjust ring
图13 所示为八种出气模式对应的新型静压干气密封开启力、内泄漏率和耗气量。从图中可看出,不同出气模式下的静压干气密封表现出的开启力、内泄漏率和耗气量等稳态性能各异。为获得较大的密封开启力,建议取径向双列节流供气模式,其中模式4 具有最大的开启力;随着调节环周向角度增加,提供节流气的节流孔位置逐渐向内径侧移动,故而引起内泄漏率的不断增加,而耗气量基本只受节流孔列数的影响。若以最大密封开启力为目标,并兼顾低内泄漏率,建议选取出气模式4;若以最小内泄漏率为目标,并兼顾较大开启力,建议选取出气模式2;若以最小耗气量为目标,并兼顾较大密封开启力,则建议选取出气模式5。由此可见,相较于经典的单列节流静压干气密封,所提出的出气模式可调静压干气密封可通过调节出气模式以在较大密封开启力、低内泄漏率和低耗气量之间达到更好的平衡。

图13 不同出气模式对应的静压干气密封稳态性能参数Fig.13 Steady-state performance of hydrostatic dry gas seal with different exhaust modes
3 结 论
(1)径向多列节流静压DGS 的开启力和气膜刚度较单列节流供气静压DGS 显著提高,最大增幅分别为15%和25%,不过也会带来内泄漏率和耗气量的增加。靠近外径侧和内径侧的双列节流供气静压DGS(I=101)在膜厚较小时具有最佳的气膜刚度,而靠近外径侧和径向中间的双列节流供气静压DGS(I=110)在膜厚较大时能在获得较大开启力和气膜刚度的同时兼具较低的内泄漏率。
(2)提出一种出气模式可调的静压干气密封结构,通过静环背部调节环周向角度的控制可实现不同出气模式的转换,进而满足高气膜承载力、低内泄漏率和低耗气量的功能需求。
符 号 说 明
d——节流孔直径,mm
h——气膜厚度,μm
hd——均压槽深度,mm
I——节流孔供气组合
kz——气膜刚度,N·μm-1
l——节流孔长度,mm
N——节流孔个数
po,pi——分别为密封外径压力和密封内径压力,MPa
ps——节流气压力,MPa
qi,qo,q——分别为密封内泄漏率、外泄漏率、耗气量,m3·s-1
r——节流孔位置半径,mm
ri,ro——分别为密封端面内、外径,mm
w——均压槽宽度,mm
下角标
i——密封端面内径
o——密封端面外径
