基于神经网络的多卫星姿态协同控制预测模型*

宁 宇，宫经刚，曾海波

0 引 言

多卫星姿态协同控制，常用于编队飞行卫星任务场景[1].随着空间技术和应用的发展，在轨操作与服务已经开始转入实际应用阶段[2].操控航天器通常需要以非合作目标作为服务对象，在执行精细操作任务之前或过程中，若使用多个小卫星形成长基线多向辅助局部建模或实时监控，则能够大幅提升操作的精度和安全性.本文基于该背景，针对多卫星姿态协同控制进行智能控制方法研究.

在航天器编队协同控制中，通常使用多智能体系统一致性理论[3].MEI等[4]讨论了离散时间一阶积分器组成的多智能体系统对于虚拟领导者的一致性跟踪问题.SCUTARI等[5]研究了固定拓扑结构下基于相对状态的离散时间线性多智能体系统的一致性协议设计问题.WANG等[6]利用反馈线性化方法将一类非线性智能体网络化为线性标准型，设计了一致性协议，并分析了协议的性能指标.LUO等[7]讨论了二阶多智能体系统在通信时滞存在与否两种情形中，如何设计保证编队成员速度收敛于期望值的协同算法.近年来，基于神经网络的智能控制理论也在逐步应用于航天器控制[8].刘金琨[9]详细介绍了神经网络监督控制、直接逆控制、自校正控制、内模控制、预测控制、自适应控制等方法.曲汝鹏[10]基于神经网络自校正控制器实现卫星姿态控制，在干扰力矩变化情况下达到良好的控制效果.ZOU等[11]基于终端滑模和Chebyshev神经网络设计了航天器的有限时间姿态跟踪算法，可自主在鲁棒控制和智能控制算法之间切换.GAO等[12]将指数趋近律滑模控制与神经网络控制相结合，设计了实时调节指数趋近律参数的卫星编队飞行控制方法.

本文研究中，面向多卫星近距离对空间目标协同观测任务中的姿态指向协同控制问题，基于神经网络系统级状态预测，通过对卫星模型的预测控制方法和卫星整体输出状态预测，匹配有时延情况下的理想一致性控制协议，完成协同控制.与常规神经网络控制系统中，由神经网络取代控制器或优化控制参数不同，本文使用神经网络对系统级状态预测，从而对基于理想运动模型设计的控制参数进行修正计算，以适应复杂任务场景和多变空间环境.通过仿真验证了算法的有效性.

1 系统设计机理

在本文控制系统设计中，不需要对卫星运动进行建模，而是首先建立适用于某个控制方法的系统状态模型，以PID控制为例，建立标准的二阶运动模型，为该模型设计理想的参数，作为虚拟控制输出，将控制输出通过第一个神经网络环节后，直接生成适用于当前卫星姿态控制的实际控制输出.在多卫星协同控制中，各卫星互相传递姿态和位置信息，通过一致性控制理论保证各卫星间控制一致性.在某卫星一致性协议中使用其他卫星状态量时，无法保证所接收的信息是实时的，一般具有延时特性，此时使用第二神经网络，对其他卫星的运动状态进行预测，将预测值输出至一致性协议中，从而保证各卫星具有高度统一的控制目标和控制效果，而该卫星本体控制则使用第一神经网络，进行系统级预测，获得最终控制量输出.

第一神经网络选用多隐层神经网络模型[13]进行预测，神经网络计算公式如下所示:

z(l+1)=W(l)a(l)+b(l)

(1)

a(l+1)=f(z(l+1))

(2)

(3)

其中，a(l)表示第l层的激活值，z(l)表示第l层的加权和，W、b为系数.

第二神经网络需要基于前一步控制中的系统状态，选用循环神经网络模型[14]进行预测，计算公式如下所示：

st=f(Uxt+Wst-1+b)

(4)

ot=Vst

(5)

其中，st为t时刻加权和，ot为t时刻输出，U、W、V、b为系数.

所选用的一致性协议[15]如下所示：

k3(qi-qd)

(6)

其中，下标i、j表示第i、j个卫星的相应参数，下标d表示理想值，ui是控制量，pi、pj是姿态角，qi、qj是角速度，N为航天器数量，τ为时延，k1、k2、aij为系数.

各卫星均使用该一致性系统控制协议，通过对其他卫星运动的相互预测，以及对自身控制能力的预测，进行姿态协同控制，保证在动态情况下迅速达成一致性并保持稳定.

2 智能控制模型

在多卫星协同执行任务中，由于任务场景环境复杂，同时各卫星之间信息传输延迟问题，会导致一致性控制效果不理想.本文在多卫星协同控制中，基于智能控制理论，采用人工神经网络方法，建立卫星智能控制模型，解决上述问题，保证协同控制精度.

2.1 控制与输出预测

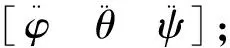
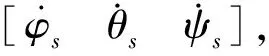
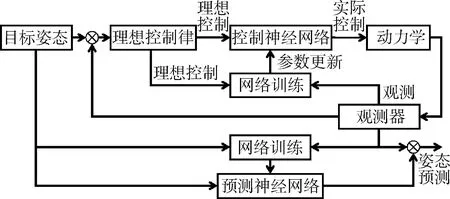
图1 单航天器神经网络自学习控制与输出预测

2.2 一致性协同控制

在多航天器协同控制过程中，本航天器对其他航天器当前时刻的姿态运动情况进行预测后，将预测值纳入至一致性协同控制协议中使用.控制模型如图2～3所示，是基于两类预测方式下的协同控制模型.图中，方框内编号为1或1-1等表示卫星1模型；编号为2或2-1等表示卫星2模型.模型一采用对其他航天器姿态和角速度的预测方式为，对输入目标和实际控制情况的映射关系进行神经网络学习和预测；模型二在本航天器中存储了其他航天器的控制模型和参数，通过对输入控制量和实际控制情况的映射关系进行神经网络学习和预测.对于卫星1，一致性控制量表示方式如下所示.

u1=fANN1(fCON(AttR1,fRNN2(AttS2)))

(7)

其中，u1为控制量，fANN1表示第一神经网络，fRNN2表示第二神经网络，fCON表示一致性控制协议，AttR1表示卫星1实际姿态，AttS2表示卫星2目标姿态.实际控制量是对理想的一致性协议理想控制量的跟踪，同时二者共同用于训练跟踪模型.

两种模型都能够达到理想的协同控制效果.模型一在实现上更为简明、稳定性好；模型二对实际系统还原性更强，但建模复杂.在模型二的基础上，还可以进一步对其他航天器进行详细的建模，完全和其他航天器的控制系统架构保持一致，并对不可知部分进行神经网络预测.图中，实线框代表卫星1，虚线框代表卫星2.

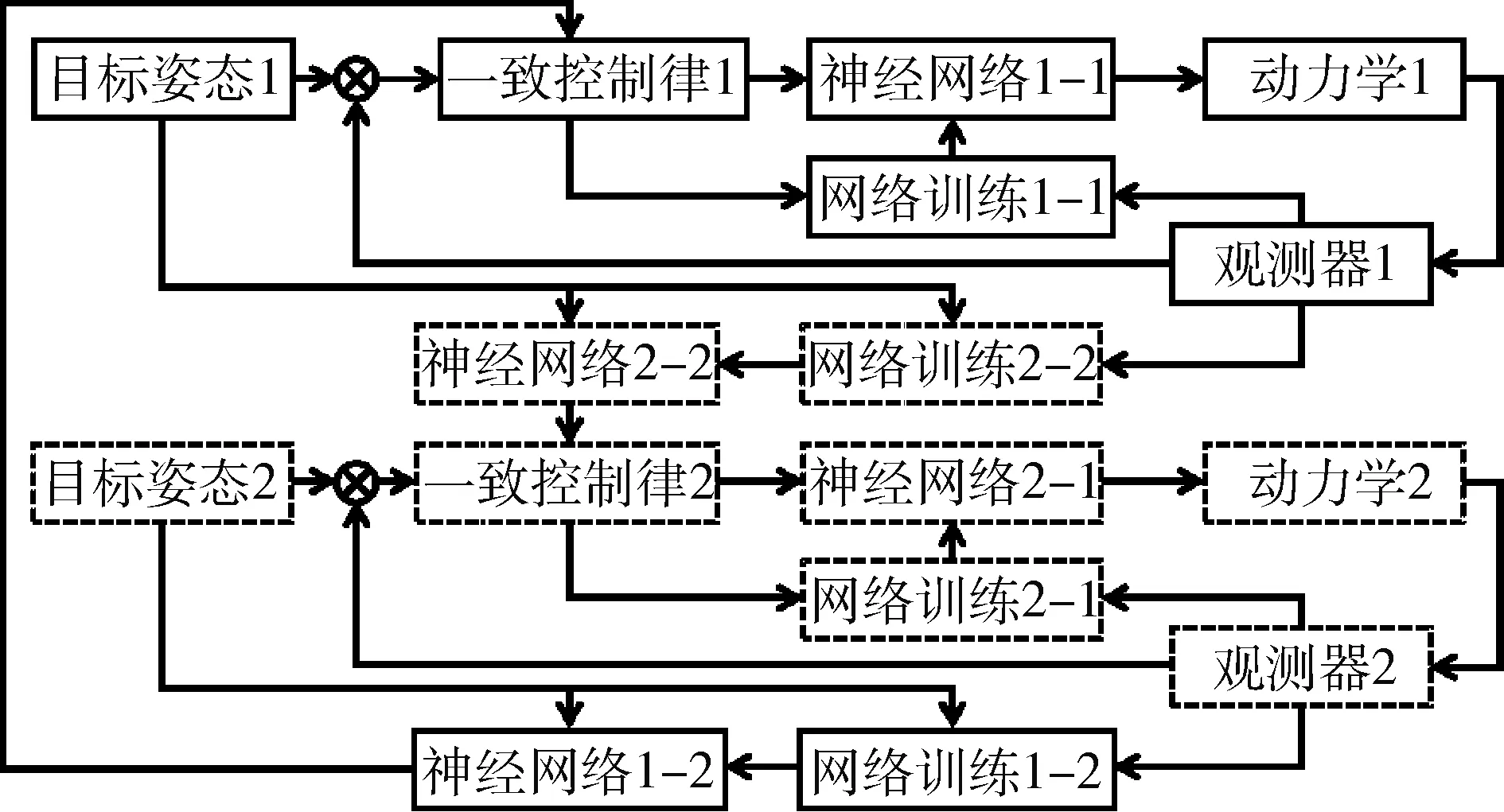
图2 多卫星智能协同控制模型一

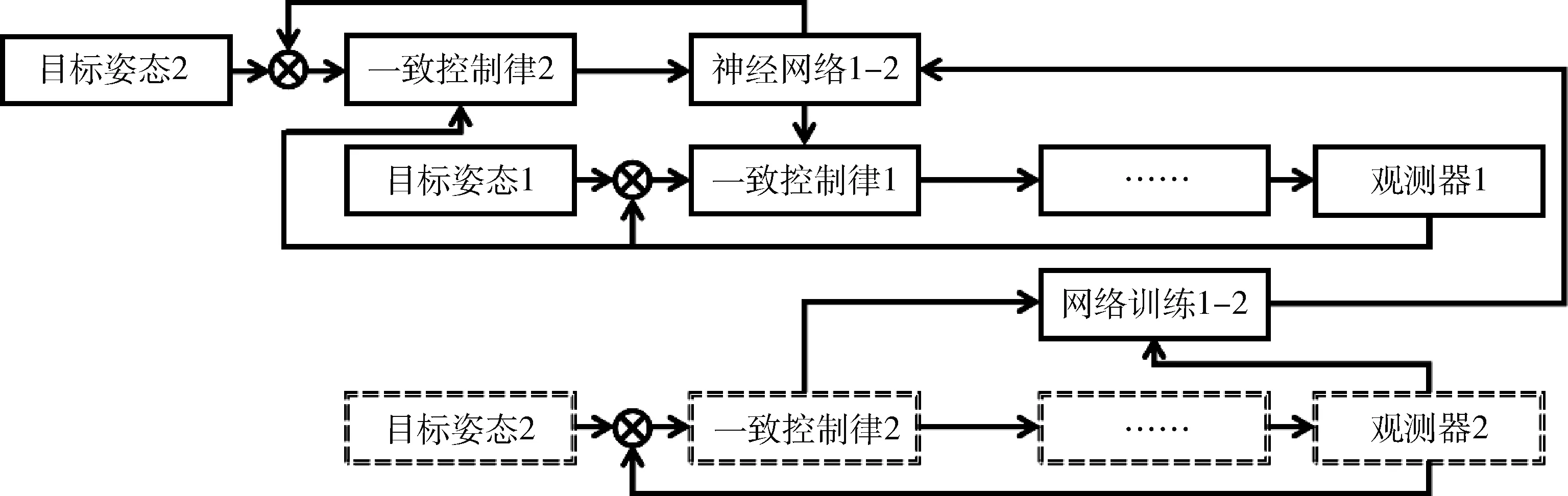
图3 多卫星智能协同控制模型二

2.3 预测量使用方式

各卫星对协同姿态控制都进行实时解算，但各卫星只能保证实时获取自身的观测量，而其他卫星的观测量具有一定延迟性，需要使用神经网络预测量.对于预测模型的训练和使用，分为两级运算，第一级为实时预测与控制，使用当前预测模型预测信息和本卫星测量信息；第二级在当前时刻获取之前时刻的其他卫星测量信息之后，对预测模型进行训练，完成参数更新后，超实时预测姿态信息，将本级数据在时间上达到与第一级数据同步，然后取代第一级数据，从而保证所使用的数据为最新精确数据.时序示意图如图4所示.

3 数值仿真结果

各卫星运动模型选用刚性本体并带有挠性转动部件的模型[16]；观测器输出卫星姿态和角速度；使用等效姿态角评价控制情况，等效姿态角指某卫星指向在目标上的投影点，反向解算至另一卫星指向的角度；控制模型中对卫星转动惯量装订参数，相比于实际卫星放大1/3，并由仿真结果可知，智能控制系统不受影响.

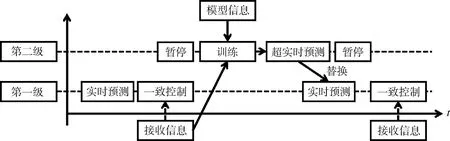
图4 预测模型训练和使用时序示意图

3.1 预测控制方法

使用神经网络智能控制方法对单卫星进行姿态机动控制.选用场景为对目标近距离详察卫星视线方向，在目标卫星本体落点，沿直线轨迹运动情况.无观测误差理想控制情况下，姿态角在经过神经网络初期训练收敛后，能够有效跟踪理想控制情况；在神经网络训练中加入观测误差情况下的控制情况如图5～6所示，其中训练数据卫星姿态角加速度利用陀螺观测角速度差分获得，陀螺角速度随机误差为3×10-7rad/s，姿态角和姿态角速度能够快速收敛，具有微小误差.

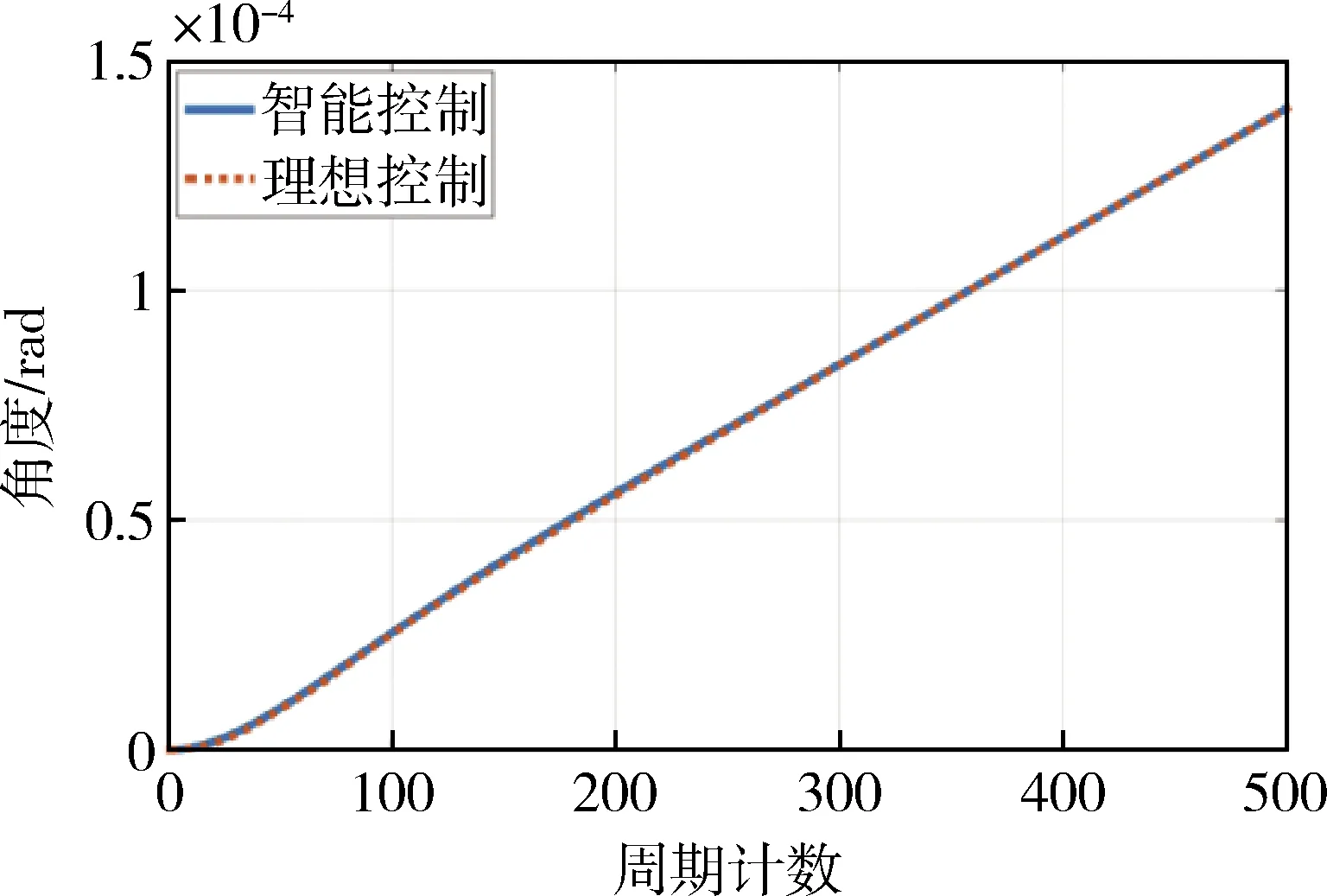
图5 姿态控制跟踪曲线

3.2 输出状态预测

对卫星的输出状态预测情况，在无测量误差情况下，神经网络预测误差在1urad附近震荡，当有针对性的进行模型架构调整后，能够持续提高精度，对此本文不做详细讨论；当对观测量加入10urad(1σ)随机观测噪声后，如图7～8所示，预测值的噪声特性和所加入的观测噪声特性一致.因此，输出状态预测是有效的.

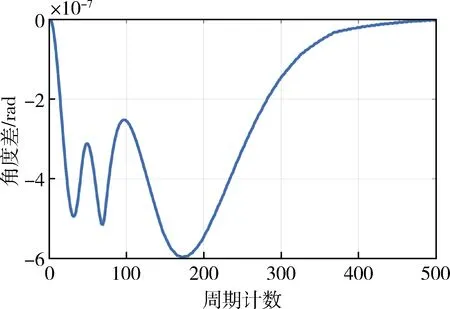
图6 姿态控制误差曲线

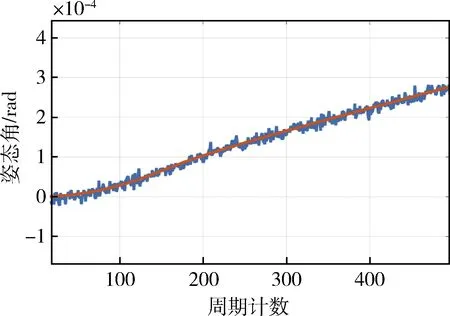
图7 姿态预测曲线

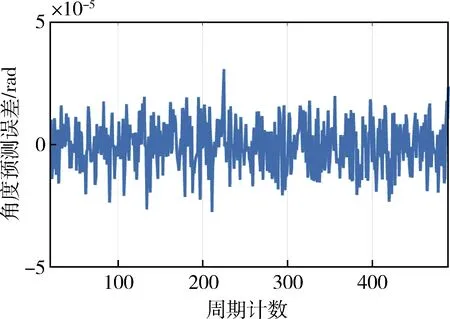
图8 姿态预测误差曲线

3.3 协同控制

通过神经网络对其他卫星姿态控制情况进行预测，带入本航天器的协同控制协议中使用，输出协同控制量的控制情况如图9至图14中所示.其中，假设监测卫星距空间目标200 m；两个监测卫星与空间目标连线夹角约90°；监测卫星视场指向在空间目标表面交点移动长度为20 m，移动速度为0.01(°)/s.

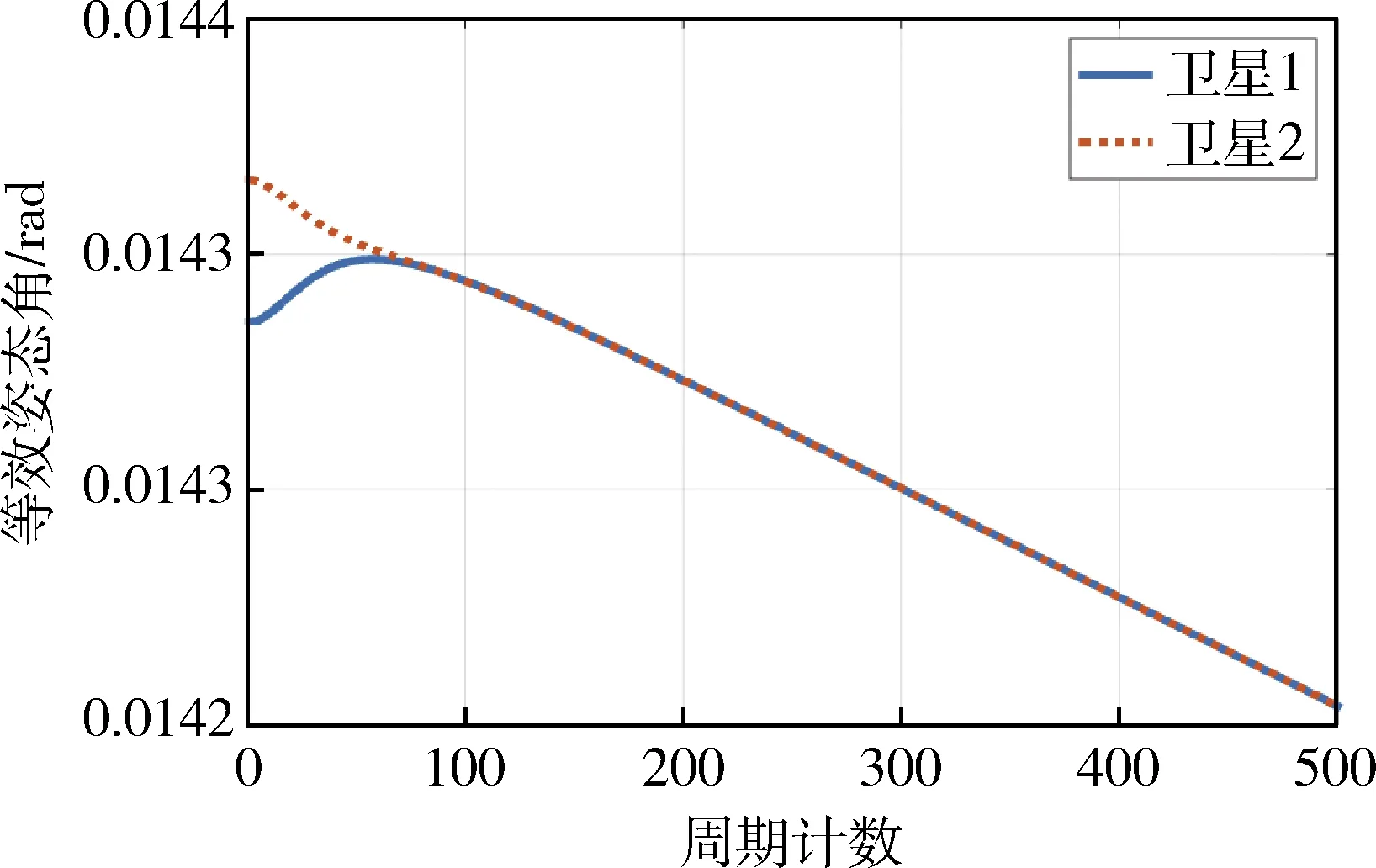
图9 姿态协同控制曲线一

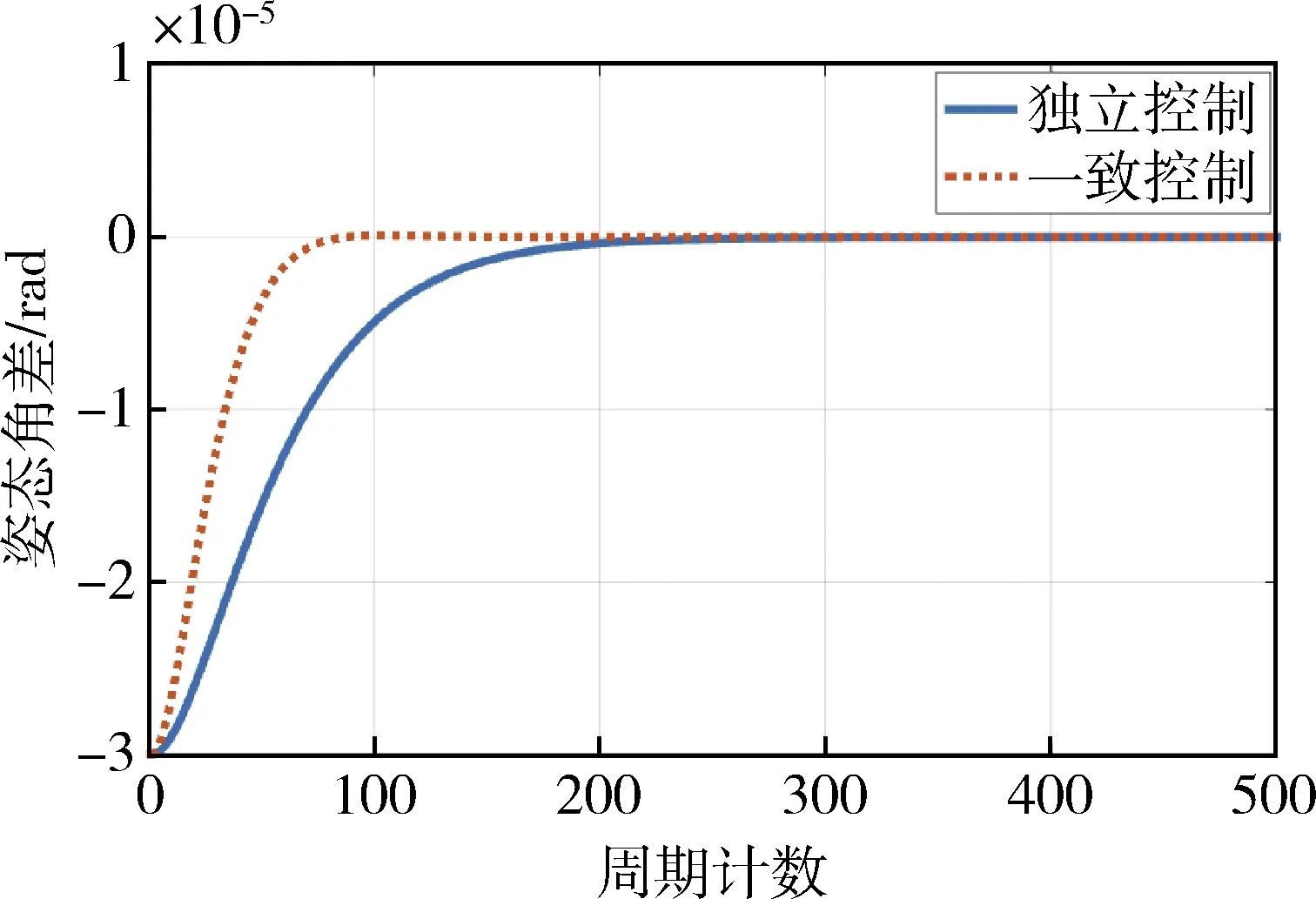
图10 姿态协同控制比较曲线一

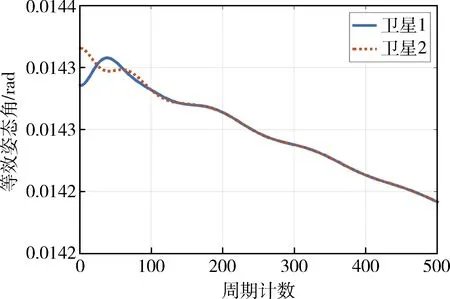
图11 姿态协同控制曲线二

(1)无观测误差控制情况

图9表示协同控制轨迹，图10表示协同控制和独立控制比较.由图10可知，通过协同控制能够使多航天器之间姿态控制情况快速统一，协同控制使协同时间相比于独立控制缩短了约50%.

图11～12是将独立控制系统调整为较差控制参数情况下的控制曲线，以便于更有效地展示协同控制效果.无协同控制时，系统长期大幅震荡；在协同控制下，控制误差迅速收敛.

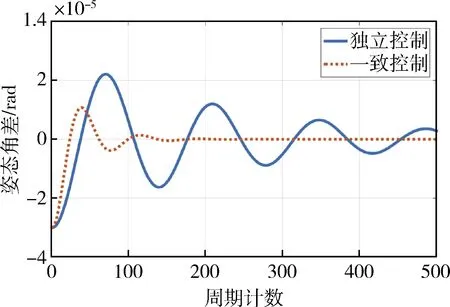
图12 姿态协同控制比较曲线二

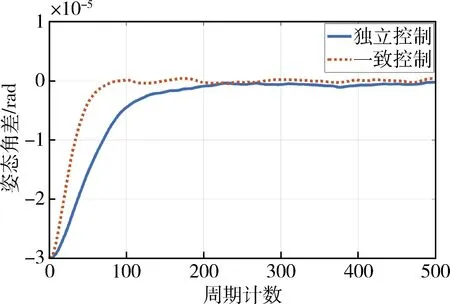
图13 姿态协同控制比较曲线三

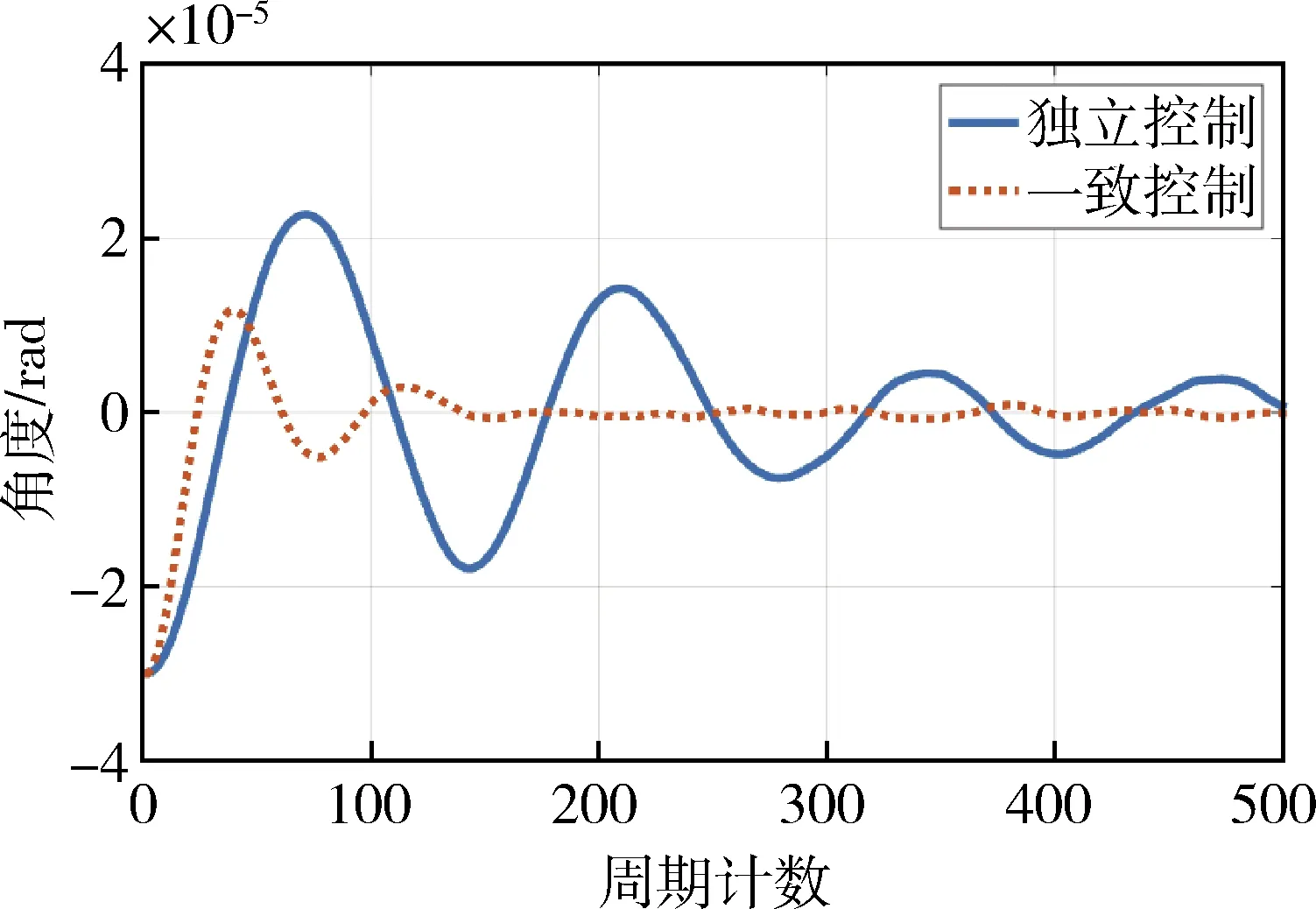
图14 姿态协同控制比较曲线四

(2)有观测误差控制情况

加入观测误差后，协同控制系统的控制情况如图13～14所示，控制情况基本与前文无观测误差一致，只是增加了受观测噪声影响的控制误差.其中，姿态测量随机噪声10urad(1σ)、陀螺角速度随机噪声3×10-7rad/s情况下.

4 结 论

针对空间操控任务中多卫星近距离协同对目标监测任务的复杂执行环境，研究了基于神经网络系统的智能姿态协同控制.采用循环神经网络对其他卫星姿态控制情况进行预测，引入至理想模型下的一致性控制协议后，采用另一神经网络将理想控制量转变为实际系统控制量，完成协同控制.本方法对各类型干扰及模型误差有良好的适应性.仿真结果验证了方法的有效性.