空间光学敏感器成像组件抗力学稳定性分析与评价*

张慧锋，孙 艳，李春江，孙建波，周建涛，曹明宇

0 引 言

空间光学敏感器是指用于航天器控制与导航系统，通过对天文目标或者人工目标的几何或者光度信息的光电感知和处理，或者对光子飞行时间探测和处理，获取并确定航天器姿态和导航信息的一类空间光电仪器.成像类空间光学敏感器所追求的目标是通过成像或者扫描等手段，获取并确定目标稳定性特征的位置和状态[1-2].成像类空间光学敏感器包含星敏感器，交会对接光学成像敏感器，导航/避障相机等.成像类光学敏感器的核心组件是成像组件.成像组件通常包括光学系统，成像探测器芯片，基准镜以及相关安装结构等部分.由于航天器从制造到任务终止全寿命周期内需要经受振动、冲击、加速度等力学环境[3]，成像组件各部分间的抗力学性能成为保证整机精度的基础.

成像组件的各部分通过装配连接在一起，装配方法有螺钉连接、胶接等.其中，机械紧固件连接在敏感器结构设计中应用最广泛.机械紧固件连接的优点有，容易拆卸、强度分散性小等，缺点有连接可能漂移、引入应力集中并导致脆性材料破坏等[4].敏感器在紧固件装配完成后经历力学环境，如果结构或装配方式不合理，结构之间会发生微小滑移现象，导致连接漂移，造成测量坐标系相对于机械安装坐标系之间的偏差.该误差属于基准稳定性误差[5].因此，需要对成像组件开展抗力学分析与设计，保证组件的抗力学稳定性.

近年来，由于我国航天器对地观测精度以及深空探测导航精度需求不断提高，对航天器抗力学环境分析与设计、航天器部件热稳定性的研究工作较多.文献[6-7]分别应用叶簧结构和Bipod结构对遮光罩支撑结构进行优化设计，并进行了敏感器抗力学环境分析与设计；文献[8-11]都对航天器部件结构开展了抗力学环境分析与设计，以满足结构的抗力学性能要求.以上文献主要通过力学分析得出结构基频满足刚度要求，在力学环境下的应力分布满足材料强度要求，但并未对结构间的相对滑移开展研究.结构基频作为抗力学稳定性的性能指标，虽然具有通用性，但没有直接反映各组件之间的滑移量，所以对于滑移量导致的各部件间的角度变化也无法计算.由于空间光学敏感器测量精度要求越来越高，其抗力学稳定性与航天器其他部件相比要求更高，对于位置测量的光学敏感器和光学相机，对滑移量的要求更严格，对探测器在力学试验前后位置的变化提出了具体要求.本文将从成像组件结构形式出发，进行力学分析和试验，以解决光学敏感器成像组件研制过程中普遍存在的结构滑移问题为主要目标，开展抗力学稳定性分析与定量评价，为产品研制提供数据支持.

1 成像组件结构

光学敏感器成像组件结构由主体结构，光学系统，成像芯片，光学系统安装台，调焦环等结构组成，如图1所示.光学系统、调焦环与光学系统安装台通过轴孔配合+螺钉紧固的方式固定；光学系统安装台与主体结构通过螺钉紧固的方式固定.成像芯片用硅橡胶粘接在主体结构上.

为了实现敏感器整机姿态测量精度，光学系统需要和成像芯片光敏面实现多自由度对准.光学系统和成像芯片不仅要满足对准精度要求，也需要具备相当的抗力学稳定性，即保证在力学环境后，对准精度不发生变化(或变化足够小)，不影响敏感器测量精度.

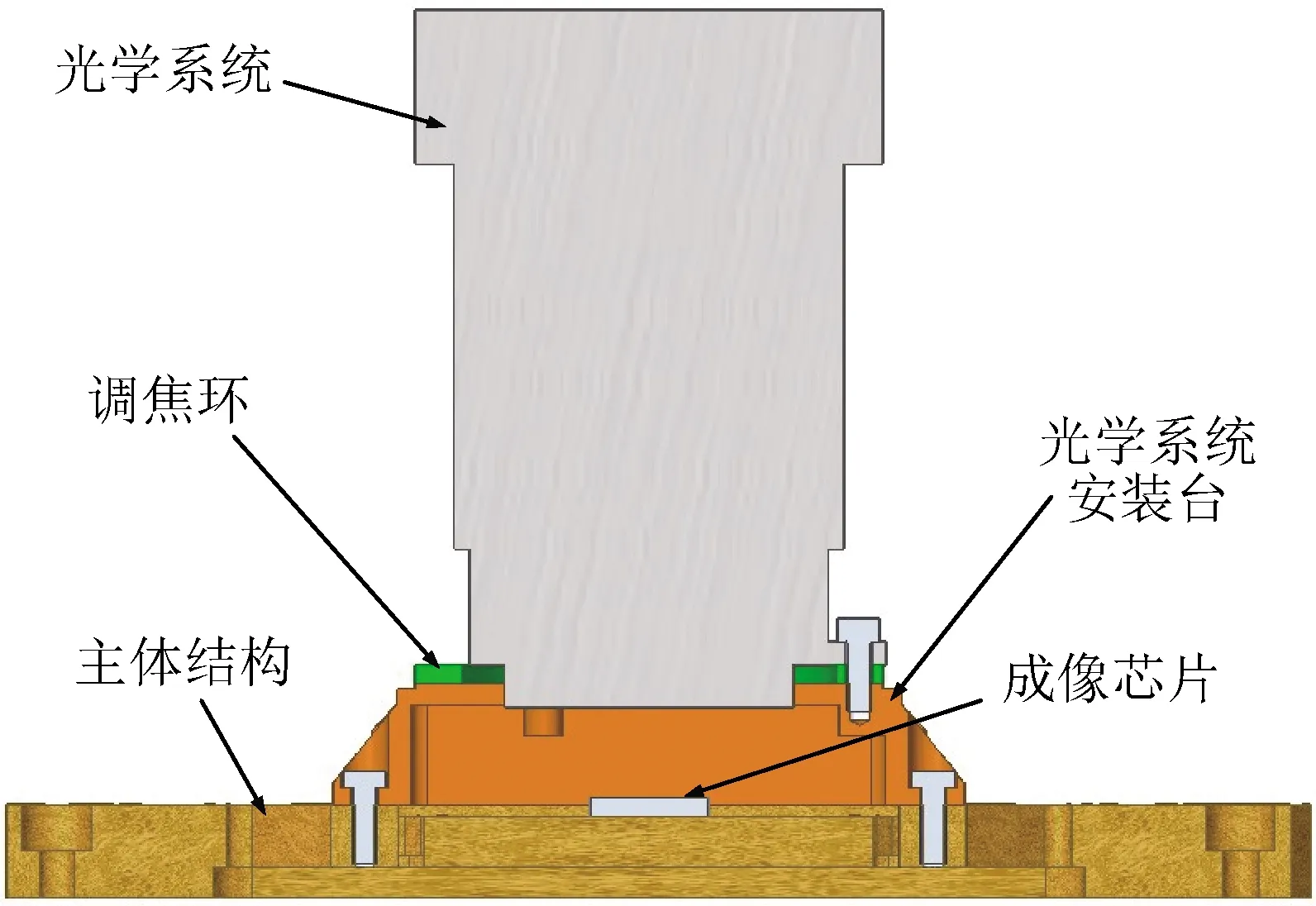
图1 成像组件结构示意图

2 抗力学稳定性仿真分析与验证

抗力学稳定性是抗力学性能的一部分.空间光学敏感器的抗力学性能通常用刚度和动强度来衡量，在结构设计过程中，刚度和强度主要通过仿真分析来计算.其中刚度的主要指标为一阶基频；动强度是指在随机、冲击等力学环境条件后，产品仍可正常工作，功能、性能不发生变化，产品各零件、组件和元器件无破坏等异常情况.本文首先进行刚度和强度仿真分析，对抗力学稳定性进行初步评价.

2.1 有限元模型

对第1节介绍的成像组件进行有限元建模，应用有限元软件ANSYS 18.0 Workbench对装配关系建模.其中，对光学系统安装台与主体结构的紧固螺钉进行详细建模，并添加预紧力；根据实际工作情况，对各接触面建立装配关系，并添加摩擦系数.

模型建立后，对模型划分网格，如图2所示.其中对接触面的网格划分更细，对需添加预紧力的圆柱面，沿螺钉轴线方向划分至少两层网格，如图3所示.

图2 有限元模型

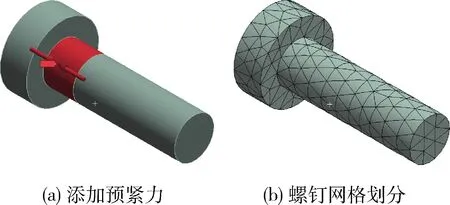
图3 螺钉有限元模型

2.2 力学分析及试验条件

设计敏感器产品力学试验条件，如表1、表2所示.

随机试验前后进行扫频实验，扫频范围：10～2 000 Hz，量级0.5g，速度2 oct/min.

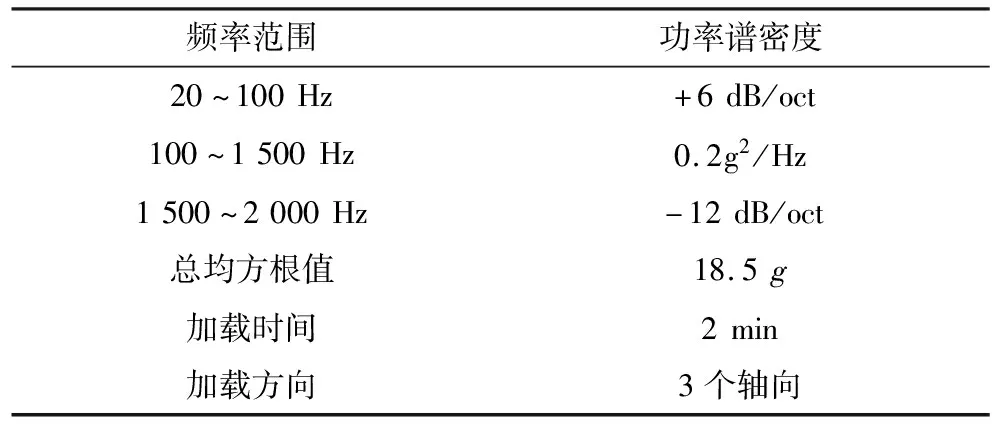
表1 随机振动分析及试验条件

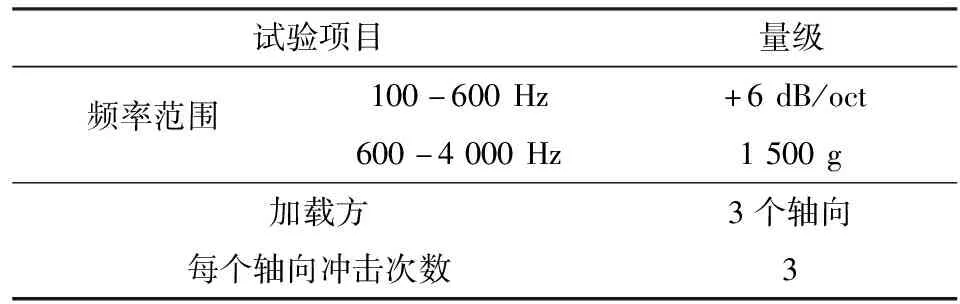
表2 冲击响应谱分析及试验条件

首先进行静力学分析，应用ANSYS Workbench中Static Structure模块，载荷为螺钉预紧力，并在主体法兰的4个安装孔处添加固定约束.分析求解得到螺钉预紧力条件下的应力状态.在此应力状态下，进行模态分析，应用Modal模块.在模态分析的基础上，进行随机振动分析和冲击响应谱分析，应用Random Vibration模块和Response Spectrum模块.2.3 计算及试验结果

经模态分析和扫频试验，前六阶基频及试验结果如表3所示.可以看出，分析结果与试验基频误差较小，验证了本文所用分析方法的有效性.组件的前三阶振型如图4所示，其中前两阶为绕X向和Y向的摆动(光轴方向为Z向)，第三阶振型为沿Z轴的上下振动.

当主体结构随机量级为18.5g时，3个测点的响应值如表9所示.其中，测点1在图5所示光学系统上端面基准镜附近，测点2位于D点，测点3位于D′.可以看出，结构出现不同的程度的放大效应.在随机振动和冲击振动下，可以分析得到结构的应力分布，最大应力不超过材料许用应力，且留有安全余量，本文不再详述.

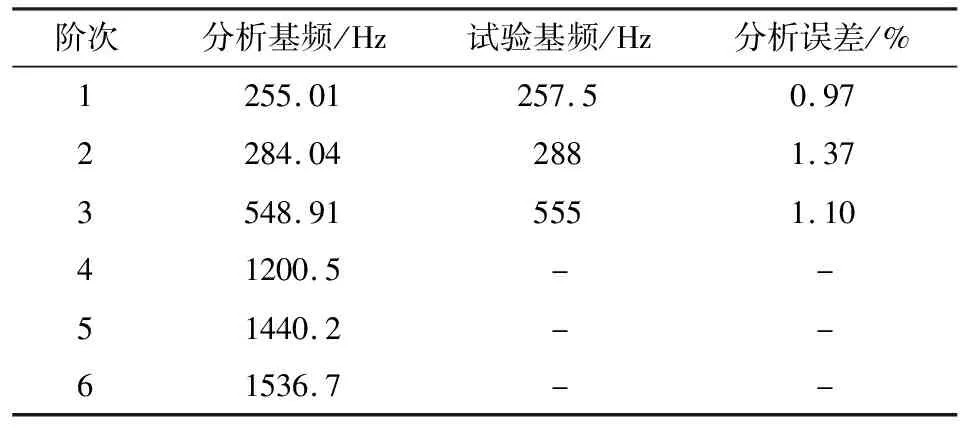
表3 计算及试验基频

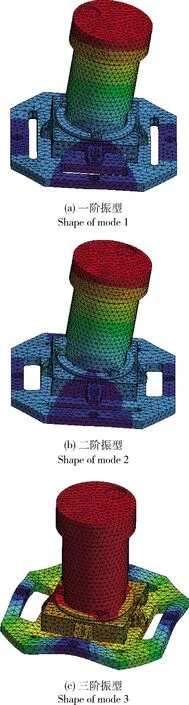
图4 振型

由于结构滑移的发生在结构仿真过程中无法直接模拟，本节的仿真分析主要目的是提供一种改进的建模方法，可以更准确地计算组件的基频，进而得到更准确的测点响应值；基频和测点响应值反映了结构刚度，刚度越大，则组件的抗力学稳定性越好，结构的相对滑移也越小.

综上可知，现有的仿真分析方法只能定性反映结构的抗力学稳定性，因此，本文将在后文提出一种实验方法来定量测量结构的相对滑移.

3 抗力学稳定性定量评价方法

航天器结构除刚度、强度等性能要求以外，还有抗力学稳定性要求.对于成像组件，需要保证在经历力学环境后，测量坐标系、机械坐标系和光学系统坐标系之间的转换矩阵不发生变化，即各结构之间抗力学稳定性.因此，本文提出用两个指标来评价成像组件的力学稳定性，并通过实验方法来对这两个指标进行测量：

1)连接面相对滑移量；

2)光学系统机械基准相对于主体结构的角度变化量.

其中第1项指标通过测量结构的相对位置来实现，如图5所示，通过测量光学系统安装台和主体法兰上的对应点(如A与A′)的高度差，并对比力学试验前后的测试值，实验前后的差值代表滑移量.所用测试设备为测高仪(一维位移测试仪)，分辨率为0.1 μm，重复精度为0.5 μm.

第2项指标通过在主体法兰、光学系统、光学系统安装台上安装基准镜，测量基准镜之间的角度差并记录，对比力学试验前后的测试值，实验前后的差值代表光学系统机械基准变化量.其中，基准镜用硅橡胶粘接于结构上，力学试验前后基准镜相对于结构的变化量较小，可忽略.所用测试设备为经纬仪，分辨率为1″，测量精度为2″.

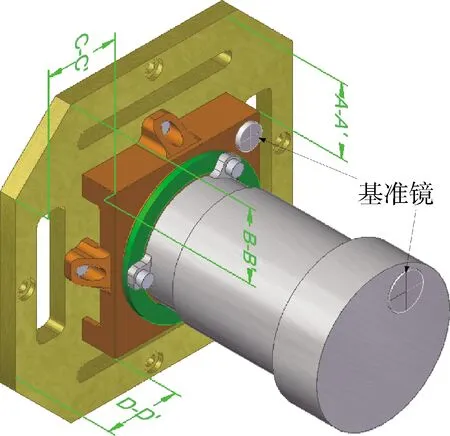
图5 滑移测试

图6 滑移测试实物图

4 评价方法应用实例

本文将3种结构形式的成像组件实验件进行对比，一种是图1所示结构(在下文中记为结构1)，另外两种是图7所示结构形式，即在光学系统安装台与主体结构之间增加圆锥销(在下文中记为结构2)或圆柱销(在下文中记为结构3).应用第2节、第3节介绍的仿真分析方法和评价方法，对3种结构形式进行力学分析、力学试验.给出两种结构的仿真分析和力学试验结果；应用第3节提出的稳定性评价方法开展测试，给出测试结果.

图7 结构2与结构3

4.1 评价指标测试结果

结构1滑移测试结果如表4所示.其中，光学系统安装台在力学试验后，相对于主体结构发生的明显滑移，其中最大值超过0.05 mm；光学系统机械基准变化测试结果如表7第一列所示，其中光学系统机械基准变化超过11′.如果滑移和光学系统机械基准变化发生在产品试验阶段，则需要重新标定整机，造成时间和人力成本浪费；如果发生在发射阶段，将会造成较大系统误差，影响姿态敏感器测量精度.

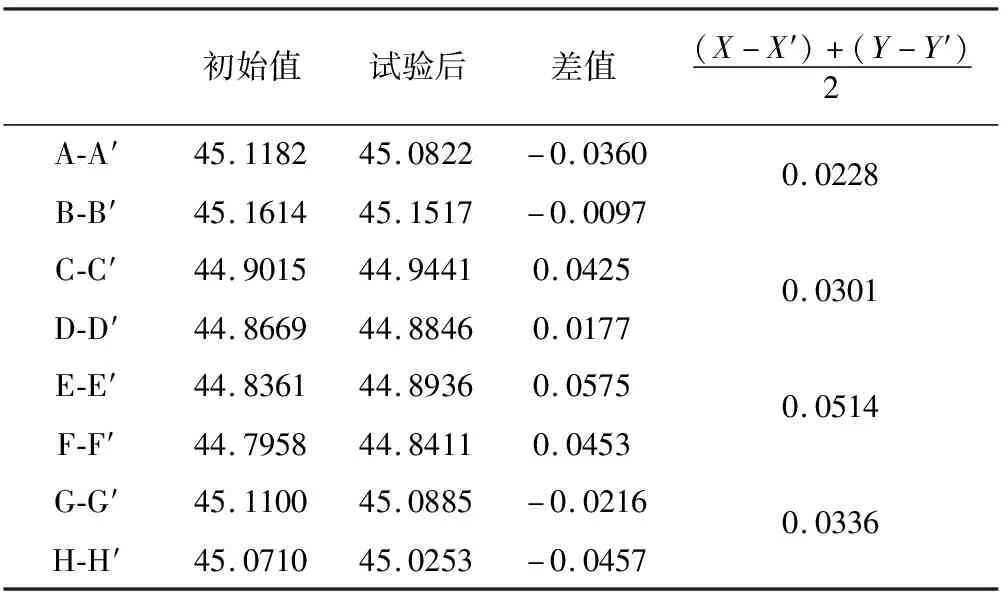
表4 结构1滑移测试结果

结构2和结构3滑移数据和光学系统机械基准变化数据如表5，表6和表7所示.结构1的最大滑移量0.0514 mm，而结构2的最大滑移量为0.026 mm，结构3的最大滑量则降低为0.006 mm；主体结构与光学系统机械基准偏差从原结构的675″降低为19.0″和8.0″.其中，光学系统与光学系统安装台角度相对变化较大，原因是机械基准与安装面平行度有误差，且两个接触的安装面非理想平面，当光学系统与光学系统安装台的基准镜安装距离较远，且光学系统安装孔间的距离较小时，如果有滑移则会放大角度误差.测试数据表明，在光学系统安装台与主体结构之间装配圆柱销和圆锥销后，结构稳定性得到大幅改善，其中圆柱销结构的改进效果更好.圆柱销结构优于圆锥销主要原因是，圆锥销在力学振动过程中圆锥销会相对圆销孔有少量滑出，造成定位精度下降.

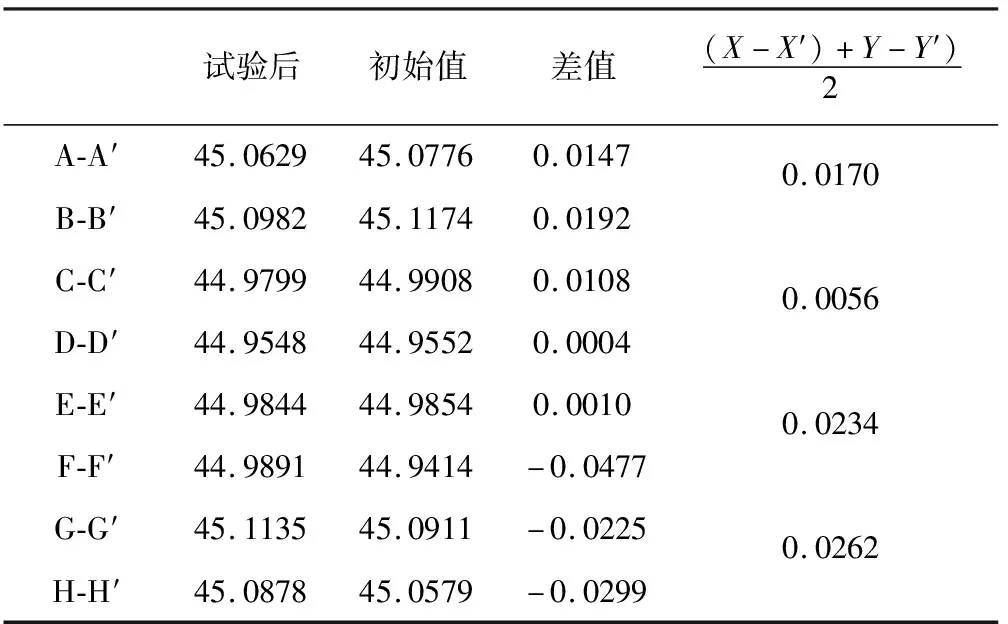
表5 结构2滑移测试结果

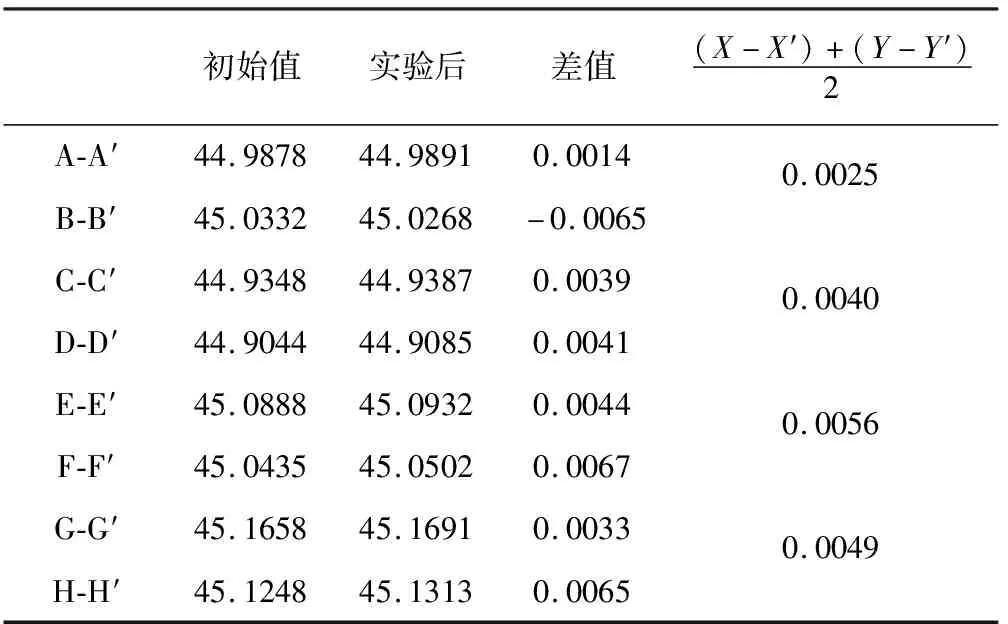
表6 结构3滑移测试结果

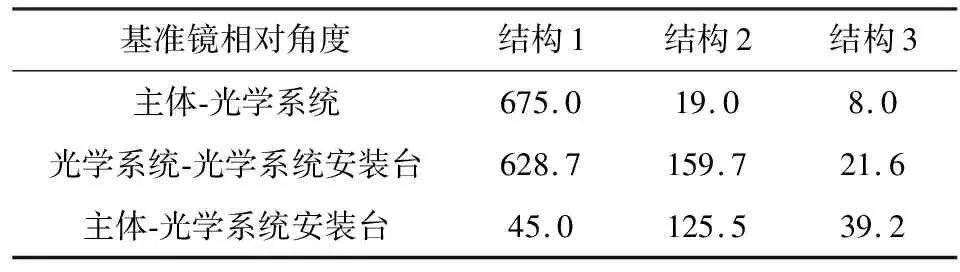
表7 光学系统机械基准变化测试结果

4.2 力学分析和试验结果对比

首先，对3种结构的刚度和量级放大作用进行数据统计和分析.其中结构基频如表3所示，结构1的一阶基频大于250 Hz，可满足敏感器刚度要求；测点放大结果如表9第一列所示，其中光学系统上端面量级出现了多倍放大，需要采取措施进行控制.

3种结构形式的基频数据和测点量级数据如表8和表9所示.其中结构2的一阶基频265.9 Hz，刚度优于原结构257.5 Hz，结构3的一阶基频则提高到272.2 Hz；光学系统上端面的测点量级从结构1的94.98g分别降低为80.33g和72.62g.数据显示，在光学系统安装台与主体结构之间装配圆柱销和圆锥销后，结构刚度都得到提升，测点响应降低.

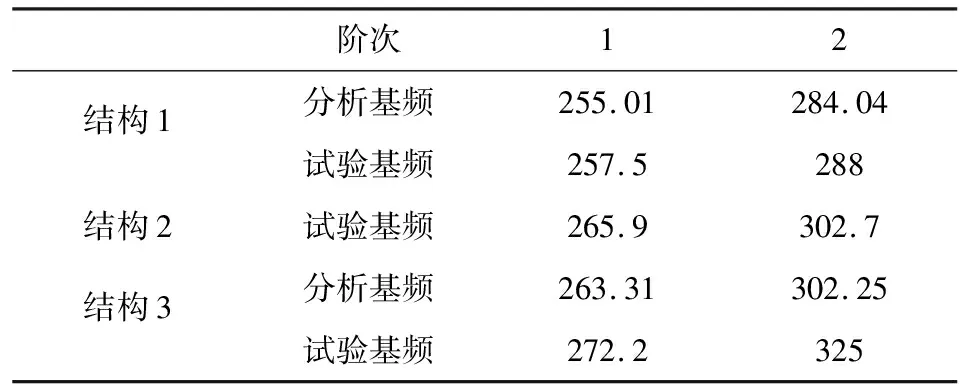
表8 3种结构的基频

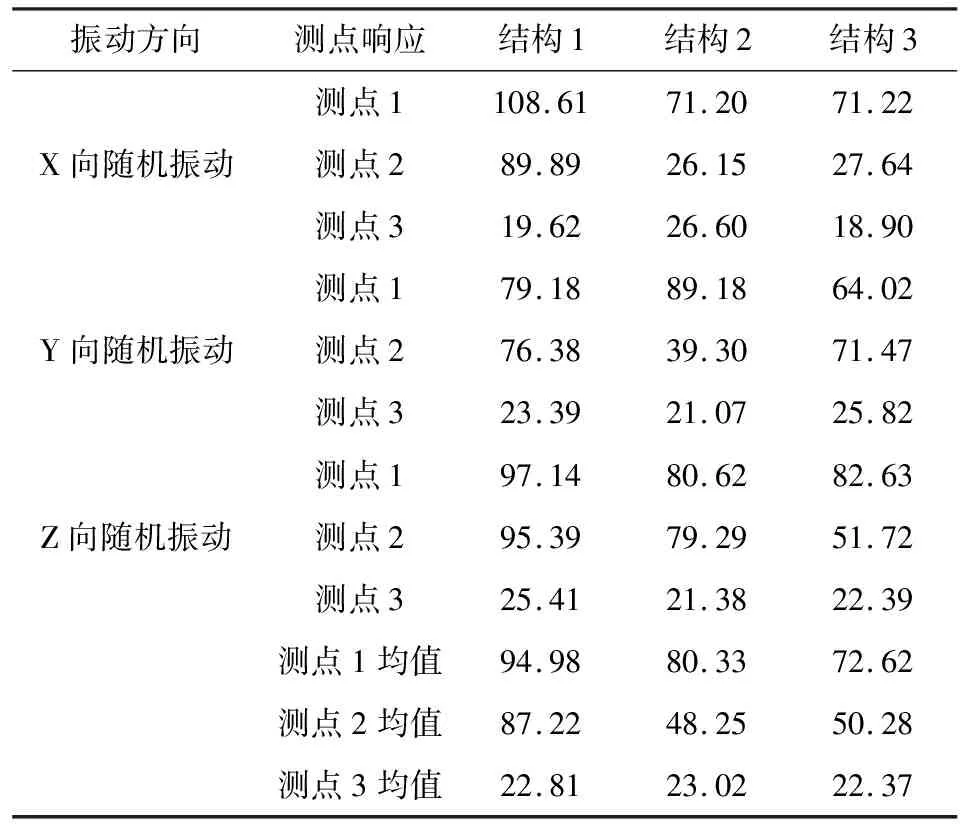
表9 随机振动测点响应值

4.3 评价效果

对比4.1节的评价指标测试结果和4.2节的力学仿真试验结果，可以看出，评价指标的对比结果与力学仿真和试验对3种结构的评价结论是一致的.但是本文提出的量化评价方法可以给出结构力学试验后的滑移值和机械基准变化值，为产品的研制提供数据参考.

5 结 论

本文首先对一种空间光学敏感器成像组件的结构进行了力学分析，其中对装配关系进行了详细建模，得到了成像组件的基频，并通过试验验证了分析方法的有效性.

由于仿真分析只能对抗力学稳定性进行定性评价，本文提出了实验方法来定量评价，详述了成像组件结构稳定性的评价指标，并给出了测试方法.

在提出评价指标后，对3种结构进行了力学分析和试验，测试了试验前后的滑移量和光学系统机械基准变化量.分析和试验结果表明，评价指标的对比结果与力学仿真和试验对3种结构的评价结论是一致的，而量化评价方法可以给出结构力学试验后的滑移值和基准变化值.

本文提出的力学分析方法、抗力学稳定性评价方法及测试方法，可推广应用于有抗力学稳定性要求的光学仪器中，尤其是对位置和角度对准精度变化敏感的空间光学仪器的研制过程.