对于动态目标的航天器鲁棒PD+快速跟踪控制方法*

王登峰，姚舒越，焦仲科，姚 鑫，李 由

0 引 言

在航天科技飞速进步发展以及科技工作者的一系列实践过程中，人类对于卫星的姿态跟踪控制问题给予广泛的关注和研究.其中，应用PD控制方法解决上述问题已发展为业界较为成熟且一般化的手段.PD控制律最早是由WIE等[1-2]在解决航天器的姿态跟踪控制问题时提出的.同时，WIE总结了一些相关的Lyapunov函数并且总结了普适的稳定性证明方法.而在最近，针对卫星姿态控制问题，JAMES[3]提出一种对PD控制方法改进的方法——无源PD控制律.本文内的方向余弦矩阵将被视作比例项引入控制律中.

PD控制方法之所以能够长期得到广泛的关注和应用，是因为其结构不复杂、物理含义明确、鲁棒性强等优势.但在某些方面也有局限，如：1)初始控制力矩过大，伴随着状态的减小，控制力矩会急剧下降，对控制律的利用效率较低；2)收敛速率较缓，姿态角速度的快速下降造成四元数的收敛速率减缓；3)无法完全利用已知参数，只能确定系统部分转动惯量参数.

针对控制力矩受限问题，JOVAN等[4]设计了一种鲁棒姿态跟踪控制律.针对PD控制器的收敛速率问题，VERBIN等[5-7]应用Back-stepping方法设计的角速度曲线具备快速收敛特性，设计的控制律实现了实际状态对设计参考轨迹进行跟踪.在文献[5]和[6]中则讨论了卫星的控制力矩限制问题，而文献[5]和[7]中讨论了卫星的角速度限制问题.但文献[5-7]中均缺少了对系统转动惯量不确定性的讨论.CAO等[8]考虑了转动惯量具有不确定性并加入外部干扰力矩，设计出了时间较优的控制律，并对卫星的时间最优角加速度与角速度进行了规划.针对卫星角速度受限问题，HU等[9-10]基于滑模控制和退步法为柔性卫星设计了姿态控制律.PD控制器不仅广泛应用于航天领域，而且应用于其他领域，例如LI等[11]基于遗传算法对PD控制器的参数进行了优化，文献中反映出控制器各项对于系统性能的不同影响，并提出针对收敛时间与稳态精度的参数优化方案.TATSUYA[12]与ZHANG[13]针对直升机的姿态控制设计了模糊PD控制器，由于直升机飞行时受到的干扰远多于卫星，作者对经典PD控制器加以改进，增强了其抗干扰性.SU等[14]针对四旋翼飞行器的姿态控制设计了非线性PD控制器，其系统状态经过非线性变换之后才输入到控制器当中，增强了系统的稳定性.

本文基于卫星控制力拒和角速度受限的情况，改进了传统PD控制律，在不改变稳定性证明方法的前提下设计了PD+控制器，设计出一种时间较优的滑模面，实现系统状态沿设计的滑模面运动.对控制力矩饱和给出解决方案，对姿态角速度与控制参数之间的关系进行讨论.最后通过仿真验证算法的有效性.

1 动力学与运动学模型

姿态跟踪控制问题中误差角速度的动力学模型为[15-17]

(ωe+Rωd)×J(ωe+Rωd)=u+d

(1)

其中,ωe为卫星姿态误差角速度，ωd为卫星姿态期望角速度.J为卫星的转动惯量矩阵，且J为实正定对称矩阵，u为控制力矩，d为外部干扰力矩.期望姿态四元数为qd,期望角速度为ωd,误差四元数qe:

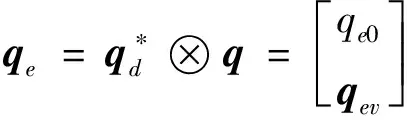
(2)

R是由误差坐标系到惯性系的转换矩阵，给出R关于qe的表达式：

(3)

其中I3为3×3的单位矩阵.误差角速度ωe定义为

ωe=ω-R(qe)ωd

(4)

(5)

考虑到在实际控制中转动惯量矩阵不可能精确已知，故假定

(6)

误差四元数的运动学模型为

(7)

(8)

2 PD+姿态跟踪控制器

一般来说卫星姿态跟踪的PD控制器往往由比例项、微分项构成，二者可以通过星敏感器、红外地平仪、太阳敏感器、陀螺仪等敏感装置测量计算得到，同时控制器结构简单、鲁棒性强，因此在航天领域的到了广泛的应用.但经典PD控制器结构固定、参数固定，这也一定程度上限制了系统性能的优化.基于此，本次研究提出的鲁棒PD+控制器结构为

(9)

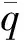
(10)

(11)

(12)

(13)

(14)

为使得滑模面切换点处角速度不发生突变，k1、k2应满足

(15)

在式(11)与(13)中，λ为正常数且满足

(16)

设计控制增益因子ρi,使控制力矩不超过系统上界，ρi定义：

(17)

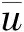
在给出本文控制器结构之后，接下来将给出控制器(9)的稳定性证明与性能分析.

2.1 控制器稳定性证明

为证明系统在控制器(9)作用下的稳定性，首先需要给出两个引理.

引理1.对于任意的正常数kd、kp和三维向量r,系统(1)、(7)、(8)在如下结构的控制器作用下一致渐近稳定.

(18)

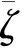
证明.选取Lyapunov函数：

(19)

J是正定矩阵，所以式(19)第一项正定，而kp为正常数，且qe0∈[-1,1],故第二项也正定.有V1>0成立.

对式(19)求导并代入控制器(18)可以得到

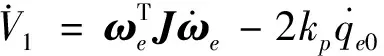
J(ωe+Rωd)-λ‖ωe‖‖ωe+Rωd‖2+

(20)

引理 2.通过选择合适的控制参数，系统(1)、(7)在如下结构的控制器作用下一致渐近稳定.

(21)

se=ωe+kqev

(22)

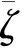
证明.选择Lyapunov函数：

(23)

注意到

(24)

从而有

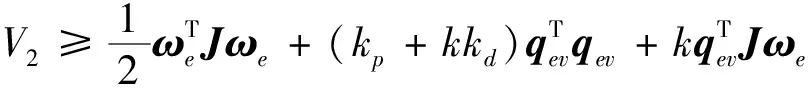
(25)

从而只需满足:

(26)

即可保证V2正定.

计算V2的导数并代入控制器(21)可以得到

(27)

选择参数使得式(28)成立:

(28)

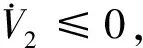
(29)

从而控制器(9)在第二阶段的微分项可以视为

(30)

考虑到引理2中的约束条件，同时注意到

(31)

(32)

(33)

即可使得控制器(9)的第二阶段满足引理2中的约束条件，从而系统在控制器(9)第二阶段的作用下一致渐近稳定.

综上，系统稳定性证明完毕.

2.2 控制器性能分析

本文所提出的控制器(9)能够使得系统状态沿着滑模面(14)运行，从而实现系统收敛速率的提升.

选取Lyapunov函数如下：

(34)

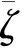
(ωe+Rωd)×J(ωe+Rωd))+

(35)

在控制器(9)的α>‖qev‖≥β阶段对V4求导，并代入控制器(9)，可以得到

(ωe+Rωd)×J(ωe+Rωd))+

(36)

由(35)、(36)可以得到滑模状态se一致渐近稳定.从而系统在控制器(9)作用下能够沿着滑模面(14)运行.同时值得注意的是滑模面(14)分为两阶段，在第一阶段姿态角速度为匀速，这就避免了传统PD控制律中角速度下降过快导致的四元数收敛速率变慢的问题.同时，在滑模面的第二阶段收敛速率为指数收敛，选择合适的控制参数即可实现对于收敛时间的估计.

3 数值分析

ω(t0)=[0 0 -0.08]Trad/s,

ωd(t0)=[0.005 0 0]Trad/s,

qd(t0)=[1 0 0 0]T

(37)

为说明本文提出控制律的性能，以相同参数的传统PD控制律(38)作为对比

(ωe+Rωd)J(ωe+Rωd)

(38)

首先给出传统PD控制律(38)的仿真图.

由图1与图2可以看到，系统状态收敛时间超过250 s，同时在400 s时误差角速度与误差四元数的稳态精度分别为2×10-5和8×10-4.

接下来给出本次研究所提出的姿态跟踪PD+控制器(9)的仿真曲线.

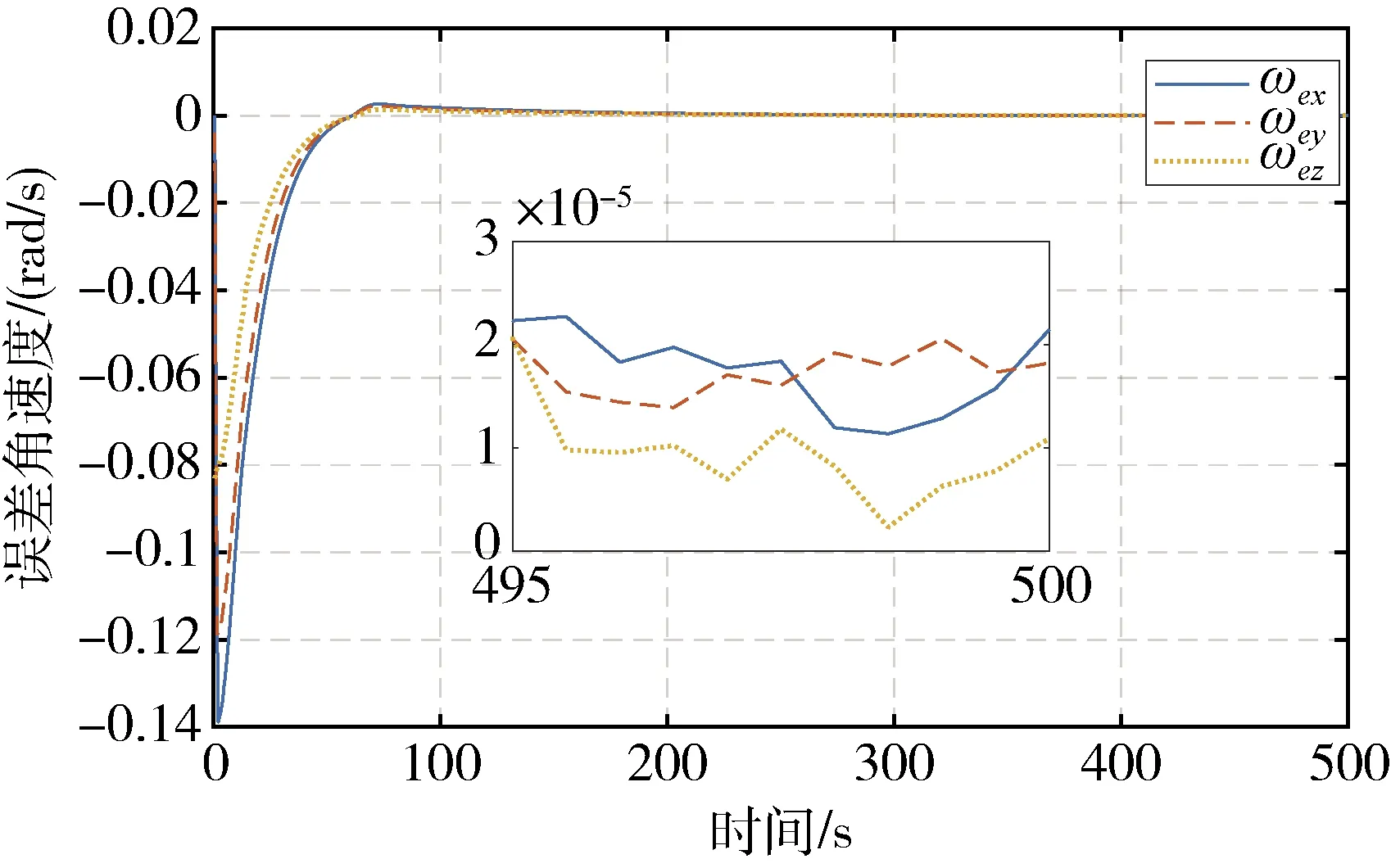
图1 传统控制律的误差角速度曲线

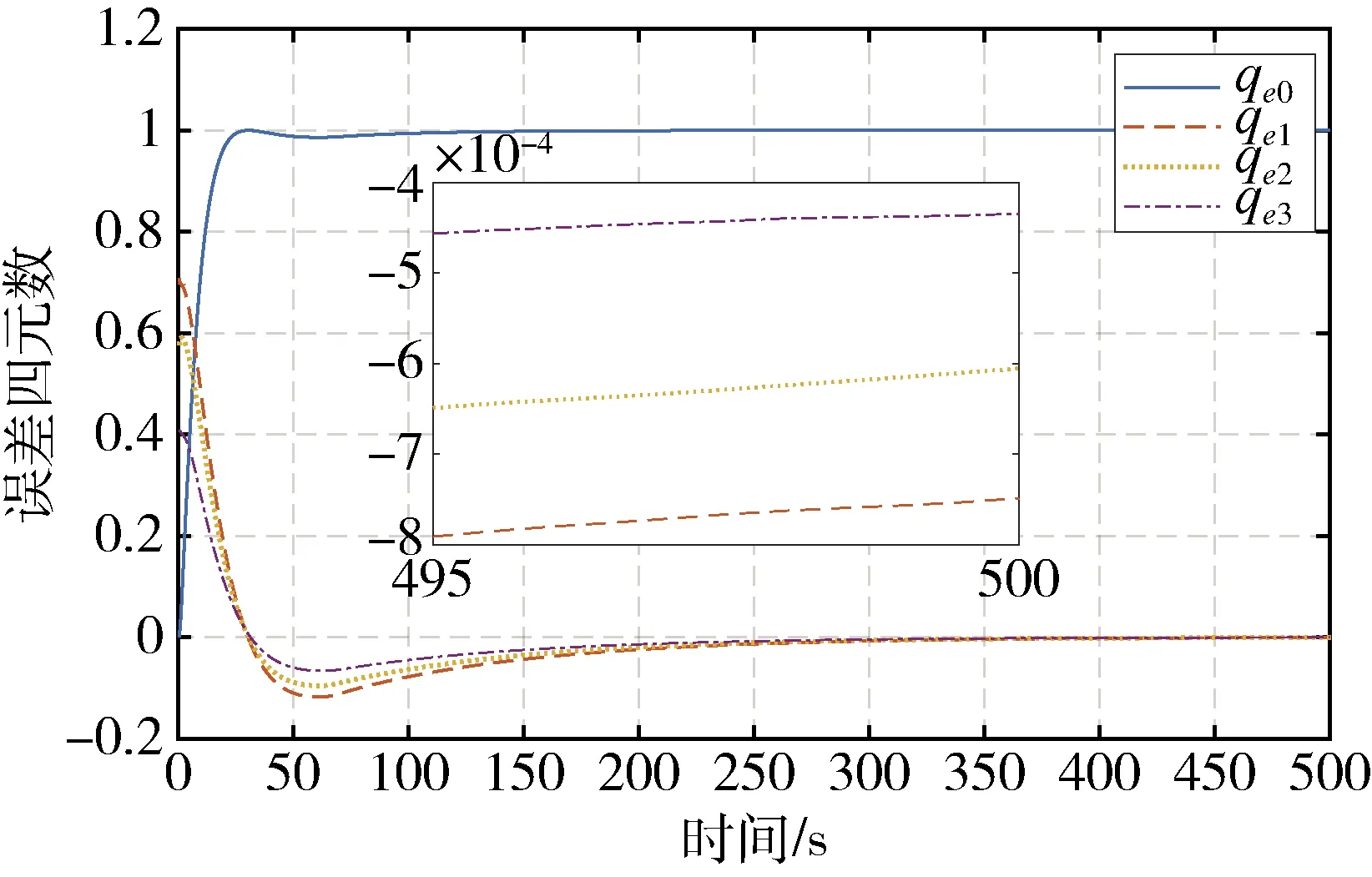
图2 传统控制律的误差四元数曲线

由图3～4可以看到系统在50 s左右收敛，系统收敛时间相比较于经典PD控制器提升约80%，同时在200 s时的误差角速度与误差四元数稳态精度分别为1×10-5和8×10-4，与经典PD控制器在400 s的稳态精度相一致，由此可以认为本次研究所提出的控制器能够在维持稳态精度的前提下大幅提升系统收敛速率.与之前讨论相类似，系统在5 s左右开始进入滑模面(14)的匀速段，在35 s左右开始减速，在此区间内控制力矩维持在相对较小的范围内，这也使得系统对于控制力矩的利用效率得到了提升.

图3 PD+控制器的误差角速度曲线

图4 姿态跟踪PD+控制器的误差四元数曲线

4 结 论

本文面对空间动态目标的跟踪问题，同时针对经典PD控制存在的缺陷，通过滑模控制的思想引入具有优良收敛速率的滑模面，在系统存在模型不确定性、外部干扰的条件下，设计鲁棒PD+控制律实现系统的快速、平稳收敛，实现了收敛速率的大幅度提升.虽然同时控制器结构变得较为复杂，但仍然具有良好的鲁棒性.得出的结论是：在控制器中添加一些辅助项实现PD控制器和滑膜控制的结合，沿着既定轨迹运动，提升收敛速率，同时保持了PD控制器的鲁棒性.