要素错配是否抑制了中国企业对外直接投资的“学习效应”？——基于中国工业企业的微观证据

王紫绮 孔群喜 彭 丹

(1.南京大学，江苏 南京 210093；2.南京财经大学，江苏 南京 210003)

一、引言及文献回顾

中共十九大报告指出，中国经济已由高速增长阶段转向高质量发展阶段。这一对新时代中国经济发展趋势的重大判断表明，中国政府已经开始注重经济发展的质量、效率和效益。因此，如何有效提高企业生产效率成为当今中国经济发展变革的首要问题。与此同时，经济全球化使得发展开放型经济成为全球各国主流选择。在此背景下，中国不断强化“走出去”战略，以持续推动企业对外直接投资(Outward Direct Investment,ODI)发展，并将其作为推进开放型经济高质量发展的一大突破口。自2002年建立对外直接投资统计制度以来，中国企业“走出去”的投资规模不断扩大。2018年，中国全行业对外直接投资额为1298.3亿美元，同比增长4.2%，中国对外直接投资规模已稳居世界前列。进一步来看，在国际形势日趋复杂多变的大环境下，中国企业对外直接投资亦呈现出投资结构多元化、投资方式不断创新、多方合作稳妥有序推进的状态。然而，在取得骄人成绩的背后，在国内制度环境下，资本和劳动力要素市场依然存在着偏向性政策和阻碍要素流动的制度壁垒，现有市场机制下要素无法实现自由流动和有效配置，这给企业投资活动制造了阻碍。因此，在推进开放型经济高质量发展的前提下，如何从要素有效配置角度解决对外直接投资企业生产率低下的问题，这已成为学术界关注的重大问题。

企业通过对外直接投资获得国际上先进的管理经验、技术等，以技术转移机制、技术吸收机制以及规模效应机制获得对外直接投资的学习效应，进而提高本企业的全要素生产率(周超,2018)。从现有文献来看，对于要素错配影响企业对外直接投资“学习效应”的讨论主要从技术进步和规模效应两方面展开。第一，从技术进步角度来看，由于要素错配，技术进步受到严重的抑制，从而阻碍了全要素生产率的提高，进而导致效率损失，削弱了企业对外直接投资的学习效应。Acemoglu(2002)指出，要素的禀赋和价格是诱导技术进步发生变化的根本原因。王亚星等(2017)用TFP作为技术进步的代理指标，研究发现中国要素市场价格扭曲抑制了技术进步。中国部分内资企业所面临的要素价格扭曲问题也十分严重，导致创新资源配置效率提高受到限制，并且影响结构红利的获得(成力为 等,2012)。李永等(2013)对已有垄断竞争模型进行扩展的研究表明，要素价格扭曲会显著抑制国际技术溢出。因此，要素价格扭曲会导致技术溢出和技术创新所需要的市场化“土壤”丧失，那么也就不存在所谓的对外直接投资的学习技术溢出效应。第二，从规模效应角度来看，要素错配所引起的要素价格扭曲会影响企业的生产成本，从而对规模经济效应产生影响。换言之，在要素价格扭曲的情况下，实际规模与潜在规模存在差异。当市场价格扭曲时，实际规模经济基本上都小于潜在的规模经济(Atkinson,1984;Kumbhakar,1992)。朱顺林(2005)的研究也表明，在要素市场扭曲情况下，产业发展中都存在着不同程度的规模效率损失。此外，张雄等(2017)通过对土地资源错配进行研究发现，土地资源要素扭曲程度越大，所导致的经济效率损失就越大。

基于提升对外直接投资企业生产效率的现实需求，本文对要素错配与企业投资学习效应的影响关系进行了理论阐述与实证检验。与现有文献相比，本文可能在以下方面有所贡献：第一，丰富现有理论研究，本文从理论层面论证了对外直接投资学习效应的存在，并揭示了要素错配与企业投资学习效应的影响关系。第二，提升实证检验可信度，由于宏观数据不能有效刻画微观企业对外直接投资与生产率之间的确切关系，因此基于企业角度的分析结果将更加直接和准确；且一般线性回归模型会出现样本选择性偏差，进而引发参数估计内生性等计量问题，本文采用倾向得分匹配法以及双重差分法将有助于减少样本选择性偏误的恶性影响，使研究结论具有较高的可信度。

二、理论分析与研究假设

本文在本地溢出LS模型(1)本地溢出LS模型最早由Baldwin et al.(2001)提出，该模型引入空间因素讨论资本溢出效应的影响，在一定程度上解释了经济增长的 “空间非中性” 特征。的基础上，构建出企业投资学习效应的理论分析框架，尝试从集聚经济的角度，通过分析资本的知识溢出机制以及资本的空间分布状态，以此来讨论ODI企业的“学习效应”以及要素流动对ODI企业“学习效应”的影响。

1.消费者效用

2.生产者利润

本国产品出售到外国时存在“冰山”成本，因此外国消费者获得的本国产品价格是外国消费者消费本国产品价格的τ倍，即p*=τp。工业企业在垄断竞争市场上生产差异化工业品，每个工业企业使用一个单位的新资本作为固定成本，因此新资本的资本收益率就是资本创造部门的经营利润，即π=px/σ。

市场出清时，所有企业的产量和价格均处于均衡水平，此时企业获得零利润。而在垄断竞争条件下，每个企业都采用边际成本加成定价法，因此工业企业的经营利润或资本收益可用下述公式表示。

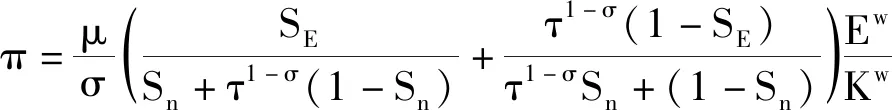
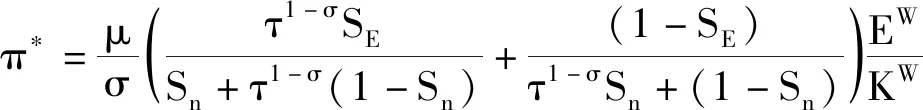
其中，EW表示经济体的总支出；Kw表示总资本存量；SE表示本国相对市场规模；Sn表示本国工业企业总数。

3.均衡结果分析

以本国为例，根据上述的结果可推导出，在对称的长期均衡状态下，本国的相对市场规模为：

当新资本的空间分布主要集中在本国(即Sn>1/2)时，由于dSE/dSn>0，新资本份额的增加将扩大本国的相对市场规模；同时，由于d2SE/d2Sn>0，新资本份额的增加将导致本国的地区相对市场规模以递增的速度扩大。

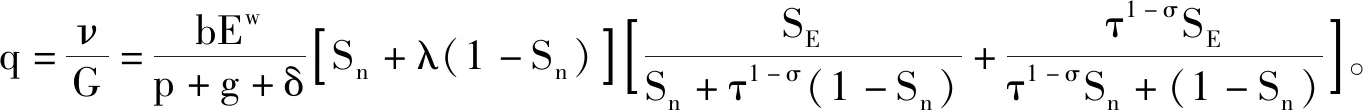
上式中的第一项是需求关联效应。由于0<λ<1、0<φ=τ1-σ<1，故该系数大于零，因此本国相对市场规模的扩大将提升q值，即本国的资本创造成本不断降低，新资本份额不断增加，从而表现为世界范围内的新资本都在本国集聚。第二项是市场拥挤效应，且该系数为负，因此，增加本国的新资本份额会使q值减小，进而导致本国的新资本创造速度不断降低。这是抑制新资本集聚的力量，也是维持新资本在两国之间均衡分布的力量。第三项是资本溢出效应，该系数为正。本国新资本份额的不断增加会导致国内的资本形成成本不断降低，由此提高对新资本的吸引力。因此，国家间知识开放度(即λ值)越低，本地的资本溢出效应越大，本国对新资本的吸引力越强，就越有利于吸引外国的新投资资本向本国集聚。

基于此，我们发现：第一，资本积累主要依靠资本创造部门的学习效应，资本创造过程中的公共知识资本使得当前的资本创造者从过去的资本创造者那里获得好处。具体而言，ODI企业可以通过聘用当地高技能工人和核心技术人才，学习东道国先进技术和管理经验，以寻求战略性资产，从而提升本企业的生产效率(Luo et al.,2007;Lu et al.,2011;Lyles，2014；孔群喜 等,2019)。第二，国际间的资本溢出要比国内的资本溢出受到阻力更大。这也能一定程度上解释下面这一问题：虽然中国企业已成为对外直接投资的活跃主体，但对外投资带来的企业生产率提升效应在短期内效果并不显著，需要有长期的学习积累过程(严兵 等,2016;戴翔,2016;周燕 等,2019)。而在国内要素市场发育还不健全的情况下，中国企业更愿意使用价格低廉的本地中间品，或在本国区际间进行投资，从而减少投资学习效应的途径。因此，根据以上的理论分析，本文提出如下两个研究假说：

研究假说1：ODI企业存在对外直接投资学习效应，即企业通过对外直接投资学习效应提高本企业的生产效率。

研究假设2：在本国要素市场发育不完全时，要素错配会影响企业的投资学习效应，从而抑制本企业生产效率的提升。

三、研究设计

(一)计量模型构建

从理论分析的结果看，企业的对外直接投资行为能够促进其效率水平的提高，而要素错配则抑制了对外直接投资行为带来的学习效应。为了进一步对研究假说进行实证验证，接下来分别构建基准回归模型、交互项模型和差分模型。

第一步，构建基础回归模型，从总体上检验要素错配对企业全要素生产率的影响。要素错配不仅会抑制企业全要素生产率的提升(李平 等,2018)，还会通过加剧技术进步偏向来降低全要素生产率(王卫 等,2018)。因此，在系统地研究要素错配对ODI企业的影响之前，有必要对要素错配与全要素生产率之间的关系进行初步探讨。通常，要素错配包括企业的整体要素错配、劳动要素错配和资本要素错配。因此，在控制影响企业全要素生产率水平的特征变量的情况下，设立基准回归模型，如式(1)—(3)所示：

tfpijt=α0+α1distijt+βXijt+νj+νt+εijt

(1)

tfpijt=c0+c1distLijt+βXijt+νj+νt+εijt

(2)

tfpijt=θ0+θ1distKijt+βXijt+νj+νt+εijt

(3)

式(1)—(3)中，i、j和t分别表示企业、行业和年份；tfpijt是企业全要素生产率；distijt、distLijt和distKijt分别代表企业整体要素错配指数、劳动要素错配指数和资本要素错配指数；α1、c1和θ1衡量总要素错配、劳动要素错配和资本要素错配对全要素生产率的影响；Xijt代表一组控制变量；νj、νt分别为行业效应、年份效应；εijt表示随机扰动项。

第二步，构建交互项模型，有针对性地研究要素错配对ODI生产率效应的作用效果。由于中国ODI企业数量的快速增加，ODI行为和ODI企业已经成为了学者们关注的焦点。同时，通过对现有文献进行整理发现，要素资源的错配或者扭曲会对中国企业的对外直接投资行为以及对外直接投资的技术创新效应产生影响(王文珍 等,2018;姜能鹏 等,2018)。综合考虑之下，本文引入ODI与要素错配的交互项，以分析要素错配对ODI企业全要素生产率究竟会产生怎样的影响。以整体要素错配指数为例，设立模型公式如下：

tfpijt=φ0+φ1distijt+φ2odiijt+φ3distijt×odiijt+βXijt+νj+νt+εijt

(4)

式(4)中，odiijt表示对外直接投资的二元变量；φ3表示要素错配对ODI企业全要素生产率的影响，若φ3<0，说明要素错配会降低ODI的生产率效应，若φ3>0，说明要素错配可以提高ODI的生产率效应。同理可得劳动要素错配、资本要素错配与对外直接投资的交互项模型。

(5)

接下来采用倍差法，将非ODI企业全要素生产率的变动作为参照标准，进而可以衡量对外直接投资行为对企业全要素生产率变动的真实影响。检验企业对外直接投资学习效应的倍差法估计模型如式(6)所示。odi×time的系数即为学习效应，如果γ>0，则表示对外直接投资显著提高了企业的全要素生产率，对外直接投资的学习效应存在；若γ<0，则意味着学习效应不存在。

tfp=β0+β1odi+β2time+γodi×time+ε

(6)

最后，建立双重倍差(Difference-in-Difference，DID)模型，以研究要素错配对企业投资学习效应的影响。此处要素错配是一个虚拟变量dn，主要用以区分要素错配程度。根据总体要素错配指数平均值，把高于平均水平的要素错配企业视为要素错配密集型企业，其他企业视为非要素错配密集型企业。与其他企业相比，如对外直接投资显著提高要素错配密集型企业的全要素生产率，说明要素错配提高了企业的投资学习效应；反之，则抑制了企业的投资学习效应。因此，双重倍差法的处理组是要素错配密集型ODI企业，对照组为非ODI企业和其他类型的ODI企业，对应的计量模型如式(7)所示：

tfp=β0+β1odi+β2dn+β3time+γodi×time+β4dn×time+β5odi×dn+λodi×dn×time+CX+ε

(7)

式(7)中，dn表示区分企业要素错配程度的虚拟变量，要素错配密集型企业取1，其他企业取0；λ系数表示要素错配对企业投资学习效应的影响效果：若λ>0，说明与非ODI企业和其他ODI企业相比，对外直接投资更能够促进要素错配密集型企业全要素生产率的提高；若λ<0，则表示与非ODI企业和其他ODI企业相比，对外直接投资对要素密集型企业全要素生产率的促进作用相对较小，说明要素错配削弱了企业的投资学习效应。同时，odi×time的系数γ反映了ODI对非要素错配密集型企业全要素生产率的影响，该系数大于零，则意味着投资学习效应存在，即与非ODI企业相比，对外直接投资提高了非要素错配密集型企业的全要素生产率。

(二)变量说明

式(1)—(7)中的变量包括：被解释变量、关键解释变量、虚拟变量和其他控制变量。被解释变量是企业全要素生产率，关键解释变量为总体要素错配指数、劳动要素错配指数和资本要素错配指数，用来进行稳健性检验的是劳动价格扭曲指数、资本价格扭曲指数和要素价格扭曲指数。在构建模型的过程中，已经对虚拟变量odi、time和dn进行了详细说明，接下来主要解释本文连续变量的测算方式。

1.被解释变量

企业全要素生产率(tfp)，目前主要有两种常用的方法测度企业层面的全要素生产率，即OP法和LP法。一方面，与LP法相比，OP法使用企业投资作为代理变量，这样将会造成较大的样本损失量；另一方面，对OP法而言，不可观测的全要素生产率变动带来的内生性问题将导致估计偏误，LP法能够更好地将其克服。故而，本文采用LP法测算企业全要素生产率。具体的：(1)使用企业的销售收入衡量实际产出；(2)资本的要素投入主要使用资本存量数据，并根据永续盘存法计算而得，计算公式为：Kit=Ki(t-1)(1-σ)+Iit，Kit、Ki(t-1)分别为当期资本存量、前一期资本存量，Iit为当期投资额，用当期固定资产投资总额表示，即是折旧率，这里依据Wang et al.(2003)做法，取折旧率为5%；(3)用企业的从业人数表示劳动要素投入；(4)采用如下公式计算中间投入：(主营业务成本+销售费用+财务费用+管理费用)-(本期固定资产折旧+劳动者报酬)。

2.关键解释变量

(1)要素错配指数(dist)、劳动要素错配指数(distL)和资本要素错配指数(distK)，由于中国要素错配主要体现为企业获取要素的价格被高估或低估，因此，可以采用要素应得报酬与实际报酬的对比来构建要素错配指数。由于资本要素和劳动要素是影响企业进行投资经营决策的最重要因素，因此本文借鉴Heish et al.(2009)、施炳展等(2012)的做法，使用C-D生产函数来测算资本和劳动的错配指数，而后得到要素错配指数。假设生产函数形式为Y=AKαLβ，Y、K和L分别表示总产出、资本投入和劳动投入，本文分别用工业增加值、固定资产净值年平均额和从业人数表示；A为技术进步；α和β为资本和劳动的产出弹性，二者之和为1，通过对该函数两边取对数，即可将他们求出。进一步地，可得资本和劳动的边际产出分别为：MPK=AαKα-1Lβ=αY/K、MPL=AβKαLβ-1=βY/L。接下来，得到资本要素错配指数、劳动要素错配指数、总体要素错配指数为：distK=MPk/r、distL=MPL/w、dist=distKα/(α+β)distLβ/(α+β)。其中，w为劳动价格，用应付工资总额除以从业人数来表示；r为资本价格，通常使用利率来表示，本文参照盛仕斌等(1999)的做法，采用利息支出与负债合计的比值来测算，得到的利率值若高于0.05，则为资本价格，若利率值小于0.05或者数据缺失，则使用企业各年贷款的平均利率表示资本价格(Hsieh et al.，2009)。此外，在计算过程中，对Y、K和L分别取了对数。

(2)要素价格总扭曲指数(D)、劳动价格扭曲指数(Li)和资本价格扭曲指数(Ki)。为了保证研究结构的准确性，本文还分别使用要素价格总扭曲指数(D)、劳动价格扭曲指数(Li)和资本价格扭曲指数(Ki)来代替要素错配指数(dist)、劳动要素错配指数(distL)和资本要素错配指数(distK)，以进行稳健性检验。借鉴李静等(2012)、李晓龙等(2018)的测度方式，在劳动要素错配指数和资本错配指数的基础上，进一步计算出劳动价格扭曲指数、资本价格扭曲指数，即Li=distL-1、Ki=diskK-1，从而得到要素价格总扭曲指数，具体的计算公式为：D=(1+Ki)α(1+Li)β。

3.控制变量

本文的控制变量包括企业工资水平(Wage)、企业资本密集度(Kl)、企业年龄(Age)、企业融资约束(Finance)和企业规模(Scale)。具体的测算方式分别为：(1)企业工资水平(Wage)，使用应付工资总额除以从业人数表示；(2)企业资本密集度(Kl)，先用固定资产原价减去累计折旧，然后再利用差值除以从业人数来测度；(3)企业年龄(Age)，用当年年份减去开业年份，之后再加1；(4)企业融资约束(Finance)，使用应收账款与企业销售收入之比来表示；(5)企业规模(Scale)，使用资产总额来测度。除了企业年龄之外，本文对控制变量均做对数处理。

(三)样本数据

本文的数据主要有三个来源：第一，2009—2013年中国工业企业数据库数据，该数据库数据不仅包括中国30个省份(除西藏外)所有国有企业以及规模以上非国有企业的基本情况，还涵盖了这些企业的各类财务指标，是较为全面的微观企业数据库；第二，国家商务部记录的《对外直接投资企业(机构)名录》，该名录中含有企业进行对外直接投资的“证书号”、“境内投资主体”、“境外投资企业”和“经营范围”等信息；第三，中国统计年鉴，本文使用的平减指数(如出口品出产价格指数、居民消费物价指数和固定资产投资价格指数等)均来源于中国统计年鉴。

本文的研究样本包括总体样本企业、内资样本企业和外资样本企业、ODI企业和非ODI企业。其中，内资样本企业、外资样本企业是根据企业登记注册类型对总体样本企业进行分类得到的，ODI和非ODI企业则是使用企业的对外直接投资信息进行分类的。本文所使用的企业对外直接投资信息，可以将中国工业企业数据库数据与对外直接投资企业(机构)名录数据进行配对而得到。在对外直接投资企业(机构)名录找到具有对外直接投资行为的企业，然后根据法人单位、年份把这些企业与中国工业企业数据库中的企业进行匹配。本文还对匹配后的样本进行了基本处理，如删除异常值和剔除不符合会计准则的企业样本等，最后共得到376家ODI企业样本。此外，本文使用马氏距离匹配法时配对比例是1∶3，配对变量为企业规模、劳动生产率和企业利润率(Helpman et al.，2004；Hijzen et al.，2011)，共得到了1083家非ODI企业。配对后的ODI企业和非ODI企业在企业规模、劳动生产率和企业利润率变量上不存在明显差异，表明配对效果较好。

四、检验结果与分析

(一)初步观察

1.要素错配状况

根据研究设计的思路，本文分别从投资行为差异、所有制结构差异来分析企业资源错配情况。表1汇报了利用2009—2013年企业数据测算的要素价格错配指数。首先，总体平均要素错配水平显示，中国企业的要素错配程度从2009年1.0426提高到了2013年的16.1823，表明企业普遍存在资本与劳动力价格的扭曲现象，且此要素错配程度呈逐年上升态势。造成要素错配的来源因素错综复杂，诸如企业所有制性质、企业规模、行业属性等。其次，从投资行为差异来看，ODI企业的要素错配情况要优于非ODI企业，其中，2009—2010年ODI企业要素价格存在正向扭曲，此后要素价格出现负向扭曲(2)根据Hsieh et al.(2009)、施炳展等(2012)的研究，如果要素价格扭曲指数取值大于1，意味着该要素的应得报酬大于实际所得，价格被负向扭曲；反之，要素价格被正向扭曲。，且程度不断加深。原因可能在于：企业对外直接投资获得逆向技术溢出，从而提高了资源利用率，减弱了要素错配的程度。此外，从企业登记注册类型来区分，外资企业的要素错配水平略高于内资企业，尤其2012—2013年两类企业的要素配置效率水平差异在不断拉大。出现这一现象的潜在原因是：一方面，中国政府为了吸引外资而颁布各项对外资企业优惠政策，政策性优惠歧视加剧了资源错配的情况；另一方面，外资企业在中国生产、销售一般会受到不公平的对待，且对中国消费者需求也较不熟悉，因而资源分布比例会更加失衡。

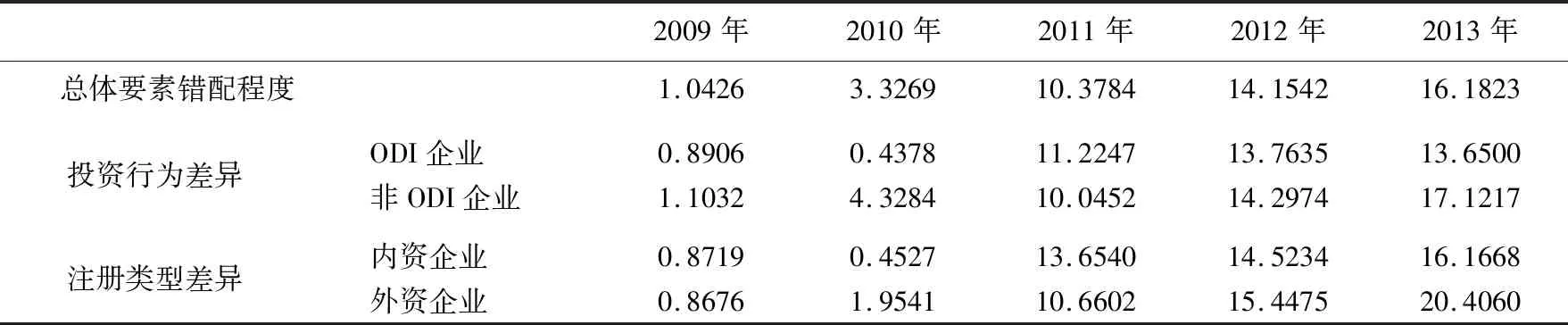
表1 各年份中国企业的要素错配情况

注：作者整理。

2.投资学习效应

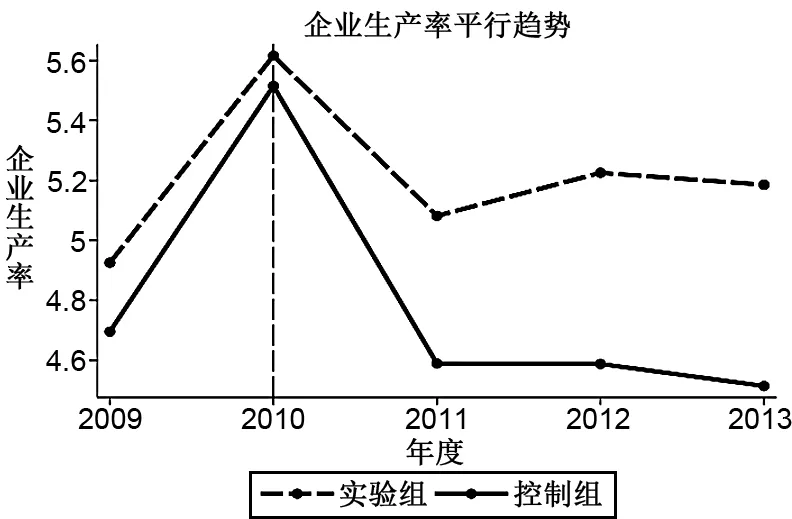
图1 ODI企业与非ODI企业的生产率差异

为进一步考察企业对外直接投资对于其自身生产率的作用关系，即检验ODI是否存在学习效应，本文基于上述实证模型，通过设立实验组与寻找与之相接近的控制组方式，以此来观察ODI行为是否会使企业TFP出现差异，具体可见图1。

从图1可以看出，在进行ODI之前，控制组与实验组企业TFP大致保持相同的增长趋势，同时也表明了实验组和控制组在接受处理之前满足共同趋势假定，这是保证本文进行DID的前提，同时充分表明了本文设立DID模型的适当性。在发生ODI之后，两类企业TFP增长趋势出现明显差异。ODI企业的TFP一直高于非ODI企业，表明对外直接投资存在学习效应。其原因可能是：企业对外直接投资既存在自选择效应(蒋冠宏 等，2014)，又存在学习效应。自选择效应解释了高TFP企业倾向于对外直接投资这一现象，而高TFP企业则可以通过ODI增强自身的创新能力、国际竞争力和获取资源的能力，从而提高生产效率，即对外直接投资能够进一步拉大ODI企业与非ODI企业之间的差距。图1中展现出企业对外直接投资以后ODI企业与非ODI企业之间的差距是非线性扩大的，由此在一定程度上验证了研究假说1。

3.影响趋势分析

为了直观展现要素错配与企业生产率的关系，分别绘制了2010—2013年各年要素错配对企业生产率关系的影响趋势图，具体如图2—5所示。其中，纵坐标是要素错配指数，横坐标是企业生产率，拟合线是要素错配指数对企业生产率的回归线。

从散点图可以看出，2010—2013年要素错配指数大部分是集中于0～20之间，而且扭曲有增强趋势。从回归线来看，该回归线接近水平线，同时具有向下倾斜的趋势，这表明要素错配指数与企业全要素生产率之间大致呈负向非线性关系，与预期一致。多数研究表明，一国生产率的提高得益于要素在不同部门之间合理转移的程度，而要素错配阻碍了经济资源在不同企业之间的再配置，因而限制了生产率的进一步提高。究其原因在于：造成要素错配的来源因素错综复杂，可能包括行业属性、地区特征因素、是否为对外投资企业、是否获得政府补贴等多方面因素。以上研究表明，要素错配抑制了企业的生产效率，但具体的关系仍需进一步探究。

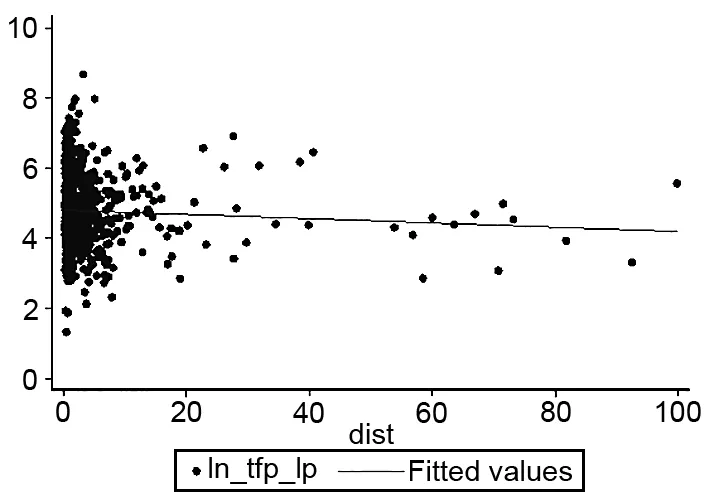
图2 2010年要素错配与企业生产率

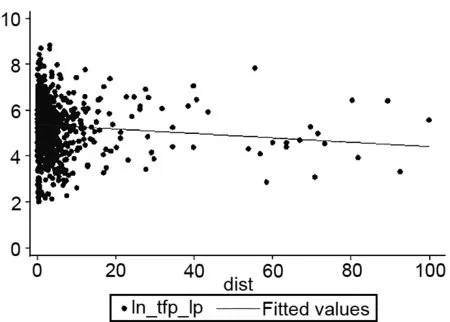
图3 2011年要素错配与企业生产率

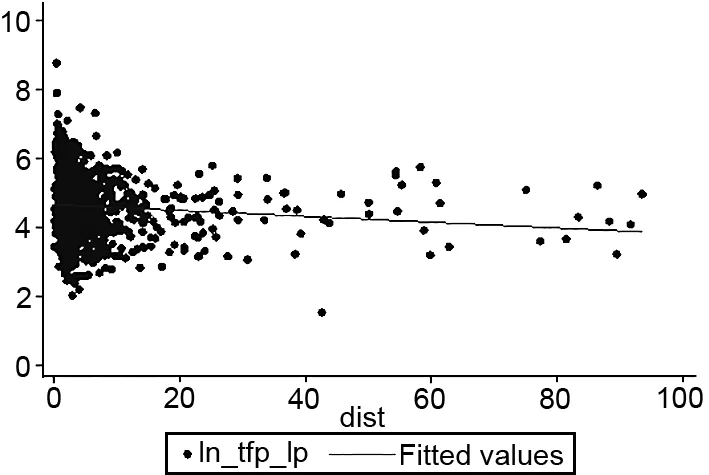
图4 2012年要素错配与企业生产率

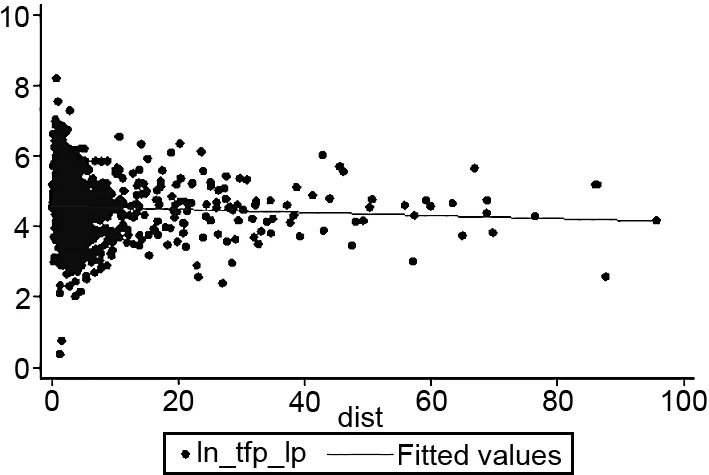
图5 2013年要素错配与企业生产率

(二)要素错配与企业生产效率

1.基准回归检验

为考察要素错配对企业生产效率的影响，接下来分别将全部企业样本、内资企业样本、外资企业样本用OLS方法进行回归，具体结果可见表2和表3。在表2全部企业样本中：列(1)、列(3)和列(5)为未加入交互项时总体要素错配、劳动要素错配和资本要素错配对企业全要素生产率影响的状况；列(2)、列(4)和列(6)为加入交互项后总体要素错配、劳动要素错配和资本要素错配对ODI企业全要素生产率的影响的状况。观察可发现：未加入交互项时，总体要素错配、劳动要素错配和资本要素错配的系数均为负且显著，说明要素错配程度的提升对企业全要素生产率的提高具有显著抑制作用。加入交互项后，总体要素错配、劳动要素错配和资本要素错配的系数均为负且显著，说明要素错配程度提升会显著抑制ODI企业全要素生产率的提高。这是因为：一方面，长期以来，中国城乡二元的经济结构阻碍了人口的自由流动，尤其是高素质人才无法按照市场机制进行相应的配置，致使其创新才能无法得到有效发挥，企业创新生产的效率水平未能得到相应提高；另一方面，近几年来，中国政府对于金融部门信贷决策的干预、“非生产性寻租” 以及政府的创新补贴政策都在一定程度上阻碍了资本市场的自由配置，降低了资本要素的利用效率，从而导致企业生产效率降低。

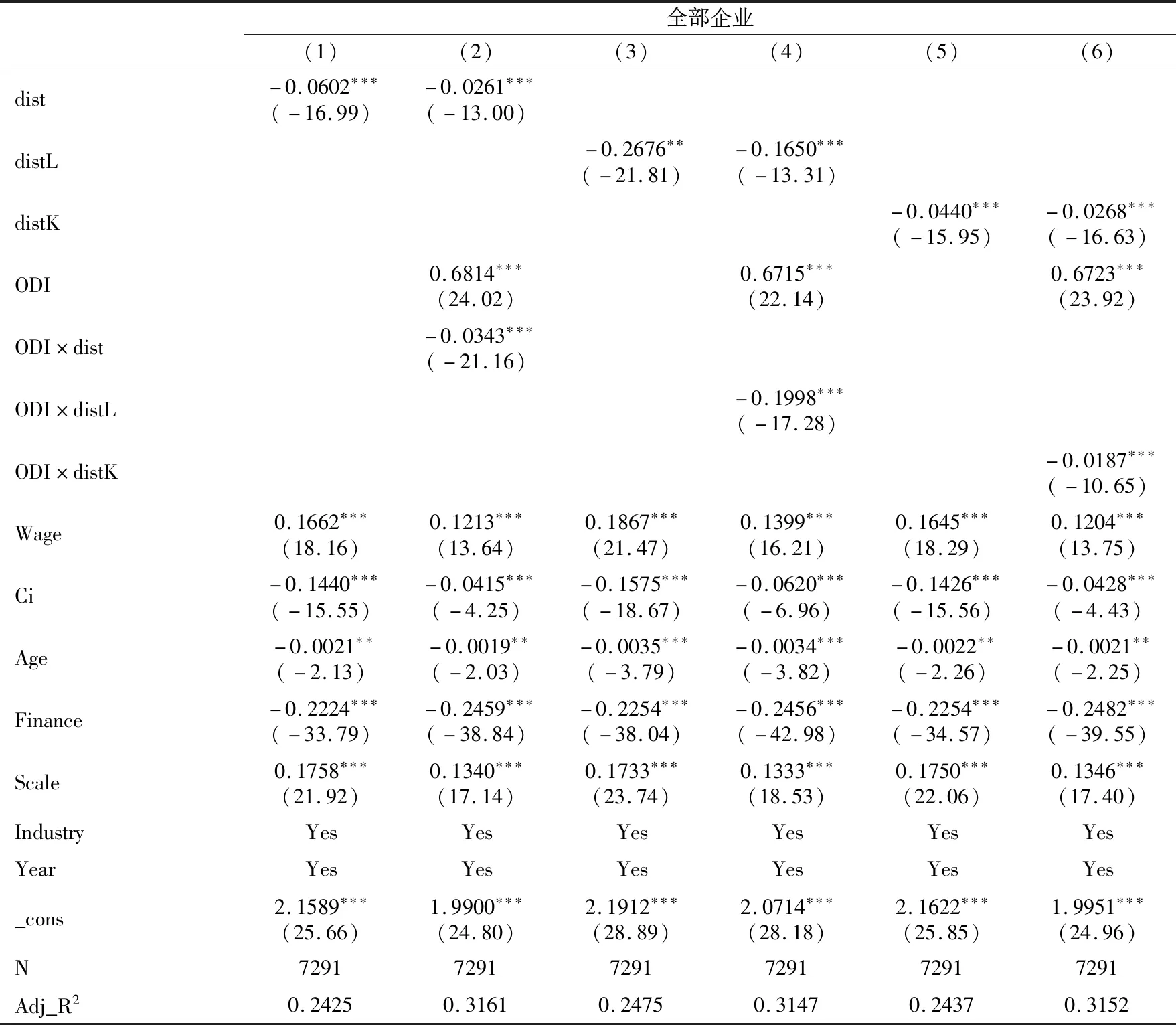
表2 基准回归检验(全样本)

注：dist、distL和distK分别表示总体要素错配、劳动要素错配和资本要素错配；()内数值为相应检验统计量的t值；***、**和*分别表示1%、5%和10%的显著性水平。

表3分样本中，列(7)—(12)是在内资企业和外资企业样本下要素错配对ODI生产率效应的回归结果。观察可发现，在内资企业中，总体要素错配、劳动要素错配和资本要素错配的系数均为负且显著，由此说明要素错配程度的提升对内资企业全要素生产率的提高有显著抑制作用。而在外资企业中，总体要素错配、劳动要素错配和资本要素错配的系数仍为负，但显著性较弱。原因可能在于：外资企业在本土市场中与本土企业深入交流和互动主要借助技术溢出和竞争激励等方式，这有效促进本土企业开展创新生产活动，而对要素需求并不十分迫切，因此，要素错配对企业全要素生产率带来的负面影响较弱(白俊红 等，2016)。

在控制变量中，不论是全部企业，还是内资企业与外资企业，各变量的回归结果均比较稳定，这在一定程度上说明计量方程设定的合理性。对企业生产效率而言，企业工资水平系数显著为正，这说明工资水平的提升对企业生产效率的提高具有显著促进效应；而企业规模显著为正，这说明企业规模的扩大会带来生产效率的提高；企业资本密集度显著为负，这说明资本密集度越高的行业，企业生产效率越低；企业年龄显著为负，这说明企业生产效率会随着企业建立时间增长而不断降低；企业融资约束显著为负，这说明企业融资约束不利于生产效率的提升。

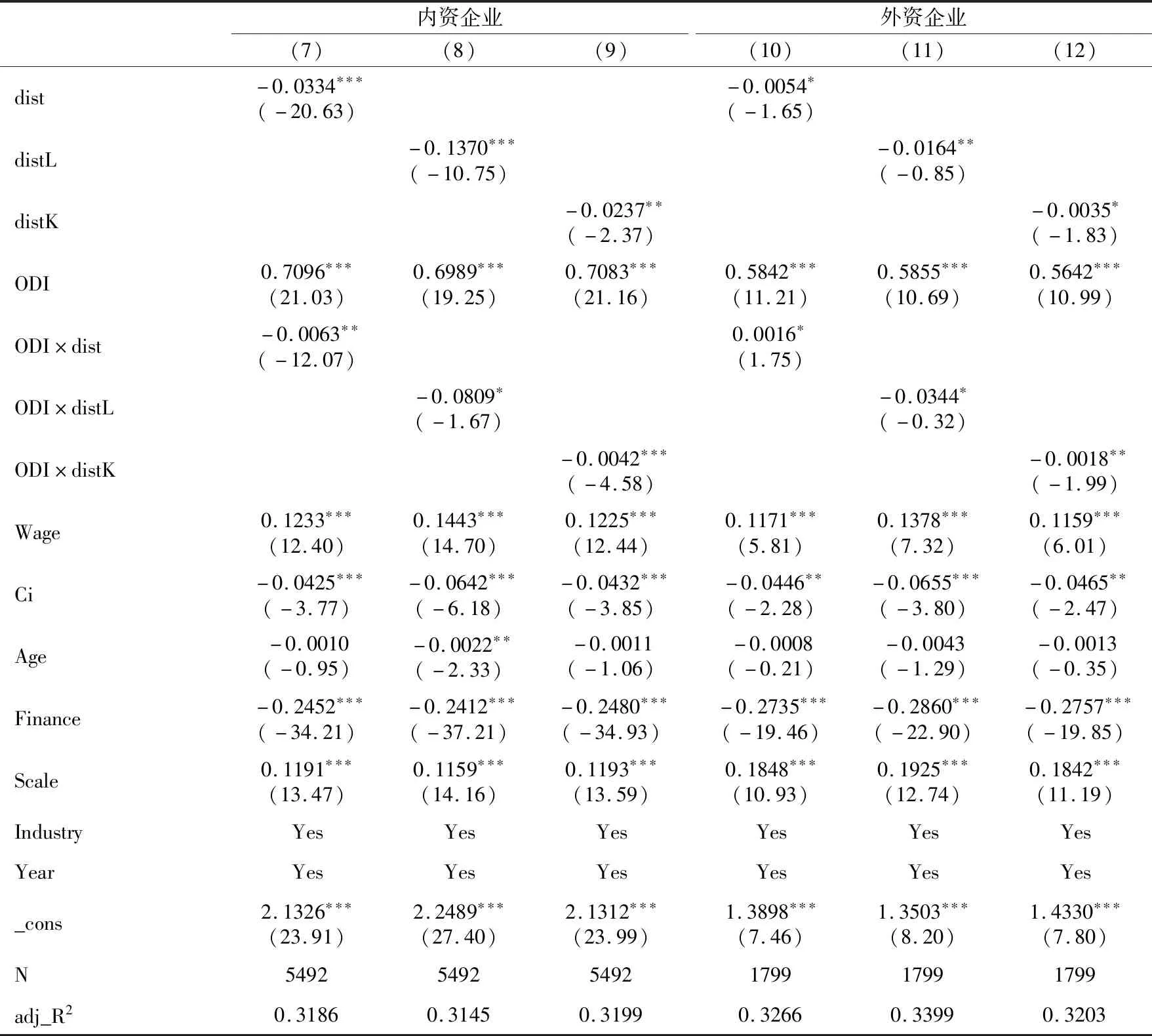
表3 基准回归检验(分样本)

注：dist、distL和distK分别表示总体要素错配、劳动要素错配和资本要素错配；()内数值为相应检验统计量的t值；***、**和*分别表示1%、5%和10%的显著性水平。

2.内生性讨论

考虑到本文的关键解释变量(总体错配指数dist、劳动要素错配distL、资本要素错配distK)可能是内生的，由此会引致内生性问题，为保证本文检验结果的无偏性和有效性，本文采用工具变量(IV)法对关键解释变量的内生性问题进行控制。在工具变量的选择上，本文分别选取内生变量的一阶滞后项作为工具变量，即总体要素市场扭曲、劳动力要素市场扭曲和资本要素市场扭曲的一阶滞后项作为其自身的工具变量，并使用2SLS估计原模型，具体结果见表4。表4中的列(1)、列(3)、列(5)是未加入交互项的估计结果，其他各列是加入交互项的估计结果。从表4中可以看出，所有模型用“不可识别检验”的Anderson canon corr.LM统计值在1%的水平上拒绝了原假设，表明本文设定的工具变量是可识别的。进一步地，本文所关注的关键解释变量的回归结果与表2、表3估计结果基本一致，验证了要素错配与企业全要素生产率间存在相关关系。这些足以证明上文的估计结果是稳健的，在统计上不存在内生性问题。

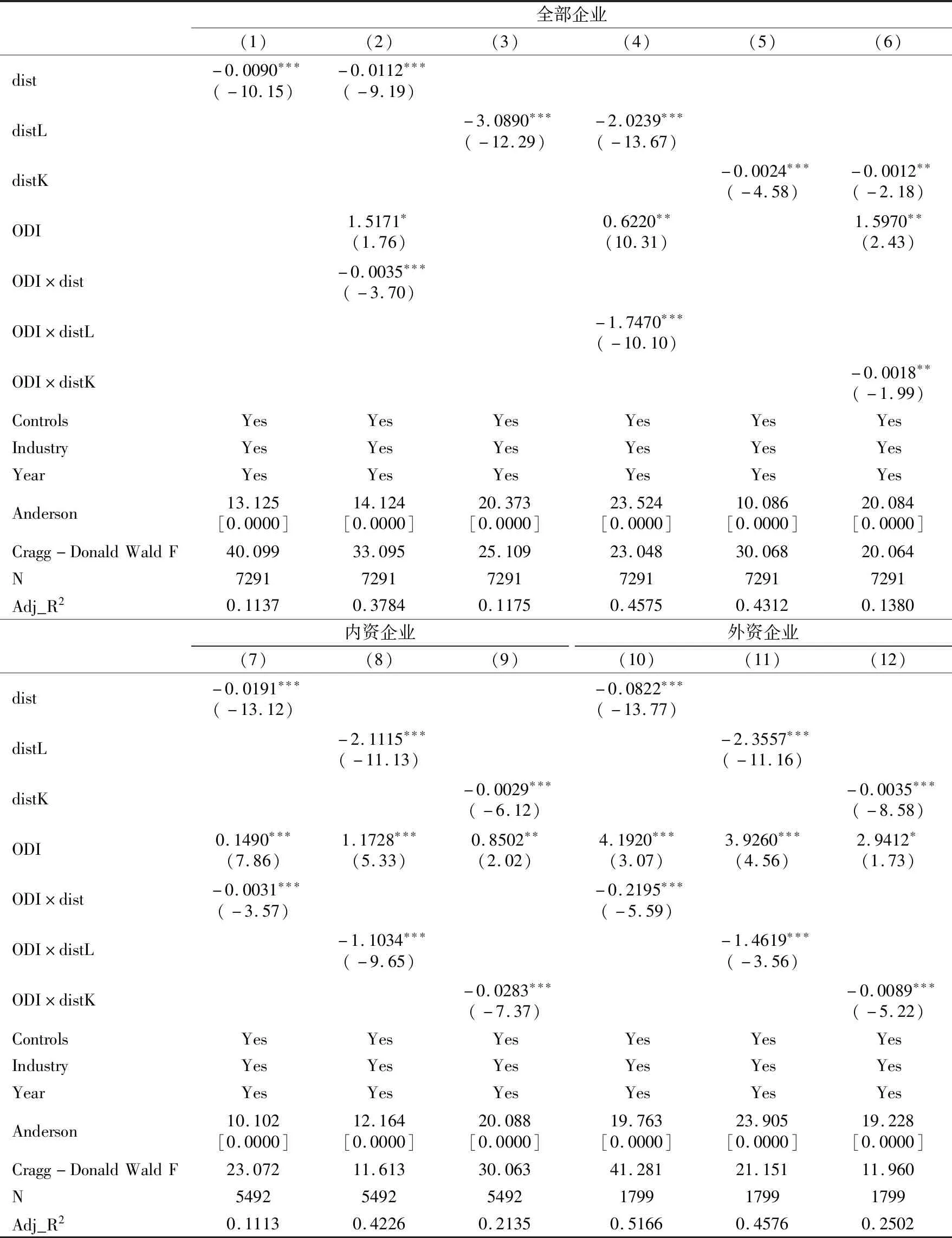
表4 内生性讨论

注：Anderson正则相关性检验的原假设是“工具变量识别不足”，若拒绝原假设，则说明工具变量是可识别的；Cragg-Donald Wald F检验的原假设是“工具变量为弱识别”，若拒绝原假设，则说明工具变量是合理的；()内数值为相应检验统计量的t值；***、**和*分别表示1%、5%和10%的显著性水平。

3.稳健性检验

为检验数据分析的稳健性，本文通过替换关键解释变量的测算方式重新考察要素错配与企业生产率之间的关系。本节使用要素价格总扭曲指数(D)、劳动价格扭曲指数(Li)和资本价格扭曲指数(Ki)来替换模型中的dist、distL和distK，并对模型进行重新估计，得到的结果见表5所示。就非ODI企业而言，D、Li、Ki的系数数值均显著为负，说明要素价格扭曲抑制了企业生产率的提高；就ODI企业而言，不论是全部企业样本，还是内资企业样本或者外资企业样本，ODI系数均显著为正，而D、Li、Ki与ODI的交互项均为负，且都通过了1%的显著性水平检验，说明企业对外直接投资能够对企业生产率的提升有积极的促进作用，但是要素价格扭曲削弱了对外直接投资对企业生产率的积极作用，从而不利于企业生产率的提升，这与上文研究结论一致。以上稳健性检验表明，各关键解释变量的相关系数符号以及显著性与上文研究结论相比并没有发生本质性的变化，说明上述研究结论是稳健的。

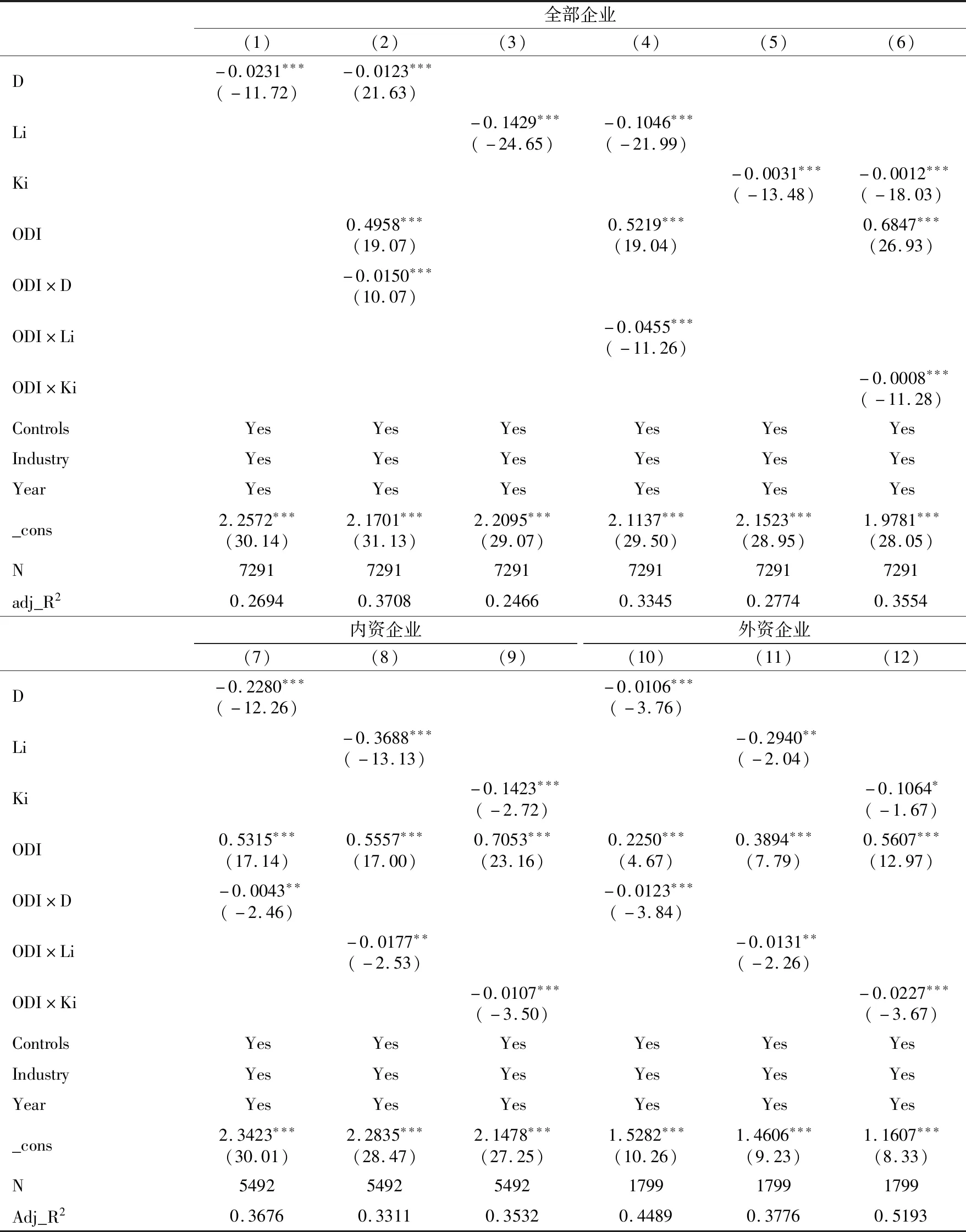
表5 稳健性检验

注：()内数值为相应检验统计量的t值；***、**和*分别表示1%、5%和10%的显著性水平。

(三)要素错配与企业投资学习效应

1.双重倍差估计结果

本文采用1∶3的马氏距离匹配法得到研究样本，使用倍差法以及双重倍差法对要素错配及企业的投资学习效应的关系进行检验，检验结果如表6所示。为控制样本因时间期限不同而导致的偏差以及检验学习效应的动态持续性，表6分别汇报了以2011年、2012年、2013年为期末年份的估计结果，列(1)是倍差法估计结果，列(2)—(3)是双重倍差法估计结果，列(2)未包含控制变量，列(3)加入了控制变量，列(4)—(5)则加入控制变量进行估计。

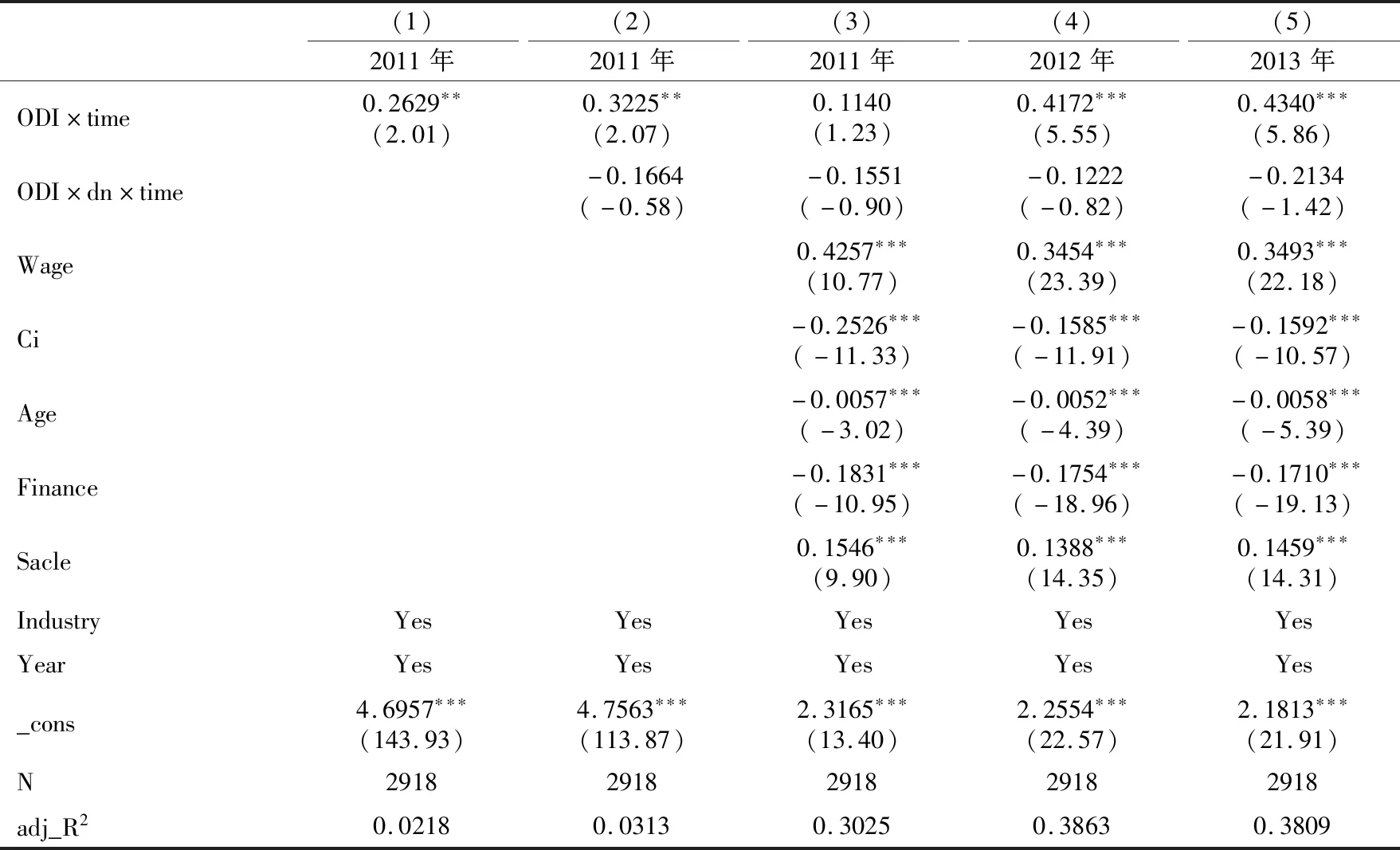
表6 要素错配与企业投资学习效应

注：ODI代表是否为对外直接投资企业，dn代表是否为资源错配型企业；()内数值为纠正了异方差后的t统计量；***、**和*分别表示1%、5%和10%的显著性水平。

表6估计结果显示：从静态时间来看，以2011年为期末年份时，列(1)中ODI×time系数为0.2696，在10%水平下显著，这表明，相较于非ODI企业，ODI企业显著提升了自身TFP，从而验证了ODI存在学习效应，由此验证了研究假说1；列(2)—(3)中ODI×time系数仍然为正，表明对于非要素错配型企业而言，企业能通过ODI行为提升自身生产率，存在投资学习效应；ODI×dn×time系数为负，表明ODI行为对要素错配型企业生产率的作用要弱于其对非要素错配型企业生产率的影响，要素错配削弱了投资学习效应。可能的原因是：一方面，多数研究表明，要素价格扭曲直接影响要素配置效率，而要素价格扭曲所带来的企业间低成本竞争，削弱了企业研发和创新的积极性，从而降低企业从ODI中学习、吸收新知识或模仿先进技术能力；另一方面，要素市场发育不健全时，企业可能会依赖政府来获得劳动、资金等稀缺要素资源，以获得经济租。然而，企业可能会为了获得经济租而将一部分经济资源从生产性活动中转移出来，相应“挤出”企业的研发创新投资，进而阻碍ODI的学习效应，从而证明了研究假说2。以2012年、2013年为期末年份的估计结果与列(3)相类似，与本文预期结果一致。从动态持续性来看，2010—2013年ODI×time系数呈现较为明显的增长趋势，说明企业通过ODI获得的学习效应在持续提升；与此同时，ODI×dn×time系数始终为负，且绝对值一直在提高，表明要素错配对投资学习效应的负向影响愈加明显。可能的原因是：自2009年至今，尤其是“一带一路”倡议推进之后，中国作为对外直接投资大国的地位已经确立，相应地，在激烈的国际竞争中，企业对外直接投资的学习效应也在逐步增强。反之，ODI的学习效应吸引了较多企业进行对外直接投资，这样往复循环进一步拉大了企业之间的差距，加剧了资源错配程度，导致要素错配对投资学习效应的负向影响进一步升级。因此，研究假说1和研究假说2得到了进一步证明。

2.异质性分析：企业所有制差异

以上分析表明，ODI企业存在投资学习效应，但要素错配会对其产生不利影响，但是进一步从企业异质性角度来看，要素错配对投资学习效应的影响是否会因企业所有制的不同而存在差异呢？基于此，本文依据企业登记注册类型，将样本划分为内资企业与外资企业两类，并基于倍差法以及双重倍差法进行了检验，检验结果见表7。表7分别以2011年、2012年、2013年为期末年份，同时显示了加入控制变量后的估计结果。

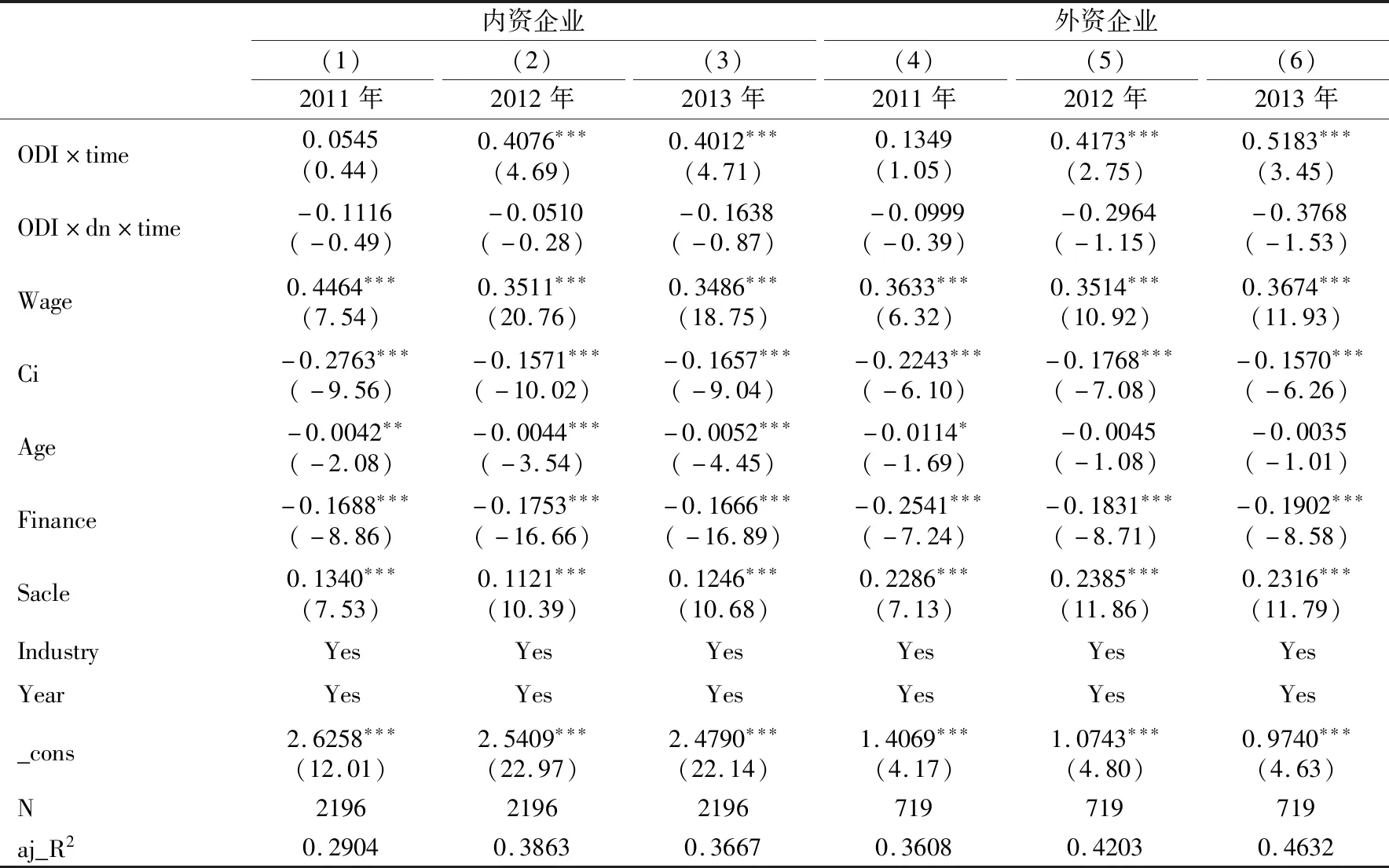
表7 内资企业和外资企业

注：同表6。

根据表7的结果显示，首先，比较内资企业和外资企业的ODI×time系数。内资企业与外资企业的ODI×time系数均为正，而且除了2011年之外均在10%的水平下显著，但相比而言，外资企业的ODI×time系数更高，表明外资企业的投资学习效应更为显著。原因可能是：外资企业与国外关联较为紧密，通过国际上的交流更有利于外资企业学习。其次，比较内资企业、外资企业ODI×dn×time系数。一方面，内资企业与外资企业的ODI×dn×time系数均为负，再次验证了研究假说2，即要素错配削弱了投资学习效应；另一方面，外资企业ODI×dn×time系数绝对值要高过内资企业，表明要素错配对外资企业投资学习效应的削弱程度更深。原因可能是，要素市场扭曲显著削弱了中国企业的投资学习效应，与其他企业相比，外资企业密集使用价格负向扭曲严重的要素进行生产，而且过于依赖要素低估带来的成本优势，从而导致研发积极性不高，技术水平未能得到快速提升(包群 等，2011)。

3.稳健性检验：不同匹配比例及匹配结果

本文采用倾向评分配对法(Propensity Score Matching，PSM)重新为处理组企业挑选配对企业。该方法先对企业的出口概率进行估测，然后根据内资企业和外资企业估计出的出口概率相近程度进行匹配。表8汇报了选取配对比例是1∶4和1∶1时的估计结果。估计结果显示：ODI×time的估计系数均为正，且基本在10%以上的统计水平上显著，ODI×dn×time的系数或为负向显著或为正向不显著。

本文还利用马氏距离配对法为处理组企业挑选最合适的对照组样本。对于处理组企业i∈{Dit=1}与对照组企业j∈{Dit=0}，i与j间的距离为dij=(Ui-Uj)×C1×(Ui-Uj)，其中Ui和Uj为i和j的匹配向量，C为处理组与对照组各匹配变量的协方差矩阵。因此，对于处理组企业i，只有与其距离dij最小的一个或几个对照组企业才能被选为新的对照组企业样本。表9汇报了选取配对比例是1∶4和1∶1时的估计结果。估计结果显示：ODI×time的估计系数均为正，且基本在10%以上的统计水平上显著，ODI×dn×time的系数均为负。表9与表8的结果基本一致，说明本文结论的可靠和稳健。

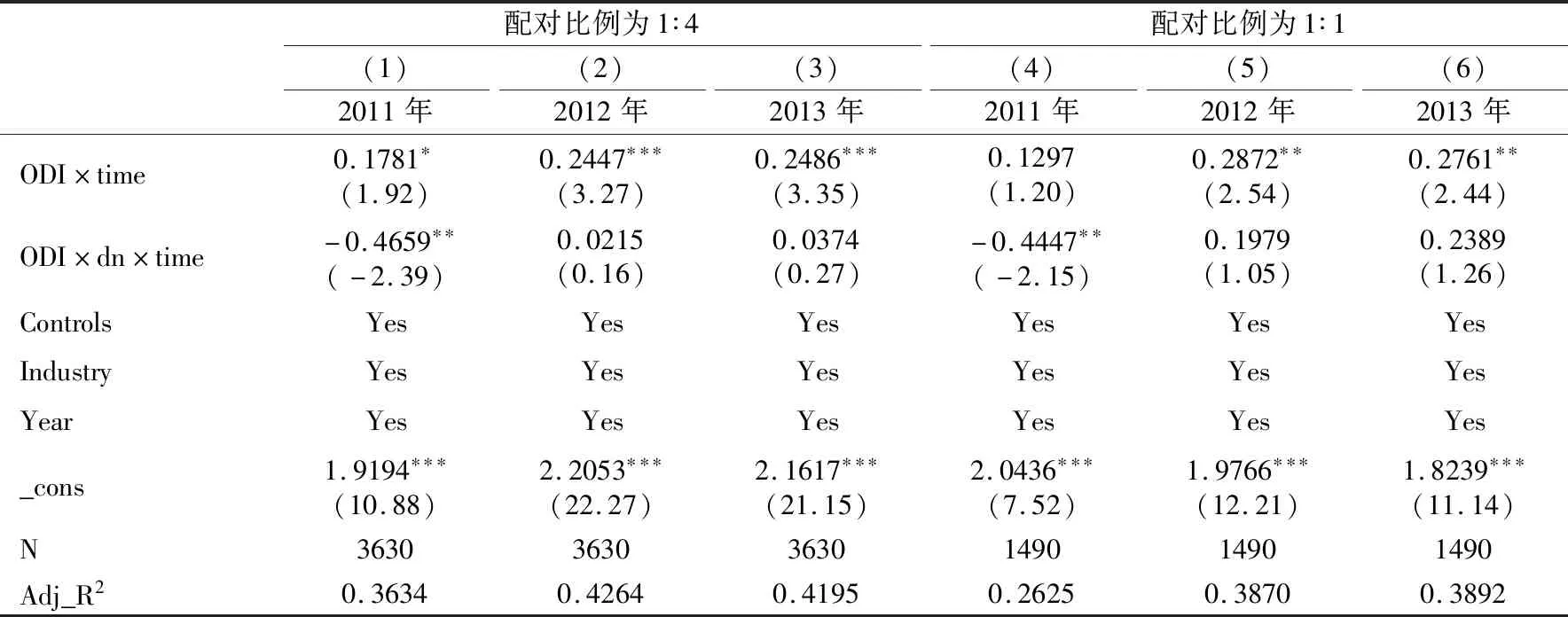
表8 不同倾向得分匹配比例的估计结果

注：同表6。

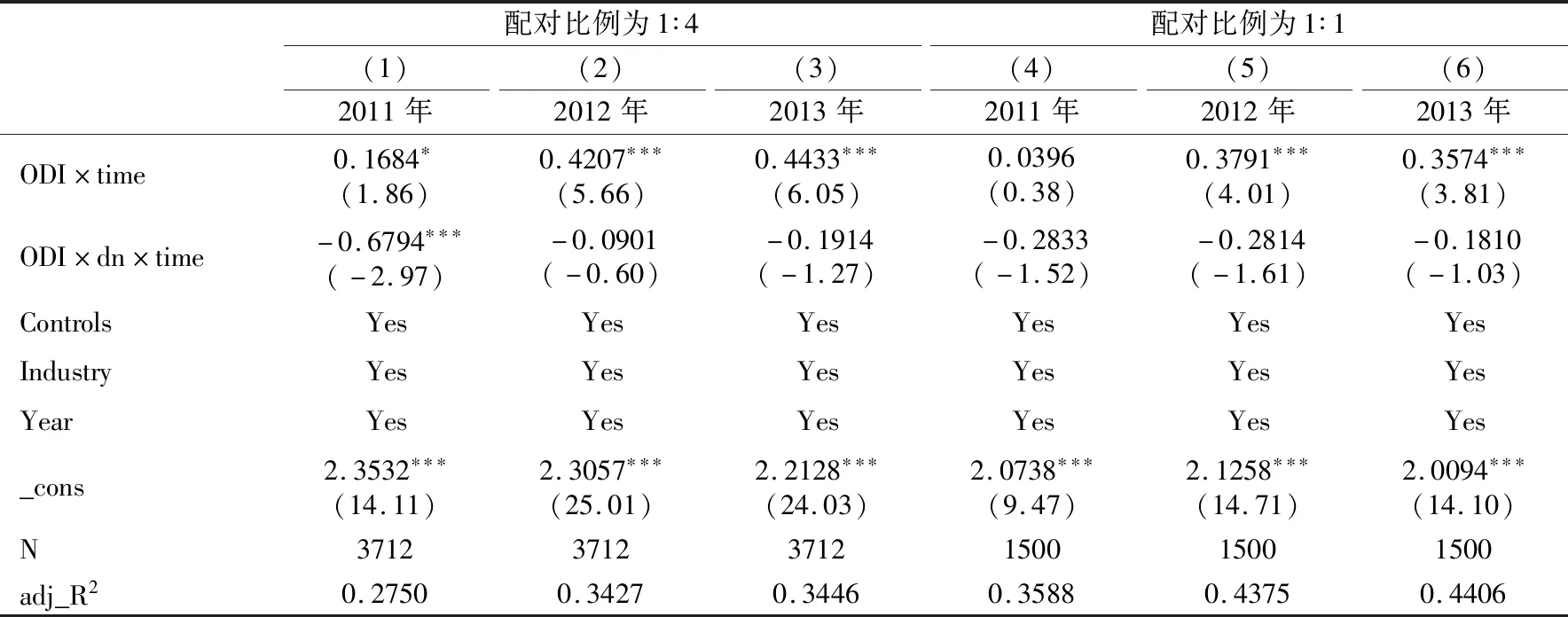
表9 马氏匹配的估计结果

注：同表6。

根据表8和表9的估计结果，ODI×time系数符号均为正，且大部分至少通过了10%的显著性水平，说明对外直接投资显著提高了非要素价格密集扭曲型企业的生产效率，即一般意义上的投资学习效应成立(刘竹青 等，2017)；ODI×dn×time的系数负向显著或正向不显著，说明与非要素价格密集扭曲型企业相比，要素扭曲抑制了投资学习效应。由此可以得出以下结论：不论改变配对方法还是配对比例，均能有效验证要素错配抑制了对外直接投资过程中的学习效应这一结论。

五、结论和政策建议

在中国企业大规模“走出去”的背景下，如何从要素有效配置层面解决对外直接投资企业生产率低下问题，已成为推动开放型经济高质量发展的一大关注点。本文基于2009—2013年的中国工业企业数据库数据与对外直接投资企业(机构)名录相匹配的统计数据，利用企业全要素生产率的影响机制，实证检验了企业投资学习效应的存在性，并探讨了要素扭曲对学习效应的影响。首先，根据本地溢出LS模型，构建了企业投资学习效应的理论分析框架；其次，根据数据匹配方法为ODI企业寻找了可供比较的对照组，并利用倍差法和双重倍差法进行了实证分析。得到结论如下：第一，中国企业普遍存在资本与劳动力价格扭曲，并且要素错配程度在逐年加深；企业进行对外直接投资后的全要素生产率与非ODI企业差距呈非线性扩大，初步证明了投资学习效应的存在性。第二，要素错配会对企业全要素生产率产生不利影响，且要素错配程度加深会显著抑制ODI企业全要素生产率的提高。第三，从静态时间来看，企业对外直接投资存在显著的学习效应，要素错配削弱了投资学习效应，表现为ODI行为对要素错配型企业全要素生产率的作用要弱于其对非要素错配型企业全要素生产率的影响；从动态持续性来看，企业通过对外投资行为而获得的学习效应在持续提升，但同时要素错配对投资学习效应的负向影响却愈加严重；基于企业异质性角度来看，相较于内资企业，外资企业的投资学习效应更为突出，而且要素错配对外资企业投资学习效应的削弱程度要更深。

根据研究结果，本文提出以下政策建议：由于中国的要素市场化发展相对滞后，劳动力与资本的要素价格出现负向扭曲，从而引发了资源配置效率低下问题，并进一步使得对外直接投资企业的学习效应受到不利影响。要确保要素市场改革落到实处，需要做到如下几点：第一，完善要素市场需要构建完善的竞争性要素市场体系。传统观点将要素市场改革与放松价格管制简单关联，并认为除去政府干预而让市场自由定价，就可以实现生产要素价格的市场化，但是忽略了一些重要前提，例如市场化改革是指竞争性市场的市场化，只有市场主体实现多元化才能确保竞争性市场价格而非垄断价格，因此，要实现真正意义上的竞争性市场化价格，关键在于要素市场的主体不能单一化；再如要素价格市场化的前提是生产要素产权明晰，假若产权不明晰，则所有者利益和外部成本难以体现在要素价格之中，因此产权明晰是生产要素自由流动并进行市场交易的基本前提。第二，各要素市场的情况存在差别，不可一刀切，比如劳动市场改革的主要内容是户籍制度改革，牵涉到既有利益格局的方方面面，相关部门在推进要素市场改革时应区别对待、分类改革、有序推进，不可急于求成。