捕捉学生思维火花,提高课堂学习效果
2020-05-21安丽雅
安丽雅

[摘 要] 课堂是教学的主阵地,教师不仅要善于捕捉学生智慧的火花,发现、重组课堂教学中涌现出来的各种信息,把有价值的信息和问题进行转化,成为教学的闪光点;还要在教学设计时调动学生的积极性,让学生主动参与学习活动,敢于发表自己的想法和见解,从而提高他们的思维能力,从而达到知识的灵活运用、触类旁通的目的.
[关键词] 初中数学;思维火花;有效教学
新课程标准指出:数学教学活动,特别是课堂教学应激发学生兴趣,调动学生的积极性,引发学生思考,鼓励学生的创造性思维. 在现在的课堂教学中,教师不仅仅是一个知识的讲解者,更重要的是学生学习活动的组织者、引导者,以及信息的重组者. 教师不仅要善于捕捉学生智慧的火花,发现、重组课堂教学中涌现出来的各种信息,把有价值的信息和问题进行转化,成为教学的闪光点;还要在教学设计时调动学生的积极性,让学生主动参与学习活动,敢于发表自己的想法和见解,从而提高他们的思维能力,达到知识的灵活运用、触类旁通的目的.
教师在课堂上要善于捕捉学生的思维火花,因势利导,完善教学效果
在课堂教学过程中学生往往会有一些突发的灵感,甚至是一些错误的理解,教师是按照自己的教学进度继续讲下去,还是耐心地倾听学生的想法?笔者想大部分教师会选择后者. 因为我们知道学生才是课堂的主体,教师一味地讲解,学生机械地记忆,教学效果会很差. 只有真正让学生的思维动起来,才能达到事半功倍的效果.
第一,利用“一题多解”,激发学生的创新思维,归纳总结选取最优方案. 在一次试卷评讲时,有一道填空的压轴题,当时做出来的学生并不多,因为图形有两次翻折,一看图就觉得很难,很多学生就放弃了.
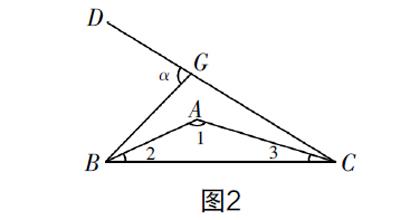
题目如下:如图1,△ABE和△ACD是△ABC分别沿着AB,AC翻折180°形成的,若∠1 ∶ ∠2 ∶ ∠3=28 ∶ 5 ∶ 3,则∠α的度数为______.
本题考查图形的折叠变化及三角形的内角和定理,关键是要理解折叠是一种对称变换. 根据轴对称的性质,折叠前后图形的形状和大小不变,因此可以找到相等的角.
解:如图1,设∠1=28x,∠2=5x,∠3=3x,由∠1+∠2+∠3=180°得28x+5x+3x=180°,解得x=5°,故∠1=28×5°=140°,∠2=5×5°=25°,∠3=3×5°=15°. 因为△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,所以∠BAE=∠DAC=∠1=140°,所以∠DAE=140°×3-360°=60°,所以∠DAB=∠EAC=∠α=80°(根据“8字形”).
当笔者按照自己的思路讲完后,觉得大家都听懂了,就准备讲下一题. 这时有一位学生举手说出她有其他的方法:既然△ABE和△ACD是△ABC分别沿着AB,AC边翻折180°形成的,那么BA,CA就是∠EBC和∠DCB的平分线. 如图2,根据∠1=90°+∠BGC可得∠BGC=100°,则∠α=80°.同学们听完后一个个都表示赞同,课堂里开始活跃了起来,从学生的表情上可以看得出来,这位学生的方法比笔者的简单. 笔者首先表扬了这位积极发言的学生,并从她的解答中受到了启发——还有更简单的方法!于是笔者鼓励其他学生顺着发言同学的思路继续寻找更好的方法. 教室里从兴奋到讨论再到安静,每个学生都希望一鸣惊人. 终于有人举手了:因为BA,CA是∠EBC和∠DCB的平分线,据外角定理得∠α=∠GBC+∠GCB=2∠2+2∠3=80°.此解法更佳!同学们不禁拍手叫好:为什么我们一开始没有想到这个方法呢?于是笔者让每个学生都反思一下,有的说复杂的图形蒙蔽了我们的眼睛,应该在复杂图形中抽象出我们熟悉的基本图形;有的说没有把握轴对称的性质,等等. 学生都表现得非常积极,这一次课堂上的意外反而激发了学生探究的热情,学习效果显而易见.
第二,对学生的思维火花给予正面的引导和鼓励,激发学生的学习兴趣. 数学的课堂如果都是教师在讲解,学生被动接受,那么肯定是枯燥乏味,而且知识容易被遗忘. 怎样才能让一个定理或结论深深地印在学生的脑海里呢?
在上“负整数指数幂的运算”这一课时,已经推导出了公式a-n= ,随后给出一串小题让学生利用该公式计算:-2=______,-3=______,-2=______. 大部分学生按照笔者的要求做完了,但一小部分学生开始嚷嚷,烦分數化简计算量太大了,还容易计算错. 笔者顺势提醒大家看看算出来的结论有什么特点. 小陈同学眼睛一亮,因为-1=2,所以-2=?摇2=22=4,因此公式还可以写为a-n==n. 回答得太漂亮了,这正是笔者所希望的. 为了表示对小陈同学的肯定,笔者模仿书上将这个公式命名为“陈某某公式”,小陈得意极了,其他学生也投来了羡慕的眼神. 以后每次用到这个公式,同学们都会大声地说这是“陈某某公式”,我们班以学生的名字命名的公式和定理便越来越多,大家对这些定理都记忆犹新,大大地提高了课堂学习的效果. 因此鼓励学生发表自己的独特见解,让他们在学习中体验成就感,很大程度上能激发学生的学习兴趣.
第三,巧妙利用学生的错误想法,让学生在错误中反思. 苏霍姆林斯基说过:“教育的技巧并不在于能预见到课的所有细节,而在于根据当时的具体情况,巧妙地在学生中不知不觉地做出相应的变动. ”所以教师要利用课堂上的突发思维,甚至是学生的错误想法转化成课堂上宝贵的教学资源,成为同学们引以为戒的反例,能达到更好的教学效果. 例如,在学习同底数幂的除法时,黑板上出了这样一道题:-y3n+1÷yn+1. 小张学生不假思索地脱口而出:-y2n+2. 下面开始小声议论,有小部分同学表示赞同,也有同学表示反对. 其实这是一个典型的错误,在以往的考试和作业中一直有同学犯类似的错误,这是一个很好的“反面教材”啊. 笔者让小张同学上黑板把他的运算过程写出来:原式=-y3n+1-n+1= -y2n+2. 同学们发现了他的错误,减多项式整体的时候一定不能忘了加上括号. 我们再一起回顾了整式的加减的方法以及去括号的法则,并把这个错误命名为“张某某错误”,每个学生都对“张某某错误”记忆深刻,大大减少了类似错误的发生.
教师的备课要有弹性和开放性,为激发学生的思维火花创造条件
传统的教学过分地强调预设,也就是严格按照教案上课,课堂上要提哪些问题,包括有几个环节,每个环节要用多少时间都是精心计算好的. 所以往往有时开课的时候请学生讨论也是规定时间的,不管学生有没有讨论出结果,或者学生有不同的理解,为了预设的时间,就匆匆进入下一个环节. 这样缺乏对学生好奇心的激励,缺乏学生对问题的钻研,久而久之,学生就会失去学习数学的兴趣了,所以备课要留有余地. 当课堂上出现学生了不同的见解或突发情况,要给学生充分的思考时间,把一个问题研究透彻,鼓励学生表达、纠错,让学生的思维真正活跃起来,往往能收到意想不到的效果.
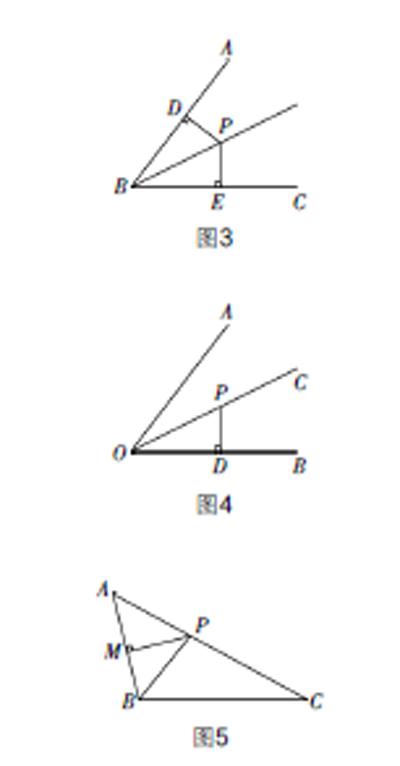
第一,教师在课前要根据班级学生的特点做好充分的准备,要预见到不同层次学生的基础以及学习该知识点的困难所在,激发高水平的精彩的生成. 例如,在“角的轴对称性”的复习课时,笔者把由易到难的几道题串起来进行讲解,收到了不错的效果. 第一步,如图3,先复习角平分线的性质和几何语言的书写;第二步,直接利用性质解决一道基础题,求点P到OB的距离,如图4,并引出常见的辅助线的添法;第三步,如图5,BP为△ABC的角平分线,已知AB,BC的长度直接写出△ABP与△BPC面积的比值;第四步,如图6,已知AC平分∠BAD,判断∠ABC与∠ADC的数量关系. 前三题大部分学生都能很快回答出来,但在第四题上出现了百家争鸣的景象,有的学生受到教师前三题的影响,添出了点C到AB,AD的距离(如图7),也有学生采用了前一章学习的“截长补短”证全等的方法(如图8、图9)解决了问题. 课堂上学生积极发言,思维活跃. 当最后一?摇题题目出现时,学生个个跃跃欲试,都想争做“解题达人”. 题目是:如图10,分别以△ABC的边AB,AC为边向外作等边三角形ABD和ACE,CD与BE相交于点O,判断∠AOD和∠AOE的数量关系并证明. 虽然第四题的图形复杂,但是有了上面题目的启发,还是有不少学生成功地添出了辅助线(如图11),获得了成功的体验. 解题完成以后要让学生归纳总结一下添辅助线的技巧,归根到底是要构造轴对称图形,这样有利于帮助学生克服对难题的恐惧,激发学生探索求知的欲望,达到解决一类题目的目的.
第二,课堂上要留给学生足够思考、讨论的时间,教师是课堂教学的引导者,学生才是课堂教学的主体,教师不能替代学生发现问题,而应该创设情境引导学生发现、归纳结论,激发学生的创新思维. 在上一次函数的应用时,大多数情况都是教师给出题目由学生解答. 为了拓展学生的思维,笔者从学生熟悉的小故事入手,将题目改为开放式的问题,学生一下子就来了兴趣,通过小组PK,比一比哪个组得到的信息最多,哪个小组得到的信息最有价值,哪个小组得到的信息最有难度. 如图12,“龟兔赛跑”是同学们熟悉的寓言故事,图中表示了路程s(m)与时间t(min)之间的函数關系, 请同学们仔细看图,你能从图中获取哪些信息?学生们联系实际,积极思考,得到了很多精彩的答案,大家不仅掌握了一次函数的性质,还对一次函数的应用留下了深刻的印象.
第三,课堂教学是师生双边活动的过程,教学活动的成效在很大程度上取决于师生融洽的程度、了解的程度,教师对学生的影响、学生之间的合作与竞争、班级的学习风气都会对课堂教学产生不容忽视的影响. 良好的课堂学习氛围,教师一个鼓励的眼神,一句表扬,一个提醒,都是学生学习的动力和源泉. 只有让课堂“活”起来,呈现出生机勃勃的精神状态,才能激发学生的思维火花,提高学生的创新能力,从而提升课堂学习的效率.
总之,高质量、高效率的课堂教学是促进学生有效学习的前提,课堂教学目的在于使每一位学生不断地获得新知识和能力,使每一位学生获得最大的进步和发展. 新课程改革提倡向45分钟要效益,这就要求我们每一位教师要立足课堂,以学生为本,实施促进学生有效学习的教学策略,探索促进学生有效学习的教学模式,充分调动学生的学习积极性,激发学生求知探索的欲望,真正地爱上数学、爱上学习.
