全自动驾驶车辆动态包络线理论计算与试验研究

厉 高， 林建辉， 陈双喜

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

铁路限界的研究是一个日趋完善的过程，从最初的结构限界到静态限界再到综合悬挂变形、线路条件等因素的车辆动态包络线，考虑的因素越来越全面[1]。限界的理论计算主要的参照标准有UIC505，德国BOStrab标准，还有国内的CJJ96《地铁限界标准》[2]。邹建军[3]等基于CJJ96《地铁限界标准》对网轨检测车进行了限界计算且开发了相应软件。张晓明等[4]通过Simulink仿真的方法对车辆动态包络线进行了数值仿真。马荣成[5]等基于轨道车辆耦合动力学理论进行了车辆动态包络线计算，但是基于标准与仿真的计算都尚未进行线路试验验证。

针对北京地铁燕房线B1型全自动驾驶车辆。综合车辆结构特征与线路条件选择静态偏移轮廓与动力学仿真偏移的叠加算法确定车辆动态包络线，并进行动态包络线线路试验，对CJJ96《地铁限界标准》与叠加算法、线路试验结果进行了对比分析。解决了公式计算结果过于保守且结果无法验证的问题，为动态包络线的理论计算以及动态包络线线路试验提供参考。

1 车辆动态包络线叠加计算

车辆在平直的轨道上按规定速度运行，考虑轨道几何偏差、车辆的各种振动和滚动等正常状态下运行的各种限定因素，而产生的车辆各部位竖向和横向动态偏移后的统计轨迹，以基准坐标系表示称为动态包络线[6]。基准坐标系的坐标原点为轨距中心点，横向与轨道平面相切，竖向垂直于轨道平面，如图1所示。动态包络线的计算包含了车辆在运行过程中产生的偏移量，能够更加准确，全面的反映

车辆运行姿态，以充分的利用限界空间[7]。

1.1 车辆轮廓控制点的选取

根据车辆设计方案，车体有效长度19 000 mm，中心销定距12 600 mm，端部距相邻中心销的距离为3 200 mm。为了描述车辆的偏移情况，根据车辆的自身结构特点，在车辆上选取控制点，获得车辆轮廓离散坐标。车辆静止于直线轨道上的平衡位置时，车体的计算断面上部取空调位置的断面，两侧取车体两端的截面，车体最下端的截面取车辆底架下的悬挂的设备的最大外围轮廓，图1为选取的全部车辆轮廓控制点。

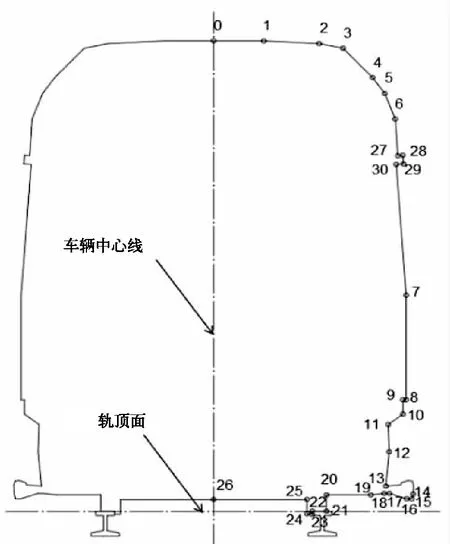
图1 计算基准坐标系与控制点注：0-9，27-30为车体上点，10，11为构架上点，12-20，25，26为弹簧下部件上点，21，22为踏面上点，23，24为轮缘上点。

1.2 静态偏移轮廓计算

静态偏移轮廓主要参照CJJ96《地铁限界标准》计算。计算要素主要有车辆的制造误差，车辆的维修限度，转向架轮对相对于轨道的最不利位置，以及车辆制造载荷不对称等引起的偏斜等。未考虑标准中如悬挂侧滚位移量等与车辆运行工况相关的参数。计算主要分为车体、构架、轮对踏面部分，考虑多种偏移组合方式求取静态偏移轮廓。对于随机因素如安装误差等引起的车辆偏移量采用均方根值合成，对于非随机因素如车体控制点、磨耗等引起的车辆偏移量按线性相加处理。

针对标准中所考虑的过极端情况(如轮轨间隙与悬挂位移均按照极限值选取时，出现的当一侧轮缘已经接触钢轨时，仍考虑该侧横向止挡也到达极限位置)造成计算结果保守的问题。文章对标准中计算公式进行简化，将悬挂动挠度、横向加速度、风压等动态因素去除，以获取静态偏移轮廓，之后叠加动力学仿真偏移量，获取动态包络线。简化后的部分公式如下：

车体横向平移与倾角产生的位移相同时车体横向偏移量：

(1)

车体竖向向上偏移：

(2)

车体竖向偏移向下以及其余部分计算公式修改方式类似，文中不再赘述。上述公式涉及到的部分计算参数如表1所示。

表1 静态计算需求参数(部分)

计算过程中，对于横向位移分为车体横向偏移与倾角产生的偏移方向相同与相反，竖向位移分为向上、向下，共有4种组合，根据控制点位置的不同提前预判将控制点分为4类分别进行计算，如图1所示车体控制点2、3选取为向右上方偏移的点，10、11选取为向左下方偏移的点，其余控制点的情况类似，计算结果将在最后进行展示。

1.3 动态偏移量的计算

在车辆实际运行过程中，侧风、轨道不平顺等对动态偏移量有重要影响。针对这部分动态偏移量，本文采用动力学时域仿真的方法得到车辆振动位移和姿态，能充分考虑侧风、线路条件、车辆参数等因素的耦合影响，模拟车辆运行状态优化动态包络线的计算。

由于车辆位移属于低频信息，故建立多刚体动力学模型即可。笔者采用多体动力学仿真软件SIMPACK，建立42自由度的车辆动力学简化模型如图2所示，进行仿真分析。

图2 42自由度车辆动力学模型

车辆由1个车体、2个构架、4个轮对组成，车体、构架和轮对分别包含纵向、横向、垂向、侧滚、点头和摇头6个运动状态，共计42个自由度。

为充分考虑侧风作用对车体的悬挂偏移量的影响，在仿真过程中，初期不考虑侧风的影响，随后线性添加侧风，风压数值同试验现场风压一致，最后实现稳定的侧风作用。通过在一段时间内添加轨道激励(美国五级谱)仿真横向加速度等相关动态因素，以此来验证模型，车辆控制点位移时间历程如图3所示。通过在模型静态偏移量计算控制点处添加传感器，获取控制点位置信息，并减去车辆静态坐标，获取动态偏移量。将该动态偏移量叠加之前计算的静态偏移轮廓，最终获取车辆动态包络线理论值。

图3 车体横向位移时间历程示意图

2 车辆动态包络线的线路试验

传统的限界门方法[8]，仅仅是通过性测试方法，已经无法满足当前的需求，文中提出了一种基于位移倾角精确检测技术的车辆动态包络线的线路试验方法，通过解析几何算法获取车辆动态包络线。

2.1 试验方法

同理论计算一致，文中试验对象为北京地铁燕房线B1型全自动驾驶车辆，试验载荷状态为AW0、AW3，试验最高速度为80 km/h，车辆按照正常运营模式，到站停车。试验基于位移、倾角精确检测技术，精确测量一系轴箱相对于构架的垂向偏移量，车体相对于构架的垂向偏移量以及车体倾角，结合解析几何算法推算车体动态轮廓。至于车下横向位移补偿部分，通过安装在转向架上的2D激光，扫描轨顶平面下方19 mm处，获取线路中心线以补偿横向位移，补偿原理如图4所示。

图4 激光补偿原理图

理论上车体偏移的极限位置出现在车体的两端面或车体中心截面处。考虑到实际试验传感器安装等因素，选取转向架中心销截面为计算断面，并通过算法补偿断面位置选取的误差，计算断面如图5所示。

在列车车厢地板下方试验截面处安装倾角传感器，获取车辆中心线与轨道中心线相对偏移角度。一系位移传感器固定端安装于一位侧、二位侧轴箱上方。二系位移传感器固定端安装于构架靠近空簧位置，前后转向架对称安装，获取车辆动态包络线。

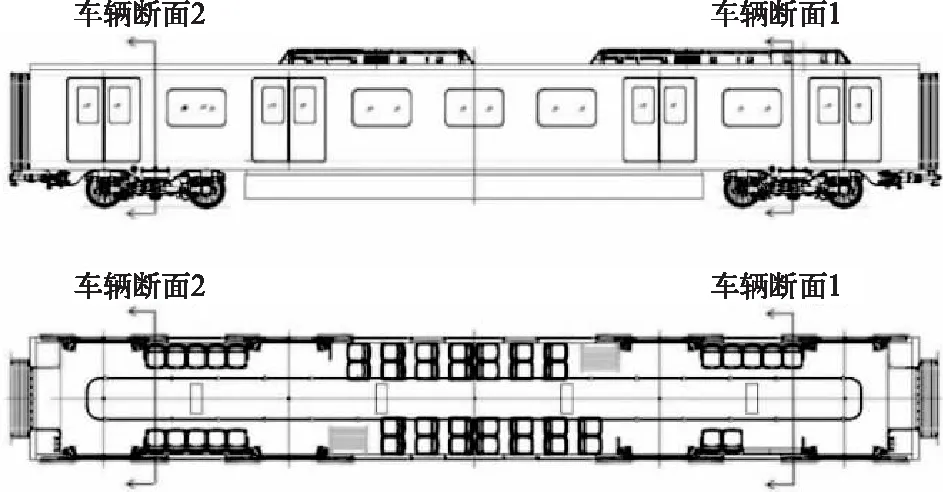
图5 试验断面的选择

2.2 试验动态包络线算法

图6为一位侧拉线位移传感器数据。可以看出，位移数据约560万组，共分为7段与车辆到站停车次数一致。

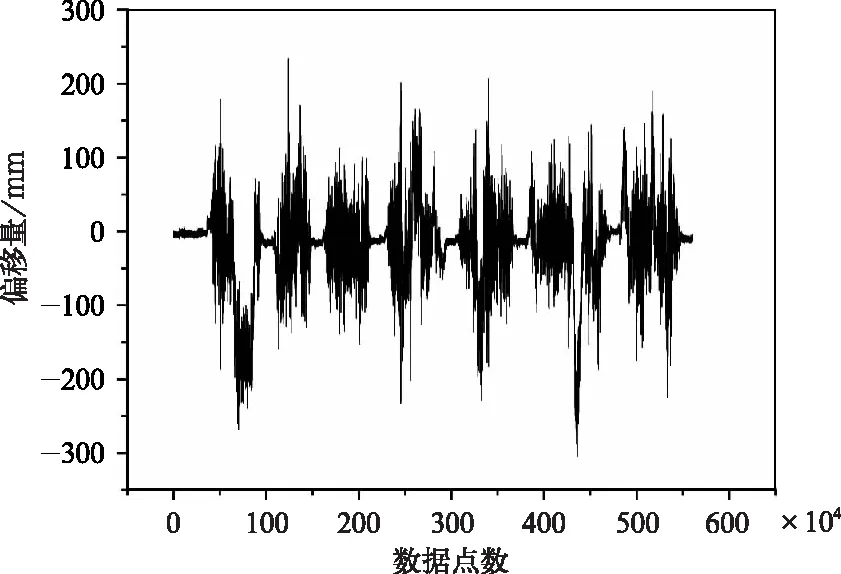
图6 车体控制点0横向位移数据

为消除设备误差、系统误差影响，提高数据有效性。对数据进行截断，去除开头与结尾处5%数据，以保证数据采集设备记录数据的同步性。对截断后的数据进行标准化处理以消除传感器初始安装误差带来的影响，降低数据方差，获取数据的变化趋势，方便后续计算。

算法基于刚体假设，以基准坐标系为基准，利用解析几何方法求解动态包络线。其中车体部分是动态包络线计算的重点，对于由倾角引起的车体偏移量，计算分为倾角向右，向左两种情况，分别采用不同的算法。由于位移的变化为线性变化，满足可加性，故单独计算车体控制点位置的横向与竖向偏移量。

对于车体横向偏移量，由倾角变化所引起的横向偏移量叠加2D补偿偏移量组成。当车体倾角向右时，以车体上某个控制点A(x，y)为例，计算原理见图7。

控制点横向偏移计算公式为：

x′=x+μ(xcosα+ysinα-x+xc)

(3)

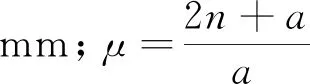
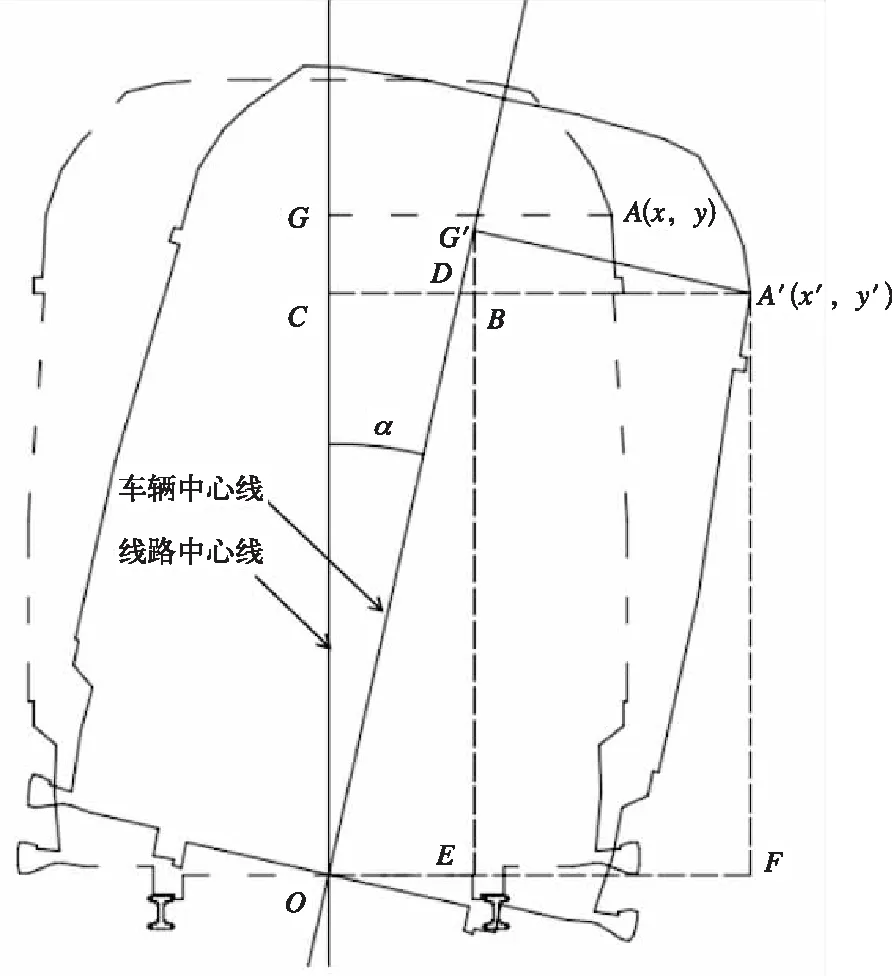
图7 车体倾角向右算法原理

为补偿由截面选取造成的误差，通过观察理论计算公式发现μ多作为权值因子出现。其物理意义为车体长度与车辆定距比值，反映的是车体支撑点与车长之间的关系，故在此选取该值为放大系数，考虑到行车工况复杂多变需设置安全冗余以及简化计算满足工程实际需要，将车体偏移统一放大，确保计算结果安全可靠。

控制点在竖直方向的偏移无法直接计算，可通过计算CD，求得OC，继而获得CG之间距离，将该部分位移叠加同侧一二系位移悬挂位移后乘以相应的放大系数μ。对于由一位侧二位侧悬挂位移不同引起的车体倾斜角度变化已由倾角传感器获得，此处不再重复考虑。计算公式如下：

(4)

式中：y1为同侧一系悬挂位移，mm；y2为同侧二系悬挂位移,mm。

当车辆中心线与轨道中心线的倾角向左时,控制点A(x,y)位移的计算原理见图8。

控制点横向偏移通过计算BD间距离间接获得，计算公式为：

x′=x-μ(x-(xcosα-ysinα)+xc)

(5)

对于控制点竖向位移，计算公式为:

y′=y+μ(xsinα-(y-ycosα)+y1+y2)

(6)

对于车下部分的动态包络线计算，横向为2D激光补偿位移，竖向为悬挂位移。在结合两个断面计算结果，选取最大轮廓为车辆动态包络线。

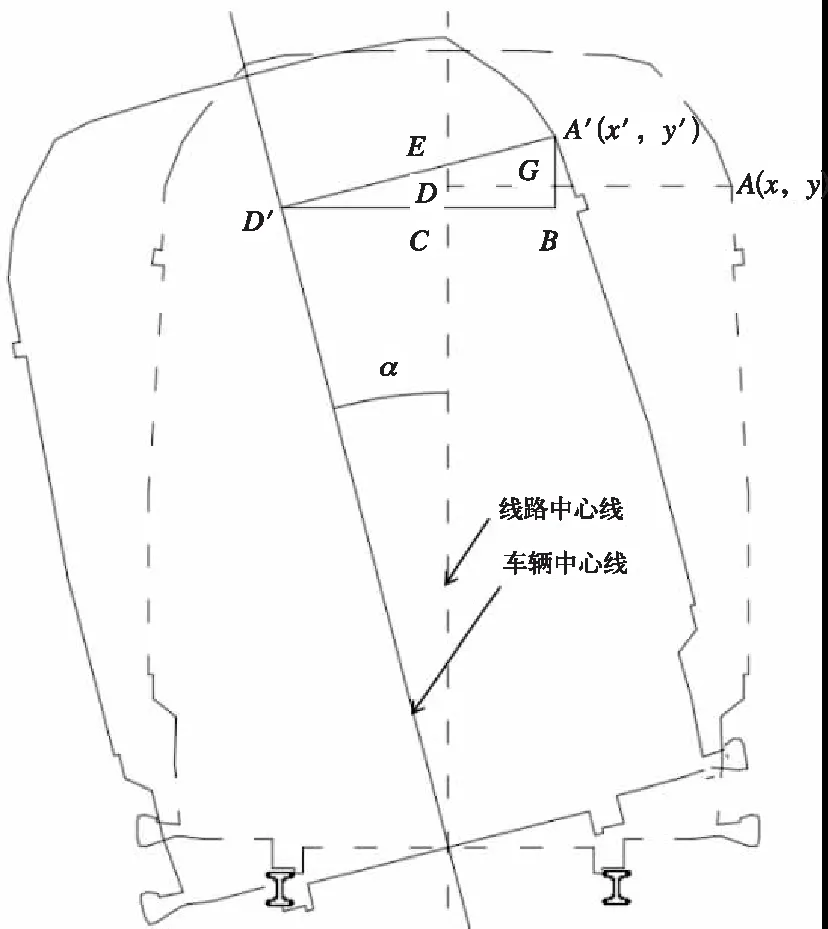
图8 倾角向左算法原理

2.3 软件实现

软件的编写采用C#语言，C#语言运算速度快，有丰富的GUI程序，适合该算法的实现，软件流程见图9。

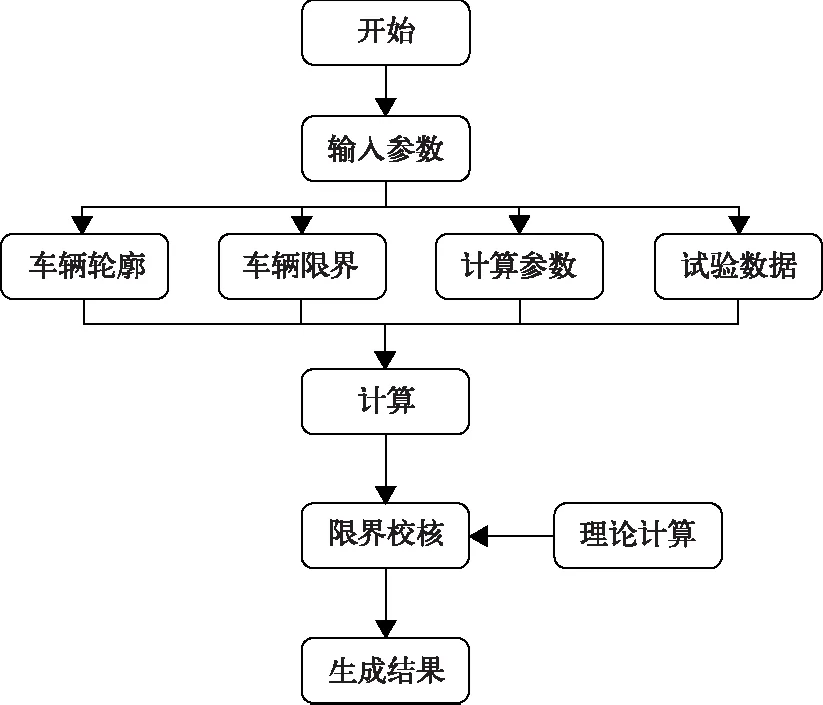
图9 软件工作流程

软件功能主要包括：导入车辆参数、试验参数、试验数据并动态显示全数据段动态包络线；生成包络线坐标文件并进行限界校核；软件的主要特点有，能够适应不同类型车辆的计算需求，可以导入不同车辆参数，有很强的通用型，软件能够实时显示车辆姿态，可视性强便于观察，可以结合理论计算结果进行校核，方便后续计算报告等的处理。软件界面见图10：

3 对比分析

选取北京地铁燕房线阎村至星城区段为分析路段，试验现场风速3.4 m/s、风压720 N/m2。对叠加算法与CJJ96地铁限界标准中算法，以及线路试验结果进行对比。该段为直线线路，且线路坡度变化较小，适合进行对比分析。

图10 软件界面

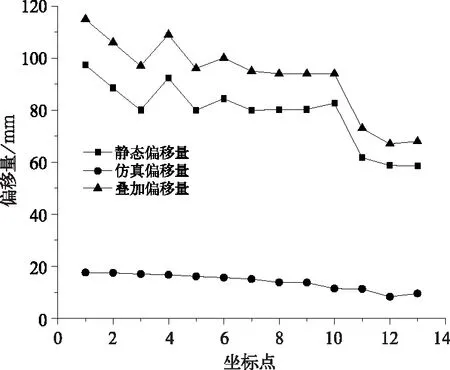
图11 横向偏移量对比

图11所示为叠加算法车体横向偏移量构成，可以看出，由安装误差等造成的静态偏移量占主导部分。随着控制点高度的下降，偏移量也呈现略微下降趋势，与实际情况相符。图12所示为仿真模型风压720 N/m2情况下，叠加算法与CJJ96标准算法对比结果，为衡量动态包络线较车辆轮廓偏移程度，定义偏移度参数δ,mm。

(7)

式中：p1i为车辆轮廓控制点；p2i为偏移后轮廓控制点；n为控制点个数。

求和项为两控制点之间L2范数。经计算CJJ96《地铁限界标准》算法偏移度为121.31 mm,叠加算法偏移度为101.14 mm，缩小约16%与预期结果较为吻合。采用叠加算法，通过动力学仿真计算，能够避免过极端工况，将行路条件、车辆参数等更加紧密的结合起来，而不是简单的线性求和。结果更加贴近车辆真实运行姿态。

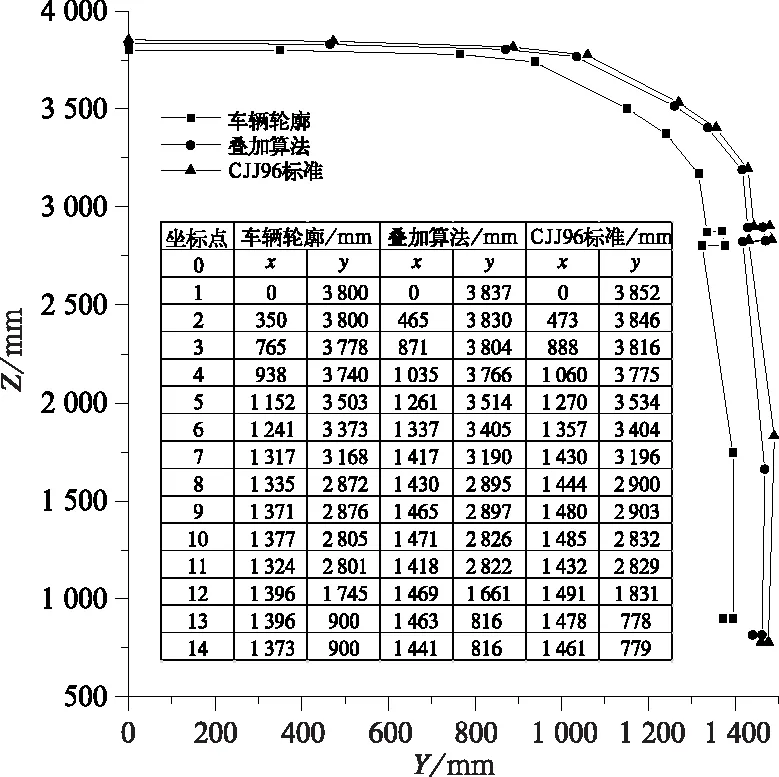
图12 叠加算法与CJJ96标准算法对比

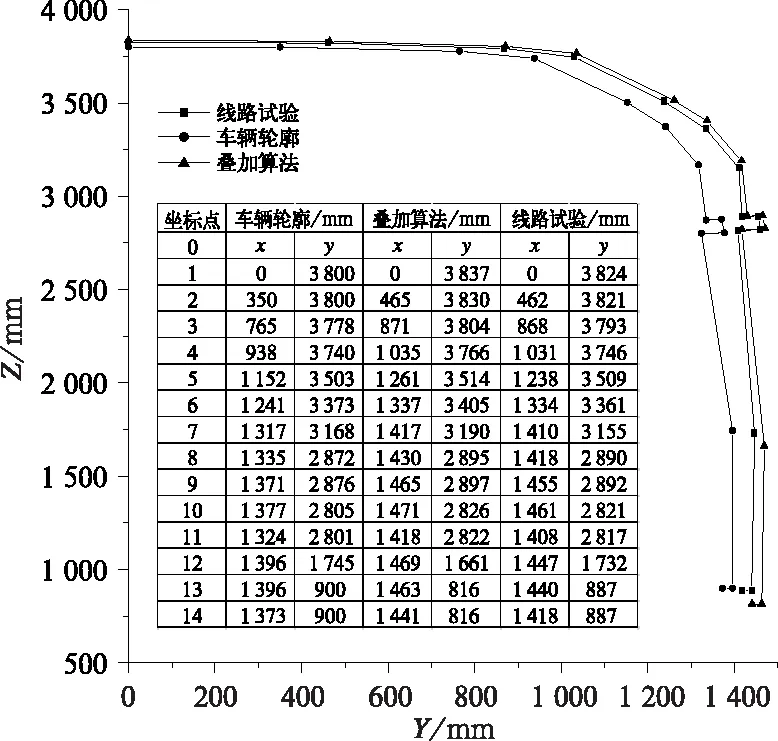
图13 线路试验与叠加算法对比

图13所示为风压720 N/m2情况下，动态包络线线路试验与叠加算法对比结果，线路试验结果偏移度为81.93 mm，缩小约19%，结合试验当天天气、风力，且线路属于新建直线线路等因素，车辆运行相对更为平稳，试验动态包络线在处于合理区间之内。

4 结 论

由对比分析可知:

(1)3种算法所得到动态包络线偏移趋势基本一致，在车肩与车辆底部有较大差别，这与车肩位置的高度、线路条件、仿真误差等都有一定关系。采用叠加算法，所得计算结果更为贴近实际测试结果，为动态包络线理论计算提供参考。

(2)采用基于位移倾角精确检测技术的动态包络线线路试验，为动态包络线的验证以及试验方法进行了初步探索，由于本身试验主要针对车体部分，下一步的研究可以增加对车下部分，以及车下部件之间位置关系的研究，以获取更加完整的动态包络线，对限界空间的精细化利用有重要意义。