团簇Fe3Cr3电子自旋与磁性分析

廖 薇，方志刚，赵振宁，李历红，秦 渝

(辽宁科技大学 化学工程学院，辽宁 鞍山 114051)

科学技术的发展促使人们认识到了非晶态合金，即一种可以将金属所具有的可变形性、韧性、导热性和导电性等特性与玻璃所具有的优良绝缘性和抗腐蚀能力等特性相结合的新型材料[1].近年来，具备独一无二的物理及化学性质的非晶态合金发展迅猛[2-5]，其中大多为铁磁合金，即一种属于软磁材料却又优于传统磁性材料的合金体系[6-8].其中过渡金属Fe对一系列铁基非晶态合金所显示出的独特优势作出了极大贡献，加之Fe具有很强的铁磁性，铁基非晶态合金的磁性无疑备受广大科研工作者的关注[9-11].目前，已有的非晶合金相关成果主要从宏观角度对其物理性质进行研究，如Liu等[12]基于铁基非晶态合金在电力变压器、电机和转换器等各种能源相关工业的广泛应用中探究出了一种从边缘玻璃成形器中获得纳米结构铁基合金的简便方法，但微观角度的理论研究报道甚少.此外，Cr作为与Fe一样的过渡金属，两者的性质在一定程度上有相似之处，而两者所形成的非晶态合金Fe-Cr亦引起了一些关注[13].鉴于此，本文结合文献[14]将非晶态合金Fe-Cr二元体系原子比例确定为3∶3，以团簇Fe3Cr3模型模拟非晶态合金，从电子自旋角度就其稳定性和对磁性贡献极大的电子自旋磁矩展开深入研究，以期为已有的非晶态合金Fe-Cr体系有关研究提供理论支撑，并为今后的相关研究提供有价值可参考的信息.

1 计算方法与构型的优化

1.1 理论模型的建立

基于拓扑学原理[15]构造出团簇Fe3Cr3以各种可能空间结构存在的理论异构体模型，主要包括平面六边形型、五棱锥型、四角双锥型以及戴帽三角双锥型.

1.2 实验计算方法

以密度泛函理论[16]为主要基础，将已设计出的团簇Fe3Cr3初始构型于启天M4390微机上的Gaussian09程序中采用B3LYP泛函以及程序内置的Lanl2dz基组(即B3LYP/Lanl2dz方法)分别进行处于单重态与三重态下的相关优化计算，计算过程中对过渡金属原子Fe和Cr均采用18-eECP双ξ从头计算基组[17]，最终选择了团簇Fe3Cr3稳定性相较于单重态构型更好的8种三重态优化构型.此外，对各优化构型的电子自旋布居数等相关计算通过Multiwfn多功能波函数分析程序[18]完成.

2 结果与讨论

2.1 团簇Fe3Cr3的三重态优化构型

经全参数优化计算后，继续对含虚频的不稳定构型进行排除，最终确定了团簇Fe3Cr3处于三重态下的8种稳定优化构型，如图1所示.其中以能量最低即最稳定的构型1(3)为基准，分别计算出余下7种构型的相对能量并按能量增长趋势对其进行编号排序，同时将具体能量值分别标于对应构型图下方.此外，编号右上角括号内数字表示自旋多重度，即代表构型所处重态条件为三重态.

在图1的8种优化构型中，所属类型最多的为戴帽三角双锥型，其次为四角双锥型，而五棱锥型有且仅有1个.就能量而言，前3种构型(1(3)～3(3))能量明显低于其余5种，而最后2种构型(7(3)和8(3))能量也明显高于其余构型，由此可将8种优化构型划分为3类： 第1类构型(1(3)～3(3))能量值小于35kJ/mol；第2类构型(4(3)～6(3))处于100～200kJ/mol；第3类构型(7(3)和8(3))大于200kJ/mol，且三者的热力学稳定性大小表现为： 第1类>第2类>第3类.说明构型1(3)最为稳定而构型8(3)最不稳定.

图1 团簇Fe3Cr3的优化构型图Fig.1 Pictures of optimized configurations of cluster Fe3Cr3

2.2 团簇Fe3Cr3的自旋布居分析

电子自旋现象又称电子的内禀运动，当中α电子自旋方向为向上而β电子自旋向下.此外，单重态构型为闭壳层，其2个自旋的空间轨道同等，基态分子的电子自旋成对，即净自旋为零；而三重态构型为开壳层，分子中含有α和β 2个自旋不配对的电子，即净自旋不为零.由此，本文中与电子自旋相关的研究仅对团簇Fe3Cr3的8种三重态构型展开.其中，自旋布居数为α布居数与β布居数的差值(自旋布居数=α布 居数-β布居数)，对其进行分析可准确具体地就原子或原子轨道所带单电子的种类及数目展开讨论，且自旋布居数为正值对应带α单电子而负值则对应带β单电子.

2.2.1 各原子的自旋布居分析

表1(第218页)为团簇Fe3Cr38种三重态优化构型基于Mulliken所得各原子的自旋布居数，其中： ΣFe与ΣCr分别为各Fe、Cr原子自旋布居数矢量和，可以体现相反自旋方向的成单电子相互抵消后剩余的单电子种类及数目；Σ|Fe|与Σ|Cr|则为绝对值之和，表示Fe原子与Cr原子的总成单电子数.

对表1数据进行分析可得，除构型5(3)的3个Fe原子自旋布居数均为正值之外所有构型的Fe原子和Cr原子自旋布居数均有正有负，说明构型5(3)中3个Fe原子的单电子均为α电子，而余下各构型的3个Fe原子和3个Cr原子均有带自旋向上的α单电子和带自旋向下的β单电子.根据表1中Σ|Fe|与Σ|Cr|数据绘制出图2所示的曲线图，由图2可知8种构型的Σ|Cr|均大于Σ|Fe|，表明Cr原子所带单电子数目多于Fe原子.此外，由图2可直接看出构型1(3)和6(3)所展现出的趋势变化最为特殊，其中构型1(3)的Σ|Fe|与Σ|Cr|相距最远而构型6(3)的Σ|Fe|与Σ|Cr|相距最近，说明构型1(3)中成单电子分布极不均匀，具体表现为多数分布于Cr原子、少数分布于Fe原子，构型6(3)中则分布极其均匀.对于较为稳定的第1类构型(1(3)～3(3))，各个Cr原子布居数绝对值均大于相应Fe原子绝对值，且Cr原子布居数多为正值而Fe原子多为负值，所以整体来看在这3种构型中α单电子主要分布于Cr原子而β单电子主要分布于Fe原子；对于稳定性居中的第2类构型(4(3)～6(3))，其所呈现出的现象与第1类构型稍有相似，各个Cr原子(除了构型6(3)的Cr3：-1.567)布居数绝对值均大于相应Fe原子绝对值，且Cr原子布居数多为负值而Fe原子多为正值，可得这3种构型中α单电子主要分布于Fe原子而β单电子则主要分布于Cr原子；对于最不稳定的第3类构型(7(3)和8(3))，可明显看出除构型7(3)的Cr3(2.848)和构型8(3)的Cr1(2.886)之外的Cr原子布居数绝对值仍大于相应Fe原子绝对值，且Cr原子中布居数为正值的和(7(3)：7.854和8(3)：7.972)大于Fe原子(7(3)：3.590和8(3)：3.609)，Cr原子中布居数为负值其绝对值亦大于Fe原子，即在这2种构型中α与β单电子均主要分布于Cr原子.

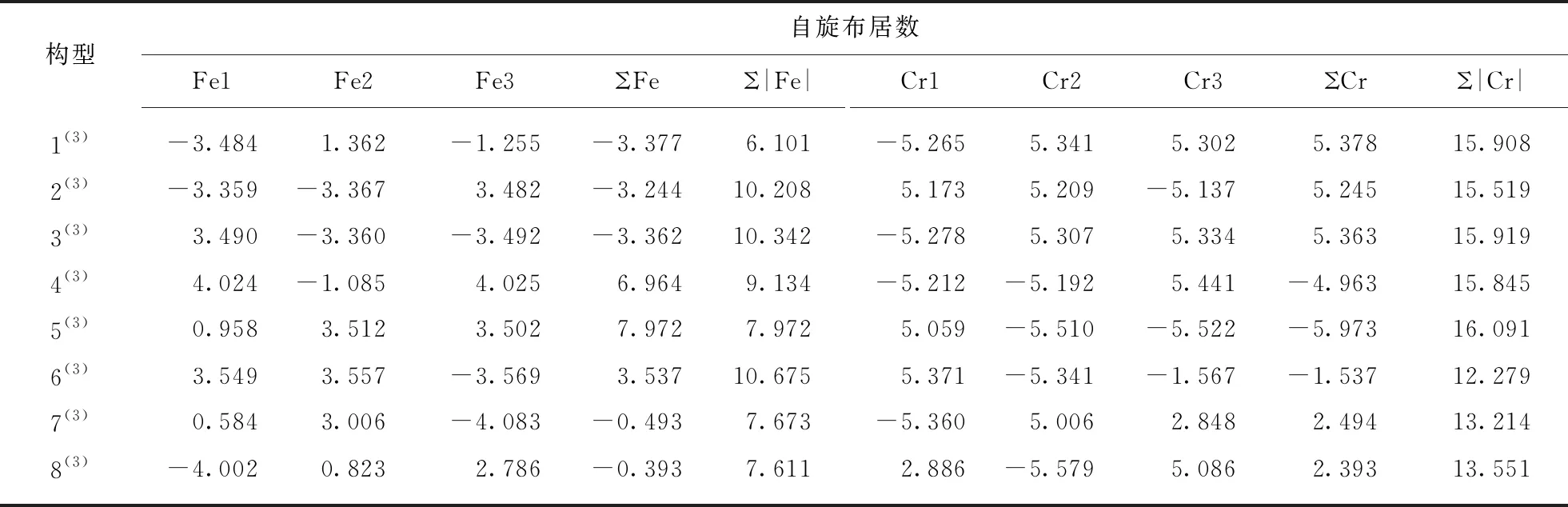
表1 团簇Fe3Cr3优化构型中各原子的Mulliken自旋布居数

图2 团簇Fe3Cr38种优化构型的Mulliken自旋布居数Σ|Fe|与Σ|Cr|曲线图Fig.2 Graph of the Mulliken spin population of Σ|Fe| and Σ|Cr| in eight optimized configurations of cluster Fe3Cr3

2.2.2 不同原子各原子轨道的自旋布居分析

团簇Fe3Cr36个原子在8种不同优化构型中所带成单电子，即为表1所示Mulliken自旋布居数，分别分布于各种角动量基函数—相应原子的s、p、d原子轨道，同时对应自旋布居数及总和的具体数据见表2.由表2中数据可直接看出，每个构型中6个原子的d轨道自旋布居数绝对值均大于s轨道和p轨道，且Cr原子的自旋布居数绝对值绝大多数相较于Fe原子更大，说明所有构型中各原子的单电子均主要分布于d轨道，且整体上Cr原子d轨道上的单电子多于Fe原子.s轨道和p轨道的自旋布居数并无绝对明确的大小关系，但大多数构型中各原子的s、p轨道自旋布居数正负同步，即带有同自旋方向的成单电子.较为特殊的是，在最稳定的第1类构型(1(3)～3(3))中，构型1(3)的Cr1原子s轨道带自旋向下的β单电子(-0.602)、p轨道带自旋向上的α单电子(0.024)；在稳定性一般的第2类构型(4(3)～6(3))中，构型4(3)Fe2原子(s： -0.152、p： 0.026)与Cr1原子(s： -0.573、p： 0.026)s、p轨道所带单电子情况同构型1(3),而稳定性较差的构型5(3)其Cr1原子(s： 0.329、p： -0.003)和Fe1原子(s： 0.043、p： -0.070)则均带相反单电子；在稳定性最差的第3类构型(7(3)和8(3))中，2个构型均有多个原子的s、p轨道带异自旋方向的成单电子.综合说明构型的热力学稳定性与α、β成单电子在相应s、p原子轨道的分布情况密切相关，即s与p轨道上的异自旋方向成单电子在一定程度上会削弱构型的稳定性.此外，8种构型中s、p轨道的异自旋方向成单电子主要分布于Cr1原子.

表2 团簇Fe3Cr3优化构型中各原子不同原子轨道的Mulliken自旋布居数

2.3 团簇Fe3Cr3的电子自旋磁矩

电子自旋磁矩是分子磁矩最主要的贡献者，其中未成对电子即成单电子自旋所产生的磁矩对分子磁矩影响最大，且自旋相反的电子的自旋磁矩可相互抵消，因此电子自旋磁矩与成单电子的分布情况以及单电子的自旋方向密切相关，具体表现为自旋向上的α单电子所产生磁矩为正，对体系磁性起促进作用；而自旋向下的β单电子所产生磁矩为负，对体系磁性起抑制作用.电子自旋磁矩通常用成单电子数(自旋布居数n)与玻尔磁子μB表示为nμB，μB在国际标准公制下的定义为

式中：e为电子电荷量；h为普朗克常数；me为电子质量，计算得出：μB=9.274×10-24J/T.

分子整体的自旋磁矩可以分解成各原子、各原子轨道的贡献.结合表1中ΣFe与ΣCr的具体数据绘制出图3所示曲线图，对图3进行分析可知，同类构型中各构型的ΣFe与ΣCr正负号完全相反，表明同类构型中各构型的Fe原子内部经相反自旋方向的成单电子相互抵消后余下的单电子自旋方向与Cr原子恰好相反，即Fe原子与Cr原子所产生的磁矩正负亦相反.如对于第1类构型中最为稳定的构型1(3)，其ΣFe为负值(-3.377)而ΣCr为正值(5.378)，则Fe原子与Cr原子产生的磁矩分别为-3.377μB和5.378μB.值得一提的是，由图3可明显看出除第2类构型(4(3)～6(3))之外余下所有优化构型的ΣCr绝对值均大于ΣFe绝对值，再综合表1中各原子的自旋布居数可知，对于团簇Fe3Cr3每一种优化构型中6个原子的自旋布居数而言，具有最大值和最小值的均为Cr原子，且由表1数据得出结论“Cr原子所带单电子数目多于Fe原子”，最终说明过渡金属Cr对构型磁矩的贡献最大从而对团簇磁性的影响也最大，同样也可以说明Cr的含量会对非晶态合金Fe-Cr体系的磁性产生极大影响.此分析结果为已有的相关研究[19-20]进行了佐证，又因前人就此方面的研究至今还停留在宏观角度的定性描述水平，而本文从微观角度清晰准确地对其作出了解释与验证.此外，文中2.2.2节对表2的分析发现团簇Fe3Cr3所有构型中各原子的单电子均主要分布于d轨道，表明d原子轨道对构型磁矩的影响最大从而导致对团簇磁性影响最大.

为便于直观地表征团簇Fe3Cr38种优化构型的s、p、d原子轨道对磁矩的贡献情况与特点，将表2各构型不同原子的原子轨道进行同类加和，最终分别得出各构型总的s、p、d轨道自旋布居数，由此绘制出图4所示柱状图并标出相应数值.由图4可直接看出，在8种优化构型中，d轨道自旋布居数均为正值并大于s轨道和p轨道，可得在每一种优化构型中d轨道都是电子自旋磁矩的主要贡献者，且均为d轨道上自旋向上的α成单电子对团簇磁性起最强促进作用.此外，s轨道在各构型自旋布居数数值均较小但正负不统一，说明s轨道对团簇电子自旋磁矩影响不大，对磁性所起作用效果也不固定.值得一提的是，对于稳定性最差的构型7(3)和8(3)，其d轨道(3.170和3.273)和p轨道(-1.014和-0.938)的自旋布居数绝对值相较于余下6种构型均更大，即表明d轨道和p轨道在这2种构型中对电子自旋磁矩即磁性的影响相较于其余构型更大.其中d轨道对构型7(3)和8(3)电子自旋磁矩的贡献分别为3.170μB和3.273μB，其α成单电子所产生磁矩对团簇磁性起最强促进作用；而p轨道分别为-1.014μB和-0.938μB，其β成单电子所产生磁矩对团簇磁性起最强抑制作用.

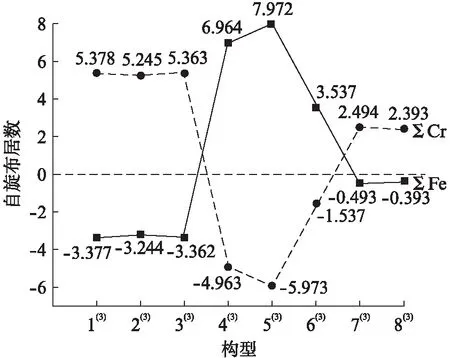
图3 团簇Fe3Cr38种优化构型的Mulliken自旋布居数ΣFe与ΣCr曲线图Fig.3 Graph of the Mulliken spin population of ΣFe and ΣCr in eight optimized configurations of cluster Fe3Cr3

图4 团簇Fe3Cr38种优化构型s、p、d轨道的Mulliken自旋布居数柱状图Fig.4 Histogram of the Mulliken spin population of s, p and d orbitals in eight optimized configurations of cluster Fe3Cr3

3 结 论

电子自旋布居不仅可以表现各原子、原子轨道的未成对电子分布情况，还可与玻尔磁子μB共同表示对体系磁性起主要作用的电子自旋磁矩.研究团簇Fe3Cr38种三重态异构体基于Mulliken所得的一系列自旋布居数发现： 所有构型中Cr原子所带单电子数目均多于Fe原子，且各原子的单电子均主要分布于d轨道，表明d轨道是电子自旋磁矩的主要贡献者，且其自旋向上的α单电子对团簇磁性起最强促进作用；同类构型中各构型的Fe原子内部经相反自旋方向的成单电子相互抵消后余下的单电子自旋方向与Cr原子恰好相反，Fe原子与Cr原子所产生的磁矩正负亦相反；大部分构型中各原子的s、p轨道带有同自旋方向的成单电子，且s与p轨道上的异自旋方向成单电子在一定程度上会削弱构型的稳定性.另外，本文从微观角度证明过渡金属Cr对构型磁矩的贡献最大从而对团簇磁性的影响也最大，继而对已有“Cr的含量多少会对非晶态合金Fe-Cr体系的磁性强弱产生极大影响”的相关宏观研究提供了理论支撑与解释.