基于全电子方法和TB-mBJ势的硫化镉多型体能带结构计算

张元珏，高尚鹏

(复旦大学 材料科学系，上海 200433)

硫化镉(CdS)是一种重要的Ⅱ-Ⅵ族半导体化合物，广泛应用于太阳能电池、光电导探测器、光致发热和光探测等领域.CdS/CdTe多晶薄膜太阳电池效率高，通过改变导电薄膜和窗口层材料，效率可达16.5%[1]，已有很多商业化的光伏电站.CdS、CdSe及其固溶体被用于可见光辐射探测[2].以TiO2为代表的传统催化剂因具有较宽带隙，导致可见光响应范围较窄，并具有光催化量子产量低等不足.CdS材料因其具有理想的导带边和价带边，较窄的禁带宽度、良好的光导电性和较高的电子亲和能等优点，适宜在可见光下用于分解水制氢而受到广泛研究.Kaveri[3]等通过浸渍法制得CdS/rGO,其对甲基橙的降解率可在120min内达到99%.Yan[4]等合成了Pt-PdS/CdS光催化剂，可见光下量子效率达到93%.

CdS的热力学稳定相是纤锌矿结构(w-CdS)[5-6]，闪锌矿结构的CdS(zb-CdS)[7-8]也很常见.在高压下，纤锌矿结构和闪锌矿结构CdS都会转变为岩盐矿结构CdS(rs-CdS)[9].人们从实验上研究了3GPa左右到更高压强(如55GPa)范围的rs-CdS的禁带宽度、光学和介电性质[10-11].

CdS的光伏、光电和光催化性能与禁带宽度密切相关.传统的基于局域密度近似(Local-Density Approximation, LDA)和广义梯度近似(General Gradient Approximate， GGA)的密度泛函理论(Density Functional Theory, DFT)在计算激发态相关性质的时候存在明显的误差.在进行半导体和绝缘体的能带计算时，密度泛函理论得到的结果和实验值相差可达50%.HubbardU修正[12]可以处理4d电子的局域强关联作用.采用杂化交换关联泛函如HSE或者多体微扰理论框架下的GW方法可以得到更准确的禁带宽度，但是计算量很大.Trans和Blaha提出改进的Becke-Johnson势(TB-mBJ)可以在相对于常规DFT-GGA计算不显著增加计算量的情况下得到和实验符合较好的禁带宽度.本文探讨了HubbardU修正[12]与TB-mBJ势[13-15]对能带结构和电子态密度的影响，并采用TB-mBJ势进行更精确的电子结构计算，分析了外加压强下rs-CdS的禁带宽度变化趋势.

1 计算方法

1.1 晶格优化

使用CASTEP[16-17]软件进行晶格优化，赝势方法选择为程序在线产生的模守恒赝势(OTFG Norm Conserving)，平面波截断能设置为1000eV.交换关联势选择为广义梯度近似中的Perdew-Burke-Ernzerhof(PBE)[18]，采用了Grimme-D2半经验的色散修正来考虑长程范德瓦尔斯作用.自洽计算的能量收敛判据选择为5.0×10-7eV/atom.倒空间网格密度划分方式为Monkhorst-Pack散点法： w-CdS为7×7×4；zb-CdS(计算中采用原胞)为7×7×7；rs-CdS(计算中采用原胞)为8×8×8.晶格优化方法选择为BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法，收敛判据为能量5.0×10-6eV/atom，最大力0.01eV/Å，最大应力0.02GPa，最大位移5.0×10-4Å.

1.2 电子能带结构和态密度分析

本文的能带结构与态密度计算均采用WIEN2k[19]软件，基于全势线性缀加平面波(Full Potential Linearized Augmented Plane Wave, FP-LAPW)方法，这是用于能带结构计算的最精准方案之一.为克服LDA与GGA交换关联势普遍低估禁带宽度的问题，本文采用了HubbardU修正和TB-mBJ势以获得更为精确的能带结构.HubbardU修正是对部分填充的过渡金属元素强局域化d(f)轨道添加一个库伦排斥项U，也称为LDA+U或GGA+U方法，本文中对Cd-d轨道设定的U值为5eV[20].TB-mBJ是近年来提出的一种meta-GGA势，除了对电子密度、电子密度的梯度的依赖之外，近似考虑了电子密度二阶导数的影响，对于s和p轨道电子计算具有更高的准确性.本文在GGA自洽计算的基础上使用TB-mBJ势进行能带结构与态密度计算，称为mBJ-GGA方法.

自洽计算时的精度主要由参数Rkmax控制，Rkmax为最小原子球半径RMT乘以最大的K矢量Kmax，本文采用的Rkmax值为7.5.自洽计算中采用PBE交换关联泛函，同时在整个布里渊区内采用1000个k点，并将分离能设置为-6.0Ry(81.634eV).收敛判据为电荷变化≤10-3eV.

2 结果与讨论

2.1 常压下稳定相w-CdS和zb-CdS的能带结构和电子态密度

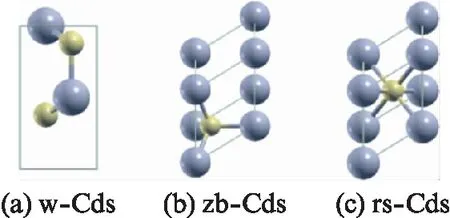
图1 硫化镉多型体晶体结构示意图Fig.1 CdS polymorphs shown as primitive cell均以原胞形式表示.灰色为镉原子，黄色为硫原子.

纤锌矿、闪锌矿与岩盐矿结构的CdS晶体结构如图1所示，它们分别隶属于P63mc(186)、F-43m(216)和Fm-3m(225)空间群.计算所得纤锌矿结构CdS的晶格常数为a=b=4.128Å,c=6.698Å和实验结果a=4.136Å,c=6.713Å[6]的差值小于0.3%，内坐标u=0.3773也和实验值0.37715[6]吻合地很好.闪锌矿结构CdS的晶格常数为a=b=c=5.825Å，和实验值5.818Å[8]非常接近；岩盐矿结构CdS的立方晶格常数为5.301Å.3种硫化镉多型体内部原子坐标如表1所示.

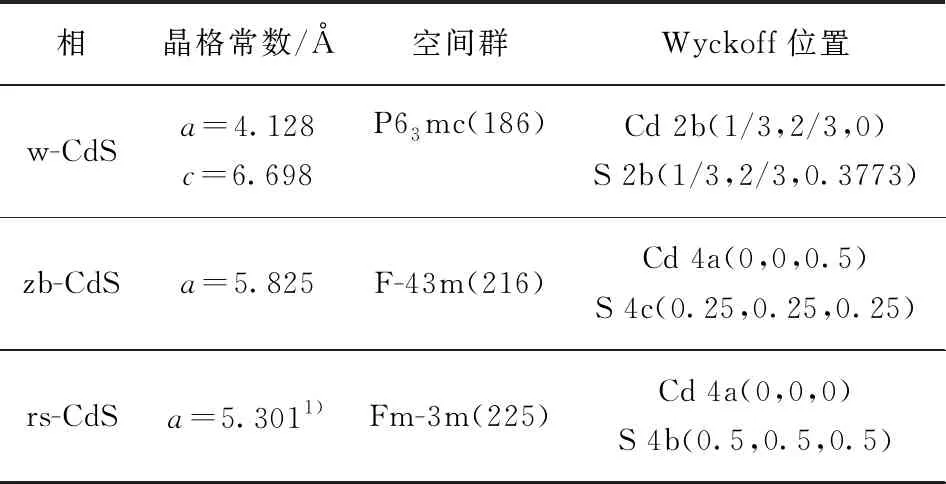
表1 CdS多型体的晶体学参数

注： 1) 5.296(5GPa)，5.223(10GPa)，5.111(20GPa)，5.027(30GPa)，4.958(40GPa)，4.900(50GPa)

对岩盐矿结构CdS施加压强后，其晶格常数随压强增大而不断减小.在0，5，10，20，30，40和50GPa压强下的晶格常数见表1.

自旋-轨道耦合(Spin-Orbit Coupling， SOC)会导致轨道能级细小分裂，影响晶体的能带结构.考虑了自旋轨道耦合效应后，不同交换关联势计算的能带结构结果如图2(见第210页)所示.在纤锌矿结构CdS中，考虑自旋轨道耦合效应后，能带结构仅有微小差别，对于价带深能级以外的能带影响可以忽略.在GGA、GGA+U和mBJ-GGA交换关联势下，考虑自旋轨道耦合影响后得到的禁带宽度差值分别为-0.01eV、-0.02eV和0.03eV，近似忽略不计.可见自旋轨道耦合效应对于纤锌矿结构CdS影响十分微小，在后文的计算中，我们将不考虑自旋轨道耦合带来的影响.分别采用3种不同交换关联势GGA、GGA+U和mBJ-GGA得到w-CdS与zb-CdS的能带结构如图3所示.从图3中可以看出，w-CdS和zb-CdS都是直接禁带半导体，价带顶(VBM)和导带底(CBM)均位于Γ点.采用DFT-GGA得到的w-CdS和zb-CdS的禁带宽度分别为1.22eV和1.14eV.由于Cd含有局域强关联作用的4d电子，HubbardU修正在一定程度上增大了禁带宽度，并对深能级的能带位置产生了影响.采用GGA+U得到的w-CdS和zb-CdS的禁带宽度分别为1.47eV和1.38eV.mBJ-GGA的方法对于禁带宽度的影响非常大，使得禁带宽度增大了1倍以上，得到的w-CdS和zb-CdS的禁带宽度分别为2.74eV和2.66eV.

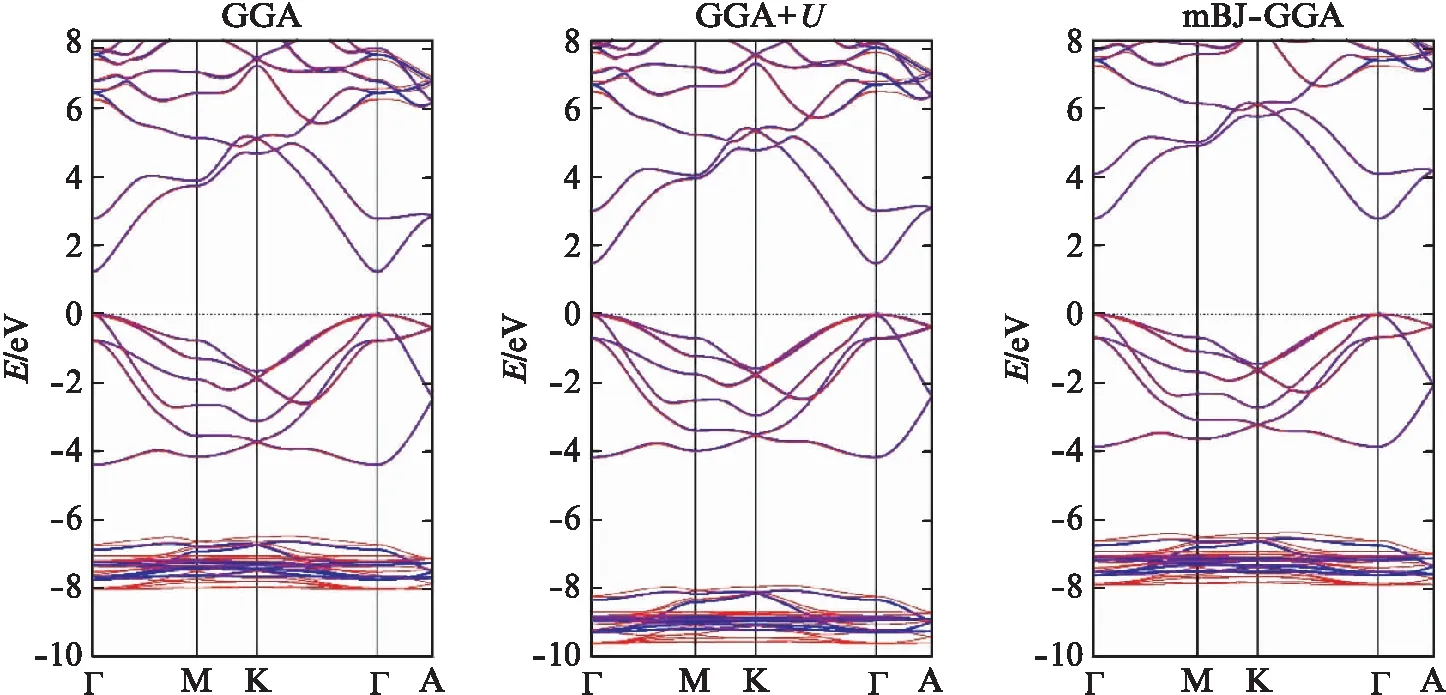
图2 自旋轨道耦合对纤锌矿结构硫化镉能带结构的影响Fig.2 The effect of SOC on the band structure of ws-Cds原始能带结构为蓝色，考虑自旋轨道耦合影响能带结构为红色.

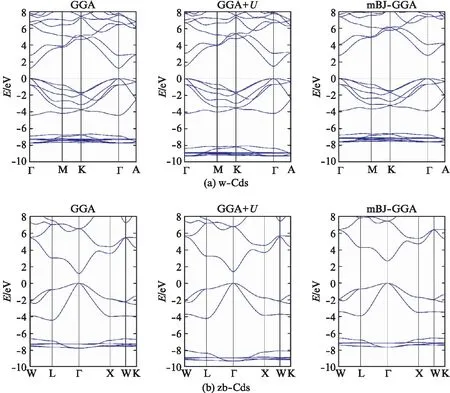
图3 分别采用GGA、GGA+U、mBJ-GGA交换关联势计算所得(a) 纤锌矿结构硫化镉能带结构和(b) 闪锌矿结构硫化镉能带结构Fig.3 The band structures of (a)w-CdS and (b)zb-CdS calculated by DFT with exchange-correlation functional approximated by GGA, GGA+U and mBJ-GGA

采用mBJ-GGA、GGA+U和GGA交换关联势得到的纤锌矿结构CdS的禁带宽度的值分别为2.74eV、1.47eV和1.22eV，得到的闪锌矿结构CdS的禁带宽度计算值分别为2.66eV、1.38eV和1.14eV.对于这2个体系，计算所得禁带宽度的大小顺序均为mBJ-GGA>GGA+U>GGA.

CdS禁带宽度的实验值集中在2.5eV左右，Soltani[21]等以硫化钠作为硫源制备的闪锌矿CdS量子点带隙实验值为2.54～2.61eV，以硫代乙酰胺作为硫源制备的纤锌矿CdS量子点带隙实验值为2.62～2.65eV.在3种交换关联势近似中，GGA与GGA+U的方法计算所得禁带宽度均远小于实验值，这一方面是由于GGA会低估体系禁带宽度的固有缺陷，另一方面是由于在处理强关联体系时，GGA没有考虑占据与非占据的d或f轨道之间的能量差，这两方面的原因导致GGA禁带宽度计算结果远小于实验值.在添加库伦参数U之后，禁带宽度有所提升，但和实验值之间仍有较大差距.mBJ-GGA交换关联势使得禁带宽度计算值与实验值相当接近，误差在10%以内，可见mBJ-GGA势对于CdS体系具有很好的修正作用，计算所得禁带宽度相较于传统GGA准确了许多，展现了mBJ交换关联势在禁带宽度计算方面的优势.GGA+U的方法依赖于经验参数U，主要对所设定轨道(Cd元素4d轨道)产生影响，对于其他轨道几乎不产生效果.mBJ-GGA的方法且对于所有原子轨道的势能均有所修正，使禁带宽度大幅度增加，落在实验值附近.mBJ-GGA的方法计算计出的纤锌矿与闪锌矿结构CdS禁带宽度与实验值吻合地很好，展现了TB-mBJ交换关联势在禁带宽度预测上的优势.后文中关于岩盐矿结构CdS的能带计算将统一采用mBJ-GGA方法.

为了更细致的分析不同交换关联势对电子态的影响，分别采用GGA、GGA+U、mBJ-GGA交换关联势得到w-CdS与zb-CdS的电子总态密度与分波态密度，如图4所示.从图4中我们可以看出，w-CdS与zb-CdS构成价带顶与导带底的组分一致，价带顶均由Cd-d、Cd-p轨道与S-p的轨道构成，导带底主要由Cd-s轨道与S-p、S-s轨道构成.HubbardU修正降低了Cd-d轨道在价带顶附近的态密度，减少了其对于价带顶的贡献；而mBJ修正降低了S-p在导带底附近的态密度，减少其对导带底的贡献.

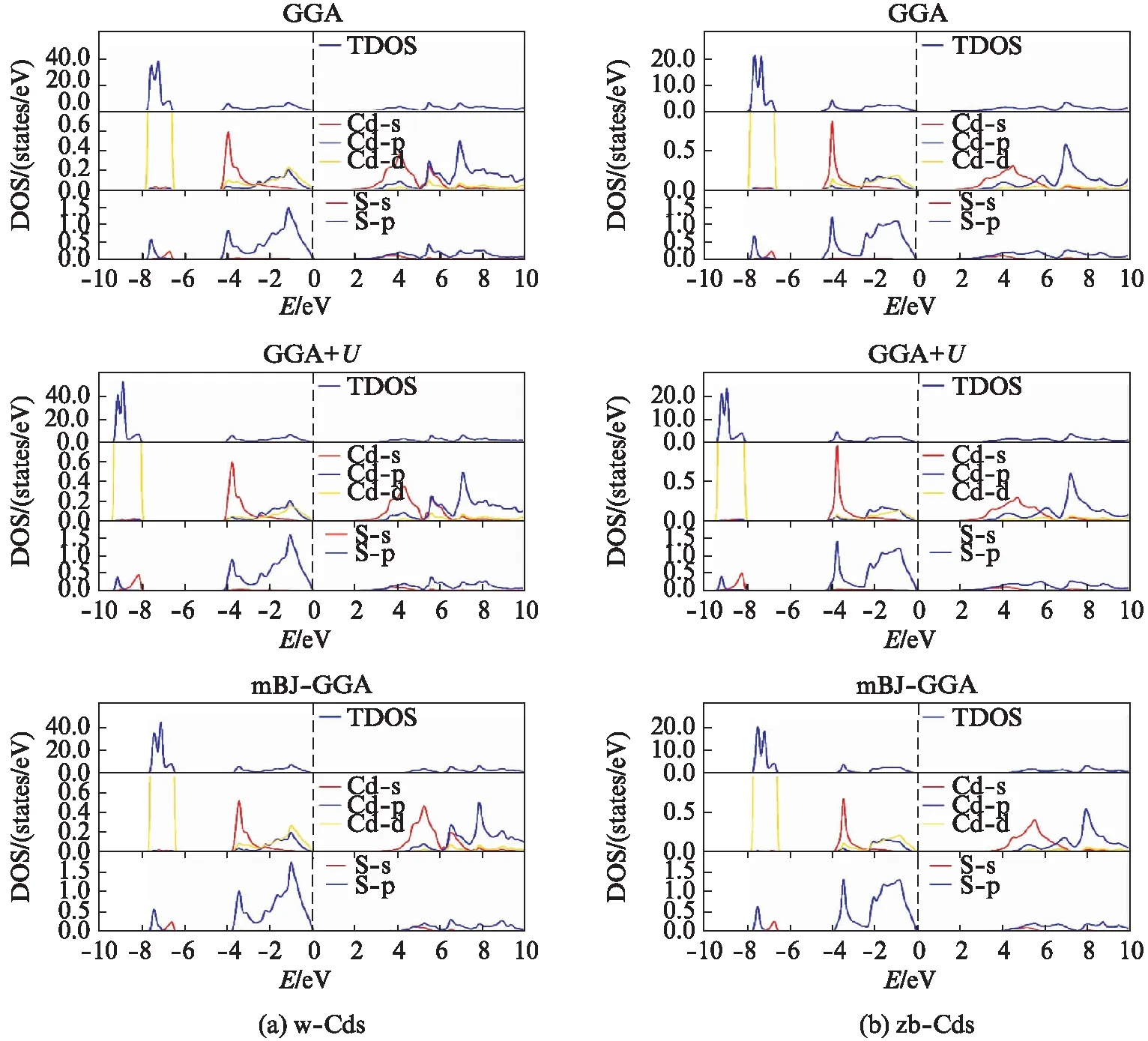
图4 分别采用GGA、GGA+U、mBJ-GGA交换关联势计算的(a) 纤锌矿结构硫化镉和(b) 闪锌矿结构硫化镉的电子总态密度与分波态密度Fig.4 The TDOS and PDOS for (a)w-CdS and (b)zb-CdS calculated using GGA, GGA+U and mBJ-GGA

从图4中可以看出，对于w-CdS与zb-CdS，总态密度在深能级处出现一个很强的峰，该峰主要由Cd-d轨道构成，展现了该轨道的强局域性，其与S-s轨道和S-p轨道都有耦合现象产生.对于2种结构硫化镉，在GGA交换关联势下，该强局域峰均分布在-6.8eV到-7.8eV范围内.纤锌矿结构硫化镉的Cd-d局域峰的更高，强度约为闪锌矿结构硫化镉的2倍.在GGA+U势下，该局域峰会向深能级处移动，分布将位于-8.0eV到-9.3eV范围内，同时峰的强度略微提升，同时接近价带顶区域的Cd-d轨道态密度有所减少.Hubbard U修正对Cd-d之外的轨道态密度未产生明显影响.在mBJ-GGA势下，各原子的s轨道与p轨道的形状与分布发生一定变化，价带态密度收缩，分布范围减小；导带则整体相对价带顶的位置向更高能量移动，使得禁带宽度大幅增加，同时S-p轨道对导带底的贡献减少，使得在该势下导带底主要由Cd-s轨道构成.

2.2 高压相rs-CdS的能带结构与禁带宽度随压强的变化

岩盐矿结构CdS在不同压强下的能带结构如图5所示，计算均采用mBJ-GGA交换关联势.从图中可以看出岩盐矿结构CdS属于间接带隙半导体，价带顶位于L点同时导带底位于X点.随着压强增大，岩盐矿结构CdS价带顶与导带底的位置并未产生移动.随着外加压强的不断增加，岩盐矿结构CdS计算所得禁带宽度持续减小，在0GPa、10GPa、20GPa、30GPa、40GPa和50GPa静水压强下的禁带宽度分别为1.53eV、1.49eV、1.42eV、1.34eV、1.26eV和1.18eV.随着压强增大，接近价带顶处能带的宽度不断增加，其范围从4.5eV扩大到6.5eV.岩盐矿结构CdS在深能级处也存在局域化区域，其能带位置随着压强增大而不断向能量更低的方向移动，同时伴随着宽度的持续增大.低压强下，该区域与接近价带顶的能带完全分离，随着压强的不断增加，价带顶和导带底在能量上逐渐靠近.

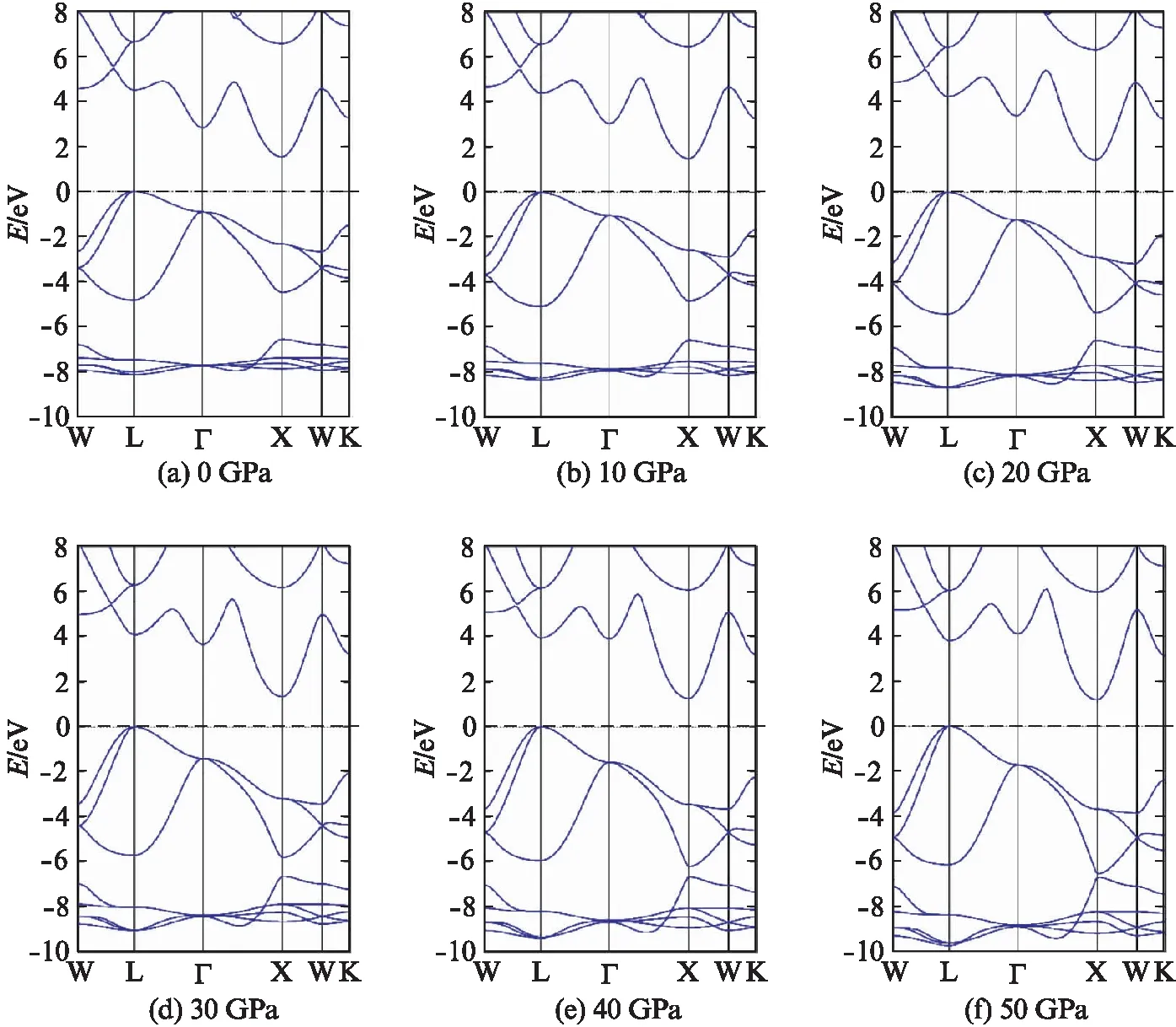
图5 采用mBJ-GGA交换关联势计算所得岩盐矿结构硫化镉分别在不同压强下的能带结构Fig.5 The band structures of rs-CdS calculated by DFT with mBJ-GGA exchange-correlation functional under different pressures

岩盐矿结构CdS的禁带宽度与晶格常数随压强变化的变化趋势如图6所示，外加压强会导致晶体的尺寸减小，即晶体的晶格常数不断缩小，岩盐矿结构CdS的晶格常数在0GPa到50GPa范围内从5.3Å逐渐减小到4.9Å.随着压强的不断增加，禁带宽度也从1.53eV逐渐减小到1.18eV.

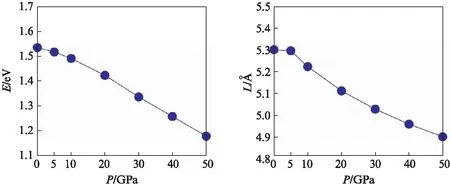
图6 岩盐矿结构硫化镉的禁带宽度与晶格常数随压强变化关系Fig.6 Dependence of the rs-CdS band gap and lattice constant on pressure

在0～30GPa范围内，禁带宽度变化的速率随着压强变大而不断增大，在20～30Gpa范围内，体系的禁带宽度改变幅度最大；在30～40GPa和40～50GPa 2个区间内，禁带宽度变化幅度相较于20～30GPa范围略微减小，且趋向于稳定.这些数据表明，通过加压可以有效减小体系的带隙[22].一般来说，对于半导体，压力越大带隙越小，这是因为高压下原子之间的距离缩小，相互作用加强，推高了费米面；而从唯相角度讲，这时候体系的能量应该升高，而因为半导体是填满的，所以只有费米面升高才能提高系统的能量.

Cervantes等[10]对岩盐矿结构CdS外加压强，测得其禁带宽度在10～55GPa范围内，随压强增大而持续减小，从约1.5eV变化到约1.2eV.其使用LDA势进行能带结构计算，在10GPa时禁带宽度降为0eV，无法与实验相互印证.本文采用GGA-mBJ势计算的能带结果，禁带宽度在10～50GPa压强范围内从1.52eV变化到1.18eV，与实验数据吻合程度高，表明TB-mBJ势下的能带结构计算可以很好的预测不同外加压强下的rs-CdS禁带宽度变化趋势.

3 结 论

本文通过采用不同交换关联势的密度泛函理论计算对纤锌矿结构CdS和闪锌矿结构CdS的结构、能带结构和电子态密度进行了系统研究.结果表明： GGA交换关联势都会低估2种不同CdS构型的禁带宽度，加入HubbardU修正后的GGA+U势对禁带宽度的预测有所改善，但仍与实验值存在较大差距.采用mBJ-GGA势计算的纤锌矿与闪锌矿结构CdS的禁带宽度值分别为2.74eV和2.66eV，与实验值(约2.5eV)吻合较好，展现了TB-mBJ势在能带计算上的优势.继而采用GGA-mBJ势研究岩盐矿结构CdS禁带宽度随外加压强变化的趋势，计算结果表明： 岩盐矿结构CdS的禁带宽度随压强增大而减小.当压强从0GPa逐渐上升到50GPa的过程中，岩盐矿结构CdS保持价带顶在L点导带底在X点的间接带隙特征，其禁带宽度从1.53eV逐渐减小到1.18eV，与高压下岩盐矿结构CdS光学吸收实验值相互印证.