n维无向超环面网的(l,2n)控制数

谢 歆，项诗景

(1.黄山学院 数学与统计学院，安徽 黄山 245041； 2.华侨大学 数学科学学院，福建 泉州 362021)

本文采用文献[1]中有关图论的术语和记号，用图表示网络.图的直径和连通度被广泛应用到图论中，可靠性和有效性是设计互连网络的重要参数.网络中从点x到点y的距离是指从x到y最短路的边数，图G的直径是任何两顶点间距离的最大数，连通度k(G)是指使得连通图G不连通所需去掉的最少顶点数.

n维无向超环面网C(d1,d2,…,dn)，顶点集为({(x1,x2,…,xn)|0≤xi≤di-1，i=1,2,…,n}.顶点(x1,x2,…,xn)相邻于2n个顶点(x1±1,x2,…,xn),(x1,x2±1,…,xn),… ,(x1,x2,…,xn±1)，这里±为模di(1≤i≤n)同余.n维无向超环面网C(d1,d2,…,dn)具有2n正则和点可迁的性质，连通度为2n，被广泛应用到网络理论中[2-4].

为了刻画实时平行系统网络传输延迟的可靠性，Flandrin等[5]，Hsu等[6]分别定义了图的m宽直径.设图G为m连通图，顶点x到顶点y的宽度为m的距离dm(G;x,y)是指最小数d使得G中存在m条内点不交且长度不超过d的(x,y)路.图G的m宽直径dm(G)是指G中任何顶点x,y宽度为m的距离dm(G;x,y)的最大值.

在m连通图中，Li等[7]定义了参数(l,m)控制数，在某种程度上(l,m)控制数比宽直径更能精确地刻画网络的可靠性.对于m连通图G和给定正整数l, 如果对于G的任一顶点x(不在S中)都存在m条内点不交且长度不超过l的(S,x)路，则称顶点集G的非空真子集S为G的(l,m)控制集.用Sl,m(G)表示G的所有(l,m)控制集集合，定义参数γl,m(G)=min{|S||S∈Sl,m(G)}为G的(l,m)控制数.

(l,m)控制数不仅推广了通常意义下的图的控制数，并且很好地度量了容错网络中的资源共享问题.一个重要而又实际问题是怎么选取(l,m)控制集S使得S中顶点数尽可能少.因此(l,m)控制数和图的其他重要参数例如(l,m)独立数[8]结合起来，能更精确地分析实时平行系统网络的可靠性和有效性的容错性.

由于确定图的(1,1)控制数是NPC(NP-Completeness)问题[9]，因此确定图的(l,m)控制数也是NPC问题.这样对于特殊的正整数l和m，确定特定网络的(l,m)控制数[10-16]显得更有意义.

1 预备知识

→…

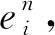
这里±为模dj同余，j=i1,i2,…,ir.

引理1[17]如果n≥2，di≥3(i=1,2,…,n)，则

引理2[17]如果n≥3，di≥3(i=1,2,…,n)，则

d2n(C(d1,d2,…,dn))=dG(C(d1,d2,…,dn))+1.

2 主要结果

引理3设G是n维无向超环面网C(d1,d2,…,dn)，S={o,u}是G的顶点子集，其中：o=(0,0,…,0)，u=(e1,e2,…,en)，这里n≥4，di≥5(i=1,2,…,n).对于任意顶点x∈V(G)-S，一定存在2n条内点不交且每条长度至多为

的S到x的路.

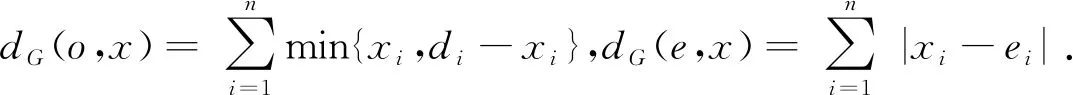
情形1顶点x的坐标都不为0.

子情形1.1顶点x的坐标xi不等于ei(i=1,2,…,n).

构造如下2n条内点不交的路，其中n条起点为o且每条长度为dG(o,x)的路P2t(1≤t≤n)，另外n条起点为u且每条长度为dG(e,x)的路P2t-1(1≤t≤n)，即

±为模dj同余(j=1,2,…,n).

子情形1.2顶点x有坐标xi值为ei(1≤i≤n).

不失一般性，设x=(x1,x2,…,xn-s,en-s+1,en-s+2,…,en)，这里0≤s≤n-1,xi≠0或ei(i=1,2,…,n-s).首先由子情形1.1可以构造n条从顶点o到顶点x的路P2t(1≤t≤n).

接着构造如下n条路，其中s条路P2t-1(n-s+1≤t≤n)起点为o，n-s条路P2t-1(1≤t≤n-s)起点为u，即

易知2n条路内点不交且长度不超过

情形2顶点x有坐标为0.

子情形2.1顶点x的坐标xi都不等于ei(i=1,2,…,n).

由点可迁性，类似于子情形1.2，可以构造2n条内点不交的路，其中n-s条路P2t(1≤t≤n-s)起点为o且每条长度为dG(o,x)，n条路P2t-1(1≤t≤n)起点为u且每条长度至多为dG(e,x)，另外s条路P2t(n-s+1≤t≤n)起点为u且每条长度至多为dG(e,x)+e′t-et.

子情形2.2顶点x有坐标xi等于ei，1≤i≤n.

不失一般性，设

x=(x1,x2，…,xn-s1-s2,en-s1-s2+1,en-s1-s2+2，…,en-s2,0,0，…,0)，

其中： 0≤s1≤n-1，xi≠0或ei(i=1,2,…,n-s1-s2).可得

类似地，容易构造2n条内点不交的路，其中n-s2条路P2t(1≤t≤n-s)起点为o且每条长度至多为dG(o,x),s1条路P2t-1(n-s1-s2+1≤t≤n-s2)起点为o且每条长度至多为dG(o,x)+e′t-et，n-s1条路P2t-1(1≤t≤n-s1-s2或n-s2+1≤t≤n)起点为o且每条长度至多为dG(e,x)，s2条路P2t(n-s2+1≤t≤n)起点为u且每条长度至多为dG(e,x)+e′t-et.

子情形1.1s=n-1.构造2n条从顶点o到顶点x且每条长度至多为dG(o,x)+6的路，即

(1)

(2)

(3)

子情形1.2s=n-2.构造2n条从顶点o到顶点x且每条长度至多为dG(o,x)+4的路，即

(4)

(5)

(6)

(7)

子情形3.2s=n-2.

如果e1-1≤min{x1,d1-x1}≤e1，且e2-1≤min{x2,d2-x2}≤e2，构造2n-2条像(4)～(7)的路，剩下2条路P3，P4如下：

路P3，P4长度至多为

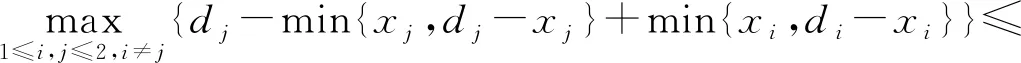
子情形4.1s=n-1.类似于子情形 3.1.

情形1顶点x的坐标都不为0.

情形2顶点x有坐标为0.

子情形2.1顶点x至少有n-2个坐标为0.

由引理4可证.

子情形2.2顶点x至多有n-3个坐标为0.

不失一般性，设x=(x1,x2，…,xn-s,0,0，…,0)，其中： 1≤s≤n-3，0

构造2n条从顶点o到顶点x内点不交且每条长度至多为dG(o,x)+2的路：

定理1证毕.

3 结论和思考