地表粗糙度及植被盖度对坡面流曼宁阻力系数的影响

杨坪坪，李 瑞※，盘礼东，王云琦，黄 凯，张琳卿

（1.贵州师范大学喀斯特研究院，贵阳550001；2.国家喀斯特石漠化防治工程技术研究中心，贵阳550001；3.北京林业大学水土保持学院重庆三峡库区森林生态系统教育部野外科学观测研究站，北京100083；4.北京林业大学水土保持学院重庆缙云山三峡库区森林生态系统国家定位观测研究站，北京100083）

0 引 言

水力侵蚀是中国主要的土壤侵蚀之一，坡面流搬运土壤颗粒致使土地生产力下降及淤积河流产生洪涝灾害。目前，各种影响因子对坡面流作用的机理机制是重要的研究课题[1-5]。坡面流阻力综合反映地表物质对坡面流的阻滞能力，是坡面水动力学研究中的重要参数。按照Abrahams等[6]对坡面流阻力的分类，由土壤颗粒摩擦引起的坡面流阻力称之为颗粒阻力，与地表粗糙度相关；坡面流绕流较大形状物质而引起的能量损失称之为形态阻力，绕流植被产生的植被阻力是形态阻力的一种，与植被盖度、排列形式等有关。研究不同地表粗糙度和植被盖度交互作用下坡面流阻力的变化规律，对坡面土壤侵蚀机理的研究和防治水土流失具有重要的意义。

以达西阻力系数量化坡面流阻力，目前的研究结果表明颗粒阻力与粗糙度呈正比而与雷诺数Re呈反比[7-9]；植被阻力与盖度呈正比[1,10-13]，而与Re的关系却尚未达成共识，既有研究表明两者间呈反比[1,10]，又有两者间呈正比[11-12]，甚至还有学者认为两者之间关系与植被的类型有关[13-14]，且存在临界盖度致使两者关系相异[15]。当地表颗粒与植被共同影响时，坡面综合阻力的计算也出现了争议，早先普遍认为各种阻力引起的综合阻力由单项阻力线性叠加[6,10,16-19]。然而近来的研究却表明这种计算方式并不适合于坡面流阻力的计算之中，因为坡面流水深浅薄，各个阻力单元之间互相影响，不能简单的线性叠加计算，现已有试验证明颗粒阻力、形态阻力和降雨阻力之间不能线性叠加估计坡面流综合阻力[20-23]。

以曼宁阻力系数量化坡面流阻力，研究者研究了草被盖度与曼宁阻力系数间关系，结果表明草被盖度越高，曼宁阻力系数越大[24-26]。王俊杰等[27]研究了刚性植被覆盖下的曼宁阻力系数规律，结果表明盖度较高时曼宁阻力系数随水深、雷诺数的增加而增加，当盖度较低时呈现了相反结果，曼宁阻力系数与水深、雷诺数负相关。唐洪武等[28]研究了深水明渠水流中含刚性植物河道的曼宁阻力系数的变化，探讨了等效水力半径、等效曼宁阻力系数等的关系，并理论推导了综合阻力与颗粒阻力和植被阻力的关系，但其前提假设是床面和植被产生的剪切力是线性叠加的。杨帆等[29]将曼宁阻力系数分为了等效盖度、等效水力半径及拖拽力系数，并计算了几项的贡献率，在其计算过程之中仍然假定阻力线性叠加。总体而言，以曼宁阻力系数来研究坡面流阻力的报道较少，对颗粒阻力和植被阻力共同影响下的规律仍未有清晰的认识。此外，当植被阻力和颗粒阻力共同对坡面流作用时，在综合阻力计算中应验证线性叠加原理的适用性。

本文通过模拟的方法，模拟地表粗糙度及植被盖度在变流量下对曼宁阻力系数的影响。首先，针对用水深计算水力半径不准确的问题[28-29]，本文采用唐洪武等[28]提出的等效水力半径，进而计算等效曼宁阻力系数。随后基于阻力线性叠加的假设计算出颗粒等效曼宁阻力与植被等效曼宁阻力，对比分析两者在坡面流中的变化规律与明渠流中的变化规律，从而验证线性叠加原理是否准确，最后通过多元回归的方法提出模型模拟粗糙度、植被影响下的等效曼宁阻力系数变化规律。

1 试验与方法

1.1 试验设计与方法

本模拟试验于重庆缙云山国家森林生态站进行，试验为人工模拟冲刷试验。如图1所示，冲刷水槽长5.2 m，宽0.4 m，高0.1 m，钢制。本次试验设计坡度为5°，5°坡以上耕作要采取水土保持措施，作为临界坡度，研究该坡度下的水动力学特性具有重要意义。此外，其为野外常见缓坡坡度[30-31]，且是室内控制试验常用坡度[12,16,27,32-33]。试验水槽包括给水、稳流、试验段、尾流等部分。试验水槽前端2 m为稳流段，在水流出口放置整流栅栏以让出流的水顺直流动，中间2 m为试验段，最后1 m为尾流段。流量由阀门及压力表共同控制，流量的标定用体积法，试验共设置9组单宽流量q，分别为0.212×10-3，0.290×10-3，0.314×10-3，0.357×10-3，0.385×10-3，0.412×10-3，0.456×10-3，0.505×10-3，0.557×10-3m3/（s·m），在本试验流量冲刷下，计算得到平均水深在1 cm范围内。

本试验共设计16种坡面条件进行冲刷。在整个水槽底面铺上不同目数的水砂纸模拟不同地表粗糙度，铺设的水砂纸有40，80，120目3种，以及一组不铺设水砂纸的光滑槽底。按照床面粗糙度ks的表示方法，粗糙度ks分别为0.12，0.18，0.38 mm，光滑槽底仍具有一定的粗糙度，为0.009[22-23]。用硬质PVC圆管模拟植被的茎干，圆管高于水面，铺设于试验段，目的是通过稳流段后充分发展且稳定的水流与圆管作用。将硬质圆管投影在水槽上的面积与试验段面积之比作为植被的盖度Cr。试验采用不同的管径，其直径D分别为2，2.5和3.5 cm，以及1组不铺设模拟植被，因而可以达到不同的盖度，对应的盖度Cr分别为4.0%，6.6%，12.2%及0，该方法通过不同管径差异导致绕流阻力不同，从而研究盖度对坡面流的影响[10,12]。植被排列的方式为行状排列（图1）。横向排列5株，间距8 cm，纵向共10排，每排之间间距10 cm。不同工况条件放置时圆管中心保持一致以避免排列方式的不同所带来的误差。水砂纸、PVC管与水槽的连接用玻璃胶，用刀片刮平PVC管表面。裸坡的ks=0.009和Cr=0，即没有布设任何措施的工况，在此种条件下，只有水槽壁面对水流产生影响。

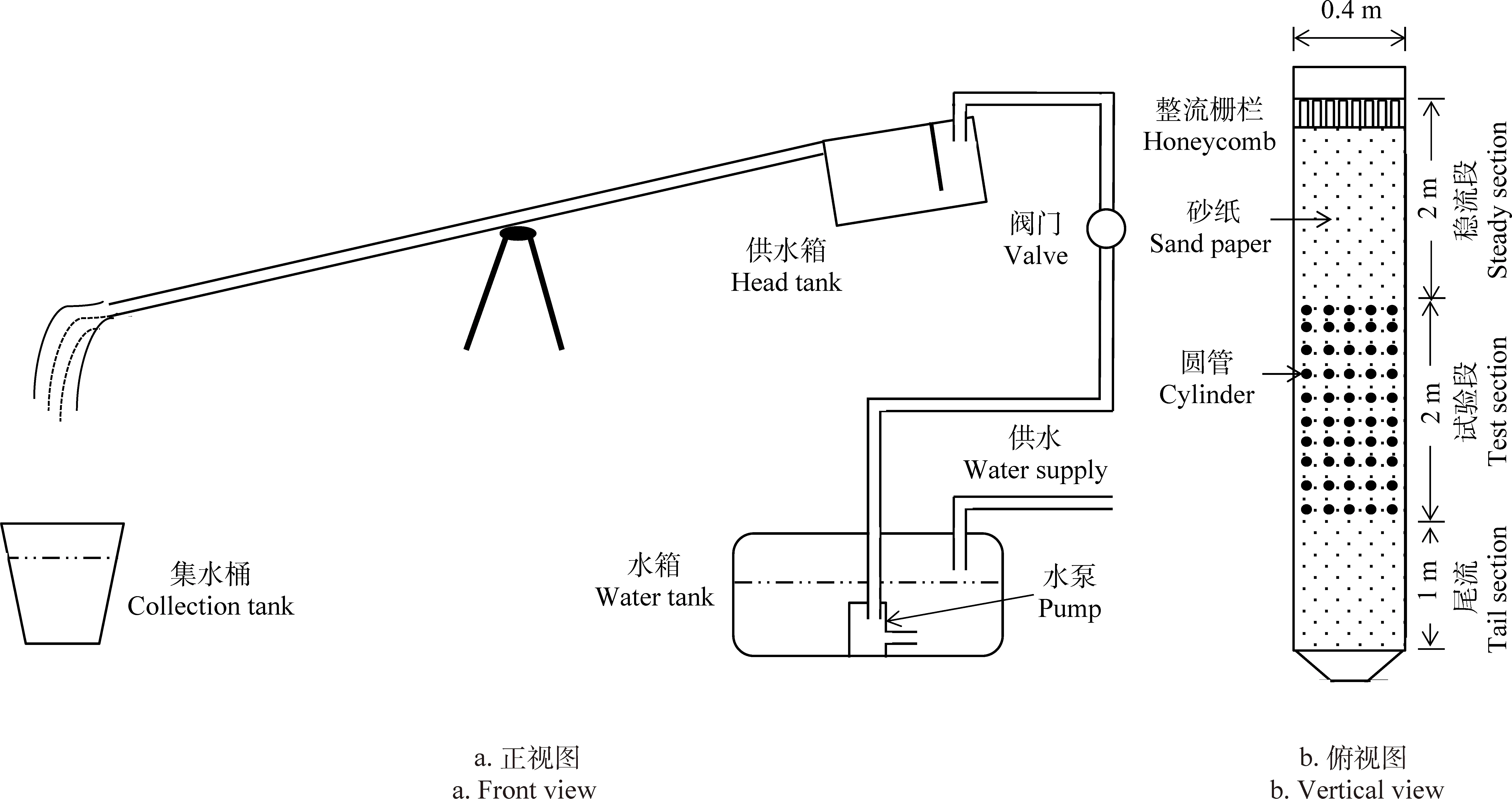
图1 试验装置示意图Fig.1 Schematic of experimental set-up

试验主要测量的数据包括流速、流量、水温，进而可以计算出曼宁阻力系数。流速的测量采用染色剂示踪法测流坡面流流速，染料使用高锰酸钾。在前人的研究之中，染色法测量坡面流流速最佳的距离为2 m[34]。在本试验中，待水流稳定后在距离试验段前0.5 m处滴入高锰酸钾，当染色剂的前端通过试验段时按下秒表，离开试验段时结束计时，通过的距离为2 m。以此来计算坡面流在试验段的流速，测量次数为10次，取平均作为平均流速。但染色剂测量的流速是表面最大流速，需乘以修正系数。该系数与试验条件密切相关，Li等[35]的研究结果表明流态为层流时流速修正系数为0.67，过渡流时为0.7，紊流时为0.8，本试验的断面平均流速u等于实测表面最大流速乘以该工况下流态对应的流速修正系数。本次试验共在9组流量、4组盖度和4组粗糙度下冲刷，因此共进行冲刷9×4×4=144场次。

1.2 参数计算

水深计算式为：

式中h为水深，m；q为单宽流量，m3/（s·m）；Cr为植被盖度，%；u为断面平均流速，m/s。水力半径是与水流接触面积相关的参数，当坡面上具有植被时，水力半径采用传统的计算方式具有偏差，等效水力半径考虑了水流与水槽壁面的接触面以及水流与植被的接触面，而传统水力半径则只考虑水流与水槽壁面的接触面[28-39]，因此采用等效水力半径Re。根据唐洪武等[28]的研究，涉水植物的等效水力半径的计算式为：

式中Re为等效水力半径，m；α为与植被盖度相关的参数，α=1-Cr；B为水槽宽度，B=0.4 m。

利用等效水力半径计算的曼宁阻力系数为等效曼宁阻力系数，其计算式为：

式中ne为综合等效曼宁阻力系数，J为水力能坡，针对坡面流，水深浅薄，本试验条件下的水深在毫米量级，沿程水位的变化范围较小，因此J可以用水槽坡度近似替代[1,5,9-16]，J=sinθ，θ为坡度。

粘性底层厚度的计算为

式中δ0为黏性底层厚度，m；ν运动黏滞系数，m2/s；u*为摩阻流速，m/s，计算为

其中g为重力加速度，9.8 m/s2。

1.3 植被阻力计算

基于唐洪武等[28]提出床面和植被对水流产生的阻力可线性叠加的思路，在本试验条件下，由于水深浅薄，水槽两侧边壁对水流产生的阻力可忽略不计，只有水槽床面及植被对水流产生作用力τ，得出如下公式：

式中τeb为水槽床面产生的阻力，为颗粒阻力；τev为植被产生的阻力，为植被阻力。

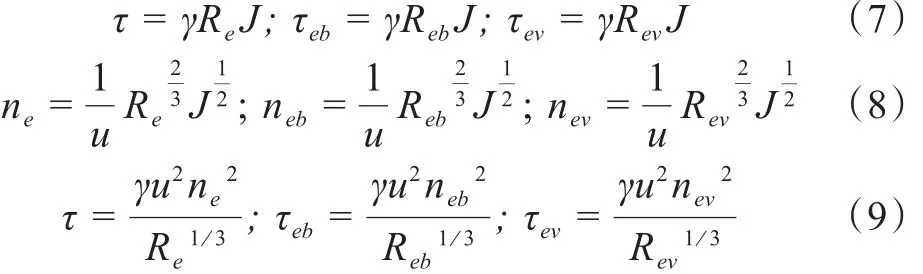
式中γ为水的重度，kg/m3；ne为综合等效曼宁阻力系数；neb和nev分别为床面和植被产生的等效曼宁阻力系数；Reb和Rev分别为床面和植被对应的等效水力半径，因边壁产生的影响不计，实际上床面和植被对应的过流断面和湿周一致，因此Re=Reb=Rev。所以由式（9）联立得到：

1.4 阻力线性叠加验证思路

当坡面没有模拟植被时，通过式（3）能够求出相应流量下ne值，此工况下仅有床面对水流产生阻力，即为地表粗糙度产生的等效曼宁阻力系数neb。当坡面上有模拟植被时，由式（3）计算出坡面ne值，再根据相应流量下地表粗糙度的neb值，由式（10）计算出nev值。对于非淹没植被，James等[36]和唐洪武等[28]的研究表明与水深h之间呈线性增加。若本文计算的nev值与h之间线性增加，表明颗粒阻力和植被阻力可线性叠加的前提假设正确，线性叠加原理可应用于坡面流阻力计算之中。而当nev值与h之间非线性增加，表明植被阻力受到其它因素影响，从而改变了变化趋势，表明阻力可线性叠加的前提假设错误，线性叠加原理不适用于坡面流阻力计算之中。产生不适用的原因是产生了附加阻力[20-23]，其计算将在2.2节中详细介绍。

2 结果与分析

2.1 综合等效曼宁糙率系数

等效曼宁阻力系数充分考虑了水流与植被的作用，使用了等效水力半径代替水力半径进行计算。研究表明当水流中有植被时，ne能更加精确的表示地表物质对水流的综合阻滞作用[28]。综合等效曼宁阻力系数ne表征床面粗糙颗粒与模拟植被共同作用下对坡面流的阻滞状况。图2所示为本文试验工况下ne随着单宽流量q的变化关系。图2a表明，粗糙度越大则ne越大。此外，随着流量的增加，ne减小，且逐渐趋于稳定。可以预见，当水深足够大时（在本文中，流量与水深间呈正相关），ne是一常数，这与在深水不含植物的明渠水流中，ne是与边壁粗糙度相关的常数相一致[28]。而在坡面流中，ne与q间呈负相关，其原因是水深浅薄，通过式（4）计算的黏性底层厚度的变化范围为0.16～0.25 mm，表明地表粗糙物质高于黏性底层，与水流核心区相互作用，而随着流量的增加，水深增加，黏性底层的厚度也逐渐增加，粗糙物质与水流核心区作用区域越来越小，则阻力越来越小；而当黏性底层高于粗糙物质高度时，则此时阻力会保持稳定不变。

由图2b，2c和2d表明当坡面存在植被时，ne却与q之间呈现正相关关系。王俊杰等[27]研究曼宁阻力系数和雷诺数Re之间的关系时，认为当Cr大于4.6%时，曼宁阻力系数随着Re增加而增加。张宽地等[15]同样在研究达西阻力系数与Re关系的时候发现，当Cr大于1.4%时，两者间由负相关转戾为正相关。原因是当Cr小于临界值时，粗糙度对坡面流的影响占优势，表现出综合阻力与Re负相关。而当Cr大于临界值时，植被阻力占优势（植被阻力与流量间正相关，因为随着流量的增加，水深增加，导致水流与植被间的接触面积变大，则植被对水流的拖拽力越大，阻力增加），表现出综合阻力与Re之间正相关。在本文条件下，当坡面具有植被时，ne和Re之间呈现出了正相关关系，是因为本文设计的最小盖度（4.0%）超过了临界盖度的值。为探究ne与ks和Cr之间的关系，将图2中每一条曲线平均，得到图3所示结果，表明随着ks和Cr的增加，ne增加。但是通过显著性检验，具有植被的坡面平均ne差异并不显著，但与没有植被的平均ne差异显著。

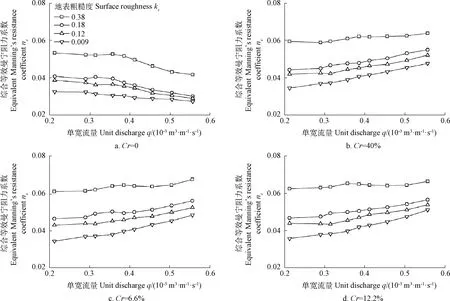
图2 综合等效曼宁阻力系数ne与单宽流量q关系Fig.2 Relationships between equivalent Manning’s resistance coefficient neand unit discharge q

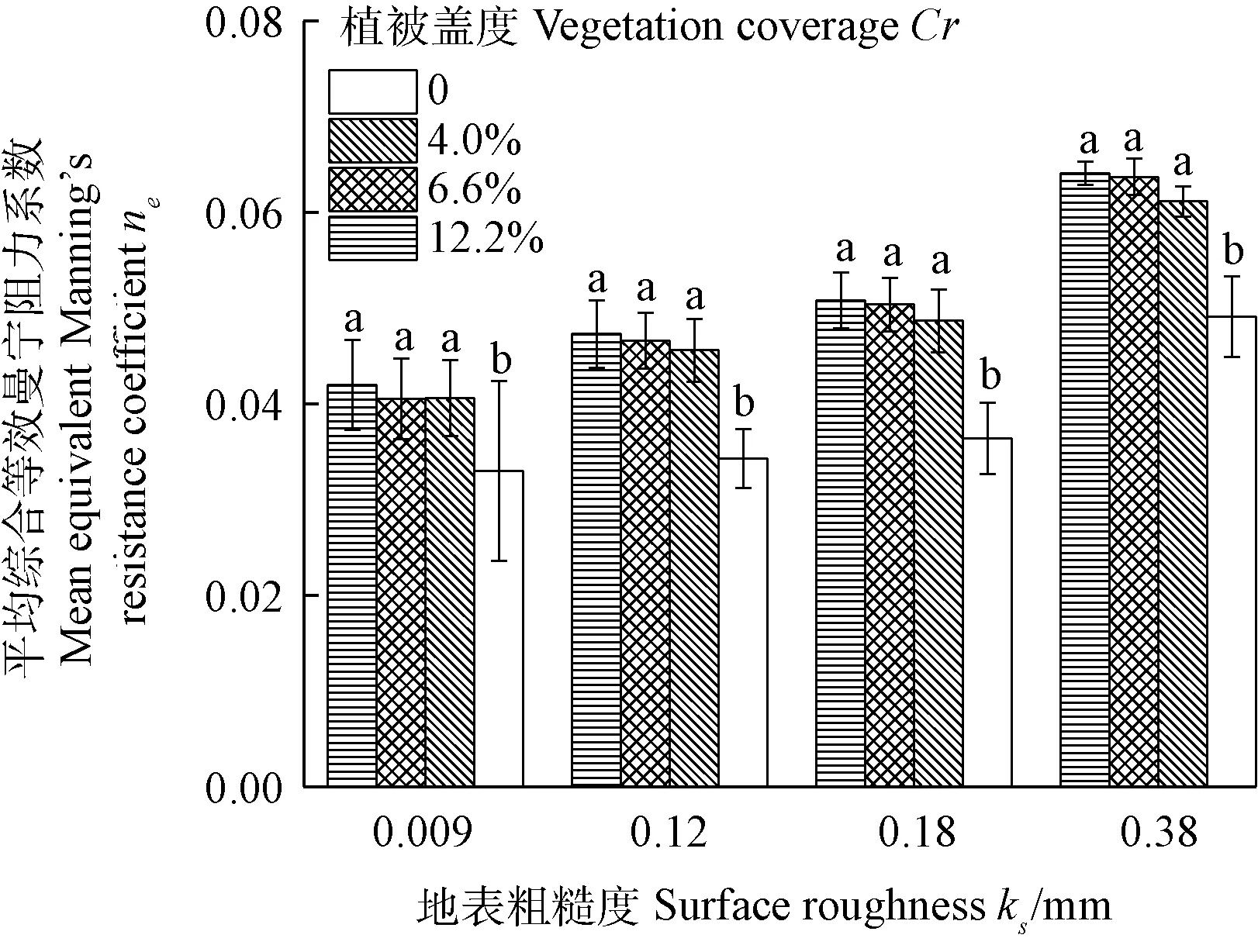
图3 平均综合等效曼宁阻力系数ne与地表粗糙度ks关系Fig.3 Relationships between mean equivalent Manning’s resistance coefficient neand surface roughness ks

2.2 颗粒等效阻力系数和植被等效阻力系数

如图4绘制了neb和nev随h之间的变化关系。图中水深不一致是与流速相关，相同流量下流速小则水深大。床面越粗糙，植被盖度越大，导致流速越小，水深则越大。图4a所示由床面粗糙引起neb随着h的增加而减小，随后逐渐趋于稳定，两者间变化趋势与前人研究结果一致[28]。图4b，4c，4d所示为由植被引起的植被等效曼宁阻力系数nev随h之间的关系，是相应工况扣除颗粒效曼宁阻力系数neb后的结果。nev与水深呈正相关，是因为随着水深增加，水流与植被之间的接触面积变大，拖拽力变大，导致nev增加。对于同一盖度条件下的nev，对水流的影响应当一致。因此在水深较大时，图4b，4c，4d所示的四条曲线之间逐渐靠拢，之间的差异越来越小。此外，根据图4的结果可以进一步的解释图2中ne随着h由先呈负相关转戾为正相关，neb和nev随着h分别呈现出负相关和正相关，当neb呈现出优势时，ne随着h呈负相关；当nev呈现优势时，ne随着h呈正相关。该结论与王俊杰等[16,28]一致。

值得注意的是，当水深较小时，不同下垫面条件引起的阻力差异较大，并非随着水深线性增加，且随着地表粗糙度的增加数据点与直线的偏离变大。James等[36]和唐洪武等[28]的研究证明nev随着h呈线性增加[28,36]。当水深较大时，本文的nev随着h呈线性增加，而当水深较小时，nev偏离直线，nev相对较大。本试验在有植被的坡面上都产生了该现象，因误差产生偏离的可能性较小。该现象表明将植被和粗糙度产生的阻力线性叠加的前提假设错误，因为如果该方法适用，则计算出的nev不论水深的大小都应随着h呈线性增加。通过对达西阻力系数的研究，Li[20]、Raws[21]和Yang等[22-23]认为采用将各个阻力子项线性叠加的方式不适用于坡面流总阻力的计算之中，因为水深浅薄，各个阻力之间并非是单独作用于坡面流，其相互之间影响，不是线性叠加的关系。从前人的研究结果推测，本试验在水深较小时nev较大，是因为产生了附加阻力。在利用式（10）计算nev时，由式（6）假定了综合阻力是由植被和床面的粗糙度产生阻力线性相加得到，并没有考虑两者会相互作用从而产生附加阻力。因此，其结果就是附加阻力产生的影响会被归入植被阻力之中，从而较大的估计了植被阻力。产生附加阻力的原因是，植被对坡面流作用的区域是在植被周围，地表粗糙度对坡面流整个区域进行影响，两者有重合作用的区域，位于植被周围。植被周围产生的涡旋与地表粗糙颗粒相互作用，会加剧流体微团的碰撞，从而能量损失较大，表现出阻力较大。当水深浅薄时，该作用尤其明显；当水深足够大时，一者粘性底层高于粗糙颗粒，则粗糙颗粒作用于水流的区域变小，导致重合作用的区域变小，二者重合区域相对于整个水深而言占比小，所以最终表现出附加阻力微弱可忽略，nev随水深线性增加。

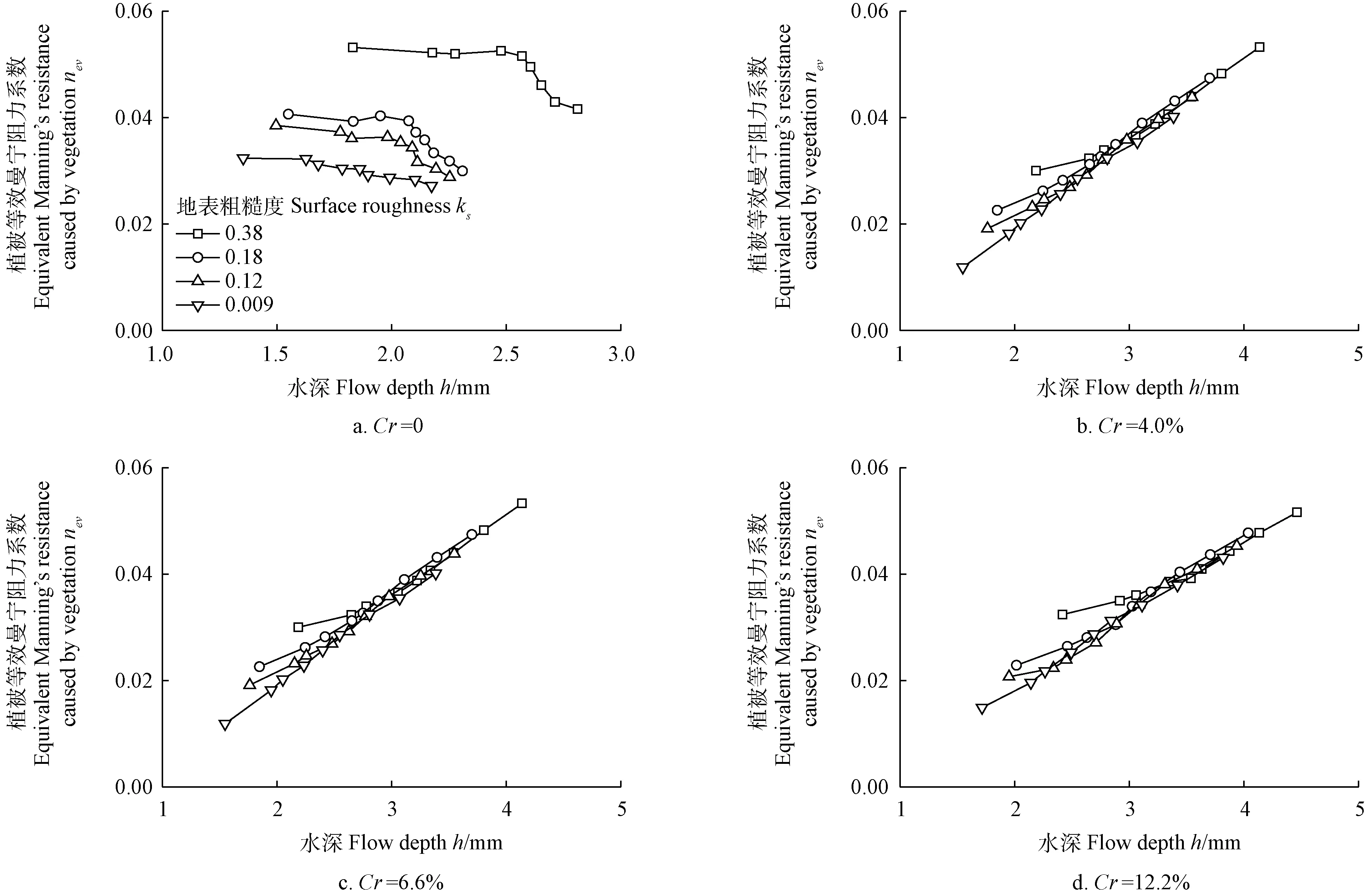
图4 颗粒等效曼宁阻力系数neb和植被等效曼宁阻力系数nev与水深h关系Fig.4 Relationships between equivalent Manning’s resistances caused by surface roughness neband cased by vegetation nevand flow depth h

为计算附加等效曼宁阻力系数na值，首先需要计算出理论nev值，在上述的讨论中表明当坡面中不存在na值时，nev随着h的增加呈线性增加。将图4b，4c，4d中曲线的最后3个点线性拟合，R2＞0.98，线性关系显著表明此时受植被阻力作用显著，而受附加阻力影响微弱，本文假定拟合的线性方程就是该条件下的nev理论计算式，随后根据h值能够计算得到较小水深下的nev理论值，将nev理论值与该水深下实际测量到的nev值相减即可得到na。如图5所示为该方法计算得到的附加阻力na随着h的变化关系，由图中可以看到，na在水深较小时其值较大，而随着水深的增加，na逐渐减小并趋于0。将图5中每条曲线平均，得到图6所示结果，ks对na影响显著，随着地表粗糙度越大，na越大；虽然当ks为0.009和0.18时，较小Cr时na值较大，但是Cr对na的总体趋势表现出Cr越大，na越大。

图5 附加曼宁阻力系数na随水深h变化关系Fig.5 Relationships between equivalent Manning’s resistance coefficient caused by additional resistancenaand flow depthh

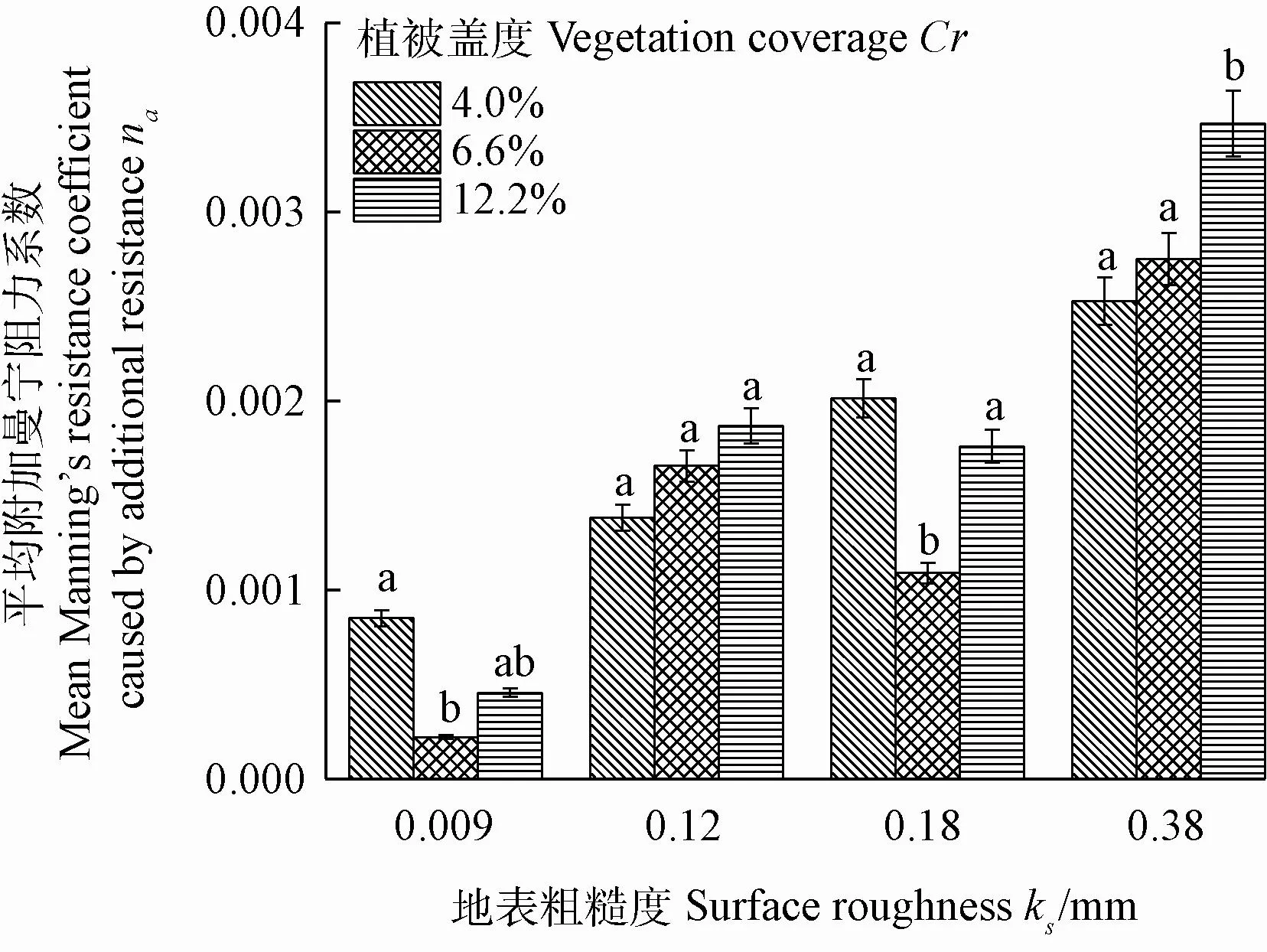
图6 平均附加曼宁阻力系数na与地表粗糙度ks关系Fig.6 Relationships between mean Manning’s resistance coefficient caused by additional resistance naand surface roughness ks

2.3 阻力计算

从前述的分析可知对于坡面薄层水流将阻力分项线性叠加并不适用，因附加阻力的存在致使nev项不随水深线性增加，需加入na对其进行修正，式（11）为修正结果。将na与nev并列的原因是，本文计算na的方法是通过唐洪武等[28]推导的理论式计算出nev，发现nev与水深的关系并非线性增加，加入na修正nev，使得修正后的nev与水深线性增加。

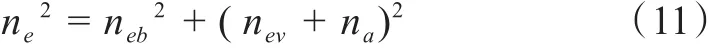
进一步的分析每一子项，neb=f(ks，h)，nev=f(Cr，h)，na=f(ks，Cr，h)，列出多项式：

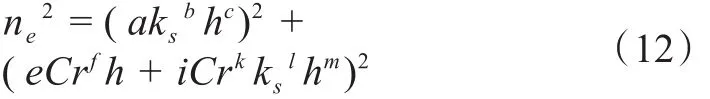
式中a、b、c、e、f、i、j、k、l、m为参数，将试验数据代入，通过多元回归分析求得参数值，从而得到以下关系：

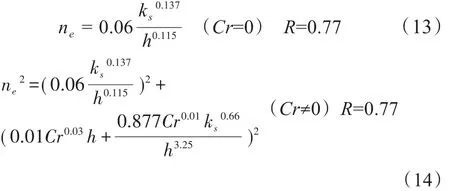
图7为ne的实测值与使用式（13）和式（14）的模拟值，当坡面存在植被时的拟合效果较好。进一步分析式（14），得到各曼宁阻力系数子项的回归方程，结果如表1所示。neb与h呈负相关而与ks呈正相关；nev与h线性正相关，与Cr呈正相关；na与h负相关，而与Cr和ks呈正相关。符合上述讨论的关系。此外，从表1的关系式中指数可知，在neb中粗糙度的贡献大于水深；在nev中，Cr的影响较小，主要为水深的影响；而对于na，水深对其影响最大，粗糙度次之，盖度对其影响最小，同时符合前文所分析的水深是产生附加阻力的重要因素。

为分析nev、neb及na对综合阻力系数的贡献值，通过剔除式（14）中相关项后所得的模拟值与实际值相比较，得出相关系数R值，比较R从而得到该项对总阻力的贡献值。当式（14）剔除nev、neb及na项后R值从0.98分别降到了0.77，0.90和0.97，结果表明对综合阻力影响的排序为：植被阻力＞颗粒阻力＞附加阻力。附加阻力的影响最为微弱，只有在水深较小的时候作用较为明显。

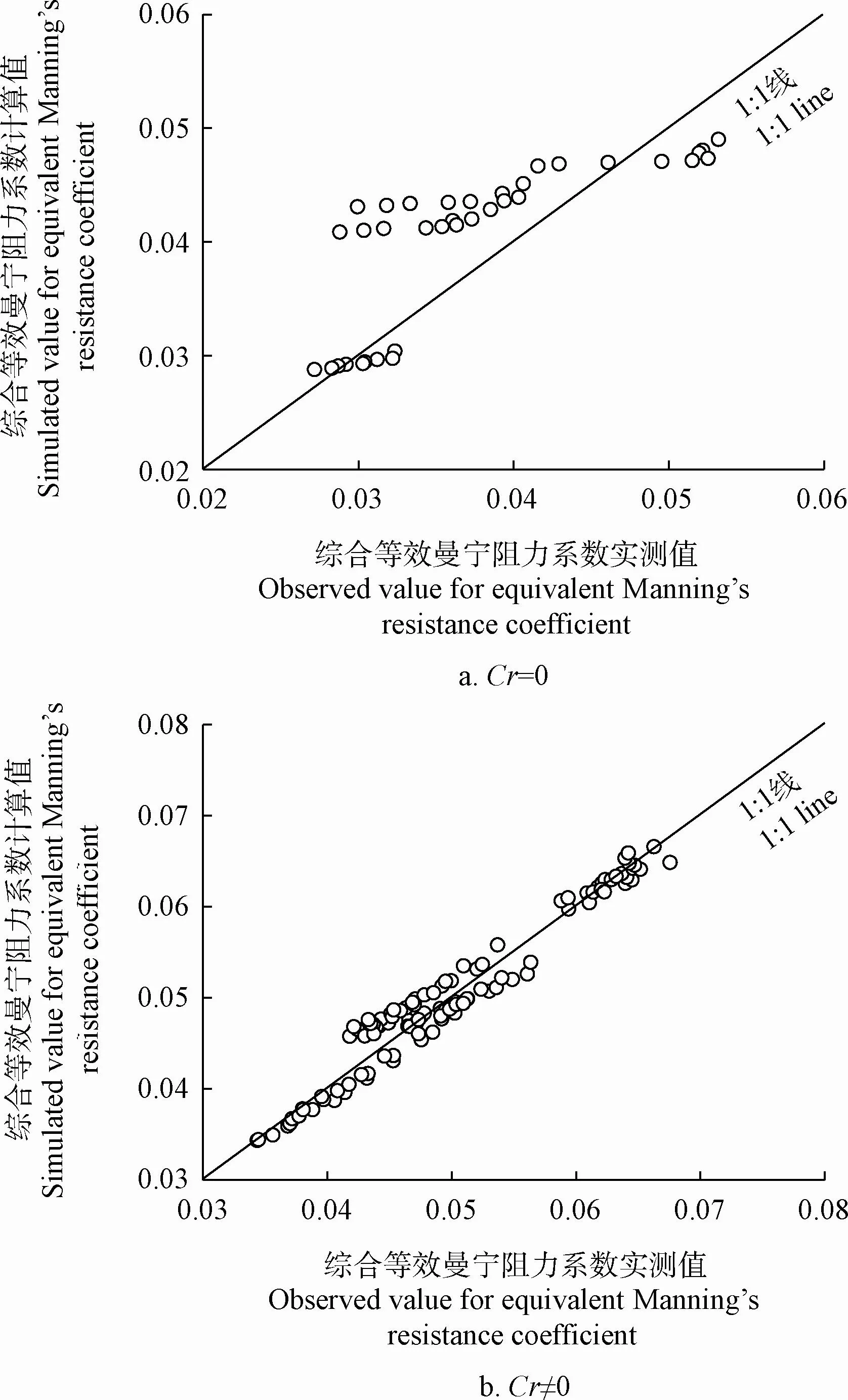
图7 坡面流综合等效曼宁阻力系数实测值与计算值比较Fig.7 Comparison between observed and simulated value for equivalent Manning’s resistance coefficient

表1 各阻力项多元回归分析结果Table 1 Results of multiple regressions for each resistant component

3 结 论

本文通过人工模拟定床冲刷试验，研究了5°缓坡条件下，4种地表粗糙度、4种盖度和9种流量冲刷下的坡面流曼宁阻力系数特征，以等效水力半径计算出坡面等效曼宁阻力系数，探讨了坡面综合等效曼宁阻力系数的变化规律，并研究了植被等效曼宁阻力系数和颗粒等效曼宁阻力系数与坡面流综合等效曼宁阻力系数的关系，结果表明：

1）综合等效曼宁阻力系数在坡面没有模拟植被时，随着流量的增加而减少；在坡面有植被时，随着流量的增加而增加。此外，综合等效曼宁阻力系数与地表粗糙度、植被盖度呈正比。

2）颗粒等效曼宁阻力系数与水深呈负相关，与粗糙度呈正相关。基于植被和粗糙度产生的阻力线性叠加假设，计算出的植被等效曼宁阻力系数与水深较不呈线性增加关系，而植被等效曼宁阻力系数应随水深线性增加，表明阻力线性叠加在坡面流中不适用。在水深较小时产生了附加阻力从而使植被等效曼宁阻力系数随水深非线性增加。随后通过加入附加等效曼宁阻力系数修正，使得修正后的植被等效曼宁阻力系数随水深线性增加。得到的附加等效曼宁阻力系数在水深较小时，其值较大，而水深较大时，趋于0。附加等效曼宁阻力系数与粗糙度、盖度正相关，而与水深负相关。

3）通过线性回归分析得到了坡面综合等效曼宁阻力系数的计算式，模拟效果较好（相关系数R=0.98）。随后进一步得到颗粒等效曼宁阻力系数、植被等效曼宁阻力系数与附加等效曼宁阻力系数的计算式，并分析得出对坡面总阻力影响最大的是植被等效曼宁阻力系数，影响最小的附加等效曼宁阻力系数。