悬索桥成桥线形求解方法比较

2020-05-18官快

广东交通职业技术学院学报 2020年1期

官快

（广东省交通规划设计研究院股份有限公司，广东广州510507）

随着国民经济的发展，基础设施的建设需求越来越大，大跨度桥梁对于跨越大江大河以及高山峡谷有自身独特的优势。大型悬索桥近年来在我国建设数量越来越多，桥梁跨径也越来越大。悬索桥的受力特点不同于其他结构形式的桥梁[1]，悬索桥在结构基本参数确定的情况下成桥状态是确定的，难以在施工过程中调整结构的最终形态，因此设计时通过计算得出相应的成桥状态显得尤为重要。

对于悬索桥成桥的线形计算，现大多采用有限变形理论有限元法[2-3]，此类方法在工程设计中有固定的计算流程，但是其计算过程比较繁琐，而且随着桥梁跨度的不断加大，结构计算的工作量也将急剧增加，此类方法计算工作量会随着计算精度的提高而成倍增加。因此如何快速获得悬索桥的成桥线形是设计中需要着重思考的问题。

本文采用分段悬链线理论[4]结合Excel软件二次开发[5]编制计算小程序，采用Excel内置计算公式快速计算出悬索桥成桥线形，同时对比采用有限元方法计算悬索桥成桥线形。分析结果证明了本文方法的可靠性和高效性，本计算方法对悬索桥成桥线形的计算以及悬索桥的设计具有一定参考和借鉴价值。

1 悬链线线形理论分析

1.1 悬索桥主缆悬链线受力分析

从受力的单索结构中取出一段微元进行受力分析[7]，通过静力平衡条件推导可得：

式中：X代表主缆节点到索起始端的水平距离；z为主缆节点到索端连线的竖向距离；H为主缆拉力的水平分力；q为沿索长均布的主缆自重荷载；c为主缆两索端点高差；l为主缆两索端点水平距离。

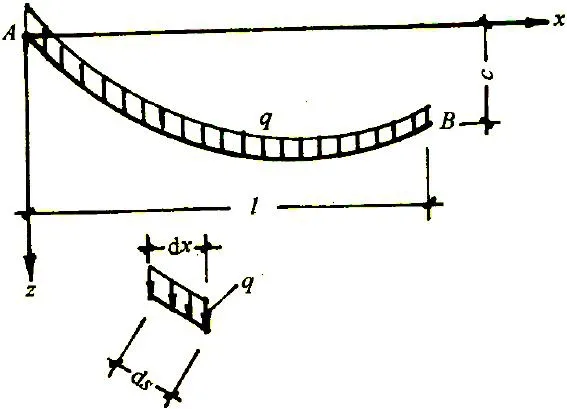
图1 悬链线受力图

1.2 悬索桥分段悬链线理论

假设吊索产生的集中力将主缆分为n段，则悬索桥主缆线形的n段满足如下的平衡及变形相容条件[4]：

b.跨中节点通过指定点；

c.各局部坐标原点处满足力平衡条件，即：

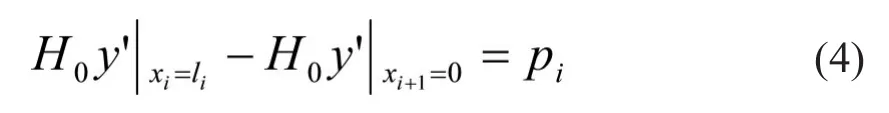
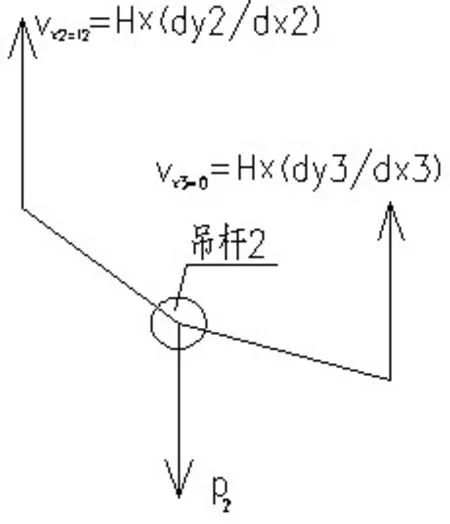
图2 吊点2局部受力平衡图

根据以上条件即可建立迭代计算过程：①根据给定的设计条件（矢跨比及跨度），按照假定抛物线线形计算可得主缆索力水平分力初始值，见式（8）。②根据加劲梁材料、断面以及桥面铺装等设计信息计算加劲梁上均布荷载值，将吊索模拟为竖向支座支撑，主梁模拟为多跨连续梁，将计算出的每处支座竖向反力作为吊杆初始索力，由加劲梁重量及主缆重量初步计算左支座处竖向力P0，由此可得：

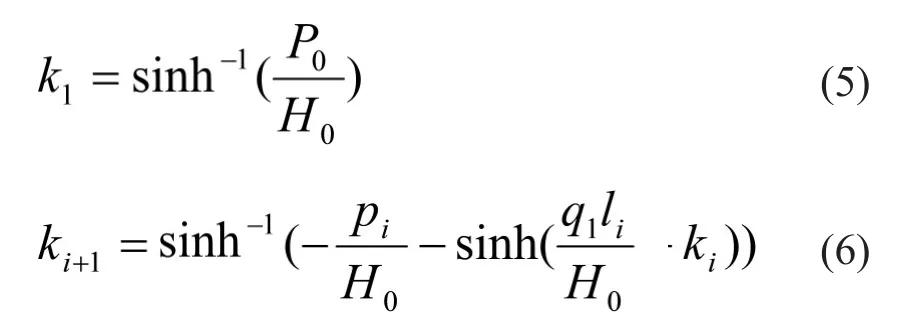
③根据各段悬链线的初始k值及悬链线公式可求出各段悬链线两端点位置高差：

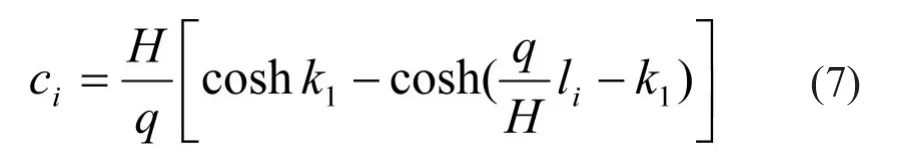
将各段悬链线两点高差进行求和，其值应该为设计值c，由于初始索力和竖向力为初步拟定值，计算出的与值有偏差。对于塔顶高程相同的悬索桥而言c=0，借助Excel的规划求解功能，为保证计算结果的精度，设定两个数值作为约束条件：首先，跨度一半的悬链线的累加竖向位移值cb（成桥线形时应为悬索桥主缆矢高f）；其次，整跨悬索桥累加竖向位移值cq（对于塔顶高程相同的悬索桥，成桥线形时其数值应为0）。根据上述约束条件可设置半跨及整垮竖向位移累加值平方和做为目标函数，将可变单元设置为水平力H0以及左端支座竖向力P0，并进行规划求解，由此求出的结果即为悬索桥的最终成桥时结构特征值。④以上所求结果为分段悬链线主缆节点坐标的解析解[6]，坐标原点为每段悬链线的左端点位置，还应在此结果上进行坐标转化，方法如下：a.每段悬链线都有相应的k值，根据每段悬链线相对于左侧端点的距离可求出悬链线局部坐标系下的竖向位移yi（相对于左端点的相对高差）；b.求解相对第一段悬链线左端点的竖向位移。这个步骤包含两种节点：一种为吊杆位置处的节点，即为每段悬链线的终点（同时也是下一段悬链线的起点，下一段悬链线的竖向位置都是在这个竖向位移的基础上累加局部坐标系下的竖向位移yi）；另一种为非吊索节点竖向位移。

首先，将需要求解的x向坐标转化为局部坐标系下的坐标，如图3。第一步确定悬链线非吊点节点m局部坐标系横坐标xm。使用vb进行Excel二次开发，采用do while语句寻找所有的吊点坐标。当发现吊点节点n的横坐标比非吊点节点m横坐标大，则节点m的局部坐标系下横坐标就为节点m的整体坐标系下的横坐标减去吊点节点n的前一个吊点节点n-1的横坐标（即吊点n-1即为节点m的局部坐标系原点）。第二步确定悬链线吊点节点n局部坐标系横坐标，当采用非吊点节点公式得出的竖向位移为零时（因为吊点节点均为悬链线起点，其竖向位移按自己坐标系竖向位移均为0，为了计算下一坐标的起点竖向位置，此处应该按照上一段悬链线的终点来计算竖向位移），则相应的节点的局部坐标系横坐标就为节点的整体坐标系下的横坐标减去对应吊点前两个吊点xi-2的横坐标（例如吊点节点i-1，不小于其横坐标值的节点为xi，因而其原点坐标为xi-2）。

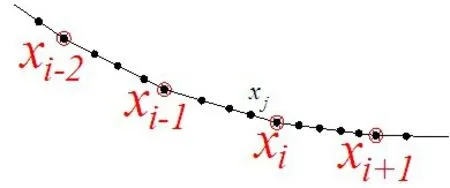
图3 节点坐标查找图示

其次，根据局部坐标系横坐标值及相应k，可以求出相应局部坐标系下的竖向位移值，同时使用Excel求出此局部坐标系原点位于整体坐标系中的位置。每个i段悬链线上节点竖向整体坐标就等于前面i-1段悬链线竖向位移的总和加相应局部坐标。

1.3 有限元模型求解

1.3.1 有限元软件求解悬索桥成桥线形步骤

本文主要采用迈达斯以及大型通用有限元软件ANSYS进行分析，建立模型的步骤和方法基本一致，主要步骤如下：①建立有限元几何模型。根据初步拟定的结构尺寸以及确定的矢跨比以及跨度信息，主缆节点先根据结构信息按照抛物线拟定一个初步线形。

②按照抛物线线形及初始设计参数计算一个初始主缆水平力[7]：

③根据初始的主缆水平力和节点坐标反算每个主缆单元初始轴力。④将整体模型的吊索位置换成弹性支承，采用多点弹性支承连续梁模型计算出每个主梁吊点位置的竖向支反力作为吊杆的初始内力。⑤试算调整H0数值的大小，随后更新主缆节点坐标、主缆单元内力以及吊杆内力，使得所有主缆节点竖向位移计算完成后的竖向变形趋于零。⑥此时得出的主缆节点坐标即为成桥主缆线形节点坐标，试算得到的H0为成桥主缆水平力。

1.3.2 主缆调索直观表述

悬索桥成桥线形的有限元模型调索过程可结合图4形象地描述如下：悬索桥主缆右端IP点固定于支座2，左端IP点位置施加大小为H的水平作用力，通过不断调整左端的水平力H的大小（相当于试算过程中不断调整1.3.1中第5步中的H0数值大小）以及吊杆的初始力（更新吊杆初始内力实际上是改变吊杆无应力长度）使得主缆所有节点竖向位移接近为零，主缆在整个调索过程中节点位移不断变化则可看做不断更新主缆节点初始坐标。当所有节点在成桥荷载作用下的竖向位移趋于零时，初始输入的主缆节点形成的主缆线形即为主缆成桥线形[8]。

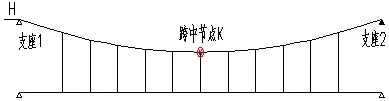
图4 索力调整示意图

2 算例分析

2.1 算例模型介绍

算例桥梁采用双塔中间悬挂曲线悬索桥体系如图5所示，主缆两IP点跨径为75 m，矢跨比1/16。主梁采用扁平钢箱梁，桥面总宽为4.6 m，主梁梁高为0.8 m，吊索按5.7 m等间距布置，如图6所示。主缆在塔顶上采用耳叉式锁扣与主塔连接，主塔背部通过分散的两根背索把索力传递到主塔及背索锚碇上，桥梁纵断面按最小净空5.0 m要求进行控制。

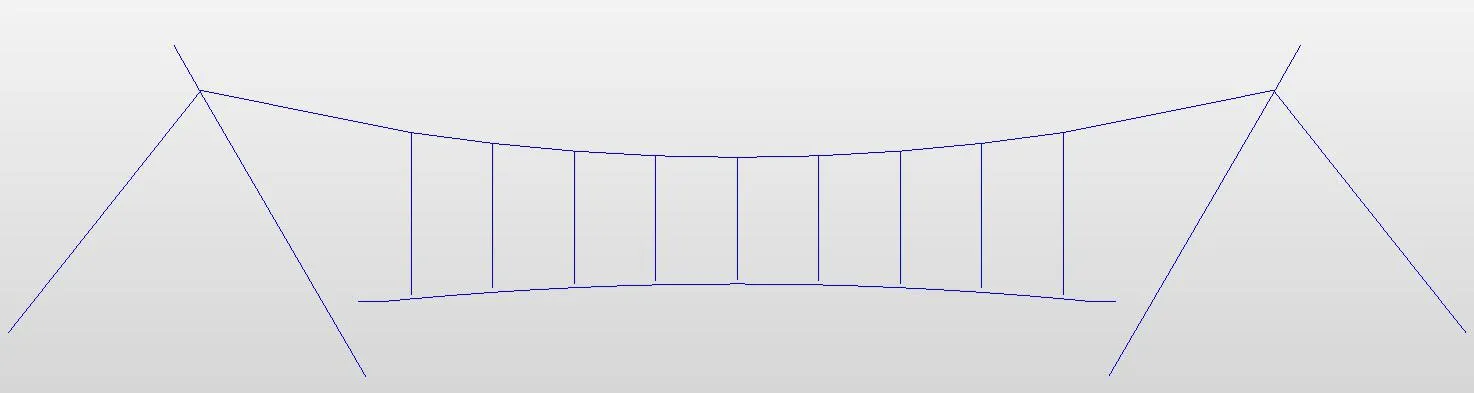
图5 全桥M idas有限元模型

桥梁主要构件使用的材料类型及尺寸如下，主缆：6×19W+IWR-40钢丝绳22根；吊杆：6×19W+IWR-40钢丝绳1根；主梁：Q345钢箱梁。

2.2 结果比较

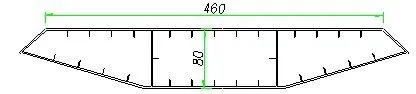
图6 桥梁主梁断面（单位:cm）

通过前文所述3种（两类）计算方法，按照相应计算步骤，可分别求出算例桥梁对应的计算结果，现将主要计算结果列表，如表1～3。主要包括主缆水平力，主缆节点坐标以及吊杆内力（分段悬链线吊杆内力分别由两种有限元模型计算出后代入相应总体计算模型），结果如下。

通过对比计算结果可以看出：①3种计算方法得出的主缆水平分力基本一致，差值在0.35%以内；②主缆节点坐标计算值吻合度高，竖向坐标差值都不大于5 mm；③吊杆内力值差值除2号及8号吊杆相差1.11%以外，其余均在0.75%以内。

从各项主要计算结果可以看出，3种计算方法均能得到较好的结果。在计算过程中分段悬链线结合Excel的方法速度更快；其他两种方法步骤较为繁琐，容易出错，求解时间更长。但分段悬链线方法需要借助有限元提供的吊索内力，不能够单独的计算。因此结合两者进行求解能够高效精准的求出悬索桥的成桥线形。此外主缆的空缆线形同样可采用段悬链线结合Excel的方法求解，由于空缆线形求解过程无吊杆内力的影响，分段悬链线方法可直接根据参数利用单悬链线线型公式求解，求解更加快捷和方便。