斜拉桥施工控制张拉力的计算方法研究

李炎， 陈常松， 董道福

(1.长沙理工大学， 湖南 长沙 410114； 2.江西省交通运输科学研究院有限公司； 3.江西省桥梁结构重点实验室)

在斜拉桥施工全过程分析中，首先需要提供一组斜拉索控制张拉力，使得计算成桥状态与设计合理成桥状态一致。中国学者基于影响矩阵法提出了很多控制张拉力的确定方法：淡单辉提出基于影响矩阵及粒子群算法的斜拉桥自动调索方法；贾丽君建立了求解线形问题拉索施工控制张拉力的影响矩阵方程，在考虑结构非线性效应和徐变、收缩效应的基础上，通过迭代的方式实现了非线性问题施工控制张拉力的求解；冯仲仁基于线性影响矩阵理论，通过正装分析方法模拟斜拉桥施工过程对控制张拉力的影响，得到满足设计成桥索力准确计算施工控制张拉力的方法等。传统的斜拉桥施工控制张拉力计算方法通常需要耗费大量时间进行反复试算，却又难以获得十分理想的结果。

该文提出采用无应力索长值作为张拉控制参数进行斜拉桥无应力构形迭代求解，主要求解思路为：① 根据设计成桥状态计算(不计入施工过程效应)设计无应力索长；② 以设计无应力索长作为张拉条件，可求解不同施工工序下对应的控制张拉力；③ 采用控制张拉力进行成桥状态分析时，成桥索力与设计成桥索力相对百分差值一般均在±5%以内(成桥锚点坐标与设计一致)，由于计算成桥状态下的索力值与设计合理成桥状态下的索力值之间存在一定的差别，因此需要重新计算该成桥状态下的无应力索长值，作为斜拉索下料长度的数据；④ 如果还需要对成桥状态进行调整，可通过斜拉索的控制张拉力进行调整，调整后将得到新的成桥状态及斜拉索的下料长度。该方法在控制张拉力求解过程中计入徐变、收缩及几何非线性效应的影响。

该文以湖北嘉鱼长江公路大桥为工程背景，运用无应力构形法对不同张拉工序的控制张拉力进行求解，分别将控制张拉力代入模型计算至成桥状态，并对比分析计算与设计成桥状态之间的差异，以验证无应力构形法的可行性。

1 施工控制张拉力求解理论

斜拉桥属于高次超静定结构，在斜拉桥施工全过程分析计算中，可采用无应力构形计算理论，用来求解钢箱梁的无应力制作尺寸，也是保证最终成桥状态是否能够达到设计成桥状态的关键计算理论之一，索力及索形的求解则基于悬链线解析理论，该理论在该文方法的运用中起着至关重要的作用。

1.1 斜拉索悬链线索元计算理论

根据悬链解析理论可知，在自重荷载作用下悬链线的几何关系式为：

(1)

(2)

(3)

式中：E为斜拉索的弹性模量；A为无应力横截面面积；w为单位无应力索长的重量；Lx、Ly为斜拉索在x、y方向上的投影长度；Lu为无应力索长；L为有应力索长；Fix、Fiy为i端索力在x、y方向上的分量；Fjx、Fjy为j端索力在x、y方向上的分量；Ti、Tj为i、j节点处的索力。

根据悬链线计算理论可知：斜拉桥合理成桥索力对应的无应力索长是唯一的，因此合理成桥状态一旦确定，斜拉索的无应力索长也是确定的。在已知斜拉索的E、A、w、Lx、Ly情况下，求解单索问题可分为两类：① 第一类单索问题：已知Lu，求索形和索力；② 第二类单索问题：已知Fix、Fiy、Fjx、Fjy、Ti、Tj、αi、αj中的一个，求解索形和其他索端力分量。

各参数意义见图1。

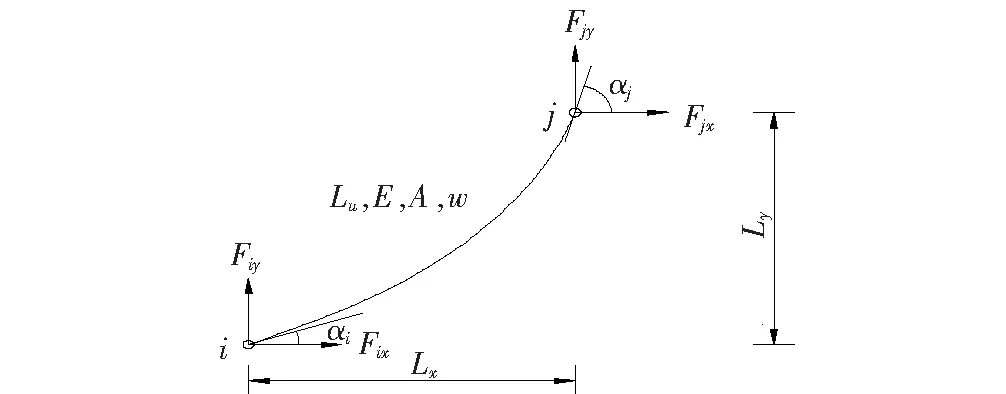
图1 悬链线索单元图

在斜拉桥全过程模拟分析中，斜拉索的张拉可以采用索长参数控制或索力参数控制，还可以两种参数混合控制。采用无应力索长值作为张拉控制参数进行控制时，柔性迭代可以根据无应力索长和锚点坐标，求解对应的索形、索端力和切线刚度矩阵，其中索端力迭代修正公式为：

(4)

(5)

式中：K为单元的切线刚度矩阵；{ΔLxΔLy}T为索长投影的误差向量。

采用索力值作为张拉控制参数时，需要反复调用上述求解过程求解Lu，再通过无应力索长求解索形和索力。

1.2 无应力构形迭代求解

无应力构形常用求解方法有正装迭代法、倒拆法或正装-倒拆迭代法等。由于倒拆分析在处理混凝土构件的收缩徐变时出现不闭合现象，因此该文采用正装迭代法进行无应力构形迭代求解斜拉索施工控制张拉力。首先采用无应力索长值作为张拉控制条件，然后一次性激活除合龙段以外的其他所有主梁对应单元，初始计算构形为设计合理成桥构形，按照施工过程分阶段激活自重荷载和外荷载，最终成桥状态下节点坐标偏离设计值，因此将各节点累计位移反号加到设计坐标作为下一轮正装计算的初始构形坐标，如此反复迭代(该迭代过程始终采用无应力索长值作为控制参数)。迭代初始构形计算表达式如下：

ymc=ys-fm-1

(6)

xmc=xs-dm-1

(7)

式中：xmc和ymc为第m轮计算构形初始坐标；xs和ys为设计坐标；fm-1为第m-1轮计算节点竖向累计位移；dm-1为第m-1轮计算节点纵向累计位移。

通常情况下，上述迭代收敛是以成桥节点坐标与设计坐标之间的偏差值小于某个收敛精度作为收敛条件，为了缩短计算控制张拉力的时间，采用成桥索力与设计成桥索力相对百分差值作为迭代收敛条件，整个迭代收敛条件为：

(8)

式中:Tm为第m轮迭代计算成桥索力；Ts为设计成桥索力；ε1为收敛精度，一般取值为0～0.05。

2 各施工阶段控制张拉力求解

设计施工流程往往是参照常规施工流程，但是实际施工过程中需要根据施工条件等因素对施工流程进行优化，在满足施工控制精度(合理成桥状态)及确保施工过程结构安全的前提下尽量节约建造成本。通常实际施工流程与设计图纸上施工流程有所差别，因此需要重新计算一组满足实际施工工序的张拉力。

2.1 施工控制张拉力的确定

针对目前控制张拉力的求解方法，该文提出采用基于无应力构形控制法的索力求解方法，该方法是采用无应力索长值作为张拉控制参数进行无应力构形迭代计算，从而得到满足合理成桥状态的控制张拉力。

(1) 控制张拉力的确定过程

通过悬链线理论对设计图纸中的无应力索长进行校核，将满足合理成桥状态下的无应力索长作为斜拉索最后一次张拉控制的索长，一张则采用在设计索长基础上增加一定长度值(考虑锚具锚固所需的长度)作为张拉参数，该文常规计算初张力的流程为：

第1步：将设计图纸中的无应力索长作为斜拉索张拉控制索长。

第2步：将斜拉索控制索长增加一定长度值作为斜拉索的初张索长。

第3步：将初张索长和控制索长代入无应力构形求解模型进行迭代求解施工张拉控制索力。

第4步：循环迭代至计算成桥索力与设计成桥索力相对百分差值在5%以内，则停止进行下一步迭代(图2)，提取该状态下斜拉索的一张和二张索力即为斜拉桥各施工阶段张拉控制索力。

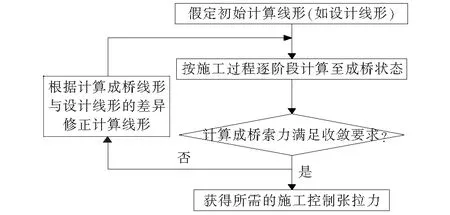
图2 控制张拉力迭代求解过程

(2) 斜拉索制作长度的确定过程

在斜拉桥施工控制张拉力确定的前提下，斜拉索制作长度的计算就变得相对简单，具体计算流程如下：

第1步：将上述分析得到的张拉控制索力代入斜拉桥全过程正装分析模型中(模型初始构形需考虑各节点受力状态下预抬和预偏值)，计算分析至成桥状态(节点坐标均达到设计成桥坐标)。

第2步：利用计算成桥索力、成桥锚点坐标、斜拉索弹性模量和单位索重等参数，通过悬链线计算理论分析得到斜拉索的无应力长度。

上述分析过程是不设置成桥塔偏，如果需要设置成桥塔偏，第1步中索塔初始构形的纵向坐标采用设计值，可通过调整成桥索力的方式来调整成桥塔偏，分析过程均可由程序自动计算实现，也可以通过手动计算进行校核。

2.2 控制张拉力的计算分析工况

在斜拉桥各构件无应力状态量一定的条件下，其成桥索力并不受斜拉索张拉次数的影响，故采用斜拉索一次张拉到位，具体计算工况如表1所示。

采用表1中钢箱梁悬拼工序进行斜拉桥的全桥建模，然后通过迭代求解出斜拉索的一张索力(施工控制张拉力)，为了保证实际成桥构形满足设计构形要求，在全桥合龙后需要对斜拉桥的尾索进行调索。

表1 钢箱梁悬拼计算工况

3 工程应用实例

湖北嘉鱼长江公路主桥是一座全桥长1 650 m，主跨920 m的混合梁斜拉桥，采用空间双索面，南北塔各设置30对斜拉索，采用预制平行钢丝整体索，跨度组合为(70+85+72+73) m+920 m+(330+100) m，其中北边跨总跨度为300 m，主桥北边跨采用预应力混凝土箱梁，中跨和南边跨采用钢箱梁，钢混结合段长度为8.5 m。索塔横桥向采用钻石形，南塔高265.9 m，北塔高262.2 m。整体桥型布置图如图3所示。

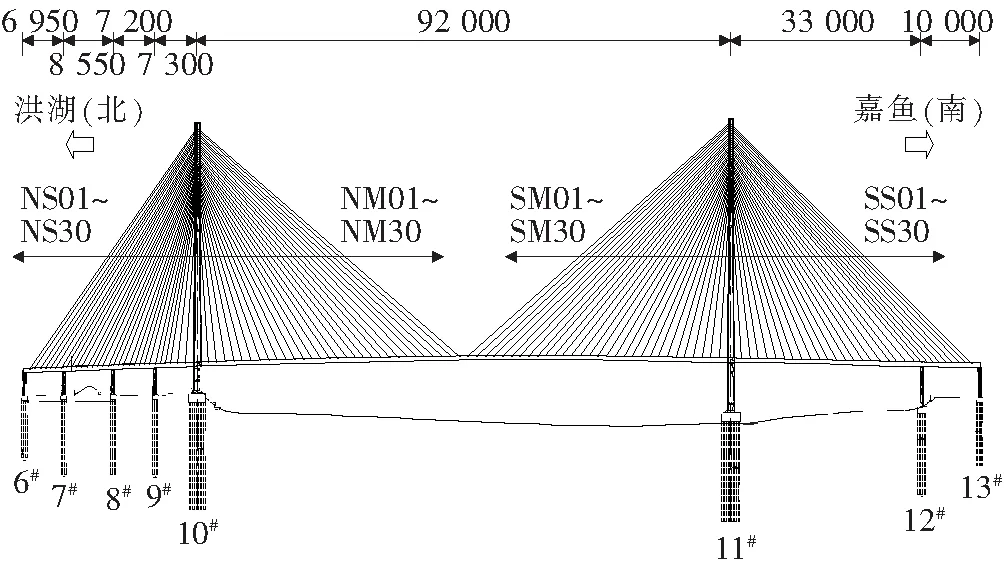
图3 嘉鱼长江公路大桥桥型布置图(单位：cm)

3.1 施工控制张拉力计算分析

嘉鱼长江公路大桥跨径大，结构非线性效应明显，采用常规试算调索法进行施工阶段索力计算需要花费大量时间，因此该文提出无应力构形迭代的方式求解施工控制张拉力。图4为施工过程中的安装索力，该桥拟定在合龙后对NS30、NM30、SM30、SS30、NS29、NM29、SM29和SS29号斜拉索进行调索，从而使得最终成桥状态满足设计要求。

3.2 成桥状态对比分析

由于施工控制张拉力是以设计成桥状态为目标计算而来，因此采用上述分析所得控制张拉力(不包括合龙后调索索力)进行成桥状态计算，并将计算成桥状态与设计成桥状态进行对比分析，具体结果如下。

图4 施工控制张拉力

(1) 成桥索力对比

成桥索力对主梁内力及线形影响较大，故将该成桥状态与设计成桥状态进行比较，其中计算成桥索力与设计成桥索力的对比数据如图5所示。

图5 成桥索力相对百分差值

由图5可知：该文方法计算成桥索力与设计成桥索力最大相对百分差值出现在SM30号斜拉索，且最大差值为4.70%，因此该文方法能够保证计算成桥索力与设计成桥索力相对百分差值均在5%以内。

(2) 主梁内力对比

对计算成桥状态下与设计成桥状态下，主梁的轴力、剪力和弯矩进行比较，结果如图6～8所示。

由图6～8可知：两种成桥状态下，各主梁单元的轴力和弯矩曲线吻合较好，其中边跨混凝土箱梁单元的单元轴力值最大相差46 795 kN，相对百分差值为13.24%，钢箱梁单元轴力值最大相差4 936 kN，相对百分差值为3.22%，边跨混凝土箱梁单元的剪力值最大相差1 689 kN，相对百分差值为7.16%，钢箱梁单元的剪力值最大相差624 kN，相对百分差值为17.89%，边跨混凝土箱梁单元的弯矩值最大相差9 992 kN·m，相对百分差值为26.95%，钢箱梁单元的弯矩值最大相差8 196 kN·m，相对百分差值为15.88%，由内力分析结果可知：计算成桥状态与设计成桥状态吻合良好，按照该文方法计算张拉力进行施工控制张拉，理论上能够保证最终成桥受力状态达到设计状态。

图6 主梁成桥轴力值比较

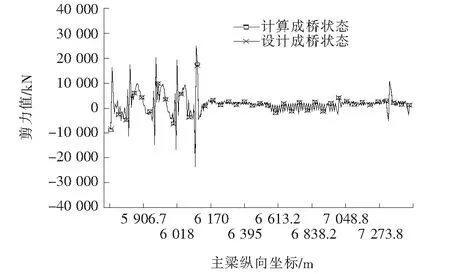
图7 主梁成桥剪力值比较

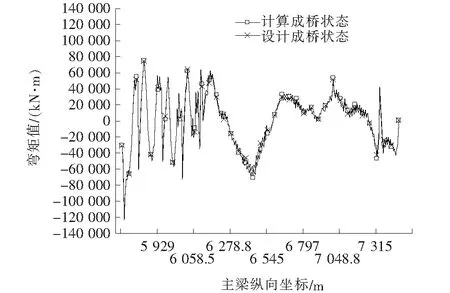
图8 主梁成桥弯矩值比较

4 结论

(1) 采用无应力索长值作为张拉控制参数进行无应力构形迭代求解施工控制张拉力，该求解过程简单明确，且便于实现程序化自动调索计算，能够较好地满足设计及施工控制计算分析。

(2) 分析结果表明：该文方法分析出的施工控制张拉力计算成桥状态与设计成桥状态基本一致，其中成桥索力之间的误差均控制在5%以内，该方法能够较好地计算出满足设计成桥状态的施工控制张拉力。