关于不定方程x2-2y4=M(M=17，41，73，89，97)

管 训 贵

(泰州学院数理学院，江苏 泰州 225300)

1 引言及主要结论

设D，M为给定的整数，且D>0为非平方数，N(D，M)表示不定方程

x2-Dy4=M

(1)

的正整数解的组数.研究不定方程(1)的正整数解是数论中的一类重要课题．

1968年，Cohn[1]证明了：N(5，44)=1，(x，y)=(7，1)；N(5，11)=2，(x，y)=(4，1)，(56，5)；N(5，-44)=3，(x，y)=(6，2)，(19，3)，(181，9)．

1983年，Tzanakis[2]对不定方程(1)进行了系统研究，并且证明了：

定理1a)N(2，17)=0，在y≡0(mod 8)时；b)N(2，41)=0，在y≡0(mod 8)时；c)N(2，73)=0，在2|y且y

≡

0(mod 3)时；d)N(2，89)=0，在y≡0(mod 16)时；e)N(2，97)=0，在y≡0(mod 8)时．

后来，文献[3-11]相继证明了：N(3，46)=2，(x，y)=(7，1)，(17，3)；N(3，22)=2，(x，y)=(5，1)，(85，7)；N(3，286)=2，(x，y)=(17，1)，(23，3)；N(7，93)=2，(x，y)=(10，1)，(130，7)；N(22m+1，-22m)≤3；N(a2+1，-2a)≤3；N(a2+1，3-4a)≤5；N(a2+1，35-12a)≤4；N(a2+1，8-6a)≤4．

然而，定理1至今尚未得到改进.本文运用递归序列、同余式以及平方剩余的有关性质完全解决了这一问题，即证明了如下结果．

定理21)N(2，17)=2，(x，y)=(7，2)，(23，4)；

2)N(2，41)=0；

3)N(2，73)=0；

4)N(2，89)=2，(x，y)=(11，2)，(91，8)；

5)N(2，97)=0．

2 定理的证明

1)设相应的不定方程为

x2-2y4=17，

(2)

易知，方程X2-2Y2=17的一般解可由以下两个非结合类给出：

(3)

或

(4)

不妨设X≥0，Y≥0，则(3)式中只需考虑“+”号，而(4)式中只需考虑“-”号即可.若方程(2)有整数解，必有n，使得

y2=2un+5vn

(5)

或

y2=-2un+5vn，

(6)

根据文献[10]，可得下列关系：

un+2=6un+1-un，u0=1，u1=3；

vn+2=6vn+1-vn，v0=0，v1=2；

(7)

um+n=umun+2vmvn，vm+n=umvn+vmun；

(8)

u-n=un，v-n=-vn；

(9)

v2n=2unvn，

(10)

un+2kt≡(-1)tun(moduk)，

vn+2kt≡(-1)tvn(moduk)；

(11)

un+2kt≡un(modvk)，vn+2kt≡vn(modvk).

(12)

见表1.

表1 n,un,vn的关系Tab.1 The relationship between n,un,vn

n101112131415un22619537131836323768398401447855408326102926097152139002499vn1599442893222358543339720316681596218457556052107578520350

先讨论(5)式(为节省篇幅，下文中的“T”表示取模后所得剩余序列的周期).

情形1n≡1(mod 60)且n≠1.可令n=1+5·2s(2k+1)(s≥2)，则由(5)式结合(8) 式、(11)式和表1，可得

y2≡±(2u1+5·2s+5v1+5·2s)(modu5·2s) ≡

±23v5·2s(modu5·2s)≡±23v2s(modu2s).

(13)

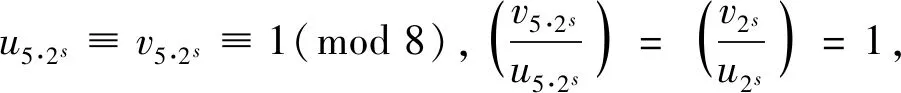
(14)

情形2n≡49(mod 60).可令n=2·2(k+1)·15-11，则由(5)式结合(9)式、(11)式和表1，可得

y2≡2u-11+5v-11(modu15) ≡2u11-5v11(modu15) ≡

-202439144(mod 32·11·19·59·601·2281).

情形3n=1时，由(5)式得y=4，故方程(2)有正整数解(x，y)=(23，4)．

再讨论(6)式．

利用(7)式，对(6)式同样取模8、模3得T=4，排除n≡0，2，3(mod 4)，剩n≡1(mod 4).

情形1n≡1(mod 20)且n≠1.可令n=1+2s(2k+1)(s≥2)，则由(6)式结合(8)式、(11)式和表1，可得

y2≡±(-2u1+2s+5v1+2s)(modu2s)≡

±7v2s(modu2s).

(15)

(16)

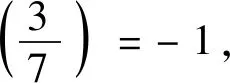
情形2n≡5，-7，-3(mod 20).可分别令n=2·2k·5+5，n=2·2k·5-7 及n=2·2k·5-3，则由(6)式结合(9)式、(12)式和表1，可得

y2≡-2u5+5v5，-2u-7+5v-7，

-2u-3+5v-3(modv5) ≡

-2u5，-2u7-5v7，-2u3-5v3(modv5)≡

-6726，-22·158099，

-22·137(mod 2·29·41)．

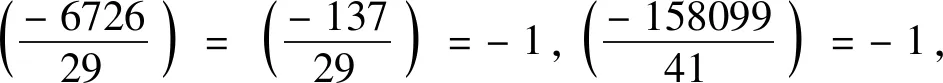
情形3n≡9(mod 20).可令n=2·k·10+9，则由(6)式结合(11)式和表1，可得

y2≡±(-2u9+5v9)(modu10)≡

±22·1489813(mod 17·241·5521)．

情形4n=1时，由(6)式得y=2，故方程(2)有正整数解(x，y)=(7，2)．

综上，方程(2)仅有正整数解(x，y)=(7，2)，(23，4)．

2)设相应的不定方程为

x2-2y4=41.

(17)

易知，方程X2-2Y2=41的一般解可由以下两个非结合类给出：

或

若方程(17)有整数解，必有n，使得

y2=2un+7vn

(18)

或

y2=-2un+7vn.

(19)

先讨论(18)式．

令n=2(2k+1)·3+1，则由(18)式结合(11)式和表1，可得

y2≡-(2u1+7v1)(modu3)≡-20(mod32·11)．

再讨论(19)式．

利用(7)式，对(19)式同样取模8、模3得T=4，排除n≡0，1，2(mod 4)，剩n≡3(mod 4)；又对(19)式取模5得T=6，排除n≡0，1，3，4(mod 6)，剩n≡2，5(mod 6)，即n≡2(mod 3).因此n≡11(mod 12)．

令n=2·2(k+1)·3-1，则由(19)式结合(9)式、(11)式和表1，可得

y2≡-2u-1+7v-1(modu3)≡-20(mod 32·11)．

综上，方程(17)没有正整数解．

3)设相应的不定方程为

x2-2y4=73.

(20)

易知，方程X2-2Y2=73的一般解可由以下两个非结合类给出：

或

若方程(20)有整数解，必有n，使得

y2=2un+9vn

(21)

或

y2=-2un+9vn.

(22)

先讨论(21)式．

令n=2(2k+1)·3+1，则由(21)式结合(12)式和表1，可得

y2≡2u1+9v1(modv3)≡24(mod 2·5·7)．

再讨论(22)式．

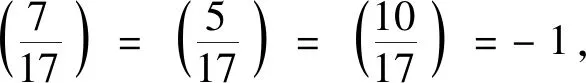
令n=2·k·4+1，则由(22)式结合(12)式和表1，可得

y2≡-2u1+9v1(modv4)≡12(mod 23·3·17)．

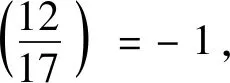
综上，方程(20)没有正整数解．

4)设相应的不定方程为

x2-2y4=89.

(23)

易知，方程X2-2Y2=89的一般解可由以下两个非结合类给出：

或

若方程(23)有整数解，必有n，使得

y2=4un+11vn，

(24)

或

y2=-4un+11vn.

(25)

先讨论(24)式．

若n≡8(mod 20)，可令n=2·(k+1)·10-12，这里k为非负整数，则由(24)式结合(9)式、(11)式和表1，可得

y2≡±(4u-12+11v-12)(modu10)≡

±(4u12-11v12)(modu10) ≡

∓22·725785829(mod 17·241·5521).

(26)

由n≡0(mod 4)，n≡0(mod 3)以及n≡0(mod 5)知n≡0(mod 60)．

若n≠0，令n=0+2×(3k±1)×5×3t，取m为3t与5×3t中之一(t≥1)，则由(9)～(11)式得

y2=4un+11vn≡±(4u±2m+11v±2m)≡

±(4u2m±11v2m)(modu3m) ≡

(27)

(28)

对11um+8vm，取模79得T=13：11，49，46，69，52，6，63，56，36，2，55，12，17，11，49，….而m模13的T=3，令

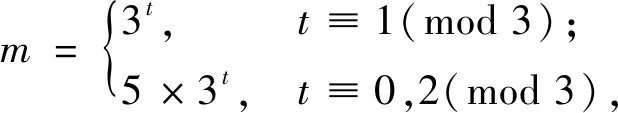
对11um-8vm，取模79得T=13：11，17，12，55，2，36，56，63，6，52，69，46，49，11，17，….而m模13的T=3，令

当n=0时，得到方程(23)的正整数解(x，y)=(11，2)．

再讨论(25)式．

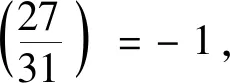
由n≡2(mod 4)，n≡2(mod 5)以及n≡2(mod 3)知n≡2(mod 60)．

若n≠2，令n=2+2×(4k±1)×3×5×2t，取m为2t与5×2t中之一(t≥1)，则由(9)～(11)式得

y2=-4un+11vn≡-4u2±6m+11v2±6m≡

-4(u2u±6m+2v2v±6m)+11(u2v±6m+v2u±6m)≡

-4(17u6m±24v6m)+11(±17v6m+12u6m)≡

-4(17u-2m±24v-2m)+11(±17v-2m+12u-2m)≡

-4(17u2m∓24v2m)+11(∓17v2m+12u2m)≡

64u2m∓91v2m≡∓91v2m(modu2m)．

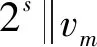
于是得

(29)

对um取模13得T=14：1，3，4，8，5，9，10，12，10，9，5，8，4，3，1，3，…．而m模14的T=3，令

当n=2时，得到方程(23)的正整数解(x，y)=(91，8)．

综上，方程(23) 仅有正整数解(x，y)=(11，2)，(91，8).

5)设相应的不定方程为

x2-2y4=97.

(30)

易知，方程X2-2Y2=97的一般解可由以下两个非结合类给出：

或

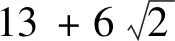
若方程(30)有整数解，必有n，使得

y2=6un+13vn

(31)

或

y2=-6un+13vn.

(32)

先讨论(31)式．

再讨论(32)式．

令n=2·2k·3+3，则由(32)式结合(11)式和表1，可得

y2≡-6u3+13v3(modu3)≡

13v3(modu3)≡910(mod 32·11)．

综上，方程(30)没有正整数解.定理得证．