单机随机排序问题的WSEPT规则近似∗

王艳红 雷松泽 张文娟 李 蕊

（1.西安工业大学理学院 西安 710021）（2.西安工业大学计算机科学与工程学院 西安 710021）

1 引言

排序问题也称调度问题，实际问题中，常有一些随机因素，或者随机数据在进行决策之前不确定，这些随机因素或者随机数据即为随机变量，随机变量在进行决策之前只知（或能统计出）其概率分布律，分布函数，均值和方差等。此类包含随机变量的排序问题即为随机排序问题［1］。很多现实问题中的参数是连续变化的，比如新任务的到达时间，资源衰退，任务的完工时间等。对于不确定性问题，很多近似算法已经被提出，如最优搜寻算法，蚁群算法，遗传算法，机器规划，基于寻找策略的人工智能，支配或启发式算法以及商业化的有限容量排序等。对于一些排序问题，将其分解为各个分支，每个分支采用不同的处理方式，把这些分支综合起来后可能会得到意想不到的效果及改善。给出随机排序问题（调度问题）的最优算法，可用于指导生产，优化生产。对于随机排序问题，由于随机变量的不确定性，常通过研究其对应的确定性问题来分析其最优算法。虽然一些随机排序问题对应的确定性问题是NP-难的，但原随机排序却有多项式最优算法。文献［2～3］证明了最短期望加工时间优先（Weighted Shortest Expected Processing Time First，WSEPT）规则为问题的最优算法，而该问题对应的确定性问题等价于背包问题［4～5］为 NP-难问题。

2 问题描述

本文对WSEPT规则在期望值角度给以新的更深入的分析。该分析对开始期限及完工期限模型均适用，包含两方面：一是E[μ (J)]［6］（其中 J 表示用WSEPT排序的随机任务集）的下界；二是（其中J表示用最优适应性策略排序的随机任务集）的上界。在此之后，通过由WSEPT的期望值与最优适应性策略排序的期望值的关系来修正上下界。

假设，在非适应性条件下，用WSEPT规则对任务进行排序。记Mj=∑μi，对所有的i≤j。根据马尔可夫不等式（马尔可夫不等式给出了随机变量的函数大于等于某正数的概率的上界），可得任务1，…，j的一个概率期望下界为1-Mj-1（对开始期望模型）及1-Mj（对完工期望模型）。但对于Mj-1≤1（或 Mj≤1）的情形，该下界仅限于小任务集。下述引理会给出一个更强的结论，当任务1，…，j-1已经成功排序后，通过计算期望值，任务j也能够被成功排序。例如，在完工期限模型中，可给出完工期限为1-tj-1-μj的概率下界。其中tj-1为当任务 j-1已在完工期限内完工时，任务1，…，j-1的总期望加工时间。因此，tj-1不会大于Mj-1，该新下界更强。

3 WSEPT规则下的E[ ]μ(J)上下界

引理1对于非适应性策略P，将任务 j的完工期限概率记为πj，将根据策略P排序的任务集记为J，则在开始期限模型中：

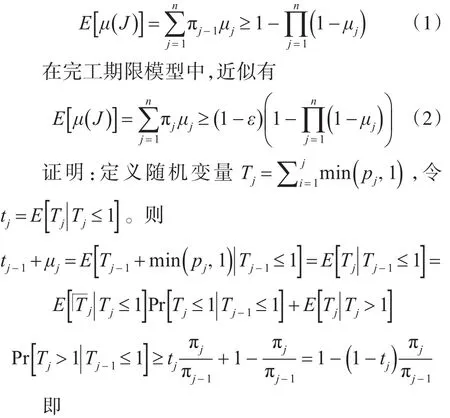
再考虑两种情形。对于所有的 j∈[]n，若μj≤1-tj-1，则有 μj≤zj≤1，故1-zj≥0 。由式（4）可得式（8）的界：

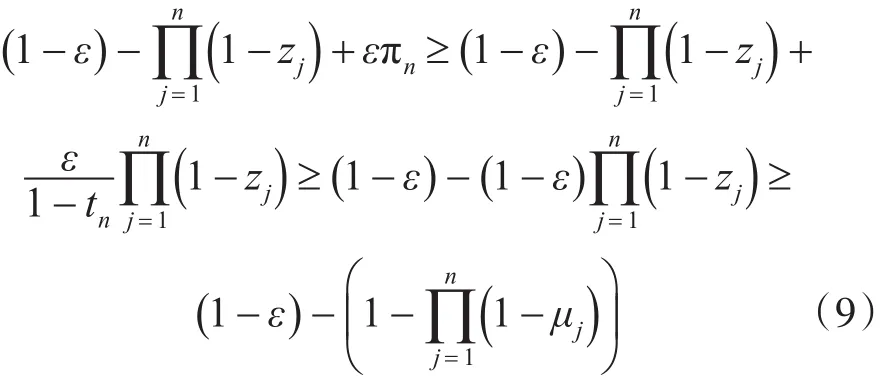
否则，对某个 k，若 μk+1＞1-tk，对于最小的k ，当 j≤k 时，有 μj≤zj≤1，由式（4）得［7］

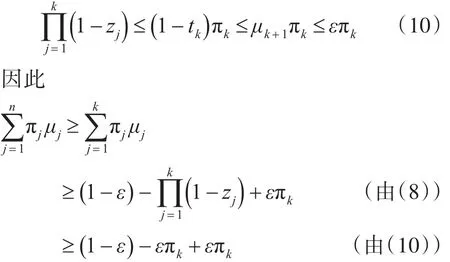
证毕。

引理2对于适应性策略P，将随机任务集记为 J，有

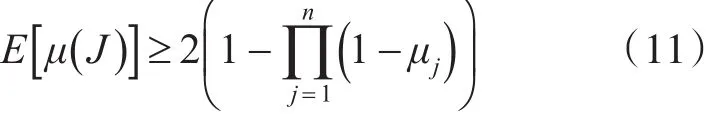
证明：假设P为相对于期限d的未来时间，任务集为R，将集合P从该点开始的随机任务集记为J(d，R)。对于任意任务集R及R中相互独立的任意随机变量t≤1时，对 ||R进行归纳，有

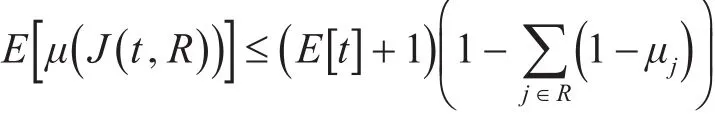
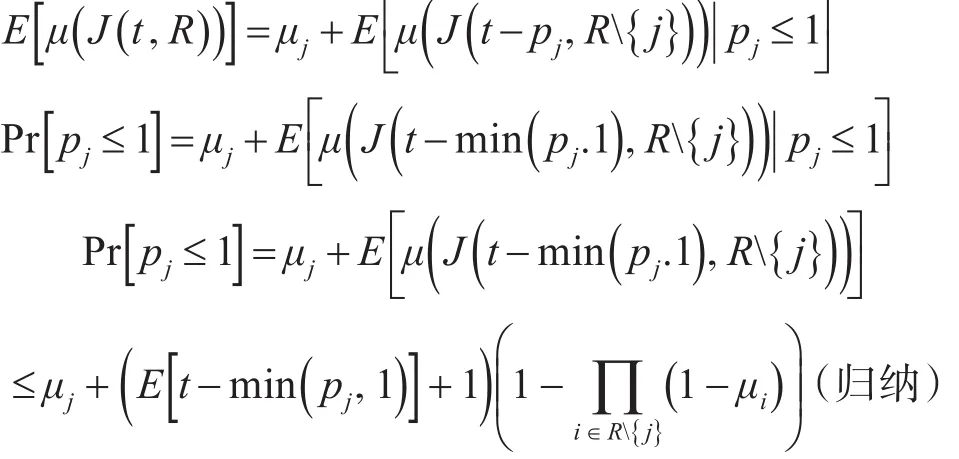
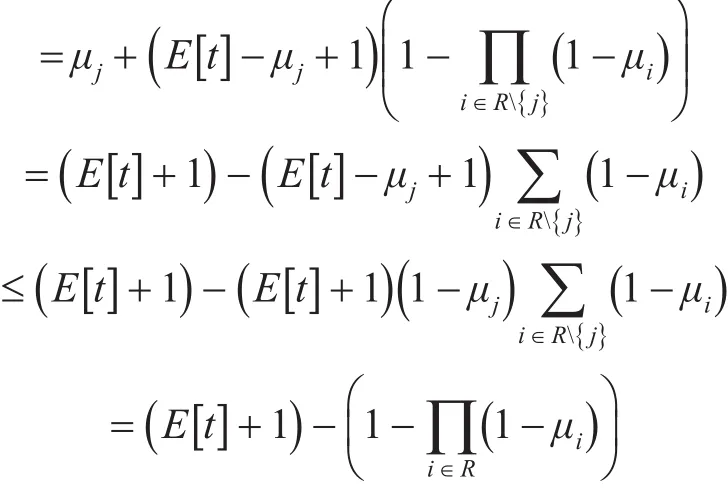
对∀j∈R成立，证毕。

4 WSEPT规则下的期望值上下界

下面讨论如何由WSEPT规则确定的期望值来获取更优的下界，以及由ADAPT规则获取更优的上界。在开始期限或完工期限模型中，用WSEPT规则对任务进行排序。若用Wj来定义开始期限模型中的wj及完工期限模型中的w′j，则WSEPT排序为定义［10］

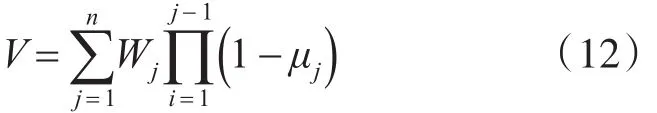
引理3在开始期限和完工期限模型中，ADAPT≤2V。

证明：对于一个最优的适应性策略P，用xj记P中的排序任务 j的概率。在开始期限和完工期限模型中，在开始期限模型中Wj=wj，在完工期限模型中Wj=w′j。若

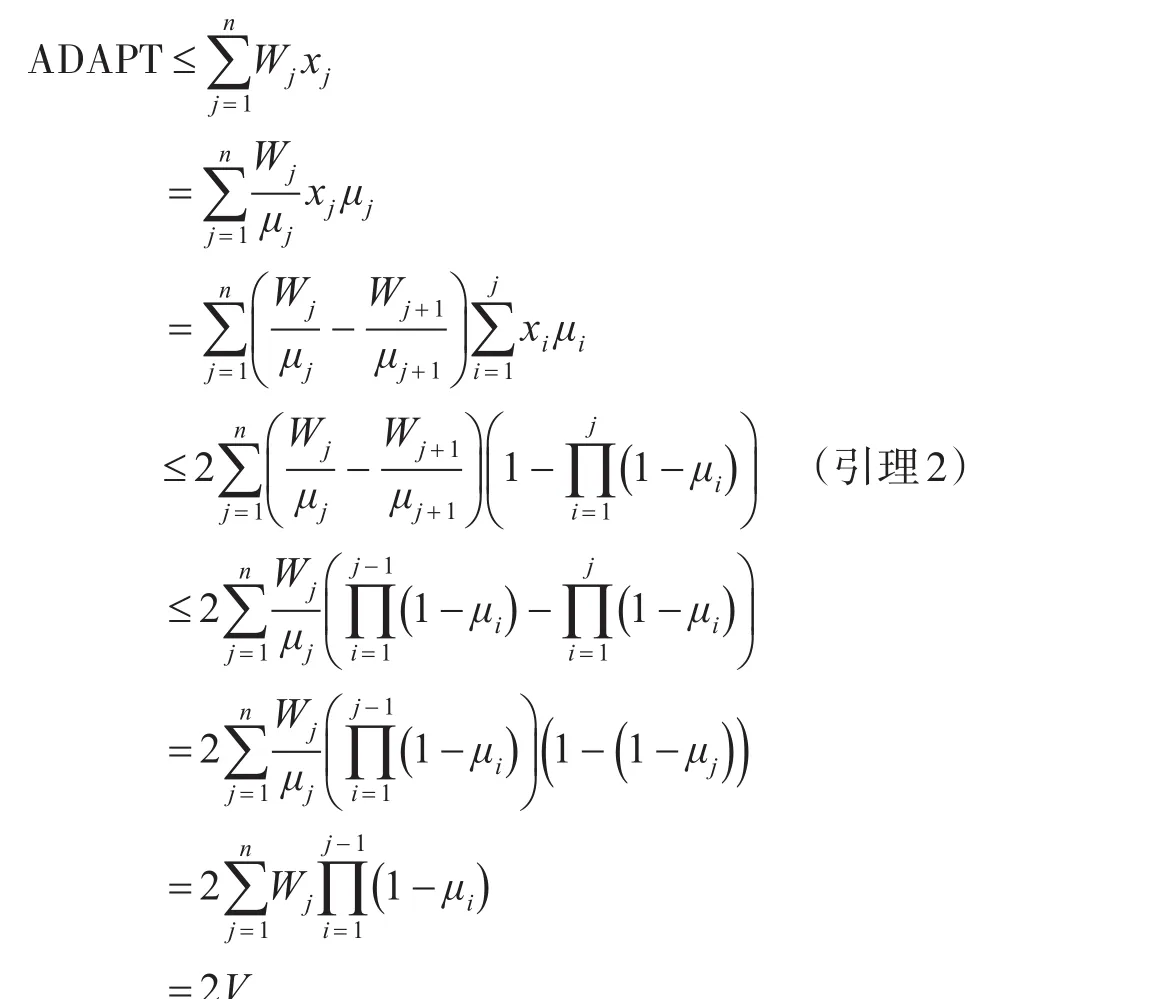
证毕。

引理4在开始期限模型中，由WSEPT规则确定的期望值至少为V。在完工期限模型中，由WSEPT规则确定的期望值至少为(1 -ε) V 。证明：根据WSEPT规则，用πj记在期限内完成的任务 j的概率。在开始期限模型中，得到的期望值为［13］

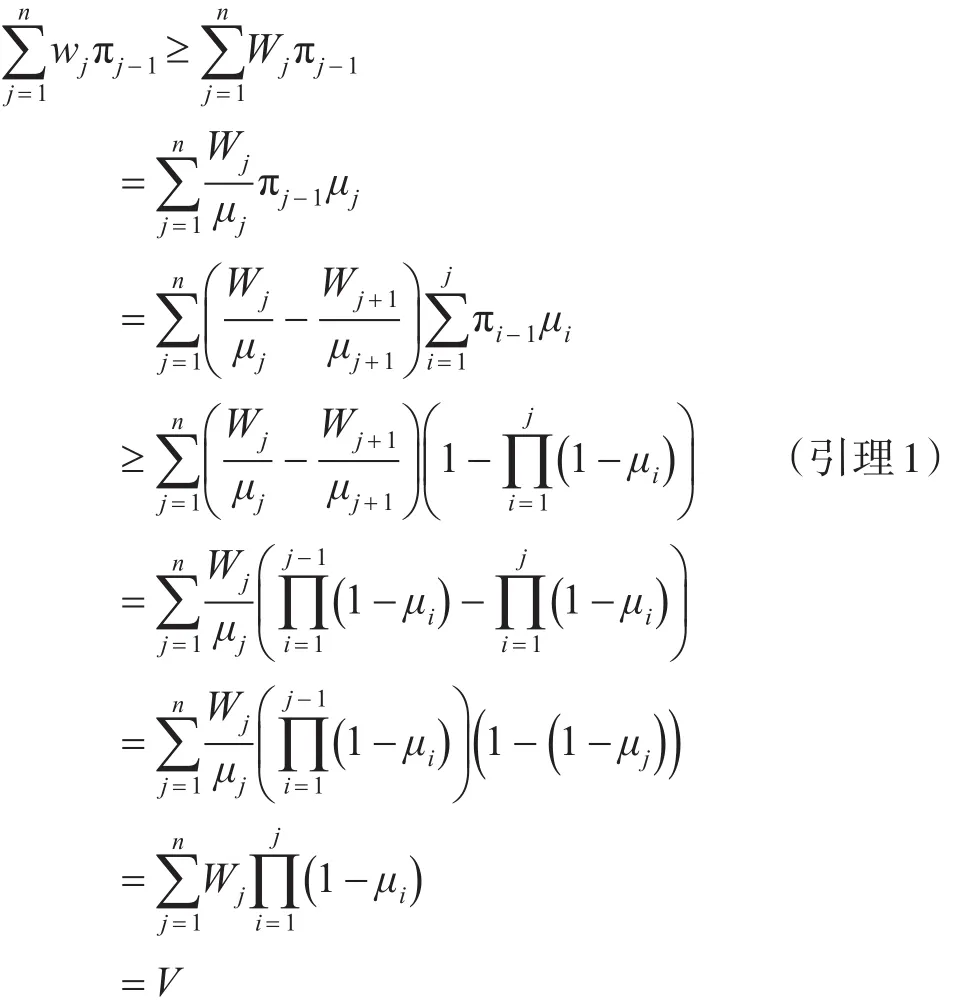
在完工期限模型中，由引理1可得，其期望值为(1 -ε) V 。

5 完工期限模型的4阶近似策略［14～15］

以上分析说明在开始期限模型中，WSEPT为一个2阶近似非适应性策略。在完工期限模型中，用以下两种解决方式能得到4阶非适应性策略。

1）若任务 j满足 w′j≥V 2，则仅排序这个任务。

2）否则，用WSEPT规则排序所有任务。

称之为最优2阶策略。

证明：若已排序一个任务，则得到期望值至少为V 2及ADAPT≤2V，故在该种情形下达到4阶近似。现考虑用WSEPT规则排序的情形，将在期限内完工的任务 j的概率记为πj，根据WSEPT规则，期望值为［16］

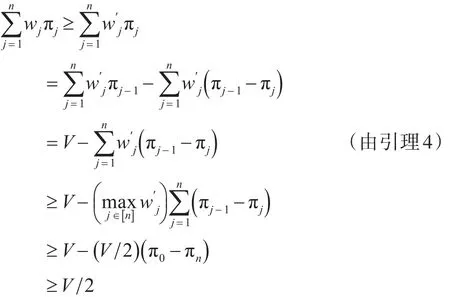
为4阶近似，证毕。

6 结语

为解决单机随机排序问题，本文对开始期限及完工期限两种模型，从期望值角度给出了其上下界，由WSEPT的期望值与最优适应性策略排序的期望值的关系来修正上下界。最终给出在完工期限模型下WSEPT规则的4阶近似程度分析。