一种伺服系统末端谐振抑制方法及试验

陈华锋

(中国船舶重工集团公司第七一三研究所，郑州 450015)

0 引 言

伺服系统也叫随动系统，是为了跟随某个运动过程而引入的一个反馈系统。它的特点是把位置、速度或加速度信号作为控制变量，并且从给定信号到反馈信号是一个闭环系统[1]。

伺服系统的应用领域决定了其最主要的工作模式是在位置模式，即位置的随动系统；其最重要的性能是跟随性能，即系统的输出快速、无差的跟随系统的输入指令。评价伺服系统跟随性的指标有很多，但最直接、最重要的就是系统带宽。系统带宽的高低直接决定了伺服系统跟踪给定信号的能力。系统带宽越高，其跟随给定信号变化的能力就越强，系统的动态特性就越好[2]。

在实际的伺服系统中，电机与负载之间通常是通过联轴器、变速箱、齿轮等传动装置相互连接，当传动轴的长度较长时，或者传动轴的刚性比较弱时，整个伺服控制系统的性能将会大大的下降。并且如果传动轴的两侧在系统运行的过程中存在形变，这样将会导致系统产生机械谐振现象。

这些弹性连接装置引入了机械谐振点，限制了系统刚度的提高，使得伺服系统在响应高频给定时谐振加剧，制约了位置伺服系统的带宽提升，不利于系统快速跟随性的提高，降低了伺服系统的工作效率[3]。

一个高性能伺服的系统结构和控制器设计需要满足伺服系统的跟随性能要求，同时具有一定的稳定性和抗扰性。因此，对伺服系统的固有机械谐振点的抑制变得非常重要[4]。

本文针对某装置伺服系统在等速运动时出现的谐振问题，设计了一种陷波滤波器，采用FFT频谱分析法获取谐振频率信号，最后通过试验验证了所述滤波器的有效性。

1 系统组成及存在的问题

伺服系统传动装置结构图如图1所示，包括伺服电机、减速器、负载以及弹性环节和齿隙环节。伺服电机通过减速器、驱动齿轮、大齿圈，连接负载。将传动刚度不足引起的弹性环节包含在从减速器到驱动齿轮间，齿隙环节主要存在于驱动齿轮与大齿圈间。

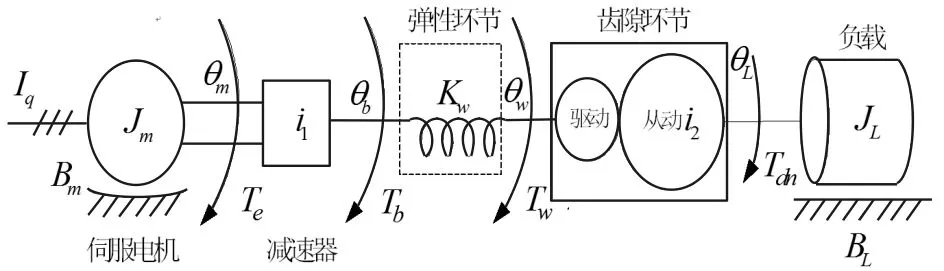
图1 伺服系统传动装置结构图

在针对该伺服系统进行等速运动试验时发现，在加速和减速过程中会出现抖振现象。图2、图3、图4分别为等速运动时位置环指令速度曲线、位置环输出速度曲线、位置误差曲线。

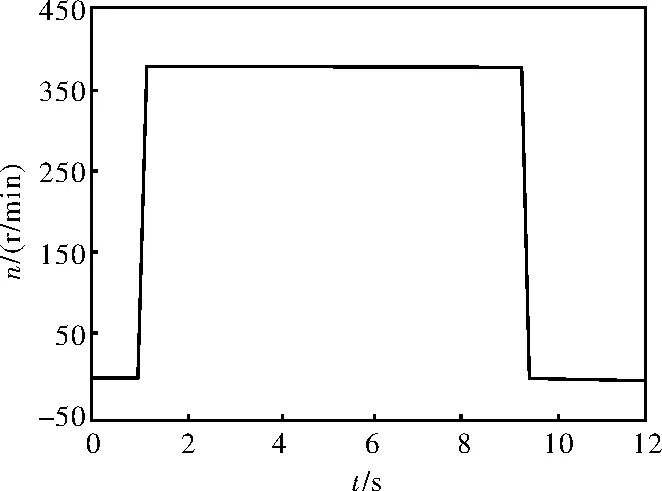
图2 等速运动位置环指令速度曲线

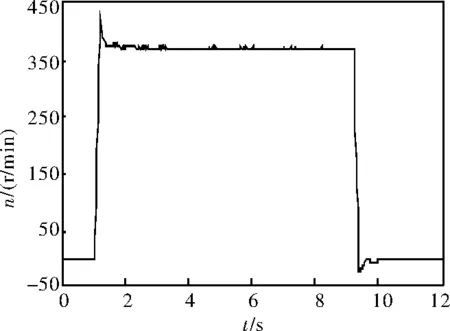
图3 等速运动位置环输出速度曲线

图4 等速运动位置误差曲线

该伺服系统采用速度前馈与位置误差相结合的复合控制方式，在等速跟随运动时，速度前馈指令和位置指令由上位机给出，即使伺服系统出现抖振或跟随不上，指令信号正常给出，该指令不受伺服系统的变化而变化，同时伺服系统只能获取当前指令和过去指令，无法获取超前指令。

从图中可以看出，位置环指令速度曲线没有问题，位置环输出速度曲线在加速段结束时有震荡，位置误差曲线在从最大误差开始减小的过程中存在震荡，减速段与加速段现象类似。图中的加速、减速震荡在负载侧就表现为加速、减速抖振。

由于该伺服系统在生产加工时刚度不足，传动机构弹性较大，导致机械谐振频率变小，同时指令输入信号变化较快，要求伺服系统具有较快的跟随性能，即具有较高的带宽，从而谐振频率进入了伺服系统的带宽内，产生了机械谐振，在负载侧发生了抖振现象。

2 谐振抑制

目前国内外针对伺服系统谐振抑制方法，主要有机械抑制方式和电气抑制方式。

机械抑制方式主要是通过改进连接装置的弹性系数、降低系统的阻尼、减小变速箱的间隙、保证零件生成的加工工艺，使得系统谐振得到抑制。或者将谐振频率提高到系统工作的带宽之外，减小其对系统造成的影响[5]。

电气抑制方式主要是从算法上来抑制谐振。结合控制原理，设计合适的滤波器，将含弹性负载的系统作为一个整体，认为指令中的某次频率谐波成分激发了系统的谐振，而滤波器通过对该频率谐波的幅频衰减，来抵消其引起的幅频突增，达到谐振抑制效果[6-7]。

伺服系统通过伺服电机驱动传动装置运转，伺服系统的谐振频率与系统弹性呈负相关，谐振时的幅值大小与系统弹性呈正相关。由于系统弹性是系统本身固有的属性，一旦系统安装完成，弹性就确定下来，不易进行改变，因此需采用电气抑制方式。

常规的滤波方式中，最主要采用的是双“T”网络陷波滤波器，是通过在给定指令信号之后加入一个陷波滤波器，来滤除引起负载末端谐振的部分，以此来进行谐振抑制[8]。

图5 常规陷波滤波器幅频特性图

常规陷波滤波器幅频特性图如图5所示，通过分析系统的谐振频率，可以得到陷波滤波器需配置的中心谐振频率w0，以及衰减到0.707幅值的两个频率点。

本文在常规陷波滤波器的基础上，根据伺服系统特点及谐振试验数据，考虑到伺服系统的谐振频率具有一定的范围，设计了一种陷波宽度和陷波深度独立可调的陷波滤波器。传递函数为

(1)

式中，w0为陷波频率，k1为陷波深度系数，k2为陷波宽度系数。

陷波宽度代表了陷波滤波器的滤波频率范围，陷波深度代表了陷波滤波器的幅值衰减大小。在进行具体设计时，可独立对深度系数和宽度系数进行调整，以实现更优良的性能。应注意的是，陷波深度系数k1需在0和1之间进行调节，使陷波滤波器具有凹陷的形状，这样才能有效衰减谐振频率点对应的幅值。

通常系统的谐振频率点并不是单一的，而是在一定的频率范围内变化。过窄的陷波宽度将会造成只有中心频点的幅度被抑制而附近的谐振频率没有被抑制的现象，过宽的陷波宽度将会破坏系统的相频特性，在受到干扰时还会破坏稳定性。因此，陷波滤波器的宽度系数k2在设计过程中应兼顾谐振频率的抑制和系统的鲁棒性能。

在设计陷波滤波器的同时，还需要确定伺服系统的谐振频率。一般是通过在线检测误差信号，然后做FFT频谱分析，把时域信号转换为频域信号，再通过频率提取算法获取对应的谐振频率点。

图6 伺服系统谐振抑制框图

伺服系统谐振抑制框图如图6所示。由于该伺服系统为位置跟随系统，因此把陷波滤波器做在位置环。整个伺服系统采用位置环、速度环、电流环三环控制方式，其中位置环采用位置误差和速度前馈控制，用来提高等速运动的快速跟随性能。位置给定与位置反馈的误差值送入位置调节器的同时，也进行FFT频谱分析，从中提取出谐振频率，送至陷波滤波器进行对应频率点的滤波。陷波滤波器输出作为速度环给定，与速度反馈信号一起送至速度调节器，其输出作为电流环给定，与电流反馈通过电流调节器驱动伺服机构按照指令信号运转。

3 试验结果

根据以上分析，设计了一种陷波滤波器，并通过FFT频谱分析计算出伺服系统谐振频率，经过反复调试，确定出陷波滤波器的深度系数k1和宽度系数k2。对伺服系统进行等速试验，试验结果如图7～图9所示。

图7 等速运动位置环指令速度曲线

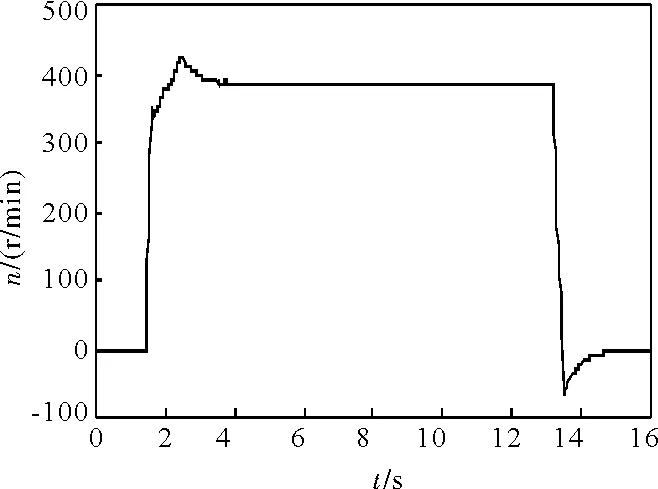
图8 等速运动位置环输出速度曲线(滤波后)

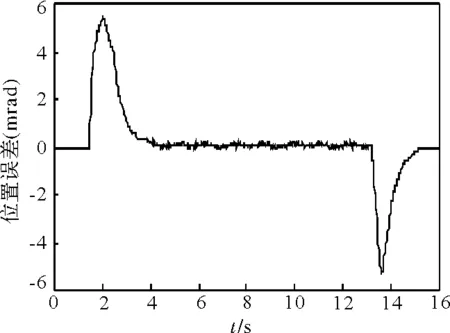
图9 等速运动位置误差曲线(滤波后)

图7、图8、图9分别为等速运动位置环指令速度曲线、滤波后位置环输出速度曲线、滤波后位置误差曲线。图8、图9与图3、图4相比，输出速度达到最大值后，平滑下降到稳定值，没有振荡；位置误差增加时较缓，减小时较平滑，不存在振荡。同时观察伺服系统负载侧，加速、减速过程都较平稳，抖振消失。

本文在位置环采用陷波滤波器后，伺服系统抖振消失，同时引起了加速段和减速段位置误差的增加，这是因为在快速指令信号下作用下滤波器引起了相位滞后所致。但是在伺服系统等速跟随时，加速段和减速段的位置误差不作为考核要求，因此本文所述方法能够满足伺服系统规定的系统指标要求。

4 结 语

本文从现有伺服系统等速运动谐振问题着手，针对等速运动跟随性的特点，设计了一种滤波深度和滤波宽度可调的陷波滤波器来解决加速过程和减速过程发生的抖振问题。通过在线检测误差信号，采用FFT频谱分析，获取伺服系统的谐振频率。最后本文对设计的陷波滤波器进行了等速跟随试验，伺服系统加速和减速过程的抖振消失，试验取得了预期效果，对伺服系统的机械谐振抑制具有一定的参考意义。