基于扰动观测的无轴承电机径向扰动抑制研究

陆 冬，丁 强

(南京工业职业技术学院，南京 210023)

0 引 言

与传统电机相比，无轴承电机由于转子磁悬浮的特点，在许多应用场合具备特殊的优势[1-3]。例如，在超洁净液体的传输驱动领域，无轴承电机转子由于和定子完全分离，很容易封装后置入容器中，实现对液体的离心驱动。此外，无轴承电机不存在机械轴承磨损，在飞轮储能等高速领域同样具备天然的优势。因此无轴承电机作为一种特种电机，在国内外学者间引起了广泛关注[4-5]。

然而也正因为转子的悬浮运行，无轴承电机对转子的装配、传感器的安装精度以及位移检测误差等原因引起的气隙磁密不均匀格外敏感。当转子发生偏心时，不平衡的磁拉力趋向于将转子拉向远离平衡位置。另一方面，气隙磁密不平衡会导致转矩的波动，进一步恶化控制效果，产生振动以及噪音，影响系统的稳定性和安全性。因此径向位移控制的鲁棒性对无轴承电机系统尤为关键，是电机产生稳定转矩的基础[6-8]。这就对位移控制器的性能提出了较高的要求，无轴承电机系统必须要对作用在转子径向上的扰动力具备足够强的抗扰能力。

针对无轴承电机径向扰动导致的稳定性问题，传统控制方案中可通过加强PID参数来加强位移环路的带宽以提高系统的抗扰动能力，但受限于数字控制器的控制周期以及电流环的响应速度，位移环的带宽无法进一步提升，参数过强时反而会带来转子震荡风险。文献[6]通过推导了转子偏心下的数学模型，对悬浮力实现更精确的建模来实现转子位置更平稳的控制，然而，该模型解决了由于模型偏差导致的脉动，但并不能改善外界扰动引起的转子抖动问题。

针对转子径向扰动问题，本文借鉴了传统电机中负载观测方法[7-9]，将转矩负载的观测方法应用于径向扰动的观测中，通过对控制器悬浮力进行补偿，实现无轴承电机径向位移的抗扰动控制。本文首先推导验证了径向扰动观测的可行性，随后通过仿真和理论分析验证了观测器对位移控制的改善效果。最后通过实验验证了该算法的有效性。

1 拓扑结构及数学模型

集中式绕组的表贴式无轴承永磁电机典型拓扑如图1所示，该结构电机由六个定子齿和一对极的表贴式转子组成，六个线圈绕制在各自的定子齿上。

根据无轴承电机悬浮的理论[10]，六个绕组内的电流需要由转矩电流和悬浮电流两种分量叠加组成，其形式可以写为

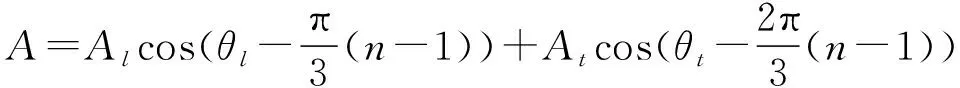
(1)

图1 表贴式无轴承永磁电机拓扑结构

式中，Al为悬浮电流幅值，θl为悬浮电流相位，At为转矩电流幅值，θt为转矩电流相位。推导该结构电机的径向悬浮力的数学模型的表达式为

(2)

其中的系数为

(3)

(4)

式中，μ0为空气磁导率，r为转子半径，h为转子轴向长度，leg为气隙长度，α为齿宽弧度。θr转矩电流相位。APM为永磁磁势幅值，θr为转子机械转角，lpx、lpy分别为转子在x和y方向上的偏心距离。

式(2)可以看出，转子径向力由两部分组成。第一项是由绕组电流产生，由于永磁磁势的幅值远大于转矩电流产生的磁势，即APM≫At，因此悬浮电流的幅值和相位对悬浮力的产生起主要作用，转矩电流对悬浮力可看作是扰动。第二项为不平衡磁拉力，由转子偏心产生。一般情况下，由于转子偏心量较小，线性化后可以近似认为不平衡磁拉力正比于转子的偏心位移，即系数kxx和kyy近似为常数。

2 扰动观测器模型

从上节的悬浮力数学模型中可以注意到，转矩电流和悬浮电流的作用效果并非完全解耦的，当电机旋转维度施加重载时，绕组内的转矩电流会在径向上产生扰动作用，给电机的径向稳定造成一定的影响。除此之外，模型的非线性、负载振动等因素都会在转子径向产生不确定的扰动，影响转子的稳定悬浮。针对此问题，本文引入了扰动观测器以降低径向扰动的影响，提高悬浮性能。

观测器的核心思想为在控制系统中重构一个与真实被控对象等价的系统，并将控制量作用于该系统，当该系统的输出与真实系统相同时，便可将观测的状态量当做是真实系统的状态量实现状态反馈。

无轴承电机转子的机械运动方程可写为

(5)

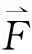
选取转子位移 、转子速度 和扰动力 作为系统的状态量x:

(6)

可将式(5)的运动方程写为如下所示的状态形式:

(7)

式中各矩阵的表达式如下:

(8)

(9)

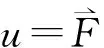
(10)

式(7)所示的状态方程形式展开后如下:

(11)

系统的输出方程为

y=Cx

(12)

(13)

式中,“^”表示估计量，将观测器的输出与系统的实际输出作差后，通过矩阵H反馈至估计量的微分状态，可使观测器的输出与实际系统输出间的误差收敛至零。反馈矩阵H的形式为H=[h1h2h3]T，h1、h2、h3为待定系数。引入了状态观测器后的系统结构框图如图2所示。

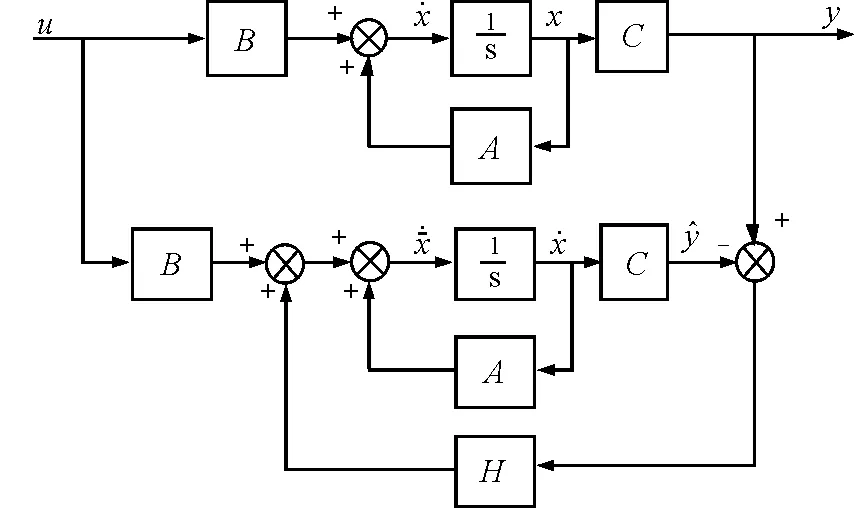
图2 状态观测器结构框图

由此可以得到引入了状态反馈后的系统状态方程:

(14)

根据式(14)可以设计出扰动观测器的结构框图如图3所示。

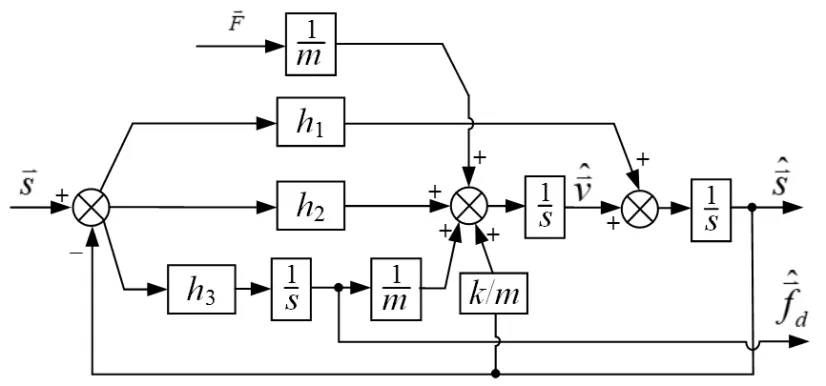
图3 扰动观测器框图

观测器的特征方程为

(15)

若状态观测器的目标极点为p1，p2，p3。

det[sI-(A-HC)]=(s-p1)(s-p2)(s-p3)

(16)

通过待定系数法可以求得

(17)

状态观测器的误差收敛的条件是全部期望极点具有负实部，即极点应该位于s平面的左半平面部分。通过合理设置观测器的极点，可以实现其输出对系统真实状态量的跟踪。

实现扰动观测后，需要将观测器输出的扰动量作为补偿量提供给PID控制器，以抵消真实扰动给位移环带来的扰动。优化后的抗扰动控制框图如图4所示。

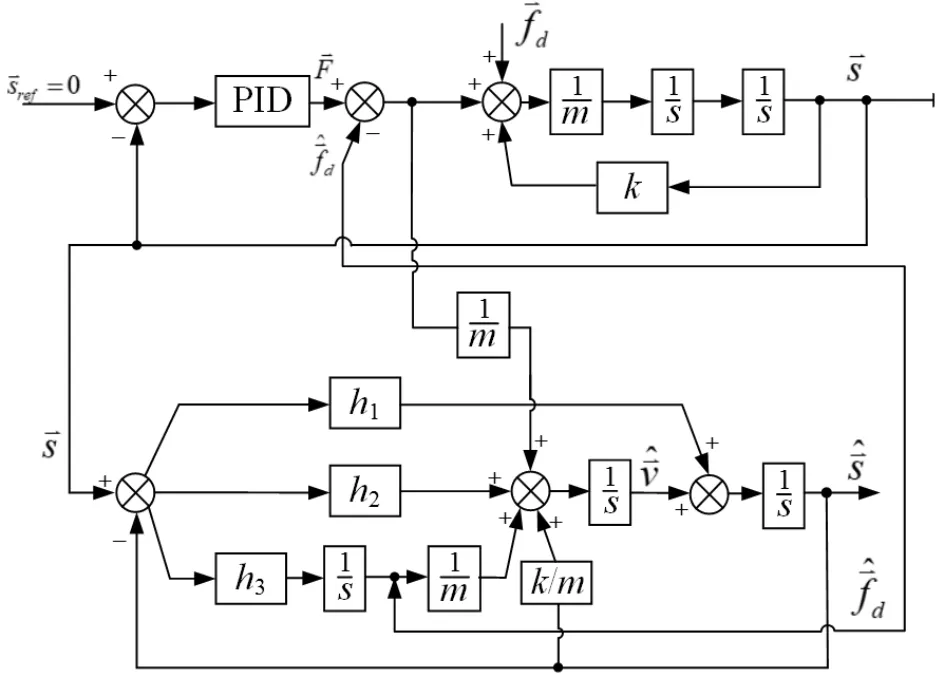
图4 无轴承电机抗扰动控制框图

3 仿真及带宽分析

为验证扰动观测器的性能，在Matlab/Simulink中搭建仿真模型，仿真所用的参数如下:转子质量0.2 kg，径向位移刚度30 N/mm，忽略了电机实际控制过程中电流环的延迟影响。

图5 阶跃作用力下的径向位移响应

图5对比了径向阶跃负载情况下，传统PID控制和加入了扰动观测后的径向位移响应波形，主环路所用的PID参数相同。从图5(b)中可以看到，通过合理的零极点配置，观测器对阶跃负载有着较好的跟踪效果，在3.5 ms时间内观测器输出收敛到真实绕动力附近。采用传统PID控制时，在阶跃的径向扰动作用下，主要依靠积分环节的调节产生径向力与扰动平衡，其调节速度较慢，因此位移的恢复时间较长。加入了扰动观测后，位移环的动态性能被大大改善，阶跃扰动下的位置偏移从50 μm降低至13 μm，恢复稳态的时间从约40 ms缩短至18 ms。

由于电机转子是一旋转的系统，径向的扰动在更多时候以交变的形式呈现。例如，当转子质心与几何中心不重合时，会在径向形成扰动力。这些扰动均可看做是径向的负载。图6仿真验证了在正弦交变径向力作用下，传统PID控制和加入了扰动观测补偿的效果对比，径向扰动力的幅值为5 N，频率为50 Hz。可以看到，由于负载观测器的带宽足够强，可以对该频段的负载变化实现较好的跟踪。将观测的负载引入主环路进行补偿后，转子径向位移的脉动被有效降低，径向的波动从50 μm降低至11 μm。

图6 正弦径向力下的位移响应

通过带宽分析可以验证扰动观测器对位移控制环路的改善效果，根据图4展示的控制框图，可以推导出加入扰动观测器前后，实际位移与给定位移之间的传递函数H1(s)，加入扰动观测前后传递函数均为

(18)

这表明加入扰动观测并不会影响主环路的传递函数，进一步推导位移和扰动力之间的传递函数，在不加入扰动观测时，传递函数表达式为

(19)

加入扰动观测后，传递函数可以写为

(20)

其中，a1=m；a2=mh1；a3=mh2-k；b1=m2；b2=m2h1+mkD；b3=mkP-2mk+h2m2+mh1kD；b4=mh3-kkD+mkI-mkh1+mh2kD+mh1kP；b5=h3kD-kkP+k2-h2mk+mh2kP+mh1kI；b6=mh2kI-kkI+kPh3-kh3；b7=kIh3；

将仿真中用的参数代入式(19)和式(20)中绘制波特图，如图7所示，对比优化前后的幅频曲线可以看到，加入了扰动观测后，低频段的信号从-140dB衰减到了-205dB左右，这表明低频的扰动信号得到了更有效的抑制。但在高频段，幅频曲线与优化前基本重合，这表明负载观测器对高频段的扰动基本不起作用。因此事先可以根据扰动的频段范围设计扰动观测器的零极点，以便获得更优的抗扰动效果。

图7 位移与扰动间传递函数波特图

4 实验验证

本文通过实验验证了扰动观测补偿的优化效果。图8验证了电机在900 r/min时的径向位移波形，在开启扰动观测前，采用传统PID控制，由于转子质心与几何中心不重合，转子在径向受到绕动力的影响，位移波动约为±100 μm，波动的频率与转速同频。开启了负载观测补偿后，位移波动迅速减小至原先的1/4，波动仅为±25 μm，改善效果明显。

图8 900 r/min时扰动观测后的位移波形

图9验证了转子在静止悬浮时，径向受到一冲击扰动时的位移波形。第一次冲击扰动时采用了传统PID控制，在该扰动下，y方向位移的波动达到约100 μm，而开启负载观测补偿后，同样的冲击扰动仅造成不到50 μm的波动。

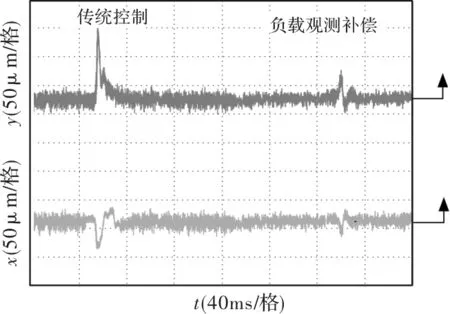
图9 径向冲击作用下的位移波形

5 结 语

本文针对无轴承电机径向扰动的问题，通过状态观测的方法来改善位移控制器的鲁棒性。本文推导构造了扰动观测器，并给出了观测器的收敛条件。随后仿真验证了优化后的抗扰动性能，通过分析位移与扰动力间的幅频响应曲线可以进一步从理论验证对径向扰动的抑制效果。最后文章通过实验验证了扰动观测的有效性，优化后，在冲击以及交变的扰动下，位移波动均得到有效的抑制，控制的稳定性能得到了提高。